1 Introduction

In the past few years, neural networks have been widely studied and applied in various fields such as load frequency control in pattern recognition, static image processing, associative memories, mechanics of structures and materials, optimization and other scientific areas (see [1–16]). The BAM neural network model is an extension of the unidirectional auto-associator of Hopfield. A BAM neural network is composed of neurons arranged in two layers: X- and Y-layers. The neurons in one layer are fully interconnected to the neurons in the other layer, while there are no interconnection among neurons in the same layer [17]. The BAM neural networks have potential applications in many fields such as signal processing, artificial intelligence and so on. In addition, time delays are inevitable in many biological and artificial neural networks such as signal transmission delay, propagation and signal processing delay. It is well known that the existence of time delays is the source of oscillation and instability in neural networks which can change the dynamic characters of neural networks dramatically. The stability of neural networks has drawn particular research interest. The stability of BAM neural networks also has been widely studied, and a lot of results have been reported (see [18, 19] and the references cited therein).

In relatively large-scale neural networks, the state components of the neural network model are unknown or not available for direct measurement, normally only partial information about the neuron states is available in the network outputs. In order to make use of the neural networks in practice, it is important and necessary to estimate the neuron states through available measurements. Recently, the state estimation problem for neural networks has received increasing research interest (see [20–26]). The state estimation problem for delayed neural networks has been proposed in [20]. Mou et al. [21] studied state estimation for discrete-time neural networks with time-varying delays. A sufficient condition was derived for the design of the state estimator to guarantee the global exponential stability of the error system. The problem of state estimation for discrete-time delayed neural networks with fractional uncertainties and sensor saturations was studied in [22]. In [26], the state estimation problem for a new class of discrete-time neural networks with Markovian jumping parameters as well as mode-dependent mixed time-delays is studied. New techniques are developed to deal with the mixed time-delays in the discrete-time setting, and a novel Lyapunov-Krasovskii functional is put forward to reflect the mode-dependent time-delays. Sufficient conditions are established in terms of linear matrix inequalities (LMIs) that guarantee the existence of the state estimators.

However, only very little attention has been paid to state estimation for BAM neural networks with time-varying delay. The robust delay-dependent state estimation problem for a class of discrete-time BAM neural networks with time-varying delays is considered in [27]. By using the Lyapunov-Krasovskii functional together with linear matrix inequality (LMI) approach, a new set of sufficient conditions is derived for the existence of state estimator such that the error state system is asymptotically stable. The problem of state estimator of BAM neural network with leakage delays is studied in [28]. A sufficient condition is established to ensure that the error system was globally asymptotically stable. It should be pointed out that only the global asymptotical stability of the error system was discussed in [27, 28]. To the best of our knowledge, the exponential stability of the error system for the discrete-time BAM neural networks with time-varying delay has not been fully addressed yet. Motivated by this consideration, in this paper we aim to establish some new sufficient conditions for the existence of state estimations which guarantee the error system for the discrete-time BAM neural networks with time-varying delays to be globally exponentially stable. These conditions are expressed in the form of LMIs.

The rest of this paper is organized as follows. In Section 2, some notations and lemmas, which will be used in this paper, are given. In Section 3, based on utilizing both the delay partitioning method and the reciprocally convex approach, we construct a novel Lyapunov-Krasovskii functional, and a new set of sufficient conditions are derived for the global exponential stability of the error system. In Section 4, an illustrative example is provided to demonstrate the effectiveness of the proposed result.

2 Problem formulation and preliminaries

For the sake of convenience, we introduce some notations firstly. ∗ denotes the symmetric term in a symmetric matrix. For an arbitrary matrix A, \(A^{T}\) stands for the transpose of A. \(A^{-1}\) denotes the inverse of A. \(R^{n\times n}\) denotes the \(n\times n\)-dimensional Euclidean space. If A is a symmetric matrix, \(A>0\) (\(A\geq0\)) means that A is positive definite (positive semidefinite). Similarly, \(A<0\) (\(A\leq0\)) means that A is negative definite (negative semidefinite). \(\lambda_{m}(A)\), \(\lambda_{M}(A)\) denote the minimum and maximum eigenvalues of a square matrix A, respectively. \(\|A\|=\sqrt{\lambda_{M}(A^{T}A)}\).

In this paper, we consider the following class of discrete-time BAM neural networks with time-varying delays:

$$ \begin{aligned} &x(k+1)=Ax(k)+Cf\bigl(y(k)\bigr)+Ef\bigl(y \bigl(k-d(k)\bigr)\bigr)+I, \\ &y(k+1)=By(k)+Dg\bigl(x(k)\bigr)+Wg\bigl(x\bigl(k-h(k)\bigr)\bigr)+J \end{aligned} $$
(1)

for \(k =1,2,\ldots,n\), where \(x(k)=(x_{1}(k),x_{2}(k),\ldots,x_{n}(k))^{T}\), \(y(k)=(y_{1}(k),y_{2}(k),\ldots,y_{n}(k))^{T}\) are the neuron state vectors; \(A=\operatorname{diag}(a_{1},a_{2},\ldots,a_{n})\), and \(B=\operatorname{diag} (b_{1},b_{2},\ldots,b_{n})\) are the state feedback coefficient matrices, \(|a_{i}|<1\), \(|b_{i}|<1\), \(i=1,2,\ldots,n\); \(C=[c_{ij}]_{n\times n}\), \(D=[d_{ij}]_{n\times n}\) are the connection weight matrices; \(E=[e_{ij}]_{n\times n}\), and \(W=[w_{ij}]_{n\times n}\) are the delayed connection weight matrices; \(f(y(k))=(f_{1}(y_{1}(k)), f_{2}(y_{2}(k)),\ldots,f_{n}(y_{n}(k)))^{T}\), and \(g(x(k))=(g_{1}(x_{1}(k)), g_{2}(x_{2}(k)),\ldots,g_{n}(x_{n}(k)))^{T}\) denote the neuron activation functions; \(h(k)\) and \(d(k)\) denote the time-varying delays satisfying \(0\leq h_{m} \leq h(k)\leq h_{M}\), \(0 \leq d_{m} \leq d(k)\leq d_{M}\), where \(h_{m}\), \(h_{M}\), \(d_{m}\), \(d_{M}\) are known positive integers; I and J denote the external constant inputs from outside network.

Throughout this paper, we make the following assumptions.

Assumption 1

There exist constants \(F_{i}^{-}\), \(F_{i}^{+}\), \(G_{i}^{-}\) and \(G_{i}^{+}\) such that

$$\begin{aligned}& G_{i}^{-}\leq\frac{g_{i}(x)-g_{i}(y)}{x-y}\leq G_{i}^{+}\quad \mbox{for all }x,y\in R, x\neq y,i=1,2,\ldots,n, \\& F_{i}^{-}\leq\frac{f_{i}(x)-f_{i}(y)}{x-y}\leq F_{i}^{+}\quad \mbox{for all }x,y\in R, x\neq y,i=1,2,\ldots,n, \\& f_{i}(0)=g_{i}(0)=0. \end{aligned}$$

Remark 1

In Assumption 1, the constants \(F_{i}^{-}\), \(F_{i}^{+}\), \(G_{i}^{-}\) and \(G_{i}^{+}\) are allowed to be positive, negative, or zero. So the activation functions in this paper are more general than nonnegative sigmoidal functions used in [29, 30]. The stability condition developed in this paper is less restrictive than that in [29, 30].

For presentation convenience, we denote

$$\begin{aligned}& F_{1}=\operatorname{diag}\bigl(F_{1}^{-}F_{1}^{+},F_{2}^{-}F_{2}^{+}, \ldots,F_{n}^{-}F_{n}^{+}\bigr),\quad F_{2}= \operatorname{diag}\biggl(\frac{F_{1}^{-}+F_{1}^{+}}{2},\frac{F_{2}^{-}+F_{2}^{+}}{2},\ldots, \frac {F_{n}^{-}+F_{n}^{+}}{2}\biggr), \\& G_{1}=\operatorname{diag}\bigl(G_{1}^{-}G_{1}^{+},G_{2}^{-}G_{2}^{+}, \ldots,G_{n}^{-}G_{n}^{+}\bigr),\quad G_{2}= \operatorname{diag}\biggl(\frac{G_{1}^{-}+G_{1}^{+}}{2},\frac{G_{2}^{-}+G_{2}^{+}}{2},\ldots, \frac {G_{n}^{-}+G_{n}^{+}}{2}\biggr). \end{aligned}$$

For some relatively large scale neural networks, it is difficult to achieve all the information about the network computer. So, one often needs to utilize the estimated neuron states to achieve certain design objectives. We assume that the network measurements are as follows:

$$ \begin{aligned} &z_{x}(k)=M_{1}x(k), \\ &z_{y}(k)=M_{2}y(k), \end{aligned} $$
(2)

where \(z_{x}(k)\), \(z_{y}(k)\) are the measurement outputs, and \(M_{1}\), \(M_{2}\) are the known constant matrices with appropriate dimensions. Therefore, the full-order state estimator is of the form

$$\begin{aligned}& \begin{aligned} \widehat{x}(k+1)={}&A\widehat{x}(k)+Cf\bigl( \widehat {y}(k)\bigr)+Ef\bigl(\widehat{y}\bigl(k-d(k)\bigr)\bigr)+I \\ &{}+K_{1}\bigl(z_{x}(k)-M_{1}\widehat{x}(k) \bigr), \\ \widehat{y}(k+1)={}&B\widehat {y}(k)+Dg\bigl(\widehat{x}(k)\bigr)+Wg\bigl( \widehat{x}\bigl(k-h(k)\bigr)\bigr)+J \\ &{}+K_{2}\bigl(z_{y}(k)-M_{2}\widehat{y}(k) \bigr), \end{aligned} \end{aligned}$$
(3)

where \(\widehat{x}(k)\), \(\widehat{y}(k)\) are the estimations of \(x(k)\), \(y(k)\), respectively, \(K_{1}\), \(K_{2}\) are the gain matrices of the estimator to be designed later.

Let the estimation error be \(e_{1}(k)=x(k)-\widehat{x}(k)\) and \(e_{2}(k)=y(k)-\widehat{y}(k)\). Then the error system can be written as

$$ \begin{aligned} e_{1}(k+1)={}&(A-K_{1}M_{1})e_{1}(k)+C \bigl(f\bigl(y(k)\bigr)-f\bigl(\widehat {y}(k)\bigr)\bigr) \\ &{}+E\bigl(f\bigl(y\bigl(k-d(k)\bigr)\bigr)-f\bigl(\widehat{y}\bigl(k-d(k)\bigr)\bigr) \bigr), \\ e_{2}(k+1)={}&(B-K_{2}M_{2})e_{2}(k)+D \bigl(g\bigl(x(k)\bigr)-g\bigl(\widehat{x}(k)\bigr)\bigr) \\ &{}+W\bigl(g\bigl(x\bigl(k-h(k)\bigr)\bigr)-g\bigl(\widehat{x}\bigl(k-h(k)\bigr)\bigr) \bigr). \end{aligned} $$
(4)

By defining \(\xi_{1}(k)=f(y(k))-f(\widehat{y}(k))\), \(\xi _{1}(k-d(k))=f(y(k-d(k)))-f(\widehat{y}(k-d(k)))\), \(\xi _{2}(k)=g(x(k))-g(\widehat{x}(k))\), \(\xi_{2}(k-h(k))=g(x(k-h(k)))-g(\widehat{x}(k-h(k)))\), system (4) can be rewritten as

$$ \begin{aligned} &e_{1}(k+1)=(A-K_{1}M_{1})e_{1}(k)+C \xi_{1}(k)+E\xi_{1}\bigl(k-d(k)\bigr), \\ &e_{2}(k+1)=(B-K_{2}M_{2})e_{2}(k)+D \xi_{2}(k)+W\xi_{2}\bigl(k-h(k)\bigr). \end{aligned} $$
(5)

Before presenting the main results of the paper, we need the following definition and lemmas.

Definition 1

The error system (5) is said to be globally exponentially stable if there exist two scalars \(\lambda>0 \) and \(r>1\) such that

$$ \bigl\| e_{1}(k)\bigr\| ^{2}+\bigl\| e_{2}(k) \bigr\| ^{2}\leq\lambda r^{-k}\Bigl(\sup_{-h_{M}\leq s\leq0}\bigl\| e_{1}(s)\bigr\| ^{2}+\sup_{-d_{M}\leq s\leq0}\bigl\| e_{2}(s)\bigr\| ^{2}\Bigr). $$
(6)

Lemma 1

[31]

For any positive definite matrix \(J\in R^{n\times n}\), two positive integers r and \(r_{0}\) satisfying \(r\geq r_{0}\geq1\), and vector function \(x(i)\in R^{n}\), one has

$$\begin{aligned} \Biggl(\sum_{i=r_{0}}^{r}x(i) \Biggr)^{T}J\Biggl(\sum_{i=r_{0}}^{r}x(i) \Biggr)\leq(r-r_{0}+1)\sum_{i=r_{0}}^{r}x^{T}(i)Jx(i). \end{aligned}$$

Lemma 2

[32]

Let \(f_{1}, f_{2}, \ldots, f_{N}: R^{m}\mapsto R\) have positive values in an open subset D of \(R^{m}\). Then the reciprocally convex combination of \(f_{i}\) over D satisfies

$$\begin{aligned} &\min_{\{\alpha_{i}|\alpha_{i}>0,\sum_{i}\alpha_{i}=1\}}\sum\frac {1}{\alpha_{i}}f_{i}(k)= \sum_{i}f_{i}(k)+\max _{g_{i,j}(k)}\sum_{i\neq j}g_{i,j}(k) \\ &\textit{subject to} \\ & \Biggl\{ g_{i,j}:R^{m} \mapsto R, g_{j,i}(k) \triangleq g_{i,j}(k), \begin{bmatrix} f_{i}(k) & g_{i,j}(k) \\ g_{i,j}(k) & f_{j}(k) \end{bmatrix} \geq0 \Biggr\} . \end{aligned}$$

3 Main results

In this section, we construct a novel Lyapunov-Krasovskii functional together with free-weighting matrix technique. A delay-dependent condition is derived to estimate the neuron state through available output measurements such that the resulting error system (5) is globally exponentially stable.

Theorem 1

Under Assumption  1, the error state system (5) is globally exponentially stable if there exist symmetric positive define matrices \(P_{1}>0\), \(P_{2}>0\), \(Q_{i}>0\), \(R_{i}>0\) (\(i=1,2,3,4,5,6\)), positive diagonal matrices \(U_{j}>0\) (\(j=1,2,3,4\)), and matrices \(L_{1}\), \(L_{2}\), \(S_{1}\), \(S_{2}\), X, Y of appropriate dimensions such that the following LMIs hold:

$$\begin{aligned}& \begin{bmatrix} R_{i}&S_{j}\\ \star&R_{i} \end{bmatrix} \geq0 \quad(i=5,6; j=1,2), \end{aligned}$$
(7)
$$\begin{aligned}& \Phi=[\Phi_{ij}]_{14\times14} < 0, \end{aligned}$$
(8)

where \(\Phi_{1,1}=P_{1}+h_{m}^{2}R_{1}+h_{M}^{2}R_{3}+(h_{M}-h_{m})^{2}R_{5}+L_{1}^{T}+L_{1}\), \(\Phi_{1,2}=-h_{m}^{2}R_{1}-h_{M}^{2}R_{3}-(h_{M}-h_{m})^{2}R_{5}-L_{1}A+XM_{1}\), \(\Phi _{1,6}=-L_{1}C\), \(\Phi_{1,7}=-L_{1}E\), \(\Phi _{2,2}=-P_{1}+(h_{M}-h_{m}+1)Q_{1}+Q_{3}+Q_{5}+(h_{m}^{2}-1)R_{1} +(h_{M}^{2}-1)R_{3}+(h_{M}-h_{m})^{2}R_{5}-G_{1}U_{3}\), \(\Phi_{2,4}=R_{1}\), \(\Phi_{2,5}=R_{3}\), \(\Phi_{2,13}=G_{2}U_{3}\), \(\Phi _{3,3}=-Q_{1}-2R_{5}+S_{1}^{T}+S_{1}-G_{1}U_{4}\), \(\Phi_{3,4}=R_{5}^{T}-S_{1}\), \(\Phi_{3,5}=-S_{1}^{T}+R_{5}\), \(\Phi_{3,14}=G_{2}U_{4}\), \(\Phi _{4,4}=-Q_{3}-R_{1}-R_{5}\), \(\Phi_{4,5}=S_{1}^{T}\), \(\Phi_{5,5}=-Q_{5}-R_{3}-R_{5}\), \(\Phi_{6,6}=-U_{1}\), \(\Phi_{6,9}=F_{2}U_{1}\), \(\Phi_{7,7}=-U_{2}\), \(\Phi_{7,10}=F_{2}U_{2}\), \(\Phi_{8,8}=P_{2}+d_{m}^{2}R_{2}+d_{M}^{2}R_{4}+(d_{M}-d_{m})^{2}R_{6}+L_{2}^{T}+L_{2}\), \(\Phi_{8,9}=-d_{m}^{2}R_{2}-d_{M}^{2}R_{4}-(d_{M}-d_{m})^{2}R_{6}-L_{2}A+YM_{2}\), \(\Phi_{8,13}=-L_{2}D\), \(\Phi_{8,14}=-L_{2}W\), \(\Phi_{9,9}=-P_{2}+(d_{M}-d_{m}+1)Q_{2}+Q_{4}+Q_{6}+(d_{m}^{2}-1)R_{2} +(d_{M}^{2}-1)R_{4}+(d_{M}-d_{m})^{2}R_{6}-F_{1}U_{1}\), \(\Phi_{9,11}=R_{2}\), \(\Phi_{9,12}=R_{4}\), \(\Phi_{10,10}=-Q_{2}-2R_{6}+S_{2}^{T}+S_{2}-F_{1}U_{2}\), \(\Phi_{10,11}=R_{6}^{T}-S_{2}\), \(\Phi_{10,12}=-S_{2}^{T}+R_{6}\), \(\Phi_{11,11}=-Q_{4}-R_{2}-R_{6}\), \(\Phi _{11,12}=S_{2}^{T}\), \(\Phi_{12,12}=-Q_{6}-R_{4}-R_{6}\), \(\Phi_{13,13}=-U_{3}\), \(\Phi_{14,14}=-U_{4}\), and other terms are zeros. Then the gain matrices \(K_{1}\), \(K_{2}\) of state estimator are given by \(K_{1}=L_{1}^{-1}X\), \(K_{2}=L_{2}^{-1}Y\).

Proof

Consider the LKFs for the error state system (5) as follows:

$$ V(k)=\sum_{i=1}^{8}V_{i}(k), $$
(9)

where

$$\begin{aligned}& V_{1}(k)=e_{1}^{T}(k)P_{1}e_{1}(k)+e_{2}^{T}(k)P_{2}e_{2}(k), \\& V_{2}(k)=\sum_{i=k-h(k)}^{k-1}e_{1}^{T}(i)Q_{1}e_{1}(i)+ \sum_{i=k-d(k)}^{k-1}e_{2}^{T}(i)Q_{2}e_{2}(i), \\& V_{3}(k)=\sum_{i=k-h_{m}}^{k-1}e_{1}^{T}(i)Q_{3}e_{1}(i)+ \sum_{i=k-d_{m}}^{k-1}e_{2}^{T}(i)Q_{4}e_{2}(i), \\& V_{4}(k)=\sum_{i=k-h_{M}}^{k-1}e_{1}^{T}(i)Q_{5}e_{1}(i)+ \sum_{i=k-d_{M}}^{k-1}e_{2}^{T}(i)Q_{6}e_{2}(i), \\& V_{5}(k)=\sum_{i=-h_{M}+1}^{-h_{m}}\sum _{j=k+i}^{k-1}e_{1}^{T}(j)Q_{1}e_{1}(j)+ \sum_{i=-d_{M}+1}^{-d_{m}}\sum _{j=k+i}^{k-1}e_{2}^{T}(j)Q_{2}e_{2}(j), \\& V_{6}(k)=h_{m}\sum_{i=-h_{m}}^{-1} \sum_{j=k+i}^{k-1}\eta _{1}^{T}(j)R_{1} \eta_{1}(j) +d_{m}\sum_{i=-d_{m}}^{-1} \sum_{j=k+i}^{k-1}\eta _{2}^{T}(j)R_{2} \eta_{2}(j), \\& V_{7}(k)=h_{M}\sum_{i=-h_{M}}^{-1} \sum_{j=k+i}^{k-1}\eta _{1}^{T}(j)R_{3} \eta_{1}(j) +d_{M}\sum_{i=-d_{M}}^{-1} \sum_{j=k+i}^{k-1}\eta _{2}^{T}(j)R_{4} \eta_{2}(j), \\& V_{8}(k)=(h_{M}-h_{m})\sum _{i=-h_{M}}^{-h_{m}-1}\sum_{j=k+i}^{k-1} \eta_{1}^{T}(j)R_{5}\eta_{1}(j) +(d_{M}-d_{m})\sum_{i=-d_{M}}^{-d_{m}-1} \sum_{j=k+i}^{k-1}\eta _{2}^{T}(j)R_{6} \eta_{2}(j), \end{aligned}$$

where \(\eta_{1}(k)=e_{1}(k+1)-e_{1}(k)\), and \(\eta_{2}(k)=e_{2}(k+1)-e_{2}(k)\). We define forward difference of \(V_{i}(k)\) as \(\Delta V_{i}(k) =V_{i}(k+1)-V_{i}(k)\). Then the forward difference of \(V_{i}(k)\) can be derived as follows:

$$\begin{aligned} \Delta V_{1}(k) =&e_{1}^{T}(k+1)P_{1}e_{1}(k+1)-e_{1}^{T}(k)P_{1}e_{1}(k) \\ &{}+e_{2}^{T}(k+1)P_{2}e_{2}(k+1)-e_{2}^{T}(k)P_{2}e_{2}(k), \end{aligned}$$
(10)
$$\begin{aligned} \Delta V_{2}(k) =&\sum_{i=k+1-h(k+1)}^{k}e_{1}^{T}(i)Q_{1}e_{1}(i)- \sum_{i=k-h(k)}^{k-1}e_{1}^{T}(i)Q_{1}e_{1}(i) \\ &{}+\sum_{i=k+1-d(k+1)}^{k}e_{2}^{T}(i)Q_{2}e_{2}(i)- \sum_{i=k-d(k)}^{k-1}e_{2}^{T}(i)Q_{2}e_{2}(i) \\ =& e_{1}^{T}(k)Q_{1}e_{1}(k)-e_{1}^{T} \bigl(k-h(k)\bigr)Q_{1}e_{1}\bigl(k-h(k)\bigr) \\ &{}+\sum_{i=k+1-h(k+1)}^{k-1}e_{1}^{T}(i)Q_{1}e_{1}(i)- \sum_{i=k+1-h(k)}^{k-1}e_{1}^{T}(i)Q_{1}e_{1}(i) \\ &{}+e_{2}^{T}(k)Q_{2}e_{2}(k)-e_{2}^{T} \bigl(k-d(k)\bigr)Q_{2}e_{2}\bigl(k-d(k)\bigr) \\ &{}+\sum_{i=k+1-d(k+1)}^{k-1}e_{2}^{T}(i)Q_{2}e_{2}(i)- \sum_{i=k+1-d(k)}^{k-1}e_{2}^{T}(i)Q_{2}e_{2}(i) \\ \leq& e_{1}^{T}(k)Q_{1}e_{1}(k)-e_{1}^{T} \bigl(k-h(k)\bigr)Q_{1}e_{1}\bigl(k-h(k)\bigr) \\ &{}+\sum_{i=k+1-h(k+1)}^{k-h_{m}}e_{1}^{T}(i)Q_{1}e_{1}(i)+ \sum_{i=k+1-h_{m}}^{k-1}e_{1}^{T}(i)Q_{1}e_{1}(i) \\ &{}-\sum_{i=k+1-h_{m}}^{k-1}e_{1}^{T}(i)Q_{1}e_{1}(i)+e_{2}^{T}(k)Q_{2}e_{2}(k) \\ &{}-e_{2}^{T}\bigl(k-d(k)\bigr)Q_{2}e_{2} \bigl(k-d(k)\bigr)+\sum_{i=k+1-d(k+1)}^{k-d_{m}}e_{2}^{T}(i)Q_{2}e_{2}(i) \\ &{}+\sum_{i=k+1-d_{m}}^{k-1}e_{2}^{T}(i)Q_{2}e_{2}(i)- \sum_{i=k+1-d_{m}}^{k-1}e_{2}^{T}(i)Q_{2}e_{2}(i) \\ \leq&e_{1}^{T}(k)Q_{1}e_{1}(k)-e_{1}^{T} \bigl(k-h(k)\bigr)Q_{1}e_{1}\bigl(k-h(k)\bigr) \\ &{} +\sum_{i=k+1-h_{M}}^{k-h_{m}}e_{1}^{T}(i)Q_{1}e_{1}(i)+e_{2}^{T}(k)Q_{2}e_{2}(k) \\ &{}-e_{2}^{T}\bigl(k-d(k)\bigr)Q_{2}e_{2} \bigl(k-d(k)\bigr)+\sum_{i=k+1-d_{M}}^{k-d_{m}}e_{2}^{T}(i)Q_{2}e_{2}(i), \end{aligned}$$
(11)
$$\begin{aligned} \Delta V_{3}(k) =&e_{1}^{T}(k)Q_{3}e_{1}(k)-e_{1}^{T}(k-h_{m})Q_{3}e_{1}(k-h_{m}) \\ &{}+e_{2}^{T}(k)Q_{4}e_{2}(k)-e_{2}^{T}(k-d_{m})Q_{4}e_{2}(k-d_{m}), \end{aligned}$$
(12)
$$\begin{aligned} \Delta V_{4}(k) =&e_{1}^{T}(k)Q_{5}e_{1}(k)-e_{1}^{T}(k-h_{M})Q_{5}e_{1}(k-h_{M}) \\ &{}+e_{2}^{T}(k)Q_{6}e_{2}(k)-e_{2}^{T}(k-d_{M})Q_{6}e_{2}(k-d_{M}), \end{aligned}$$
(13)
$$\begin{aligned} \Delta V_{5}(k) =&(h_{M}-h_{m})e_{1}^{T}(k)Q_{1}e_{1}(k)- \sum_{i=k+1-h_{M}}^{k-h_{m}}e_{1}^{T}(i)Q_{1}e_{1}(i) \\ &{}+(d_{M}-d_{m})e_{2}^{T}(k)Q_{2}e_{2}(k)- \sum_{i=k+1-d_{M}}^{k-d_{m}}e_{2}^{T}(i)Q_{2}e_{2}(i). \end{aligned}$$
(14)

From Lemma 1, we can obtain

$$\begin{aligned} \Delta V_{6}(k) =&h_{m}^{2} \eta_{1}^{T}(k)R_{1}\eta _{1}(k)+d_{m}^{2} \eta_{2}^{T}(k)R_{2}\eta_{2}(k) \\ &{}-h_{m}\sum_{i=k-h_{m}}^{k-1} \eta_{1}^{T}(i)R_{1}\eta_{1}(i) \\ &{}-d_{m}\sum_{i=k-d_{m}}^{k-1} \eta_{2}^{T}(i)R_{2}\eta_{2}(i) \\ \leq&h_{m}^{2}\eta_{1}^{T}(k)R_{1} \eta_{1}(k)+d_{m}^{2}\eta_{2}^{T}(k)R_{2} \eta_{2}(k) \\ &{}-\bigl(e_{1}(k)-e_{1}(k-h_{m}) \bigr)^{T}R_{1}\bigl(e_{1}(k)-e_{1}(k-h_{m}) \bigr) \\ &{}-\bigl(e_{2}(k)-e_{2}(k-d_{m}) \bigr)^{T}R_{2}\bigl(e_{2}(k)-e_{2}(k-d_{m}) \bigr), \end{aligned}$$
(15)
$$\begin{aligned} \Delta V_{7}(k) =&h_{M}^{2} \eta_{1}^{T}(k)R_{3}\eta_{1}(k)+d_{M}^{2} \eta_{2}^{T}(k)R_{4}\eta_{2}(k) \\ &{}-h_{M}\sum_{i=k-h_{M}}^{k-1} \eta_{1}^{T}(i)R_{3}\eta_{1}(i) \\ &{}-d_{M}\sum_{i=k-d_{M}}^{k-1} \eta_{2}^{T}(i)R_{4}\eta_{2}(i) \\ \leq &h_{M}^{2}\eta_{1}^{T}(k)R_{3} \eta_{1}(k)+d_{M}^{2}\eta_{2}^{T}(k)R_{4} \eta_{2}(k) \\ &{}-\bigl(e_{1}(k)-e_{1}(k-h_{M}) \bigr)^{T}R_{3}\bigl(e_{1}(k)-e_{1}(k-h_{M}) \bigr) \\ &{}-\bigl(e_{2}(k)-e_{2}(k-d_{M}) \bigr)^{T}R_{4}\bigl(e_{2}(k)-e_{2}(k-d_{M}) \bigr), \\ \Delta V_{8}(k) =&(h_{M}-h_{m})^{2} \eta_{1}^{T}(k)R_{5}\eta _{1}(k)-(h_{M}-h_{m}) \Biggl[\sum_{i=k-h_{M}}^{k-h(k)-1}\eta_{1}^{T}(i)R_{5} \eta _{1}(i) \\ &{}+\sum_{i=k-h(k)}^{k-h_{m}-1}\eta_{1}^{T}(i)R_{5} \eta _{1}(i)\Biggr]+(d_{M}-d_{m})^{2} \eta_{2}^{T}(k)R_{6}\eta_{2}(k) \\ &{}-(d_{M}-d_{m})\Biggl[\sum_{i=k-d_{M}}^{k-d(k)-1} \eta_{2}^{T}(i)R_{6}\eta _{2}(i)+\sum _{i=k-d(k)}^{k-d_{m}-1}\eta_{2}^{T}(i)R_{6} \eta_{2}(i)\Biggr] \\ \leq&(h_{M}-h_{m})^{2}\eta_{1}^{T}(k)R_{5} \eta_{1}(k)-\frac{1}{\frac {h_{M}-h(k)}{h_{M}-h_{m}}}\zeta_{1}^{T}(k)R_{5} \zeta_{1}(k) \\ &{}-\frac{1}{\frac{h(k)-h_{m}}{h_{M}-h_{m}}}\zeta_{2}^{T}(k)R_{5}\zeta _{2}(k)+(d_{M}-h_{m})^{2} \eta_{2}^{T}(k)R_{6}\eta_{2}(k) \\ &{}-\frac{1}{\frac{d_{M}-d(k)}{d_{M}-d_{m}}}\zeta_{3}^{T}(k)R_{6} \zeta_{3}(k)-\frac {1}{\frac{d(k)-d_{m}}{d_{M}-d_{m}}}\zeta_{4}^{T}(k)R_{6} \zeta_{4}(k). \end{aligned}$$
(16)

Using Lemma 2 gives

$$\begin{aligned} \Delta V_{8}(k) \leq&(h_{M}-h_{m})^{2} \eta_{1}^{T}(k)R_{5}\eta_{1}(k)+(d_{M}-d_{m})^{2} \eta _{2}^{T}(k)R_{6}\eta_{2}(k) \\ &{}- \left .\begin{bmatrix} \zeta_{1}(k)\\ \zeta_{2}(k) \end{bmatrix} \right .^{T} \begin{bmatrix} R_{5}&S_{1}\\ \star&R_{5} \end{bmatrix} \begin{bmatrix} \zeta_{1}(k)\\ \zeta_{2}(k) \end{bmatrix} \\ &{}- \left .\begin{bmatrix} \zeta_{3}(k)\\ \zeta_{4}(k) \end{bmatrix} \right .^{T} \begin{bmatrix} R_{6}&S_{2}\\ \star&R_{6} \end{bmatrix} \begin{bmatrix} \zeta_{3}(k)\\ \zeta_{4}(k) \end{bmatrix}, \end{aligned}$$
(17)

where \(\zeta_{1}(k)=e_{1}(k-h(k))-e_{1}(k-h_{M})\), \(\zeta_{2}(k)=e_{1}(k-h_{m})-e_{1}(k-h(k))\), \(\zeta_{3}(k)=e_{2}(k-d(k))-e_{2}(k-d_{M})\), \(\zeta_{4}(k)=e_{2}(k-d_{m})-e_{2}(k-d(k))\).

Obviously, \(\zeta_{1}(k)=0\), or \(\zeta_{2}(k)=0\), if \(h(k)=h_{M}\) or \(h(k)=h_{m}\). Similarly, \(\zeta_{3}(k)=0\), or \(\zeta_{4}(k)=0\), if \(d(k)=d_{M}\) or \(d(k)=d_{m}\).

Hence, for any matrices \(L_{1}\) and \(L_{2}\) with appropriate dimensions, we get

$$ \begin{aligned} &2e_{1}^{T}(k+1)L_{1} \bigl[e_{1}(k+1)-(A-K_{1}M_{1})e_{1}(k)-C \xi_{1}(k) -E\xi _{1}\bigl(k-d(k)\bigr)\bigr]=0, \\ &2e_{2}^{T}(k+1)L_{2}\bigl[e_{2}(k+1)-(B-K_{2}M_{2})e_{2}(k)-D \xi_{2}(k) -W\xi_{2}\bigl(k-h(k)\bigr)\bigr]=0. \end{aligned} $$
(18)

Moreover, it follows from Assumption 1 that

$$\begin{aligned} \bigl[\xi_{1i}(k)-F_{i}^{-}e_{2i}(k)\bigr] \bigl[ \xi_{1i}(k)-F_{i}^{+}e_{2i}(k)\bigr]\leq0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \left .\begin{bmatrix} e_{2}(k)\\ \xi_{1}(k) \end{bmatrix} \right .^{T} \begin{bmatrix} F_{i}^{-}F_{i}^{+}e_{i}e_{i}^{T}&-\frac{F_{i}^{-}+F_{i}^{+}}{2}e_{i}e_{i}^{T}\\ \star&e_{i}e_{i}^{T} \end{bmatrix} \begin{bmatrix} e_{2}(k)\\ \xi_{1}(k) \end{bmatrix} \leq0, \end{aligned}$$

where \(e_{i}\) denotes the unit column vector having an element on its ith row and zeros elsewhere. For positive diagonal matrices \(U_{k}=\operatorname{diag}(u_{k1},u_{k2},\ldots,u_{kn})\), \(k=1,2,3,4\):

$$\begin{aligned} \sum_{i=1}^{n}u_{1i} \left .\begin{bmatrix} e_{2}(k)\\ \xi_{1}(k) \end{bmatrix} \right .^{T} \begin{bmatrix} F_{i}^{-}F_{i}^{+}e_{i}e_{i}^{T}& -\frac{F_{i}^{-}+F_{i}^{+}}{2}e_{i}e_{i}^{T}\\ \star&e_{i}e_{i}^{T} \end{bmatrix} \begin{bmatrix} e_{2}(k)\\ \xi_{1}(k) \end{bmatrix}\leq0, \end{aligned}$$

that is,

$$ \left .\begin{bmatrix} e_{2}(k)\\ \xi_{1}(k) \end{bmatrix} \right .^{T} \begin{bmatrix} F_{1}U_{1}&-F_{2}U_{1}\\ \star&U_{1} \end{bmatrix} \begin{bmatrix} e_{2}(k)\\ \xi_{1}(k) \end{bmatrix}\leq0. $$
(19)

Similarly, for any positive diagonal matrices \(U_{2}\), \(U_{3}\), \(U_{4}\), we obtain

$$\begin{aligned}& \left .\begin{bmatrix} e_{2}(k-d(k))\\ \xi_{1}(k-d(k)) \end{bmatrix} \right .^{T} \begin{bmatrix} F_{1}U_{2}&-F_{2}U_{2}\\ \star&U_{2} \end{bmatrix} \begin{bmatrix} e_{2}(k-d(k))\\ \xi_{1}(k-d(k)) \end{bmatrix}\leq0, \end{aligned}$$
(20)
$$\begin{aligned}& \left .\begin{bmatrix} e_{1}(k)\\ \xi_{2}(k) \end{bmatrix} \right .^{T} \begin{bmatrix} G_{1}U_{3}&-G_{2}U_{3}\\ \star&U_{3} \end{bmatrix} \begin{bmatrix} e_{1}(k)\\ \xi_{2}(k) \end{bmatrix}\leq0, \end{aligned}$$
(21)
$$\begin{aligned}& \left .\begin{bmatrix} e_{1}(k-h(k))\\ \xi_{2}(k-h(k)) \end{bmatrix} \right .^{T} \begin{bmatrix} G_{1}U_{4}&-G_{2}U_{4}\\ \star&U_{4} \end{bmatrix} \begin{bmatrix} e_{1}(k-h(k))\\ \xi_{2}(k-h(k)) \end{bmatrix}\leq0. \end{aligned}$$
(22)

Combining all the above inequalities, we deduce

$$ \Delta V(k)\leq u^{T}(k)\Phi u(k), $$
(23)

where \(u(k)\)=\([e_{1}^{T}(k+1)\),\(e_{1}^{T}(k)\),\(e_{1}^{T}(k-h(k))\),\(e_{1}^{T}(k-h_{m})\),\(e_{1}^{T}(k-h_{M})\),\(\xi _{1}^{T}(k)\),\(\xi_{1}^{T}(k-d(k))\), \(e_{2}^{T}(k+1)\),\(e_{2}^{T}(k)\),\(e_{2}^{T}(k-d(k))\),\(e_{2}^{T}(k-d_{m})\),\(e_{2}^{T}(k-d_{M})\),\(\xi _{2}^{T}(k)\),\(\xi_{2}^{T}(k-h(k))]^{T}\) and Φ is defined as in (8).

Combined (23) with (7) and (8), it can be deduced that there exists a scalar \(\sigma< 0\) and \(|\sigma| <\lambda _{\max}(P_{1})+\lambda_{\max}(P_{2})\) such that

$$ \Delta V(k)\leq\sigma\bigl(\bigl\| e_{1}(k)\bigr\| ^{2}+ \bigl\| e_{2}(k)\bigr\| ^{2}\bigr). $$
(24)

Now we are in a position to prove the global exponential stability of the error system (5). Firstly, from the definition of \(V(k)\), it can be verified that

$$\begin{aligned} V(k) \leq&\lambda_{\max}(P_{1}) \bigl\| e_{1}(k)\bigr\| ^{2}+\lambda _{\max}(P_{2}) \bigl\| e_{2}(k)\bigr\| ^{2} \\ &{}+\sigma_{1}\sum_{i=k-h_{M}}^{k-1} \bigl\| e_{1}(i)\bigr\| ^{2}+\sigma_{2}\sum _{i=k-d_{M}}^{k-1}\bigl\| e_{2}(i)\bigr\| ^{2}, \end{aligned}$$
(25)

where \(\sigma_{1}=(h_{M}-h_{m}+1)\lambda_{\max}(Q_{1})+\lambda_{\max}(Q_{3})+\lambda _{\max}(Q_{5})+4h_{m}^{2}\lambda_{\max}(R_{1})+4h_{M}^{2}\lambda_{\max}(R_{3}) +4(h_{M}-h_{m})^{2}\lambda_{\max}(R_{5})\), \(\sigma_{2}=(d_{M}-d_{m}+1)\lambda_{\max}(Q_{2})+\lambda_{\max}(Q_{4})+\lambda _{\max}(Q_{6})+4d_{m}^{2}\lambda_{\max}(R_{2})+4d_{M}^{2}\lambda_{\max}(R_{4}) +4(d_{M}-d_{m})^{2}\lambda_{\max}(R_{6})\).

Consider the following equation:

$$ \sigma r+(r-1) \bigl(\lambda_{\max}(P_{1})+ \lambda_{\max}(P_{2})\bigr)+(r-1) (\sigma _{1}+ \sigma_{2}) \bigl(h_{M}r^{h_{M}}+d_{M}r^{d_{M}} \bigr)=0. $$
(26)

The solution of equation (26)

$$r=\frac{\lambda_{\max}(P_{1})+\lambda_{\max}(P_{2})+(\sigma_{1}+\sigma _{2})(h_{M}r^{h_{M}}+d_{M}r^{d_{M}})}{\lambda_{\max}(P_{1}) +\lambda_{\max}(P_{2})+(\sigma_{1}+\sigma_{2})(h_{M}r^{h_{M}}+d_{M}r^{d_{M}})+\sigma}. $$

Obviously \(r>1\).

It follows from (24) and (25) that

$$\begin{aligned} r^{k+1}V(k+1)-r^{k}V(k) =&r^{k+1} \Delta V(k)+r^{k}(r-1)V(k) \\ \leq&\sigma_{3}r^{k}\bigl(\bigl\| e_{1}(k) \bigr\| ^{2}+\bigl\| e_{2}(k)\bigr\| ^{2}\bigr) \\ &{}+\sigma_{4}r^{k}\Biggl(\sum _{i=k-h_{M}}^{k-1}\bigl\| e_{1}(i)\bigr\| ^{2}+\sum _{i=k-d_{M}}^{k-1}\bigl\| e_{2}(i) \bigr\| ^{2}\Biggr), \end{aligned}$$
(27)

where \(\sigma_{3}=\sigma r+(r-1)(\lambda_{\max}(P_{1})+\lambda_{\max}(P_{2}))\), \(\sigma_{4}=(r-1)(\sigma _{1}+\sigma_{2})\).

Moreover, for any positive integer \(n\geq \max\{h_{M}+1,d_{M}+1\}\), by summing up both sides of (27) from 0 to \(n-1\) with respect to k, we get the following inequality:

$$\begin{aligned} r^{n}V(n)-V(0) \leq&\sigma_{3}\sum _{k=0}^{n-1}r^{k}\bigl(\bigl\| e_{1}(k) \bigr\| ^{2}+\bigl\| e_{2}(k)\bigr\| ^{2}\bigr) \\ &{}+\sigma_{4}\sum_{k=0}^{n-1}r^{k} \Biggl(\sum_{i=k-h_{M}}^{k-1}\bigl\| e_{1}(i) \bigr\| ^{2}+\sum_{i=k-d_{M}}^{k-1} \bigl\| e_{2}(i)\bigr\| ^{2}\Biggr). \end{aligned}$$
(28)

Noting that the time-varying delays \(h_{M}\geq1\) and \(d_{M}\geq1\), we have

$$\begin{aligned} \sum_{k=0}^{n-1}\sum _{i=k-h_{M}}^{k-1}r^{k}\bigl\| e_{1}(i) \bigr\| ^{2} \leq&\Biggl(\sum_{i=-h_{M}}^{-1}\sum _{k=0}^{i+h_{M}} +\sum_{i=0}^{n-1-h_{M}} \sum_{k=i+1}^{i+h_{M}} +\sum_{i=n-h_{M}}^{n-1}\sum _{k=i+1}^{i+h_{M}}\Biggr)r^{k} \bigl\| e_{1}(i)\bigr\| ^{2} \\ \leq& h_{M}\sum_{i=-h_{M}}^{-1}r^{i+h_{M}} \bigl\| e_{1}(i)\bigr\| ^{2} +h_{M}\sum_{i=0}^{n-1-h_{M}}r^{i+h_{M}} \bigl\| e_{1}(i)\bigr\| ^{2} \\ &{}+h_{M}\sum_{i=n-1-h_{M}}^{n-1}r^{i+h_{M}} \bigl\| e_{1}(i)\bigr\| ^{2} \\ \leq& h_{M}(h_{M}+1)r^{h_{M}}\sup _{-h_{M}\leq i\leq0}\bigl\| e_{1}(i)\bigr\| ^{2} +h_{M}r^{h_{M}}\sum_{i=0}^{n-1}r^{i} \bigl\| e_{1}(i)\bigr\| ^{2}. \end{aligned}$$
(29)

Similarly, we can get

$$\begin{aligned} \sum_{k=0}^{n-1}\sum _{i=k-d_{M}}^{k-1}r^{k}\bigl\| e_{2}(i) \bigr\| ^{2} \leq&d_{M}(d_{M}+1)r^{d_{M}}\sup _{-d_{M}\leq i\leq0}\bigl\| e_{2}(i)\bigr\| ^{2} +d_{M}r^{d_{M}}\sum_{i=0}^{n-1}r^{i} \bigl\| e_{2}(i)\bigr\| ^{2}. \end{aligned}$$
(30)

Combining (28) with (29) and (30) yields

$$\begin{aligned} r^{n}V(n) \leq&\bigl[\sigma_{3}+ \sigma_{4}\bigl(h_{M}r^{h_{M}}+d_{M}r^{d_{M}} \bigr)\bigr]\sum_{k=0}^{n-1}r^{k} \bigl(\bigl\| e_{1}(k)\bigr\| ^{2}+\bigl\| e_{2}(k)\bigr\| ^{2} \bigr) \\ &{}+\sigma_{4}\bigl[h_{M}(h_{M}+1)r^{h_{M}}+d_{M}(d_{M}+1)r^{d_{M}} \bigr] \\ &{}\times\Bigl(\sup_{-h_{M}\leq i\leq0}\bigl\| e_{1}(i) \bigr\| ^{2}+\sup_{-d_{M}\leq i\leq0}\bigl\| e_{2}(i)\bigr\| ^{2}\Bigr)+V(0). \end{aligned}$$
(31)

It follows from (25) that

$$\begin{aligned} V(0) \leq&\bigl[\lambda_{\max}(P_{1})+ \sigma_{1}h_{M}\bigr]\sup_{-h_{M}\leq i\leq0}\bigl\| e_{1}(i)\bigr\| ^{2} \\ &{}+\bigl[\lambda_{\max}(P_{2})+\sigma_{2}d_{M} \bigr]\sup_{-d_{M}\leq i\leq 0}\bigl\| e_{2}(i)\bigr\| ^{2} \\ \leq&d\Bigl[\sup_{-h_{M}\leq i\leq 0}\bigl\| e_{1}(i) \bigr\| ^{2}+\sup_{-d_{M}\leq i\leq0}\bigl\| e_{2}(i)\bigr\| ^{2}\Bigr], \end{aligned}$$
(32)

where \(d=\max\{\lambda_{\max}(P_{1})+\sigma_{1}h_{M},\lambda_{\max}(P_{2})+\sigma_{2}d_{M}\} \). Again, from (9) we can observe that

$$\begin{aligned} V(n) \geq&V_{1}(n) \\ \geq& \min\bigl\{ \lambda _{\min}(P_{1}), \lambda_{\min}(P_{2})\bigr\} \bigl[\bigl\| e_{1}(n) \bigr\| ^{2}+\bigl\| e_{2}(n)\bigr\| ^{2}\bigr]. \end{aligned}$$
(33)

Substituting (26), (32) and (33) into (31), we get

$$ \bigl\| e_{1}(n)\bigr\| ^{2}+\bigl\| e_{2}(n) \bigr\| ^{2}\leq\lambda r^{-n}\Bigl(\sup_{-h_{M}\leq i\leq 0}\bigl\| e_{1}(i)\bigr\| ^{2}+\sup_{-d_{M}\leq i\leq0}\bigl\| e_{2}(i)\bigr\| ^{2}\Bigr), $$
(34)

where \(\lambda=\frac{d+\sigma _{4}[h_{M}(h_{M}+1)r^{h_{M}}+d_{M}(d_{M}+1)r^{d_{M}}]}{\min\{\lambda_{\min}(P_{1}),\lambda _{\min}(P_{2})\}}\). Therefore, the error system (5) is globally exponentially stable. This completes the proof. □

Remark 2

A state estimator to the neuron states is designed through available output measurements in our paper. A new sufficient condition is established to ensure the global exponential stability of the error system (5) in this paper. The numerical complexity of Theorem 1 in this paper is proportional to \(13n^{2}+11n\). However, only the sufficient condition is established to ensure the global asymptotical stability of the error system in [27]. The numerical complexity of Theorem 3.1 in [27] is proportional to \(29n^{2}+25n\). It is obvious that Theorem 1 in this paper has lower computational complexity.

Corollary 1

Suppose that \(h(k)=h\), and \(d(k)=d\) are constant scalars. Then, under Assumption  1, the error system (5) is globally exponentially stable if there exist positive matrices \(P_{i}\), \(Q_{i}\), \(R_{i}\), \(i=1,2\), positive diagonal matrices \(U_{j}>0\) (\(j=1,2,3,4\)), and matrices \(L_{1}\), \(L_{2}\), X, Y of appropriate dimensions such that the following LMIs hold:

$$ \Phi=[\Phi_{ij}]_{10\times10} < 0, $$
(35)

where \(\Phi _{1,1}=P_{1}+h^{2}R_{1}+L_{1}+L_{1}^{T}\), \(\Phi_{1,2}=-h^{2}R_{1}-L_{1}A+XM_{1}\), \(\Phi _{1,4}=-L_{1}C\), \(\Phi_{1,5}=-L_{1}E\), \(\Phi_{2,2}=P_{1}+Q_{1}+(h^{2}-1)R_{1}-G_{1}U_{3}\), \(\Phi_{2,3}=R_{1}\), \(\Phi_{2,9}=G_{2}U_{3}\), \(\Phi_{3,3}=-Q_{1}-R_{1}-G_{1}U_{4}\), \(\Phi_{3,10}=G_{2}U_{4}\), \(\Phi_{4,4}=-U_{1}\), \(\Phi_{4,7}=F_{2}U_{1}\), \(\Phi_{5,5}=-U_{2}\), \(\Phi_{5,8}=F_{2}U_{2}\), \(\Phi_{6,6}=P_{2}+d^{2}R_{2}+L_{2}+L_{2}^{T}\), \(\Phi _{6,7}=-d^{2}R_{2}-L_{2}A+YM_{2}\), \(\Phi_{6,9}=-L_{2}D\), \(\Phi_{6,10}=-L_{2}W\), \(\Phi _{7,7}=P_{2}+Q_{2}+(d^{2}-1)R_{2}-F_{1}U_{1}\), \(\Phi_{7,8}=R_{1}\), \(\Phi _{8,8}=-Q_{2}-R_{2}-F_{1}U_{2}\), \(\Phi_{9,9}=-U_{3}\), \(\Phi_{10,10}=-U_{4}\), and other terms are zeros.

4 Illustrative example

In this section, we provide a numerical example to illustrate the effectiveness of our result.

Consider system (1) and the measurement outputs (2) with the following parameters:

$$\begin{aligned}& A= \begin{bmatrix} 0.05&0\\ 0&0.04 \end{bmatrix},\qquad C= \begin{bmatrix} -0.03&-0.01\\ 0.01&0.03 \end{bmatrix},\qquad E= \begin{bmatrix} 0.04&-0.04\\ 0.20&0.02 \end{bmatrix}, \\& M_{1}= \begin{bmatrix} 0.40&0\\ 0.10&-0.10 \end{bmatrix},\qquad B= \begin{bmatrix} 0.01&0\\ 0&0.03 \end{bmatrix}, \qquad D= \begin{bmatrix} -0.02&-0.01\\ 0.01&-0.02 \end{bmatrix}, \\& W= \begin{bmatrix} 0.01&-0.04\\ -0.20&0.03 \end{bmatrix},\qquad M_{2}= \begin{bmatrix} 0.24&0\\ 0&0.61 \end{bmatrix}. \end{aligned}$$

The activation functions are described by \(f_{1}(y(k))=0.8\tanh(y(k))\), \(f_{2}(y(k))=-0.4\tanh(y(k))\), \(g_{1}(x(k))=0.8\tanh(x(k))\), \(g_{2}(x(k))=-0.4\tanh(x(k))\). Further, it follows from Assumption 1 that \(F_{1}=G_{1}=\operatorname{diag}\{0,0\}\), \(F_{2}=G_{2}=\operatorname{diag}\{0.8,-0.4\}\).

By using the MATLAB LMI toolbox, we can obtain the feasible solution which is not given here due to the page constraint. If we choose the lower delay bound as \(h_{m}=d_{m}=7.0\), the upper delay bounds are \(h_{M}=d_{M}=90\), then the corresponding state estimation gain matrices \(K_{1}\) and \(K_{2}\) can be obtained as follows:

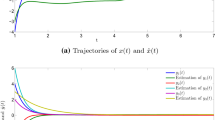
$$K_{1}=L_{1}^{-1}X= \begin{bmatrix} 0.1189&-0.0036\\ 0.1508&-0.5897 \end{bmatrix}, \qquad K_{2}=L_{2}^{-1}Y= \begin{bmatrix} 0.2044&-0.0002\\ -0.0390&0.0580 \end{bmatrix}. $$

We choose the initial values \(x(0)=[0.5 ,0.9]^{T}\), \(\widehat {x}(0)=[-0.9 ,-0.4]^{T}\), \(y(0)=[0.7 ,0.9]^{T}\) and \(\widehat{y}(0)=[-0.2 ,-0.5]^{T}\). The simulation results for state response and estimation error are shown in Figures 1-6. Figures 1-4 show the response of the state dynamics of \((x(k),\widehat{x}(k))\) and \((y(k),\widehat{y}(k))\). The estimation errors \(e_{1}(k)\) and \(e_{2}(k)\) are shown in Figures 5 and 6. The result reveals that the error state goes to zero after a short period time. We conclude that system (3) is a proper estimator of the BAM neural networks (1), which also demonstrates the effectiveness of our design approach.

Figure 1
figure 1

State trajectories of \(\pmb{x_{1}(k)}\) and its estimations.

Full size image
Figure 2
figure 2

State trajectories of \(\pmb{x_{2}(k)}\) and its estimations.

Full size image
Figure 3
figure 3

State trajectories of \(\pmb{y_{1}(k)}\) and its estimations.

Full size image
Figure 4
figure 4

State trajectories of \(\pmb{y_{2}(k)}\) and its estimations.

Full size image
Figure 5
figure 5

State trajectories of errors \(\pmb{e_{1}(k)}\) .

Full size image
Figure 6
figure 6

State trajectories of errors \(\pmb{e_{2}(k)}\) .

Full size image

5 Conclusions

In this paper, the problem of state estimation for BAM discrete-time neural network with time-varying delays has been studied. Based on the delay partitioning method, the reciprocally convex approach and a new Lyapunov-Krasovskii functional, a new set of sufficient conditions which guarantee the global exponential stability of the error system is derived. A numerical example is presented to demonstrate that the new criterion has lower computational complexity than previously reported criteria.