Abstract
The future sixth generation (6G) is going to face the significant challenges of massive connections and green communication. Recently, reconfigurable intelligent surfaces (RIS) and non-orthogonal multiple access (NOMA) have been proposed as two key technologies to solve the above problems. Motivated by this fact, we consider a downlink RIS-aided NOMA system, where the source aims to communicate with the two NOMA users via RIS. Considering future network supporting real-time service, we investigate the system performance with the view of effective capacity (EC), which is an important evaluation metric of delay sensitive systems. Specifically, we derive the analytical expressions of the EC of the near and far users. To obtain more useful insights, we deduce the analytical approximation expressions of the EC in the low signal-to-noise-ratio approximation by utilizing Taylor expansion. Moreover, we provide the results of orthogonal multiple access (OMA) for the purpose of comparison. It is found that (1) The number of RIS components and the transmission power of the source have important effects on the performance of the considered system; (2) Compared with OMA, NOMA system has higher EC due to the short transmission time.
Similar content being viewed by others
1 Introduction
For the past few years, the sixth generation (6G) mobile communication technology has attracted a lot of attentions because of its high transmission rate, high reliability and high capacity. Thus, it has great practical and economic values for the industry and Internet of Things (IoT) [1,2,3,4]. The application scenario of the IoT is an integration of a variety of emerging technologies, which has become the most popular research at present. The rise of the IoT has put forward higher requirements for communication technology. On the other hand, the main challenges of future wireless networks are large-scale access, high energy consumption and hardware costs. Therefore, it is imperative to find solutions with low power consumption and high economic benefits for future wireless networks to meet users’ high requirements for quality of service (QoS) and data rate [5, 6]. Fortunately, the concepts of ambient backscatter and reconfigurable intelligent surface (RIS), which are passive devices, have been introduced into wireless communication research [7,8,9]. And instead of using active transmitters, they utilize the surrounding radio frequency (RF) signals as a passive source, thus not resulting in extra power consumption and no need for specialized energy supply [10]. The difference between backscatter and RIS is that the orientations of reflected signals using RIS are controlled by phase angles. Therefore, RIS performs better in solving the problem of energy consumption and hardware cost reduction in wireless communication systems.
As a new paradigm, RIS is equipped with multiple reflective elements composed of two-dimensional artificial electromagnetic materials. Each reflective element is controlled by the software, then the reflected phase and angle of the incident RF signal can be flexibly adjusted. By adjusting the phase angle of RIS, the ideal effect is obtained and the performance of wireless communication system is improved [11]. RIS can be flexibly configured on walls, ceilings, and outer surfaces of buildings, and the channel capacity can be effectively increased with the participation of RIS. It has extremely low power consumption and is friendly to the environment, which can availably improve the energy efficiency of the communication systems [12]. Compared with the existing technologies, RIS can achieve deterministic and programmable control of wireless environment behavior. Based on these advantages, a great deal of research works have focused on these aspects of RIS. In [13], the authors developed an optimization of joint the transmit power allocation and the phases shifts of the surface reflecting elements of each link to maximize energy efficient of downlink RIS-assisted multi-user communication systems. To maximize the energy efficiency for all users, the authors in [14] put forward a joint radio resource and passive beamforming optimization scheme, which adopted the Lagrange dual theory and a semidefinite programming method for the downlink RIS-assisted wireless-powered communication network. An outage-constrained beamforming algorithm for RIS-assisted wireless-powered communication networks was proposed in [15]. The author solved the issue of minimizing the total transmission power of the RIS wireless system in [16]. For the performance analysis aspects, Jung et al. analyzed the reliability of the RIS systems and derived the expressions for the sum rate of the uplink RIS systems as well as outage probability [17]. The authors of [18] analyzed the capacity degradation problem of RIS network with hardware impairments. In addition, some researchers also studied RIS in combination with other promising technologies, such as millimeter wave (mmWave) multiple-input multiple-output (MIMO), simultaneous wireless information and power transfer (SWIPT) and non-orthogonal multiple access (NOMA). In [19], the channel estimation scheme of RIS-aided mmWave MIMO system was designed through adopting a two-stage iterative reweighted method to obtained the perfect channel state information. In [20], the authors proposed an adaptive phase shifter design of RIS-aided mmWave MIMO system based on the hierarchical codebooks and mobile station feedback. Ding et al. [21] proposed a simple design of RIS-assisted NOMA downlink transmission, which can improve the spectral efficiency and connectivity. Further, the authors maximized the sum rate of all users by using semidefinite relaxation method in [22]. All these above studies show a bright future for RIS in combination with other technologies.
NOMA is another promising technology for the beyond fifth generation (B5G) which has attracted wide attention in academia and industry [23,24,25,26]. NOMA is considered to have obvious advantages in solving problems of spectrum scarce and devices access, and is an effective method to solve large-scale access and QoS [27, 28]. The pivotal idea of NOMA is that multiple users at the transmitter and receiver share the same time/frequency domain resources, and the transmitter directly sends the superposition codes of multiple users. In order to ensure fairness, the allocation power to users is inversely proportional with channel gain. That is, users with large channel gain allocate less power, vice versa. At the receivers, the interference information can be recovered by using successive interference cancellation (SIC) [29]. To this end, NOMA technology has been widely recognized as an effective solution to improve the quality of mobile network access, and has been identified as a promising prospect [30]. However, the NOMA technology is not without its drawbacks. The realization of NOMA technology requires high-complexity and/or multiple equipments. It is difficult to achieve good performance with NOMA alone when the wireless system has numerous users. Fortunately, RIS provides a new idea for this situation. Many studies have also shown that RIS can effectively improve the NOMA system’s performance. In [31], the performances of NOMA and orthogonal multiple access (OMA) of the RIS-assisted downlink communication network were compared, and a low-complexity algorithm with close to optimal performance was proposed. Reference [32] studied coherent phase shifting and random discrete phase shifting on the impact of the RIS-aided NOMA system. The performance of physical layer security was studied in [33]. The outage probability of the RIS-aided NOMA system with hardware impairments was derived in [34]. Further, authors in [35] investigated the physical layer security of the RIS-aided NOMA system in the presence of an eavesdropper with residual hardware impairments, where the expression for the secrecy outage probability of the considered systems was obtained.
It is noted that the current researches on the RIS-aided NOMA communication system mainly focus on the analysis of channel capacity and outage probability, etc., and have not considered the influence of delay on system performance. Thus, it is impossible to make an accurate analysis of the communication real-time business requirements. For purpose of analyzing the influence of delay on the communication system, Wu et al. put forward the concept of effective capacity (EC) in [36], which is used to quantify the accessibility of various wireless systems under the limit of the delay QoS. EC can provide a key point to characterize the impact of statistical delay QoS on system performance. In addtion, in [37], a unified pattern for analyzing effective rate in wireless communication system based on multi-input single-output (MISO) with arbitrary correlated generalized K fading channels and hyper Fox’s H fading channels was proposed. To reduce complexity and energy consumption, a transmit antenna selection (TAS) scheme was designed, and the closed form expression of MISO TAS systems was derived in [38]. The work of [38] was further extended into generalized fading channels in [39], where the approximate EC of MISO systems with \(\kappa - \mu\) shadowing fading channels was investigated by using moment matching method. Moreover, the EC of Rician fading channels of MISO systems was derived in [40], and the EC of Weibull fading channels of MISO systems was derived in [41]. To get the impact of system parameters and make a further study, they all derived the tractable expressions of EC in both high and low signal-to-noise-ratio (SNR) regions.
To the best of the authors knowledge, the effects of delay and QoS on the performance of RIS-assisted NOMA systems have not been studied in the open literature. The very few works have been published in [34]–[41]. The authors of [34] studied the outage probability of the RIS-aided NOMA system with hardware impairments, yet, the effect of delay on the RIS-aided NOMA system was not involved. The authors of [42] considered NOMA with delay QoS constraints and EC with power control. On the similar grounds, the promising RIS technology is not taken into account. The approximated effective rate of RIS-assisted communications was analyzed by deriving closed-form expressions in [43]. However it considers the traditional OMA scenario. Compared with the above works, the main contribution of this paper is to study the effect of delay on the RIS-assisted NOMA system performance and accommodate delay QoS constraints so that NOMA can be employed for delay-sensitive transmissions. The details of this paper’s contributions are summarized as follows:
-
We consider a downlink RIS-aided NOMA system, where the source (S) sends information to two users by using NOMA protocol with the aid of RIS with N reflection elements. Considering delay-sensitive requirements, we introduce a key performance evaluation metric of EC into the considered system.
-
We first derive the approximate expressions for the EC of the near and far users. The EC of RIS-aided NOMA system for the near user (NU) relies on transmission power, power allocation coefficients (\({{\xi _n}}\), \({{\xi _f}}\)), number of RIS N, QoS exponent \(\alpha\), bandwith B, while the EC for the far user (FU) only determined by bandwith B and power allocation factors (\({{\xi _n}}\), \({{\xi _f}}\)).
-
We deduce the asymptotic behavior of EC in the low SNR approximation by invoking Taylor expansion. Moreover, in order to compare, we provide the results of OMA.
The rest of this paper’s structure is as follows. The system model of this paper and the concept of the EC are introduced in Sect. 2. In Sect. 3, we derive the analytical expression for the EC of RIS-aided NOMA system as well as the asymptotic analysis in the low SNR area. The simulation results and the conclusion of this paper are given in Sects. 3.2 and 4, respectively.
The main notations used in this paper are as follows. In this paper, we use capital boldface to indicate a matrix and lowercase boldface to indicate a vector. We use \({\hbox {E}}\left\{ {{\cdot }} \right\}\) for the expectation operation. Bessel functions of the second kind are denoted by \({K_v}\left( {{\cdot }} \right)\). The conjugate transpose of a matrix or vector is denoted by the notations \({\left( {{\cdot }} \right) ^H}\). \({{\mathcal {C}}}{{\mathcal {N}}} \sim \left( {\mu ,{\sigma ^2}} \right)\) denotes Gaussian which has the mean of \(\mu\) and the variance of \({{\sigma ^2}}\). The probability density function (PDF) of a random variable X is expressed by \({f_X}( \cdot )\).
2 Methods
2.1 System model
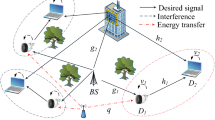
We consider a RIS-aided NOMA network as illustrated in Fig. 1, which includes a S, a RIS consists with N reflection elements, a FU and a NU. There is no direct connection between the S and the users due to the heavy shadowing and/or obstacle. We assume that: (1) All nodes are single antenna; (2) All channels obey independent Rayleigh fading. It is noted that although the Rayleigh channel is not fully applicable in the physical model of RIS, for the sake of simple analysis, the Rayleigh channel is adopted in this paper, and other fading channels will be studied in our future research. We denote \({{\mathbf {h}}_{\mathrm{sr}}} = \left[ {h_{\mathrm{sr}}^1...h_{\mathrm{sr}}^n...h_{\mathrm{sr}}^N} \right]\), where \({{\mathbf {h}}_{\mathrm{sr}}} \sim \left( {0,{\Omega _{\mathrm{sr}}}} \right)\) as the baseband equivalent fading channels between S and RIS. \({{\mathbf {h}}}_{\mathrm{rn}} = \left[ {h_{\mathrm{rn}}^1...h_{\mathrm{rn}}^n...h_{\mathrm{rn}}^N} \right]\) and \({{\mathbf {h}}}_{\mathrm{rf}} = \left[ {h_{\mathrm{rf}}^1...h_{\mathrm{rf}}^n...h_{\mathrm{rf}}^N} \right]\), respectively, denote channels from the RIS to NU and FU, where \({{\mathbf {h}}}_{\mathrm{rn}} \sim \left( {0,{\Omega _{\mathrm{rn}}}} \right)\) and \({{\mathbf {h}}}_{\mathrm{rf}} \sim \left( {0,{\Omega _{\mathrm{rf}}}} \right)\).
According to the NOMA principle, the S first sends superposed signals to NU and FU. The total transmit power of the S is denoted by \({{P_s}}\). The power allocation coefficients of NU and FU are \({{\xi _n}}\) and \({{\xi _f}}\) with \({\xi _n} < {\xi _f}\), \({\xi _n} + {\xi _f} = 1\), respectively. Following principle of NOMA, the received signals at users are given as
where \({\varvec{\Theta }} = {\text {diag}}\left( {\beta {e^{j{\theta _1}}},...,\beta {e^{j{\theta _n}}},...,\beta {e^{j{\theta _N}}}} \right)\) is a diagonal matrix, \(\beta \in \left[ {0,1} \right]\) denotes the fixed reflection amplitude coefficient and \({\theta _n} \in \left[ {0,2\pi } \right)\) denotes the phase shift of the n-th reflecting element of the RIS. \({n_n}\) and \({n_f}\) are the additive white Gaussian noise (AWGN) at NU and FU with satisfying \({n_n} \sim {{\mathcal {N}}}\left( {0,\sigma _n^2} \right)\) and \({n_f} \sim {{\mathcal {N}}}\left( {0,\sigma _f^2} \right)\).
For NU, by using the NOMA protocol, interference from FU is eliminated due to the existence of SIC, then the signal-to-interference-plus-noise-ratio (SINR) of NU can be given as
For FU, different from NU, the interference from NU cannot be cancelled. Thus, we obtain SINR at FU as
2.2 Effective capacity
Effective capacity is the maximum constant arrival rate at the queue of the transmitter under the condition of satisfying statistical QoS constraints [36]. The mathematical expression is given by
where t is the block-length; \({s\left( t \right) }\) is the cumulative service process; \(\alpha\) is QoS exponent, which is related with both delay violation probability and length of a queue. When \(\alpha\) approaches zero, it corresponds to delay tolerance communication, while when \(\alpha\) approaches infinity, it turns to delay limited communication. It is given by
where L is the equilibrium queue-length of the buffer at the transmitter.
In this study, it is assumed that the S has perfect channel state information (CSI), so cumulative service process \(s\left( t \right)\) at time slot t can be represented by Shannon capacity \(c\left( t \right)\). The mathematical expression of \(c\left( t \right)\) can be given by
where B is bandwidth.
We assume that independent and identical block fading channels, so Eq. (5) can be rewritten as
3 Performance analysis
In this section, we derive the approximate analytical closed-form expressions for the EC of NU and FU in the high and low SNRs. In high SNR regions, we use the dominant term to approximate SINR, and carry out the approximate analysis. While in the low SNR analysis, we deduce the asymptotic analysis by invoking the Taylor series.
3.1 Approximate analysis
In this section, we derive the closed-form expressions of EC of NU and FU, which are obtained by taking SNR large.
Theorem 1
The closed-form expression at NU is given by
where \(\Gamma \left( {{\cdot }} \right)\) is the gamma function.
Proof
See the “Appendix 1”. \(\square\)
Theorem 2
The closed-form expression at FU is given by
Proof
See the “Appendix 2”. \(\square\)
Remark 1
Because the high SNR approximation is used in the calculation, from Theorems 1 and 2, we can see that: (1) For NU, the EC is logarithmic to the transmit power \({{P_s}}\) and channel parameters \({{\sigma _a}, {\sigma _b}}\); (2) The EC value of FU is a constant in the high SNR.
3.2 Low-SNR approximate analysis
For the case of low SNR, a similar methodology to that in [39] is adopted. At NU and FU, \(\gamma \rightarrow {{{0}}^{{ + }}}\), the second-order Taylor expansion of SNR is used. The expression of EC is given by
where \(\mathop {{\text {EC}}}\limits ^ \cdot \left( \alpha \right)\) and \(\mathop {{\text {EC}}}\limits ^{ \cdot \cdot } \left( \alpha \right)\) denote the first- and second-order derivatives of the approximate EC with regard to the SNR \(\gamma \rightarrow {{{0}}^{{ + }}}\), respectively.
For NU, they can be shown that
where \(Q={\xi _n}{\beta ^2}{\left( {{{\mathbf {a}}^T}{\mathbf {b}}} \right) ^2}\), using Eq. (24) of “Appendix 1”, the mean values of Q and \({{Q^2}}\) can be, respectively, given by
Substitute Eqs. (12)–(15) into Eq. (11), we obtain the EC expression of NU with low SNR approximation.
Similarly, we can obtain FU by using the similar methodology of NU as
where \(G = {\xi _f}{\beta ^2}{\left( {{{\mathbf {a}}^T}{\mathbf {c}}} \right) ^2}\), \(F = {\xi _n}{\beta ^2}{\left( {{{\mathbf {a}}^T}{\mathbf {c}}} \right) ^2}\). The means of G, GF and \({{G^2}}\) are, respectively, given by
Substitute Eqs. (16)–(20) into Eq. (11), we obtain the EC expression of FU with low SNR approximation.
Remark 2
It can be seen from the second-order Taylor expansion of low SNR that: (1) The EC is the sum of power functions related to the transmission SNR. (2) When the power allocation coefficient increases, the EC of NU increases.
4 Results and discussion
In this section, numerical analysis is provided to verify the accuracy of the analysis results for the considered system. In the case of a random channel, we implement the generation of Rayleigh random variables in \({10^5}\). We set the parameters as follows: bandwidth \(B = 1\), variance of system noise \({\sigma ^2} = 1\), reflection amplitude coefficient \(\beta = 1\). The purpose is to see the influence of the transmitted power and the number of RIS on the EC of the system. For power allocation factor of NOMA, we set \({{\xi _f}}=0.9\), \({{\xi _n}}=0.1\). Unless other stated, the parameter settings for numerical results used in this simulation are listed in Table 1.
As shown in Fig. 2, it illustrates the effect of SNR on the EC of NU and FU with the Monte Carlo results, respectively. The behavior of ECs becomes tight when SNR increases based on Eqs. (9) and (10), this is because high SNR approximation is used in the derivation. The simulation results show that the EC of NU increases linearly with the increase in SNR. But as SNR value increases, the theoretical EC of FU increases slowly and converges to a ceiling because FU suffers from NU’s interference when it detects its own signals. The approximation of EC is a constant as we analyzed in Remark 1. In addition, it is clear to see the important influence of the number of RIS elements N on the EC when applying \(N = 1, 3, 5\). That is the EC certainly increases as the number of RIS elements N increases, which is consistent with the result in [44].
Figures 3 and 4 plot the relationship ECs versus SNR in the case of NOMA and OMA for the NU and FU, respectively. We can observe that the EC of NU for RIS-aided NOMA is superior to RIS-aided OMA. However, FU suffers from NU’s interference in NOMA is the reason why the EC of FU in OMA is better than that of NOMA. Hence, we conclude that RIS-aided NOMA can significantly improve the EC of NU but not FU. Moreover, in order to better analyze the EC of the whole system, the sum EC of RIS-aided NOMA and OMA are compared in Fig. 5 for different number of RIS elements. The simulations show that for the whole system, the EC is excellent when NOMA is applied. Thus it can be seen the sum EC is dominated by NU. Another observation is that the increase in the number of RIS elements N has a positive effect on the sum EC of the system.
To exhibit the impact of low SNR on the EC, the approximate behavior of the EC in the case of low SNR is shown in Fig. 6. We take the SNR from \(-\)25 to \(-\)10 dB and the number of RIS elements \(N = 3\) as an example. The low SNR approximation of NU, FU and the sum EC of the system is compared. The good match between the approximation and the simulation in low SNR condition confirms the derived expressions. Besides, the result shows that the EC increases exponentially as SNR increasing in the condition of low SNR regions.
5 Conclusion
In this paper, we considered a downlink wireless communication system with RIS-aided NOMA technology. To consider delay-sensitive requirements, the EC as the evaluation metric was taken into account. First, we derived the approximate expressions for the EC of NU and FU. Through the simulation, the main influence factors of the EC were the number of RIS N, transmit power budget \({P_s}\) and QoS exponent \(\alpha\), as well as power allocation coefficients \({{\xi _n}}\), \({{\xi _f}}\) and bandwith B. In addition, we provided the relationship between ECs and SNR both for NOMA and OMA and concluded that the EC is excellent when applies NOMA for the whole system. Finally, the asymptotic expression of EC by invoking Taylor expansion at low SNR was given, which offers a theoretical basis for the actual deployment of the system.
To sum up, the wireless communication system combined RIS with NOMA has strong advantages and can meet the requirements of large-scale connection. Our work will provide some guidance for the design and performance evaluation for the future research works in the RIS-NOMA aspects.
Availability of data and materials
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Abbreviations
- 6G:
-
The sixth generation
- IoT:
-
Internet of things
- QoS:
-
Quality of service
- RIS:
-
Reconfigurable intelligent surface
- RF:
-
Radio frequency
- mmWave:
-
Millimeter-wave
- MIMO:
-
Multiple-input multiple-output
- SWIPT:
-
Simultaneous wireless information and power transfer
- NOMA:
-
Non-orthogonal multiple access
- B5G:
-
the beyond fifth generation
- SIC:
-
Serial interference cancellation
- EC:
-
Effective capacity
- MISO:
-
Multi-input single-output
- TAS:
-
Transmit antenna selection
- SNR:
-
Signal-to-noise ratio
- OMA:
-
Orthogonal multiple access
- PDF:
-
Probability density function
- S:
-
Source
- NU:
-
Near user
- FU:
-
Far user
- AWGN:
-
Additive white Gaussian noise
- SINR:
-
Signal-to-interference-plus-noise-ratio
- CSI:
-
Channel status information
References
G. Liu, Y. Huang, N. Li, J. Dong, J. Jin, Q. Wang, N. Li, Vision, requirements and network architecture of 6G mobile network beyond 2030. China Commun. 17, 92–104 (2020)
W. Saad, M. Bennis, M. Chen, A vision of 6G wireless systems: applications, trends, technologies, and open research problems. IEEE Netw. 34, 134–142 (2020)
C.-X. Wang, J. Huang, H. Wang, X. Gao, X.You, Y.Hao, 6G wireless channel measurements and models: trends and challenges. IEEE Veh. Technol. Mag. 15, 22–32 (2020)
A. Benjebbour, Y. Saito, Y. Kishiyama, A. Li, A. Harada, T. Nakamura, Concept and practical considerations of non-orthogonal multiple access (NOMA) for future radio access, in International Symposium on Intelligent Signal Processing and Communication Systems, 12–15 Nov 2013, Okinawa (2013), pp. 770–774
Y. Xu, G. Gui, H. Gacanin, F. Adachi, A survey on resource allocation for 5G heterogeneous networks: current research, future trends, and challenges. IEEE Commun. Surv. Tutor. 23, 668–695 (2021)
Y. Guo, Z. Zhao, K. He, S. Lai, J. Xia, L. Fan, Efficient and flexible management for industrial internet of things: a federated learning approach. Comput. Netw. 192, 108122 (2021)
C. Yao, Y. Liu, X. Wei, G. Wang, F. Gao, Backscatter technologies and the future of internet of things: challenges and opportunities. Intell. Converg. Netw. 1, 170–180 (2020)
M. Di Renzo, A. Zappone, M. Debbah, M.-S. Alouini, C. Yuen, J. de Rosny, S. Tretyakov, Smart radio environments empowered by reconfigurable intelligent surfaces: how it works, state of research, and the road ahead. IEEE J. Sel. Areas Commun. 58, 2450–2525 (2020)
Q. Wu, R. Zhang, Towards smart and reconfigurable environment: intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 58, 106–112 (2020)
S. Gong, X. Lu, D.T. Hoang, D. Niyato, L. Shu, D.I. Kim, Y.-C. Liang, Toward smart wireless communications via intelligent reflecting surfaces: a contemporary survey. IEEE Commun. Surv. Tutor. 22, 2283–2314 (2020)
T. Bai, C. Pan, Y. Deng, M. Elkashlan, A. Nallanathan, L. Hanzo, Latency minimization for intelligent reflecting surface aided mobile edge computing. IEEE J. Sel. Areas Commun. 38, 2666–2682 (2020)
Y. Liu, X. Liu, X. Mu, T. Hou, J. Xu, M. Di Renzo, N. Al-Dhahir, Reconfigurable intelligent surfaces: principles and opportunities. IEEE Commun. Surv. Tutor. 1–1 (2021)
C. Huang, A. Zappone, G.C. Alexandropoulos, M. Debbah, C. Yuen, Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 18, 4157–4170 (2019)
Y. Xu, Z. Gao, Wang, Z., Huang, C., Yang, Z., Yuen, C.: RIS-Enhanced WPCNs: Joint radio resource allocation and passive beamforming optimization. IEEE Trans. Veh. Technol, 70, 7980–7991 (2021)
Z. Gao, Y. Xu, Q. Wang, Q. Wu, D. Li, Outage-constrained energy efficiency maximization for RIS-assisted WPCNs. IEEE Commun. Lett. 1–1 (2021)
Q. Wu, R. Zhang, Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wirel. Commun. 18, 5394–5409 (2019)
M. Jung, W. Saad, Y. Jang, G. Kong, S. Choi, Reliability analysis of large intelligent surfaces (LISs): rate distribution and outage probability. IEEE Wirel. Commun. Lett. 8, 1662–1666 (2019)
S. Hu, F. Rusek, O. Edfors, Capacity degradation with modeling hardware impairment in large intelligent surface, in IEEE Global Communications Conference (GLOBECOM), 09–13 Dec 2020; United Arab Emirates (2018), pp. 1–6
J. He, M. Leinonen, H. Wymeersch, M. Juntti, Channel estimation for RIS-aided mmWave MIMO systems, in IEEE Global Communications Conference–GLOBECOM 2020, pp. 7–11 Dec 2020, Taiwan (2020), pp. 1–6
J. He, H. Wymeersch, T. Sanguanpuak, O. Silven, M. Juntti, Adaptive beamforming design for mmWave RIS-aided joint localization and communication, in IEEE Wireless Communications and Networking Conference Workshops (WCNCW), 6–10 Apr 2020, Seoul (2020), pp. 1–6
Zhiguo Ding, Vincent H. Poor, A simple design of IRS-NOMA transmission. IEEE Commun. Lett. 24, 1119–1123 (2020)
Ming Zeng, Xingwang Li, Gen Li, Wanming Hao, Octavia A. Dobre, Sum rate maximization for IRS-assisted uplink NOMA. IEEE Commun. Lett. 25, 234–238 (2021)
X. Li, Y. Zheng, M.D. Alshehri, L. Hai, V. Balasubramanian, M. Zeng, G. Nie, Cognitive AmBC-NOMA IoV-MTS networks with IQI: Reliability and security analysis. IEEE Trans. Intell. Transp. Syst., 1–12 (2021)
X. Li, J. Li, Y.i Liu, Z. Ding, A. Nallanathan, Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Trans. Wirel. Commun. 19, 680–695 (2020)
X. Li, M. Zhao, M. Zeng, S. Mumtaz, V. G. Menon, Z. Ding, O. A. Dobre, Hardware impaired ambient backscatter NOMA system: reliability and security. IEEE Trans. Commun. 69, 2723–2736 (2021)
Y. Xu, G. Gui, H. Gacanin, F.Adachi, A survey on resource allocation for 5G heterogeneous networks: current research, future trends, and challenges. IEEE Commun. Surv. Tutor. 23, 668–695 (2021)
X. Li, J. Li, Y. Liu, Z. Ding, A. Nallanathan, Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Trans. Wirel. Commun. 19, 680–695 (2020)
Z. Ding, Y. Liu, J. Choi, Q. Sun, M. Elkashlan, I. Chih-Lin, H.V. Poor, Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Commun. Mag. 55, 185–191 (2017)
Z. Ding, Z. Yang, P. Fan, H.V. Poor, On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Process. Lett. 21, 1501–1505 (2014)
B. Zheng, Q. Wu, R. Zhang, Intelligent reflecting surface-assisted multiple access with user pairing: NOMA or OMA? IEEE Commun. Lett. 24, 753–757 (2020)
Z. Ding, R. Schober, H.V. Poor, On the impact of phase shifting designs on IRS-NOMA. IEEE Wirel. Commun. Lett. 9, 1596–1600 (2020)
Z. Zhang, C. Zhang, C. Jiang, F. Jia, J. Ge, F. Gong, Improving physical layer security for reconfigurable intelligent surface aided NOMA 6G networks. IEEE Trans. Veh. Technol. 70, 4451–4463 (2021)
A. Hemanth, K. Umamaheswari, A.C. Pogaku, D.-T. Do, B.M. Lee, Outage performance analysis of reconfigurable intelligent surfaces-aided NOMA under presence of hardware impairment. IEEE Access 8, 212156–212165 (2020)
Q. Chen, M. Li, X. Yang, R. Alturki, M.D. Alshehri, F. Khan, Impact of residual hardware impairment on the IoT secrecy performance of RIS-Assisted NOMA networks. IEEE Access 9, 42583–42592 (2021)
D. Wu, R. Negi, Effective capacity: a wireless link model for support of quality of service. IEEE Trans. Wirel. Commun. 2, 630–643 (2003)
M. You, H. Sun, J. Jiang, J. Zhang, Unified framework for the effective rate analysis of wireless communication systems over MISO fading channels. IEEE Trans. Commun. 65, 1775–1785 (2017)
Y.H. Al-Badarneh, C.N. Georghiades, C.E. Mejia, On the effective rate of MISO/TAS systems in rayleigh fading, in IEEE International Symposium on Information Theory (ISIT), 25–30 June 2017, Aachen (2017), pp. 2328–2332
X. Li, J. Li, L. Li, J. Jin, J. Zhang, D. Zhang, Effective rate of MISO systems over ?–µ shadowed fading channels. IEEE Access 5, 10605–10611 (2017)
M. Matthaiou, G.C. Alexandropoulos, H.Q. Ngo, E.G. Larsson, Effective rate analysis of MISO Rician fading channels, in IEEE 7th Sensor Array and Multichannel Signal Processing Workshop (SAM) (2012), pp. 53–56
Minglei You, Hongjian Sun, Jing Jiang, Jiayi Zhang, Effective rate analysis in Weibull fading channels. IEEE Wirel. Commun. Lett. 5, 340–343 (2016)
T. Hou, Y. Liu, Z. Song, X. Sun, Y. Chen, L. Hanzo, Reconfigurable intelligent surface aided NOMA networks. IEEE J. Sel. Areas Commun. 38, 2575–2588 (2020)
H. Liu, H. Ding, L. Xiang, J. Yuan, L. Zheng, Outage and BER performance analysis of cascade channel in relay networks, in The 9th International Conference on Future Networks and Communications (FNC-2014), 17–20 Aug 2014, Niagara Falls (2014), pp. 23–30
I.S. Gradshteyn, I.M. Ryzhik, Table of Integrals, Series, and Products, 7th ed., San Diego (2007), p. 676
B. He, A. Liu, N. Yang and V. K. N. Lau, On the design of secure non-orthogonal multiple access systems. IEEE J. Sel. Areas Commun. 35, 2196–2206 (2017)
J. Choi, Effective capacity of NOMA and a suboptimal power control policy with delay QoS. IEEE Trans. Commun. 65, 1849–1858 (2017)
L. Kong, Y. Ai, S. Chatzinotas and B. Ottersten, Effective rate evaluation of RIS-Assisted communications using the sums of cascaded α-μ random variates. IEEE Access 9, 5832–5844 (2021)
Acknowledgements
Not applicable.
Funding
This work was supported in party by Henan Scientific and Technological Research Project under Grant 212102210557, in part by Key Scientific Research Projects of Higher Education Institutions in Henan Province under Grant 20A510007, and in part by the National Natural Science Foundation of China under Grant 61601414.
Author information
Authors and Affiliations
Contributions
GL, GH and XL propose the innovation ideals. HL and XL carry out the experiments. HL carries out the original draft. GL, HL, GH, XL, BR and FK review the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Appendix 1: Proof of Theorem 1
Let’s express \({{\mathbf {h}}}_{\mathrm{sr}}\), \({{\mathbf {h}}}_{\mathrm{rn}}\) and \({{\mathbf {h}}}_{\mathrm{rf}}\) in the form of \({{\mathbf {h}}}_{\mathrm{sr}} = {\mathbf {a}}{e^{j{\mu _m}}}\), \({{\mathbf {h}}}_{\mathrm{rn}} = {\mathbf {b}}{e^{j{\nu _m}}}\) and \({{\mathbf {h}}}_{\mathrm{rf}} = {\mathbf {c}}{e^{j{\lambda _m}}}\), where \({\mathbf {a}} = \left( {{a_1},...,{a_n},...,{a_N}} \right)\), \({\mathbf {b}} = \left( {{b_1},...,{b_n},...,{b_N}} \right)\), \({\mathbf {c}} = \left( {{c_1},...,{c_n},...,{c_N}} \right)\), and variances are \(\sigma _a^2\), \(\sigma _b^2\), and \(\sigma _c^2\), respectively. In this paper, we assume there are no phase shift errors, that is to say: \({\theta _m} = - {\mu _m} - {\nu _m}\) and \({\theta _m} = - {\mu _m} - {\lambda _m}\). So we can rewrite the SNR of NU is rewritten as
By applying [45], let \(U \buildrel \Delta \over = {{\mathbf {a}}^T}{\mathbf {b}}\), we can give the PDF for U:
According to probability theory, we can get the PDF of \(X = {U^2}\)
Based on the definition of the EC in Eq. (8), we can write the expression of the EC at NU as
According to the definition of expectation in probability knowledge, \(E\left( {{e^{{{-}}\alpha B{{\log }_2}\left( {1 + {\gamma _n}} \right) }}} \right)\) is written as
where \(\delta = \frac{{{\xi _n}{P_s}{\beta ^2}}}{{{\sigma ^2}}}\). Then we replace Eq. (23) to Eq. (25), we have
In fact, \(\delta\) term is a variate which is quite greater than 1, x is a number from zero to infinity. When \(\delta \rightarrow \infty\), we have the following approximation \(1 + \delta {{x}} \approx \delta {{x}}\), based on the above discussion, Eq. (26) is written as
We can rewrite \({{{e}}^{ - \alpha B{{\log }_2}\left( {\delta {{x}}} \right) }}\) as \({\left( {\delta {{x}}} \right) ^{ - \frac{{\alpha B}}{{\ln (2)}}}}\) by the exponential algorithm. Now, using [46], Eq. (6.561.16)], Eq. (27) is written as
Finally, substituting Eq. (28) for Eq. (24), we can get the EC of NU, as is showed in Eq. (9). So, the proof is completed.
Appendix 2: Proof of Theorem 2
Similar to NU, the SNR of FU as
The same, we can get the PDF of \(V = {\left| {{{\mathbf {a}}^T}{\mathbf {c}}} \right| ^2}\)
The expression of the EC of FU as
Then, \(E\left( {{e^{{{-}}\alpha B{{\log }_2}\left( {1 + {\gamma _f}} \right) }}} \right)\) is written as
For \({\left( {\frac{{{\xi _f}{P_s}{\beta ^2}y}}{{{\sigma ^2} + {P_s}{\beta ^2}{\xi _n}y}}} \right) ^{^{ - \frac{{\alpha B}}{{\ln (2)}}}}}\), y is a number from zero to infinity, when \({{y}} \rightarrow \infty\), we have the following approximation \({\left( {\frac{{{\xi _f}{P_s}{\beta ^2}y}}{{{\sigma ^2} + {P_s}{\beta ^2}{\xi _n}y}}} \right) ^{^{ - \frac{{\alpha B}}{{\ln (2)}}}}} \approx {\left( {\frac{{{\xi _f}y}}{{{\xi _n}y}}} \right) ^{^{ - \frac{{\alpha B}}{{\ln (2)}}}}}\). And then use the same calculation as NU, we can get the EC at FU, as is showed in Eq. (10) finally. The proof is completed.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, G., Liu, H., Huang, G. et al. Effective capacity analysis of reconfigurable intelligent surfaces aided NOMA network. J Wireless Com Network 2021, 198 (2021). https://doi.org/10.1186/s13638-021-02070-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-021-02070-7