1 Introduction

Non-orthogonal multiple access (NOMA) has recently been shown as one of the potential candidates for 5G and beyond based wireless networks to overcome the limitations of the current technologies such as energy efficiency, latency and user fairness [1,2,3]. One of the critical features of NOMA techniques is that multiple users are permitted to use the same resources in time, frequency and/or code domain [4]. It means that a strong user, i.e. a NU, is given a lower power allocation factor than a weak user, i.e. a FU, to ensure user fairness [1, 5,6,7]. Two key techniques applied in NOMA consist of superposition coding (SC) [2] and successive interference cancellation (SIC) [1, 2]. As an extended version of NOMA, cooperative NOMA (C-NOMA) [8, 9] exploits a user with better channel conditions, namely a relaying user, to assist to forward the information to another user with poor channel conditions. Therefore, it can increase the coverage region of BS and improve the performance of NOMA systems.

Radio frequency (RF) based energy harvesting (EH) can help solve energy constraint issues in mobile devices, wireless sensors as well as the relaying-acted nodes of wireless communication networks [10, 11]. At relay nodes, the energy harvesting is normally performed in the first phase of signal transmitting time block. This harvested energy is dedicated for: i) consuming at the relay and ii) forwarding the decoded information to the destination.

The combination of simultaneous wireless information and power transfer (SWIPT) and C-NOMA in 5G systems has demonstrated an outperformed energy efficiency and coverage area over OMA [7, 12]. More, by forwarding the information to far users, the relay based SWIPT C-NOMA can improve the integrity and reliability of the transmitted data for weak users [13]. Power-splitting protocol (PSR) and time-switching protocol (TSR) are exploited at SWIPT based relaying nodes to harvest energy and process information [5, 6, 14, 15]. In [16], the sum throughput of users in SWIPT based C-NOMA system was studied. Closed-form and closed-form approximate expressions of outage probability were achieved. In [17], two protocols based on SWIPT, namely CNOMA-SWIPT-PS and CNOMA-SWIPT-TS, were proposed. The effectiveness of the proposed schemes was demonstrated over OMA and the work in [18]. In [19], a SWIPT based C-NOMA system was investigated. A joint design for the power allocation coefficients and the PS factor was proposed to improve the system performance. The derivation of analytical expressions for the outage probabilities of near and far users was also provided. In [20], a PSR based SWIPT for C-NOMA was studied. Compared to the protocol in [21], this protocol can considerably reduce the outage probability of the strong users and increase the system throughput. In [22], the outage probability and throughput of the proposed TSR protocol was superior to the normal TSR protocol.

There are two main data forwarding schemes in relay-assisted C-NOMA, including decode-and-forward (DF) and amplify-and-forward (AF) [1]. Furthermore, in relay based C-NOMA, far users normally receive the transmitted signal which is forwarded from relay nodes [23,24,25,26,27]. This is because there are some obstacles on the propagation [5, 6, 28]. However, in system models without obstacle, these far users can receive signals from both relay and BS, namely therefore relay based C-NOMA with direct links [25, 29,30,31]. In [29], a dynamic DF based C-NOMA scheme for downlink transmission was proposed. The outage probability of the proposed scheme was derived by applying point process theory. In [32], three cooperative relaying schemes were proposed in a DF based C-NOMA system. The system performance for the proposed schemes was superior to the cooperative DF relaying without direct links and multiple user superposition transmission without relaying. In [33], a DF relay aimed C-NOMA system with direct link between BS and weak user was studied. In [34], a system cooperative device-to-device systems with NOMA in which the BS can communicate simultaneously with all users was considered. Two decoding strategies, namely single signal decoding scheme and maximum ratio combining (MRC) decoding scheme, were proposed. The numerical results showed that the ergodic sum rate as well as outage probability achieve better than the conventional NOMA schemes. The authors in [35] proposed a protocol to permit the BS to adaptively switch between direct and indirect modes in C-NOMA system with two users. The analytical results demonstrated that the proposed protocol overwhelmed the conventional C-NOMA protocol. In [36], the outage performance of dual DF based SWIPT NOMA system with direct link was presented.

The use of relays for forwarding information from sources to destinations and harvesting RF energy has been investigated in the current technologies such as OFDMA, SWIPT/WPT [37,38,39]. In [37], a relaying selection scheme, namely OFDMA relaying selection, was proposed for OFDM multihop cooperative networks with L relays and M hops (\(M,\,L\ge 2\)). The end-to-end outage performance of the proposed approach was evaluated and compared to that of the OFDM relaying selection approach. In [38], a relaying selection scheme was investigated in a two-hop relay-assisted multi-user OFDMA network with K fixed relays and L users (\(2\le L\le K\)), where the end-nodes exploited the SWIPT mechanism based on the power splitting (PS) technique. This relaying selection is to optimize the PS ratio of the end nodes as well as the relay, carrier, and power assignment so that the sum-rate of the system was maximized under the harvested energy and transmitted power constraints. In [39], a survey of the SWIPT and WPT assisted energy harvesting techniques was presented. The survey provided a detailed description of various potential emerging technologies for the fifth generation (5G) communications with SWIPT/WPT.

In this paper, we investigate a wireless communication system model which can ensure the user fairness by allocating power and harvest the RF energy from the source, namely C-NOMA based system model. We combine SWIPT and C-NOMA in our model system to study its performance metric in terms of the outage probability, throughput and energy efficiency. The investigated model consists one base station and two users where one user acts as a relaying user, another user is a FU. The BS simultaneously broadcasts the superposed coding signals to both users and thus the FU also receives the signal from BS. Based on NOMA mechanism, the FU with poor channel conditions is allocated more power than the NU with strong channel conditions. Moreover, the SIC process is performed at the NU which acts as the relaying user. After receiving the transmitted signal, the relaying user decodes the FU\(^{'}\)s signal and its own signal utilizing SIC. The decoded signal of the FU at the relaying user is then forwarded to the FU using DF protocol. The relaying user employs PSR protocol in its communication process. Involving in signal processing at relay node, delay limited transmission (DLT) and delay tolerant transmission (DTT) modes can be exploited at this node [14]. The DLT mode refers to the block wise received signal decoding mechanism at the destination node while the DTT mode refers to the storage of the received data block in the buffer of the destination node prior to data decoding. The key contributions of our work in this paper are sumarized as follows:

  • Closed-form expressions of the performance, i.e., outage probability, throughput, ergodic rate and EE, are derived for the PSR protocol with DLT and DTT modes and direct link. This performance of the system model with direct link is compared to that for C-NOMA without direct link as well as OMA. The simulation results show that the C-NOMA with direct link achieves a better performance than that for the C-NOMA without direct link and OMA.

  • The impacts of above mentioned parameters on the direct link are evaluated via the numerical simulation results to realize the changes of the performance. These impacts are as a background for choosing the suitable values of the parameters for system model to achieve the tradeoff among terms of the performance as well as users.

The rest of paper is organized as follows. Section 2 presents the detail of the proposed system model and assumptions. Section 3 analyzes the performance parameters including outage probability, throughput, ergodic rate and EE. Section 4 discusses the simulation results. Finally, Sect. 5 gives the main conclusions.

2 Methods

In this section, we investigate the combination of the C-NOMA based system model and PSR based SWIPT technique. From the system model, we analyze and derive the performance metric in terms of outage probability, throughput, ergodic rate, and energy efficiency under constraints of direct and relay links among source, destination, and relay. We then utilize the Monte Carlo numerical approach to simulate and verify the analytical results. Furthermore, the performance metric is compared between CNOMA and OMA schemes, a direct link and relay link to clarify which scheme is superior.

2.1 System model

Fig. 1
figure 1

System Model

Full size image

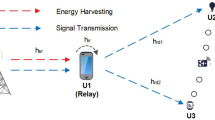
Figure 1 describes the model system with one source S and two users \(D_{1}\) and \(D_{2}\). These two users receive the transmitted signal from the source S. Because \(D_{2}\) is far from S, so \(D_{1}\) also helps S forward the information to \(D_{2}\). According to [40], the BS first broadcasts a threshold signal to all users in its coverage. One bit, i.e., 0 or 1, is used by the users to give the feedbacks of their received signal strength to the BS by comparing its own signal to the threshold signal. The threshold value therefore needs to be chosen carefully. In [41], optional thresholds for systems with different power constraints were also developed. After receiving the feedback bits from the users, the BS decides which user is a strong or weak user and sends this information to the users. In this model, the energy is harvested from the RF signal received at the relay. The harvested energy is stored in the battery which is a finite energy source. A part of this energy is used for the operation of the relay, while the remaining part is stored in the battery. It is assumed that the capacity of the battery is finite. Specifically, to maintain the operation, \(D_1\) harvests the energy from S by employing the PSR protocol, while the DF scheme is employed to decode and forward the information from S to \(D_2\). This system model can also be applied in wireless sensor and mobile networks where the nodes and/or users experience urban with high buildings e.g., some system models in [42,43,44,45,46,47].

2.2 Energy harvesting and data transmission protocol

Fig. 2
figure 2

Energy harvesting and data transmission protocol

Full size image

Figure 2 shows the power splitting (PS) protocol for EH and IP. Specifically, in the first T/2, S sends data to both \(D_{1}\) and \(D_{2}\) and \(D_{1}\) harvests the energy from S with a part of the received signal power of \(\beta {P_S}\). Because the data is already sent to \(D_{2}\) in the first T/2, it is not necessary to resend the same information to \(D_{2}\) in the second time slot, unless S wants to send new information but it is beyond the scope of this work. In other words, \(D_{2}\) only decodes the information from \(D_{1}\) with a part of the remaining signal power of \(\left( {1-\beta }\right) {P_S}\) in the second time slot and employs MRC with the one received from S in the first time slot.

Table 1 lists the definition of the parameters used in the model and through the paper.

Table 1 Symbol definition
Full size table

2.2.1 Energy harvesting at \(D_{1}\)

We know that the amount of harvested energy from RF signal is small. However, the main power of the relay is the battery and the harvested energy is stored in the battery. Following the same approach as in [48], in this paper, we assumed that \(D_{1}\) uses the total harvested energy to relay its detected message of \(D_{2}\) and this harvested energy is sufficient for data transmission and processing.

The observation at \(D_{1}\) is determined based on SC as follows

$$\begin{aligned} {y_{{D_1}}} = {h_1}(\sqrt{{\alpha _1}{P_S}} {x_1} + \sqrt{{\alpha _2}{P_S}} {x_2}) + {n_{{D_1}}}, \end{aligned}$$
(1)

The assumptions are given that \(E[{x_1^2}] = E[{x_2^2}] = 1\), and, without loss of generality, \({\alpha _2}>{\alpha _1}>0\) satisfying \({\alpha _1}+{\alpha _2}=\)1.

As shown in Fig 2, \(D_1\) only harvests the energy from S during the first T/2. The harvested energy at \(D_1\) is thus computed by

$$\begin{aligned} {E_H} = \beta \eta {\left| {{h_1}} \right| ^2}\rho \left( {T/2} \right) , \end{aligned}$$
(2)

From (2), we understand that the operation of the energy harvesters can occur in the non-linear region. Several works have also investigated the non-linearity of practical energy harvesting circuit [49, 50]. However, to overcome this challenge in our work for practical problems as well as to scope with our study, several EH circuits can be placed in parallel to yield a sufficiently large linear conversion region [51, 52].

The harvested energy is dissipated at \(D_1\) and used to forward the decoded data to \(D_2\). The transmitted power at \(D_1\) obtaining from the harvest energy EH is determined by

$$\begin{aligned} {P_r} = \frac{{{E_H}}}{{\left( {T/2} \right) }} = \frac{{\beta \eta {{\left| {{h_1}} \right| }^2}\rho \left( {T/2} \right) }}{{\left( {T/2} \right) }} = \beta \eta {\left| {{h_1}} \right| ^2}\rho . \end{aligned}$$
(3)

We can see that Eqs. (2) and (3) represent for linear energy harvesting circuits. However, as mentioned above, the non-linear region can appear in the operation of the energy harvester. Various studies in the recent trends have also emphasized on the linear architecture of the energy harvester [43, 44]. Therefore, to solve the nonlinear issue of the EH circuits based on linear region, we can yield a sufficiently large linear conversion region via parallel EH circuits.

2.2.2 Information processing at \(D_1\) and \(D_2\)

In fact, the NOMA scheme is only enabled when the strong/weak users can be identified. Hence, channel state information (CSI) of the links from S to \(D_{1}\) and from \(D_{1}\) to \(D_{2}\) is critical. In order to share these CSI, there are different approaches [53, 54], among which a typical one is to use pilot sequences.

Based on NOMA principle, \(D_{2}\) is allocated more power than \(D_{1}\). By applying SIC [14], \(D_{1}\) decodes both signal \(x_{2}\) and its own signal \(x_{1}\). It is assumed that the SIC is perfect. From (1), the received signal to interference plus noise ratio (SINR) at \(D_{1}\) to detect \(x_{2}\) of \(D_{2}\) is determined by

$$\begin{aligned} {\gamma _{2,{D_1}}} = \frac{{{\psi _I}{{\left| {{h_1}} \right| }^2}{\alpha _2}\rho }}{{{\psi _I}{{\left| {{h_1}} \right| }^2}{\alpha _1}\rho + 1}}. \end{aligned}$$
(4)

The interference is not in the received signal at \(D_1\) after SIC process. Therefore, the received SNR at \(D_{1}\) to detect its own message \(x_{1}\) is given by

$$\begin{aligned} {\gamma _{1,{D_1}}} = {\psi _I}{\left| {{h_1}} \right| ^2}{\alpha _1}\rho . \end{aligned}$$
(5)

Over direct link, the signal at \(D_{2}\) is given by

$$\begin{aligned} {y_{{1,D_2}}} = {h_0}(\sqrt{{\alpha _1}{P_S}} {x_1} + \sqrt{{\alpha _2}{P_S}} {x_2}) + {n_{{D_2}}}. \end{aligned}$$
(6)

Therefore, the received SINR at \(D_{2}\) to detect \(x_2\) for the direct link is given by

$$\begin{aligned} {\gamma _{1,{D_2}}} = \frac{{{{\left| {{h_0}} \right| }^2}{\alpha _2}\rho }}{{{{\left| {{h_0}} \right| }^2}{\alpha _1}\rho + 1}}. \end{aligned}$$
(7)

Over the relaying link, the decoded signal \(x_2\) at \(D_1\) is forwarded to \(D_{2}\). Thus, the received signal at \(D_{2}\) can be expressed as

$$\begin{aligned} {y_{{2,D_2}}} = \left( {\sqrt{{P_r}} {x_2}} \right) {h_2} + n_{D_2}. \end{aligned}$$
(8)

Substituting Eq. (3) into Eq. (8), we obtain

$$\begin{aligned} {y_{{2,D_2}}} = \left( {\sqrt{\beta \eta \rho } } \right) \left| {{h_1}} \right| {h_2}{x_2} + {n_{{D_2}}}. \end{aligned}$$
(9)

The received SNR at \(D_2\) over the relaying link is thus expressed by

$$\begin{aligned} {\gamma _{2,{D_2}}} = {\left| {{h_2}} \right| ^2}{\left| {{h_1}} \right| ^2}{\psi _E}\rho . \end{aligned}$$
(10)

At \(D_{2}\), the signals from both relaying and direct links are combined by employing the MRC mechanism. The combined SINR can be obtained by

$$\begin{aligned} \gamma _{{D_2}}^{MRC} = {\left| {{h_1}} \right| ^2}{\left| {{h_2}} \right| ^2}\psi _{E}\rho + \frac{{{{\left| {{h_0}} \right| }^2}{\alpha _2}\rho }}{{{{\left| {{h_0}} \right| }^2}{\alpha _1}\rho + 1}}. \end{aligned}$$
(11)

3 Performance Analysis

This section presents the analysis of the performance of the system model in which closed-form expressions of the outage probability, throughput, ergodic rate and EE are determined in DTT and DLT modes.

3.1 Outage performance

3.1.1 Outage probability at \(D_{1}\)

User \(D_1\) is not in outage when it can decode both signals \(x_1\) and \(x_2\) received from the BS. The outage probability at \(D_1\) is thus obtained by

$$\begin{aligned} P_{D_1} = 1 - \Pr \left( {{\gamma _{2,{D_1}}}> \gamma _{t{h_2}},{} {\gamma _{1,{D_1}}} > \gamma _{t{h_1}}} \right) , \end{aligned}$$
(12)

where, \(\gamma _{t{h_1}} = {2^{2{R_1}}} - 1\) and \(\gamma _{t{h_2}} = {2^{2{R_2}}} - 1\) represent the threshold SNRs at \(D_{1}\) for detecting signals \(x_1\) and \(x_2\), respectively.

Theorem 1

The outage probability at \(D_{1}\) is given by

$$\begin{aligned} P_{D1} = 1 - {e^{ - \frac{{{\theta _1}}}{{{\Omega _1}}}}}, \end{aligned}$$
(13)

where, \({\theta _1} = \max ({\tau _1},{\nu _1}),{\tau _1} = \frac{{\gamma _{th2}}}{{\rho {\psi _I}({\alpha _2} - {\alpha _1}\gamma _{th2})}}\) and \({\nu _1} = \frac{{\gamma _{th1}}}{{{a_1}{\psi _I}\rho }}\) with \({\alpha _2} > {\alpha _1}\gamma _{th2}.\)

Proof

From (12), the outage probability at \(D_{1}\) can be determined by

$$\begin{aligned} {P_{{D_1}}}&= {} 1\!-\!Pr\left( {\frac{{{\psi _I}{{\left| {{h_1}} \right| }^2}{\alpha _2}\rho }}{{{\psi _I}{{\left| {{h_1}} \right| }^2}{\alpha _1}\rho \!+\!1}}\!>\!{\gamma _{t{h_2}}},{} {} {} {} \psi _I{{\left| {{h_1}} \right| }^2}{\alpha _1}\rho \!>\! {\gamma _{t{h_1}}}} \right) \nonumber \\&= {} 1 - Pr\left( {{{\left| {{h_1}} \right| }^2}> \,\frac{{{\gamma _{t{h_2}}}}}{{\rho {\psi _I}\left( {{\alpha _2} - {\alpha _1}{\gamma _{t{h_2}}}} \right) }},\,\,{{\left| {{h_1}} \right| }^2} > \,\frac{{{\gamma _{t{h_1}}}}}{{{\alpha _1}\rho {\psi _I}}}} \right) \nonumber \\&= {} 1 - Pr({\left| {{h_1}} \right| ^2} \ge {\theta _1})\nonumber \\&= {} 1 - \int _{{\theta _1}}^\infty {{f_{{{\left| {{h_1}} \right| }^2}}}(x)dx} \end{aligned}$$
(14)

Applying the following equation

$$\begin{aligned} {f_{{h_i}}}(x) = \frac{1}{{{\Omega _i}}}\exp ( - \frac{x}{{{\Omega _i}}}),{} {} {} {} i \in \{ SD_{1},D_{1}D_{2}\mathrm{{\} }} \end{aligned}$$

Eq. (14) can be obtained as follows

$$\begin{aligned} {P_{{D_1}}}&= {} 1 - \int _{{\theta _{1}}}^\infty {\frac{1}{{{\Omega _1}}}{e^{\frac{{ - x}}{{{\Omega _1}}}}}dx}\nonumber \\&= {} 1 - {e^{ - \,\,\frac{{{\theta _{1}}}}{{{\Omega _1}}}}} \end{aligned}$$
(15)

The proof is completed. \(\square\)

Corollary 1

From (15), the outage probability at \(D_{1}\) for high SNR \(\rho \rightarrow \infty\) is expressed by

$$\begin{aligned} P_{D_1}^\infty = \frac{{{\theta _1}}}{{{\Omega _1}}} \end{aligned}$$
(16)

Proof

From (12), when \(\rho \rightarrow \infty\), the outage probability at \(D_{1}\) with \(1 - {e^{-x}} \approx x\) is given by

$$\begin{aligned} P_{D_1}^{\infty }&= {} 1 - {P_r}\left( {{{\left| {{h_1}} \right| }^2} \ge \theta _1} \right) \nonumber \\&= {} 1 - {e^{ - \frac{{\theta _1}}{{\Omega {\,_1}}}}}\nonumber \\&= {} \frac{{{\theta _1}}}{{{\Omega _1}}} \end{aligned}$$
(17)

The proof is completed. \(\square\)

Based on (15) and \({\alpha _2} > {\alpha _1}\gamma _{th2}\), \(P_{D_1}\) depends on \(\tau _{1}\) and the random variable \(\Omega _{1}\) (\(|h_1|^2\)). The closer the d, the lower the \(P_{D_1}\). This means that a better transmission quality can be achieved, and vice versa.

3.1.2 Outage probability at \(D_{2}\) for no direct link

Since \(D_1\) can not detect \(x_2\) as well as \(D_2\) can not recover the forwarded information from \(D_1\), the \(D_2\) is in outage. Hence, the outage probability at \(D_2\) is derived as (see (18)). By calculating \(J_2\) and \(J_3\), the outage probability for no direct link is determined by

$$\begin{aligned} \begin{array}{l} P_{{D_2},nodir} = \underbrace{\Pr \left( {{\gamma _{2,{D_1}}}< \gamma _{t{h_2}}^{HD}} \right) }_{{J_2}} + \underbrace{\Pr \left( {{\gamma _{2,{D_2}}} < \gamma _{t{h_2}}^{HD},{\gamma _{2,{D_1}}} > \gamma _{t{h_2}}^{HD}} \right) }_{{J_3}}, \end{array} \end{aligned}$$
(18)

Theorem 2

The outage probability at \(D_{2}\) can be obtained by

$$\begin{aligned} P_{{D_2},nodir} = 1 - {e^{ - \frac{{{\tau _1}}}{{{\Omega _1}}}}}+ \int \limits _{{\tau _1}}^\infty {\left( {1 - {{\mathop {e}\nolimits } ^{ - \frac{{\gamma _{t{h_2}}}}{{x{\psi _E}\rho {\Omega _2}}}}}} \right) \frac{1}{{{\Omega _1}}}\exp \left( {\frac{{- x}}{{{\Omega _1}}}} \right) } dx. \end{aligned}$$
(19)

Proof

Considering the Rayleigh fading channel, \(J_2\) can be given by

$$\begin{aligned} {J_2} = 1 - \exp \left( {\frac{{ - {\tau _1}}}{{{\Omega _1}}}} \right) . \end{aligned}$$
(20)

and \(J_3\) can be expressed as (see(21)).

$$\begin{aligned} \begin{array}{l} {J_3}=\Pr \left( {{{\left| {{h_2}} \right| }^2}{{\left| {{h_1}} \right| }^2}{\psi _E}\rho<\gamma _{t{h_2}},\frac{{{{\left| {{h_1}} \right| }^2}{\psi _I}{\alpha _2}\rho }}{{{\psi _I}{{\left| {{h_1}} \right| }^2}{\alpha _1}\rho +1}}>\gamma _{t{h_2}}} \right) \\ \\ \quad \,=\left\{ \begin{array}{l} \Pr \left( {{{\left| {{h_2}} \right| }^2}<\frac{{\gamma _{t{h_2}}}}{{{{\left| {{h_1}} \right| }^2}{\psi _E}\rho }}, {{\left| {{h_1}} \right| }^2}>\frac{{\gamma _{t{h_2}}}}{{{\psi _I}\rho \left( {{\alpha _2}-{\alpha _1}\gamma _{t{h_2}}} \right) }}} \right) ,{\alpha _2}> {\alpha _1}\gamma _{t{h_2}}\\ \\ 0,\,\,{\alpha _2} \le {a_1}\gamma _{t{h_2}} \end{array} \right. \\ \\ \quad \,= \int \limits _{\frac{{\gamma _{t{h_2}}}}{{{\psi _I}\rho \left( {{\alpha _2} - {\alpha _1}\gamma _{t{h_2}}} \right) }}}^\infty {\int \limits _0^{\frac{{\gamma _{t{h_2}}}}{{x{\psi _E}\rho }}} {{f_{{{\left| {{h_1}} \right| }^2}}}(x){f_{{{\left| {{h_2}} \right| }^2}}}(y)dxdy} }= \int \limits _{{\tau _1}}^\infty {\frac{1}{{{\Omega _{1}}}}\left[ {1 - \exp \left( {\frac{{ - \gamma _{t{h_2}}}}{{x{\psi _E}\rho {\Omega _{2}}}}} \right) } \right] \exp \left( {\frac{{ - x}}{{{\Omega _{1}}}}} \right) } dx. \end{array} \end{aligned}$$
(21)

The outage probability at \(D_2\) is given by

$$\begin{aligned} P_{{D_2},nodir} = \,{J_2}\, + \,{J_3}.\, \end{aligned}$$
(22)

\(\square\)

Corollary 2

The outage probability at \(D_{2}\) for high SNR can be determined as (see(23)), where \({K_1}(.)\) is the first order modified Bessel function of the second kind [55, Eq.(3.324.1)].

$$\begin{aligned} P_{{D_2},nodir}^{\infty }&= {} \Pr \left( {\frac{{{\alpha _2}}}{{{\alpha _1}}}< \gamma _{t{h_2}}} \right) + \Pr \left( {{{\left| {{h_2}} \right| }^2}< \frac{{\gamma _{t{h_2}}}}{{{\psi _E}\rho {{\left| {{h_1}} \right| }^2}}},\frac{{{\alpha _2}}}{{{\alpha _1}}}> \gamma _{t{h_2}}} \right) \nonumber \\&= {} \Pr \left( {{{\left| {{h_2}} \right| }^2} < \frac{{\gamma _{t{h_2}}}}{{{\psi _E}\rho {{\left| {{h_1}} \right| }^2}}},\frac{{{\alpha _2}}}{{{\alpha _1}}} > \gamma _{t{h_2}}} \right) \nonumber \\&= {} \int \limits _0^\infty {\left[ {1 - \exp \left( {\frac{{ - \gamma _{t{h_2}}}}{{{\psi _E}\rho {\Omega _2}x}}} \right) } \right] } \frac{1}{{{\Omega _1}}}\exp \left( {\frac{{ - x}}{{{\Omega _1}}}} \right) dx \nonumber \\&= {} 1 - 2\sqrt{\frac{{\gamma _{t{h_2}}}}{{{\psi _E}\rho {\Omega _1}{\Omega _2}}}} {K_1}\left( {2\sqrt{\frac{{\gamma _{t{h_2}}}}{{{\psi _E}\rho {\Omega _1}{\Omega _2}}}} } \right) . \end{aligned}$$
(23)

3.1.3 Outage probability at \(D_{2}\) for User Relaying with Direct Link

When \(x_{2}\) can be detected at \(D_{1}\) but the SINR is smaller than the target SNR after MRC or both \(D_{1}\) and \(D_{2}\) can not detect \(x_{2}\), the outage probability will occur at \(D_{2}\) and is given by (see(24))

$$\begin{aligned} {P_{{D_2},dir}} = \underbrace{{P_r} (\gamma _{{D_2}}^{MRC}< {\gamma _{th{{}_2}}})}_{{J_4}}\underbrace{{P_r}\left( {{\gamma _{2,{D_1}}} > {\gamma _{th{{}_2}}}} \right) }_{{J_5}} + {} \underbrace{{P_r}({\gamma _{2,{D_1}}}< {\gamma _{th{{}_2}}},{\gamma _{1,{D_2}}} < {\gamma _{th{{}_2}}})}_{{J_6}}, \end{aligned}$$
(24)

Theorem 3

The outage probability at \(D_{2}\) can be given by (see(25))

$$\begin{aligned} P_{{D_2},dir}&= {} \int _0^\infty {\int _0^{\psi _{I}\,{\tau _1}} {\frac{1}{{{\Omega _0}{\Omega _1}}}\left( {1-{e^{-\frac{{\gamma _{t{h_2}}}}{{x\psi _{E}\rho {\Omega _2}}}+\frac{{y{\alpha _2}}}{{x\psi _{E}{\Omega _2}\left( {y{\alpha _1}\rho +1} \right) }}}}} \right) {e^{-\frac{x}{{\Omega {_1}}}\!-\!\frac{y}{{{\Omega _0}}}}}dxdy}}\times {e^{ - \frac{{{\tau _1}}}{{{\Omega _1}}}}}\,\nonumber \\&+ \left( {1 - {e^{ - \frac{{\tau _1}}{{{\Omega _1}}}}}} \right) \left( {1 - {e^{ - \,\,\frac{{{\tau _1}\,\psi _{I}}}{{{\Omega _0}}}}}} \right) \end{aligned}$$
(25)

Proof

From (24), the outage probability at \(D_{2}\) is determined by (see(26)), (see(27)), (see(28))

$$\begin{aligned} {J_4}&= {} \Pr \left( {{{\left| {{h_2}} \right| }^2}< \frac{{\gamma _{t{h_2}}}}{{{{\left| {{h_1}} \right| }^2}\psi _{E}\rho }} - \frac{{{{\left| {{h_0}} \right| }^2}{\alpha _2}}}{{{{\left| {{h_1}} \right| }^2}\psi _{E}\left( {{{\left| {{h_0}} \right| }^2}{\alpha _1}\rho + 1} \right) }},{{\left| {{h_0}} \right| }^2} < {\tau _1}\,\psi _{I}} \right) \nonumber \\&= {} \int _0^\infty {\int _0^{\psi _{I}\,{\tau _1}} {\int \limits _0^{\frac{{\gamma _{t{h_2}}}}{{x\,\psi _{E}\rho }}\,\, - \,\,\frac{{y{\alpha _2}}}{{x\,\psi _{E}\left( {y\,{\alpha _1}\rho + 1} \right) }}} {{f_{{{\left| {h{\,_1}} \right| }^2}}}\left( x \right) {f_{{{\left| {{h_0}} \right| }^2}}}\left( y \right) {f_{{{\left| {h{\,_2}} \right| }^2}}}\left( z \right) dxdydz} } }\nonumber \\&= {} \int _0^\infty {\int _0^{\psi _{I}\,{\tau _1}} {\frac{1}{{{\Omega _0}{\Omega _1}}}\left( {1 - {e^{ - \,\,\frac{{\gamma _{t{h_2}}}}{{x\,\psi _{E}\rho \,\Omega {\,_2}}}\,\, + \,\,\frac{{y{\alpha _2}}}{{x\,\psi _{E}\Omega {\,_2}\left( {y\,{\alpha _1}\rho + 1} \right) }}}}} \right) {e^{ - \,\,\frac{x}{{\Omega {\,_1}}}\,\, - \,\,\frac{y}{{{\Omega _0}}}}}dxdy} } \end{aligned}$$
(26)
$$\begin{aligned} {J_5}&= {} {\left| {{h_1}} \right| ^2} > {\tau _1}=\int _{\tau _1}^\infty {{f_{{{\left| {h{\,_1}} \right| }^2}}}\left( x \right) dx}= {e^{ - \,\,\frac{{\tau _1}}{{\Omega {\,_1}}}}} \end{aligned}$$
(27)
$$\begin{aligned} {J_6}&= {} \Pr \left( {{{\left| {{h_0}} \right| }^2}< \psi _{I}{} {} {\tau _1},{{\left| {{h_1}} \right| }^2} < {\tau _1}} \right) = \int _0^{{\tau _1}} {\int _0^{\psi _{I}{} {\tau _1}} {{f_{{{\left| {h{{}_1}} \right| }^2}}}\left( x \right) } } {f_{{{\left| {{h_{{} 0}}} \right| }^2}}}\left( y \right) dxdy\;\;\;{} {} {} {} {} {}\nonumber \\&= {} \left( {1 - {e^{ - \frac{{\psi _{I}{} {\tau _1}}}{{{\Omega _0}}}}}} \right) \left( {1 - {e^{ - \frac{{{\tau _1}}}{{{\Omega _1}}}}}} \right) \end{aligned}$$
(28)

\(\square\)

3.2 Throughput for DLT mode

3.2.1 User relaying without direct link

With a given constant R, the transmitted information of the source node depends on the outage probability performance due to wireless fading channels. Therefore, the throughput of the system is determined by

$$\begin{aligned} \tau _{t,nodir} = \left( {1 - P_{{D_1}}} \right) {R_1} + \left( {1 - P_{{D_2},nodir}} \right) {R_2}, \end{aligned}$$
(29)

where \(P_{D_1}\) and \(P_{{D_2},nodir}\) can be achieved from (15) and (19), respectively.

3.2.2 User relaying with direct link

The throughput of system is given by

$$\begin{aligned} \tau _{t,dir} = \left( {1 - P_{{D_1}}} \right) {R_1} + \left( {1 - P_{{D_2},dir}} \right) {R_2}, \end{aligned}$$
(30)

where \(P_{{D_1}}\) and \(P_{{D_2},dir}\) can be achieved from (15) and (25), respectively.

3.3 Ergodic rate for DTT mode

3.3.1 Ergodic rate at \(D_{1}\)

The achievable rate at \(D_{1}\) where \(D_{1}\) can detect \(x_{2}\) is given by

$$\begin{aligned} {R_{{D_1}}} = \frac{1}{2}{\log _2}\left( {1 + {\gamma _{{D_1}}}} \right) . \end{aligned}$$
(31)

Theorem 4

The ergodic rate at \(D_{1}\) is determined by

$$\begin{aligned} R_{{D_1}} = \frac{{ - \exp \left( {\frac{1}{{{\psi _I}{\alpha _1}\rho {\Omega _1}}}} \right) }}{{2\ln 2}}Ei\left( {\frac{{ - 1}}{{{\psi _I}{\alpha _1}\rho {\Omega _1}}}} \right) , \end{aligned}$$
(32)

where Ei(.) indicates the exponential integral function [55, Eq.(3.354.4)].

Proof

See Appendix 1. \(\square\)

3.3.2 Ergodic rate at \(D_{2}\) for User Relaying Without Direct Link

Since \(x_2\) needs to be detected at both \(D_1\) and \(D_2\), the achievable rate at \(D_{2}\) is given by

$$\begin{aligned} {R_{{D_2},nodir}}{} = {} \frac{1}{2}{\log _2}\left( {1 + \min \left( {{\gamma _{2,{D_1}}},{\gamma _{2,{D_2}}}} \right) } \right) . \end{aligned}$$
(33)

Theorem 5

The ergodic rate at \(D_{2}\) is given by

$$\begin{aligned} R_{{D_2},nodir} = \frac{1}{{2\ln 2}}\int \limits _0^{\frac{{{\alpha _2}}}{{{\alpha _1}}}} {\left[ {\frac{{{e^{ - \frac{x}{{{\psi _I}\rho \left( {{\alpha _2} - {\alpha _1}x} \right) {\Omega _1}}}}}}}{{1 + x}}} \right. } \left. {+ \frac{{\int _{\frac{x}{{{\psi _I}\rho \left( {{\alpha _2} - {\alpha _1}x} \right) }}}^\infty {\frac{1}{{{\Omega _1}}}\left( {1 - {e^{ - \frac{x}{{y\rho {\psi _E}{\Omega _2}}}}}} \right) {e^{ - \frac{y}{{{\Omega _1}}}}}dy} }}{{1 + x}}} \right] dx. \end{aligned}$$
(34)

Proof

See Appendix 2 . \(\square\)

Remark 1

The ergodic rate in the asymptotic expression at \(D_{2}\) for high SNR region \(\rho \rightarrow \infty\) is obtained by

$$\begin{aligned} R_{{D_2},nodir}^{\infty }=\frac{1}{{2\ln 2}}\int \limits _0^\infty {\frac{{1 - {F_X}(x)}}{{1 + x}}dx}. \end{aligned}$$
(35)

From the analytical result in (35), this expression can be deployed by

$$\begin{aligned} R_{{D_2},nodir}^{\infty }\!=\!\frac{1}{{2\ln 2}}\!\int \limits _0^{\frac{{{\alpha _2}}}{{{\alpha _1}}}} {\frac{{\!2\sqrt{\!\frac{x}{{{\psi _E}\rho \,{\Omega _1}{\Omega _2}}}} \,{K_1}\left( {\!2\sqrt{\!\frac{x}{{{\psi _E}\rho \,{\Omega _1}{\Omega _2}}}} } \right) }}{{1 + x}}dx}. \end{aligned}$$
(36)

Proof

See Appendix 3. \(\square\)

3.3.3 Ergodic rate at \(D_{2}\) for user relaying with direct link

The ergodic rate at \(D_{2}\) is given by

$$\begin{aligned} {R_{{D_2},dir}} = E\left[ {\frac{1}{2}{{\log }_2}\left( {1 + \min \left( {{\gamma _{2,{D_1}}},\gamma _{{D_2}}^{MRC}} \right) } \right) } \right] . \end{aligned}$$
(37)

Theorem 6

From (37), the ergodic rate at \(D_{2}\) can be computed by (see(38))

$$\begin{aligned} R_{{D_2},dir}\!=\!\frac{1}{{2\ln 2}}\int \limits _0^{\frac{{{\alpha _2}}}{{{\alpha _1}}}} {\left[ {\frac{{{e^{\!-\!\frac{x}{{\psi _{I}\rho \left( {{\alpha _2} - {\alpha _1}x} \right) {\Omega _1}}}}}}}{{1\!+\!x}}} \right. } \left. {\!-\!\frac{{\int _0^\infty {\int _{\frac{x}{{\psi _{I}\rho \left( {{\alpha _2}\!-\!{\alpha _1}x} \right) }}}^\infty {\frac{1}{{{\Omega _1}{\Omega _0}}}\left( {1\!-\!{e^{\!-\!\frac{{x\left( {y{\alpha _1}\rho \!+\!1} \right) \!+\!y{\alpha _2}\rho }}{{z\rho \psi _{E}{\Omega _2}\left( {y{\alpha _1}\rho \!+\!1} \right) }}}}} \right) {e^{\!-\!\frac{y}{{{\Omega _0}}}\!-\!\frac{z}{{{\Omega _1}}}}}dydz} } }}{{1\!+\!x}}} \right] dx. \end{aligned}$$
(38)

Proof

See Appendix 4. \(\square\)

Remark 2

The ergodic rate in the asymptotic expression at \(D_{2}\) for high SNR region \(\rho \rightarrow \infty\) is given by

$$\begin{aligned} R_{{D_2},dir}^{\infty } = \frac{1}{{2\ln 2}}\int \limits _0^\infty {\frac{{1 - {F_X}\left( x \right) }}{{1 + x}}dx} \end{aligned}$$
(39)

From (39), this expression can be deployed by

$$\begin{aligned} R_{{D_2},dir}^{\infty } = \frac{1}{{2\ln 2}}\int \limits _0^{\frac{{{\alpha _2}}}{{{\alpha _1}}}} {\frac{{2\sqrt{\frac{x}{{{\psi _E}\rho \,{\Omega _1}{\Omega _2}}}} \,\!{K_1}\!\left( {2\sqrt{\frac{x}{{{\psi _E}\rho \,{\Omega _1}{\Omega _2}}}} } \right) }}{{1 + x}}dx} \end{aligned}$$
(40)

Proof

See Appendix 5. \(\square\)

3.3.4 Ergodic rate of the system for user relaying without direct link

The ergodic rate of system is determined by

$$\begin{aligned} \tau _{r,nodir} = R_{{D_1}} + R_{{D_2},nodir}, \end{aligned}$$
(41)

where \(R_{{D_1}}\) and \(R_{{D_2},nodir}\) can be obtained from (32) and (34), respectively.

3.3.5 Ergodic rate of the system for user relaying with direct link

The ergodic rate of system is thus expressed by

$$\begin{aligned} \tau _{r,dir} = R_{{D_1}} + R_{{D_2},dir}, \end{aligned}$$
(42)

where \(R_{{D_1}}\) and \(R_{{D_2},dir}\) can be obtained from (32) and (38), respectively.

3.4 Energy efficiency

The EE can be determined as the ratio of the total data rate over the total consumed power in entire network, which is given by \(\mathrm{{EE}} \buildrel \Delta \over = \frac{R}{{{P_S} + {P_r}}}\). The energy efficiency of user relaying systems can be given as

$$\begin{aligned} E{E_\phi } = \frac{{2\tau _\phi ^{HD}}}{{\rho \left( {1 + {\psi _E}{\Omega _1}} \right) }}, \end{aligned}$$
(43)

where \(\phi \in \left( {t,r} \right)\), denotes the system energy efficiency in DLT mode and DTT mode, respectively.

4 Results and discussion

4.1 Simulation parameters and scenarios

Table 2 Simulation Parameters
Full size table

In this section, Monte Carlo based simulation scenarios are performed in Matlab to verify the derived analytical results. The simulation parameters of the system model are listed in Table 2. In addition, we use the conventional OMA as a counterpart for comparison. The operation of this scheme is described as follows. During the first phase of time block, the information \(x_{1}\) is transmitted to \(D_{1}\) by S. During the second phase of time block, the information \(x_{2}\) is sent to \(D_{1}\) by S. Lastly, during the third phase of time block, \(D_{1}\) decodes and then forwards \(x_{2}\) to \(D_{2}\).

4.2 Outage probability versus SNR and \(\beta\)

Fig. 3
figure 3

Outage probability of two users versus transmitting SNR in cases of no direct link and direct link

Full size image

Figure 3 describes the relation between the outage probability and SNR of from −10 to 40 dB in case of \(\beta =0.7\). As shown in the figure, User 1 obtains a higher outage probability than User 2. In particular, with increasing SNR, the outage probability of both users decreases approximately linear. As a result, the gap width of these curves is bigger more and more. It means that the User 2 achieves a higher outage probability than User 1 in high SNR regime. Compared with OMA in high SNR regime, it is seen that the outage probability of User 1 for C-NOMA without direct link is lower. Besides, the outage probability of User 1 for OMA is also higher than that for C-NOMA in high SNR. Moreover, the User 2 for C-NOMA achieves a lower outage probability than that for OMA in both no direct and direct link cases. However, compared between direct link and no direct link, the C-NOMA scheme with direct link achieves a lower outage probability than C-NOMA scheme without direct link. The indicated curves for these cases correspond with the maker-red line and blue line in the figure. Obviously, the outage probability for C-NOMA with direct link is lowest as compared to both C-NOMA without direct link and OMA. It can be explained that the received information at User 2 in case of direct link existence between the BS and User 2 includes the one sent from BS and other one sent from the relay user 1. Thus, dropped package percentage at User 2 is lower as compared to the case of no direct link existence. In addition, we can base on the Eqs. (13), (14), (16), (18), (19), (23), (24), (25) to explain for these features. Therefore, it is shown that the C-NOMA scheme with direct link has a low outage probability over the C-NOMA without direct link as well as OMA.

Fig. 4
figure 4

Outage probability of two users versus \(\beta\) in case of no direct link and direct link

Full size image

Similarly, Fig. 4 shows the outage probability versus \(\beta\), where beta is from 0 to 1. It is observed that the outage probability of the User 2 for C-NOMA scheme with direct link is the lowest among the curves for C-NOMA without direct link and OMA for both users. For comparison of the outage probability of User 1 for both C-NOMA and OMA, we can see that the curve for C-NOMA is always below that for OMA and thus the probability of User 1 for the C-NOMA achieves better than that for OMA. Moreover, the outage probabilty between direct and no direct links is different in each user. This is shown in the maker red curve and the maker green curve in the figure corresponding with direct OMA and without direct OMA and that the outage probability for direct OMA is much lower than that for without direct OMA. Besides, the probability of User 2 for OMA with direct link is lower than that for C-NOMA without direct link. This means that the OMA scheme is better than the C-NOMA without direct link. However, the outage probability of User 2 for C-NOMA with direct link is lower than that for OMA with direct link. Therefore, we can conclude that the C-NOMA with direct link outperforms the C-NOMA without direct link as well as OMA. These can be explained similarly to Fig. 3 as well as based on Eqs. (12), (13), (16), (18), (19), (23), (24), (25). In addition, it can be seen that when the \(\beta\) is in range of from 0.1 to 0.65, the outage probability of User 2 for C-NOMA with direct link is considerably lower as compared to others. In range of from 0.65 to approximately 0.9 and from 0 to 0.1, this probability decreases and increases gradually, respectively. As a result, the gap width between the curve of the outage probability of User 2 for C-NOMA with direct link and the others achieves the biggest in range of 0.1 to 0.65. It means that we can choose \(\beta\) in this range to obtain a better outage probability for the system model.

4.3 Throughput and ergodic versus SNR and \(\beta\)

Fig. 5
figure 5

The throughput of two users versus \(\beta\) in cases of no direct link and direct link

Full size image

Figure 5 decribes the throughput versus \(\beta\) in from 0 to 1. From the figure, it is shown that the throughput of User 1 for C-NOMA is considerably higher than that for OMA. However, this throughput trends to decrease quickly when the \(\beta\) towards to 1. This is because that as the power splitting ratio \(\beta\) increases, the power allocated to User 1 is lower, thus resulting in a decreased throughput of User 1. Furthermore, the throughput of User 2 for C-NOMA with direct link is the highest among the graphs illustrating for User 2 in cases of C-NOMA and OMA. We can see that the maker blue line of User 2 for C-NOMA with direct link is higher and approximately constant as compared that for C-NOMA without direct link as well as OMA, i.e. the maker green line and the maker magenta line, respectively. Besides, the throughput of User 2 for these three cases is almost constant in range of \(\beta\) from about 0.1 to 0.8. This means that we can choose a suitable value of \(\beta\) to satify the tradeoff between the throughput of User 1 and the throughput of User 2 for the system model. Additionally, the figure also shows that the throughput of User 2 for C-NOMA is lower than that for C-NOMA without direct link. Thus, the C-NOMA scheme with direct link is superior to the C-NOMA without direct link and C-NOMA.

Fig. 6
figure 6

The ergodic rate of two users versus \(\beta\) in cases of no direct link and direct link

Full size image

Figure 6 plots the ergodic rate as a function of \(\beta\) in from 0 to 1. The figure shows that the ergodic rate of User 1 for C-NOMA is considerably higher than that for OMA. However, these curves degrade quickly when the \(\beta\) towards to 1. The reason is similar to Fig. 4. It can be also explained according to Eqs. (32), (34), (36), (38). Besides, the ergodic rate of User 2 for C-NOMA with direct link is the highest as compared to that of User 2 in cases of C-NOMA and OMA. Specifically, the ergodic rate of User 2 for C-NOMA with direct link is about four times higher than that for OMA. Futhermore, the ergodic rate of User 2 is almost constant in range of \(\beta\) from about 0.1 to 0.9. Therefore, one can choose a suitable value of \(\beta\) to satify the tradeoff between the ergodic rate of User 1 and the ergodic rate of User 2 for the system model. From Eqs. (32), (34), (36), (38), the ergodic rate of User 2 depends on the \(\beta\) less than that of User 1. Thus, the C-NOMA scheme with direct link outperforms the C-NOMA without direct link and OMA.

4.4 Energy efficiency

Fig. 7
figure 7

Energy efficiency of two users for the PSR protocol in cases of without direct link and direct link

Full size image

Figure 7 illustrates the energy efficiency according to SNR from -10 to 40 dB. It is shown that the EE for C-NOMA with direct link achieves much higher than that for C-NOMA without direct link and OMA. In particular, with the SNR range of from -10 to 5 dB, this energy efficiency is large but linearly decreases as the SNR value increases. When SNR range is from 5 to 40 dB, the energy efficiency for both C-NOMA with and without direct link and OMA asymptotically decreases to 0. Therefore, it can be concluded that the C-NOMA scheme with direct link provides a better EE as compared among the schemes in low SNR regime.

Therefore, the simulation results are in accordant with theoretical calculations.

5 Conclusion

In this paper, a proposed EH scheme for SWIPT C-NOMA has been presented. The closed-form expressions of the performance were derived. The analytical results shown that the C-NOMA with direct link obtained a better outage probability over the OMA as well as C-NOMA without direct link. Numerical results provided that C-NOMA with direct link outperformed throughput and ergodic rate than OMA. Besides, the C-NOMA with direct link obtained a higher EE performance than the C-NOMA without direct link and OMA in low SNR region. The proposed system model can be applied for C-NOMA based wireless sensor networks where relaying sensor nodes can harvest RF energy from BSs to maintain their operation and assist to forward information to other sensor nodes. Futhermore, we can develope the system using multiple antennas or combine relay selection with multiple antennas to enhance the performance of the system.