Abstract
Background
Brazilian malaria control programmes successfully reduced the incidence and mortality rates from 2005 to 2016. Since 2017, increased malaria has been reported across the Amazon. Few field studies focus on the primary malaria vector in high to moderate endemic areas, Nyssorhynchus darlingi, as the key entomological component of malaria risk, and on the metrics of Plasmodium vivax propagation in Amazonian rural communities.
Methods
Human landing catch collections were carried out in 36 houses of 26 communities in five municipalities in the Brazilian states of Acre, Amazonas and Rondônia states, with API (> 30). In addition, data on the number of locally acquired symptomatic infections were employed in mathematical modelling analyses carried out to determine Ny. darlingi vector competence and vectorial capacity to P. vivax; and to calculate the basic reproduction number for P. vivax.
Results
Entomological indices and malaria metrics ranged among localities: prevalence of P. vivax infection in Ny. darlingi, from 0.243% in Mâncio Lima, Acre to 3.96% in Machadinho D’Oeste, Rondônia; daily human-biting rate per person from 23 ± 1.18 in Cruzeiro do Sul, Acre, to 66 ± 2.41 in Lábrea, Amazonas; vector competence from 0.00456 in São Gabriel da Cachoeira, Amazonas to 0.04764 in Mâncio Lima, Acre; vectorial capacity from 0.0836 in Mâncio Lima, to 1.5 in Machadinho D’Oeste. The estimated R0 for P. vivax (PvR0) was 3.3 in Mâncio Lima, 7.0 in Lábrea, 16.8 in Cruzeiro do Sul, 55.5 in São Gabriel da Cachoeira, and 58.7 in Machadinho D’Oeste. Correlation between P. vivax prevalence in Ny. darlingi and vector competence was non-linear whereas association between prevalence of P. vivax in mosquitoes, vectorial capacity and R0 was linear and positive.
Conclusions
In spite of low vector competence of Ny. darlingi to P. vivax, parasite propagation in the human population is enhanced by the high human-biting rate, and relatively high vectorial capacity. The high PvR0 values suggest hyperendemicity in Machadinho D’Oeste and São Gabriel da Cachoeira at levels similar to those found for P. falciparum in sub-Saharan Africa regions. Mass screening for parasite reservoirs, effective anti-malarial drugs and vector control interventions will be necessary to shrinking transmission in Amazonian rural communities, Brazil.
Similar content being viewed by others
Background
Both the morbidity and mortality associated with malaria have substantially decreased worldwide and in several endemic countries in Africa, South-East Asia and South America, including Brazil [1, 2]. However, in South-East Asian and South American countries, malaria control programmes face a challenging situation because of the high proportion of Plasmodium vivax malaria, lack of sustainable funding, and emerging resistance to anti-malarial drugs and available insecticides [1]. In Venezuela, South America, malaria increased by 365% from 2000 to 2015, with an additional 68% increase in 2017 [3]. In Brazil, malaria incidence increased by 47% in 2017 compared with 2015, including Plasmodium falciparum that emerged in areas previously free of this pathogen. The intensity of malaria transmission in Brazil is highly heterogeneous, with regions of high risk interspersed with others of moderate, low or no risk [4]. Furthermore, locations with the heaviest burden of malaria are those in the poorest and most remote regions of the Amazon River basin, in the states of Amazonas, Acre, Amapá, Pará and Roraima, with the occurrence of both P. falciparum and P. vivax (https://public.tableau.com/profile/mal.ria.brasil#!/), and the presence of subpatent or submicroscopic infection [5, 6]. Understanding spatiotemporal heterogeneities in the intensity and risk of transmission is important for planning and delineating measures and strategies to be adopted by an effective malaria control programme, as well as when disease incidence is decreasing, and elimination is forthcoming [7].
The dynamics of human Plasmodium transmission are shaped by complex interconnections of determinants, including those of vector biology, blood-feeding behaviour of vector species, temperature, precipitation, environment, ecology and human behaviour that determine the degree of human exposure to infectious mosquito bites [7,8,9,10]. Microclimatic changes caused by deforestation and forest degradation are associated with environmental and ecological changes that can increase the abundance of the primary mosquito vector Ny. darlingi, thereby increasing the malaria burden across Amazonian landscapes [11,12,13]. Comprehending the effects of environmental change on the malaria transmission cycle requires further knowledge of the locally relevant determinants, including entomological factors, such as the accurate identification of mosquito species competent for Plasmodium infection and directly involved in transmission [7]. The many components of malaria transmission include those of vector competence, vectorial capacity and transmission potential [14].
Mathematical models play an important role in investigating the mechanisms and processes that determine the transmission of malaria, and thus for malaria control and elimination. The mathematical models proposed by Ronald Ross and George Macdonald [8, 15] describe quantitatively the mechanisms involved in the dynamics of Plasmodium dispersion in a population composed of infected and susceptible hosts [9, 16]. The Ross–Macdonald model assumes homogeneous and random transmission of pathogens in a host population of indeterminate size [9]. The variables of the model include the population density of the mosquito vector in relation to humans, daily female survival, time required to complete a blood feeding cycle with subsequent oviposition, anthropophilism, and the extrinsic incubation period of the pathogen in the mosquito population. These parameters comprise the vectorial capacity that is the entomological variant of the basic reproductive rate for malaria (R0) [17]. Interventions for controlling malaria, such as the reduction of mosquito populations and human exposure to infectious bites, have been based largely on the components of the vectorial capacity formula of locally relevant mosquito species [16]. In addition to vectorial capacity, the basic reproduction number (R0) metric indicates the potential of an introduced Plasmodium species to propagate in a human community, given the local epidemiological data of malaria and ecological factors of the transmission cycle [7].
The Plan for Elimination of Malaria in Brazil proposed in 2015 by the Brazilian Ministry of Health includes the decline of both P. vivax and P. falciparum malaria across the Amazon River basin. However, in 2016–2017, Brazil was challenged by malaria resurgence, including P. falciparum malaria in areas where the pathogen had been eliminated. Plasmodium vivax malaria currently comprises more than 80% of the total malaria cases reported in Brazil [18]. A highly significant positive correlation between number of impacted forest patches less than 5 km2 and malaria cases were recently found, and that these patch sizes accounted for greater than ~ 95% of all patches in numerous study areas across the Brazilian Amazon for multiple years [13].
Nyssorhynchus darlingi is the primary malaria vector in several regions of the Brazilian Amazon River basin, and more broadly in the Amazon biome in South America. Despite its public health importance, field investigations focusing on the entomological components of malaria risk are few in number and restricted to a small portion of the massive geographical area of the Amazon. Moreover, vector competence and vectorial capacity of Ny. darlingi estimated employing contemporary entomological field data and locally acquired plasmodial infection in areas across the Brazilian Amazon are either very limited or nonexistent. Consequently, the need for sound and comprehensive field studies to empirically measure and evaluate the dimension and transmission potential of the most prevalent malaria in the Brazilian Amazon is necessary. The objectives of the study were to: (1) determine the vector competence and vectorial capacity of Ny. darlingi to P. vivax malaria; and (2) calculate the basic reproduction number (R0) for P. vivax (PvR0) malaria in five municipalities of the Brazilian Amazon. The primary focus of the analysis was Ny. darlingi because it was the most frequently found species in all localities, and P. vivax malaria because it comprised the great majority of cases during the period of field collections.
Methods
Study sites and mosquito adult collection
Females of the subfamily Anophelinae were collected in 36 houses of 26 communities in five municipalities in the Brazilian Amazon states of Acre, Amazonas and Rondônia states (Fig. 1; Table 1). The study locations were in rural settlements in areas with moderate to high endemicity of P. vivax malaria (Table 1; Additional file 1), where most infections were locally-acquired. To guide the choices of field collection communities, the mean annual malaria parasite incidence (annual parasite incidence, API ≥ 30) of local P. vivax infections in the previous several months and during the period of field collections in 2015 (http://portalms.saude.gov.br/saude-de-a-z/malaria/situacao-epidemiologica-dados), and 2017 (public data are available at https://public.tableau.com/profile/mal.ria.brasil#!/), as well as local information, were used as a proxy of the incidence. In addition, the selection of field localities was based on the level of forest cover, land use, and density of forest border as proxies of the presence of human and domestic animals. Coincidentally, the chosen areas were subject to discontinuous or negligible malaria control interventions, except for those measures focusing on either rapid or optical microscope diagnosis of Plasmodium infection in symptomatic humans, followed by immediate drug treatment. The use of insecticide-impregnated bed nets was either discontinuous or haphazardly employed in the communities.
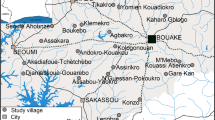
Specimen collection sites in five municipalities in the states of Acre, Amazonas and Rondônia, Brazil. Human landing catch (HLC) houses are represented by black dots. The numbers represent the municipalities as following: 1 Mâncio Lima; 2, 6A, 6B Cruzeiro do Sul; 3 São Gabriel da Cachoeira; 4 Lábrea; 5 Machadinho D’Oeste
The municipalities of Cruzeiro do Sul and Mâncio Lima are in the region of the Juruá River basin, western Acre state; Machadinho D’Oeste is situated in the Machadinho River basin, along highway BR-364, and Lábrea municipality is alongside the Boa Água River, a tributary of the Purus River, west of the BR-230 Brazilian Trans-Amazonian highway. The most northern municipality, São Gabriel da Cachoeira, is in northwestern Brazil at the frontier of Colombia and Venezuela, in the Upper Negro River region (Fig. 1).
The municipalities of Cruzeiro do Sul, Mâncio Lima and Lábrea have a tropical climate with significant rainfall most of the year, and a short dry season. The climate is classified as Am according to Köppen and Geiger with average temperature varying from 26.4 °C in Lábrea to 25.3 °C in Cruzeiro do Sul, and average annual rainfall values of 2139 mm (Cruzeiro do Sul) to 2318 mm (Lábrea). Machadinho D’Oeste has a tropical climate, with less rainfall in the winter than in the summer. According to Köppen and Geiger, the climate classification is Aw, with an average temperature of 25.3 °C, and average annual rainfall of 2117 mm. The climate of São Gabriel da Cachoeira region is tropical with significant rainfall throughout the year, even during the driest month. According to Köppen and Geiger, this climate classification is Af, with the average annual temperature of 26.4 °C, and the average annual rainfall of 2909 mm (https://pt.climate-data.org/america-do-sul/brasil/).
Female adult collections were conducted from April to November, during the wet–dry transition, and in the dry season (Table 1). Collections were outdoors in the peridomestic environment within ~ 5 m of each of 36 houses. Considering the 26 rural communities separately, houses chosen for human landing catch (HLC) were at least 2.5 km apart and were positioned in the centre of a 1 km radius circle to avoid sampling more than one house within the same 3.14 km2 area. Each black dot in Fig. 1 represents a house that was selected for conducting the HLC mosquito collections. Although there was active malaria transmission and reported cases in all communities (Table 1), house selection within rural communities was not based on malaria cases among the residents in the collection period of time. Furthermore, selection was also guided by the level of forest cover, land use, and density of forest border (Fig. 1).
Human landing catch collections were carried out one night each 36 houses, from 18 h:00 until 0 h:00 (Table 1). Following the field protocol, it was possible to collect in more than one house in some locations, for example, in PA Umari, Boa Água (Sivep location 163), two houses were sampled, each collection was carried out one night from 18 h:00 until 0 h:00. One or two collectors worked each night. Variation in the number of collectors was due to their availability during the field trip. The mosquito sampling effort was 216 h-collection, distributed as follows: Lábrea, Machadinho D’Oeste and Mâncio Lima 36 h each, São Gabriel da Cachoeira 42 h, and Cruzeiro do Sul 66 h. Every hour, female mosquitoes were euthanized with ethyl acetate (C4H8O2) vapors in the field and stored in silica gel separated by date, location, house and hour of collection. Specimens were morphologically identified to species level by MAMS, labeled and stored individually with silica gel at room temperature for subsequent analysis.
Mosquito processing
Genomic DNA was extracted from whole, adult female Ny. darlingi using Qiagen DNeasy Blood & Tissue Kit (Hilden, Germany). All Ny. darlingi DNA samples were tested for Plasmodium spp. infection following [19], with DNA pools of up to five individuals containing equal amounts of gDNA. Mosquito samples with DNA concentrations of < 1.0 ng/µL or > 15 ng/µL were tested individually and not pooled. In instances where the species of Plasmodium could not be detected with the triplex assay, PCR amplification and agarose gel (2%) electrophoresis of PCR products was performed using primer pairs for P. vivax and P. falciparum [20]. Each PCR reaction contained 1× PerfeCTa qPCR ToughMix, Uracil N-glycosylase (UNG), ROX (Quanta Biosciences, USA), 0.3 μM of each primer, ultrapure water, and 2 μL genomic DNA, with a total volume of 20 µL. Cycling conditions were as follows: 5 min UNG-activation hold at 45 °C and a denaturation step for 10 min at 95 °C, followed by 50 cycles of 95 °C denaturation for 15 s and 60 °C annealing/elongation for 1 min.
Malaria epidemiological data
Data on the number of cases of malaria by epidemiological week and annual parasite incidence (IPA) of P. vivax (Table 1; Additional file 1) were requested by first author from the Ministry of Health, Sistemas de Informações de Vigilância Epidemiológica (SIVEP) Malaria [18], through the Electronic System of the Citizen Information Service (Sistema Eletrônico do Serviço de Informações ao Cidadão - e-SIC) (https://esic.cgu.gov.br/sistema/site/index.aspx), protocols # 25820001316201742, # 25820003892201813, # 25820004426201847, and # 25820004717201835. Because asymptomatic infections are not included in the SIVEP Malaria [18] platform, only locally acquired symptomatic infections were employed in the mathematical modelling analysis.
Human-biting rate, prevalence of infection in mosquito, estimation of vector competence, vectorial capacity and basic reproduction number
Vector competence is defined as “the ability of a vector to transmit a disease” [21]. It normally comprises the capacity of a vector to be infected, maintain and transmit an infectious agent. In the present study, vector competence was defined as the probability that an infected mosquito generates a new infection when it bites a susceptible human [14]. Vector competence was initially defined by [22] in pioneering work on malaria modelling. Vector competence is denoted b throughout the current paper.
The analysis began by considering malaria incidence in the studied rural communities (Table 1). The data were obtained from SIVEP Malaria [18] through the Citizen Information Service, Ministry of Health of Brazil (https://esic.cgu.gov.br/sistema/site/index.aspx). The incidence of malaria was calculated in rural communities at the time of mosquito collection, denoted Incidence(t), that is the number of new malaria cases per unit time. It is equal to the product of the force of infection, λ (incidence-density rate or per capita incidence), times the number of susceptible humans, SH(t). It is also the product of the ratio of mosquitoes-to-humans, NM(t)/NH(t), times the mosquito biting rate, a, times the vector competence, b (see below), times the prevalence of Plasmodium infection in the mosquitoes, \(I_{M} (t)/N_{M} (t)\), times the number of susceptible humans, \(S_{H} (t)\), or:
Incidence data from the five municipalities studied were then fitted to the continuous function:
Fitting of the incidence data was restricted to the period of data collection, which occurred in the same season for all localities. Therefore, only the growing phase of the annual malaria seasonal cycle was considered for this model. The exponential form chosen was restricted to the period of the study. Figures 2, 3, 4, 5 and 6 show the fitting of Eq. (2) to the actual data on malaria incidence in each of the five collection localities.
As mentioned above, vector competence, b, is the probability that a new human infection is produced when a fraction of infected mosquitoes bite humans with rate a. It can be calculated from the incidence of malaria, using the equation:
where t is the moment of data collection. Therefore, given at day t: the malaria incidence at the site and the malaria prevalence in the mosquitoes, calculating the human-biting rate (HBR) from the HLCs (see below) and the number of susceptible humans from the history of malaria, the vector competence at day t from Eq. (3) can be calculated.
As mentioned above, the HBR is the number of bites that a mosquito population inflicts on humans per unit time [23]. In this study, the HBR was obtained by the number of mosquitoes collected on HLC per night per catcher. It is the product of the ratio of mosquitoes-to-humans, \(N_{M} (t)/N_{H} N_{M} (t)/N_{H}\), times the mosquito daily biting rate, a:
HBRt values for the five municipalities studied were obtained from the number of mosquitoes captured by HLC per collector, per night, at day t. It is assumed that captured mosquitoes approached the collector to bite. Therefore, the number of mosquitoes collected in each HLC corresponds to the HBRt of these specific mosquitoes in these specific collection sites.
To estimate the probability of acquiring malaria at day t, that is, on the day of the field collections, the weekly incidence data, available from SIVEP Malaria [18], were disaggregated. For this the following procedures were applied. Firstly, it was calculated the number of malaria cases in the time interval between t0 and t1, which is simply the integral of the incidence in this interval, calculated by the equation:
The daily number of malaria cases between week t0 and week t1+1/7, Ht, therefore, is the difference between the number of malaria cases in the time interval between t0 and t1+1/7 minus the number of malaria cases in the time interval between t0 and t1. It is calculated by the equation:
In the calculation of the daily incidence, it was assumed a stable situation, and estimated the remaining susceptible population, SH, from the annual parasite incidence (API), and subtracted the number of parasite positive individuals from the total population of each of the studied locations.
The vectorial capacity at day t (VCt) [24] is the daily number of potential infections produced by a single infective individual, IH. It is calculated from the per capita daily incidence, \(h_{t} = \frac{{H_{t} }}{{S_{Ht} }}\), by the equation [25, 26]:
where τ is the total incubation period (both extrinsic inside the mosquito and intrinsic inside the human hosts) and was assumed to be equal to 1 week, and bt is now:
The first part of Eq. (7) is the same as the one originally presented in [25] with different notation. It can be interpreted as follows. Assuming a Poisson distribution, the probability of receiving no potentially infective inoculation is \(\exp \left( { - V_{C} I_{H} (t - \tau )t} \right)\), and the probability of receiving at least one potentially infective inoculation is \(1 - \exp \left( { - V_{C} I_{H} (t - \tau )t} \right)\), a fraction bt of which is actually infective. Note that h is interpreted in Eq. (7) as the probability of one malaria case produced by one single infective human individual IH who acquired the infection t − τ days ago. Note that the “difference” t − τ is not computed in the calculations.
The basic reproduction number, R0, is the number of infections produced by a single infective individual, IH, in an entirely susceptible population throughout his/her infectiousness period, 1/γ [27]. It is calculated from the vectorial capacity by the equation:
where c is the probability that an infected individual when bitten by a susceptible mosquito generates a new infection in the mosquito [22]. Although the value of R0 varies throughout the seasons of the year, this value was calculated for the day of data collection.
Results
The human population in each municipality, and results of the variables from the field-collected data employed in the mathematical modelling, namely, the P. vivax annual parasite incidence (API), the remaining susceptible human population (SH), the prevalence of P. vivax infection in Ny. darlingi mosquitoes, \(I_{Mt} /N_{Mt}\), and the daily human-biting rate per human collector, \(HBR_{t}\), are shown in Table 2 and Additional file 2.
Results of the analyses in Table 2 demonstrated that all five studied locations present high levels of P. vivax malaria endemicity. This is reflected mainly in the high API values that range from 144 in Machadinho D’Oeste to 279 in Lábrea, and the high prevalence of Ny. darlingi to P. vivax infection. In Lábrea, the estimated HBR was very high, reaching 66 bites per human per 6-h per night, with 0.246% of Ny. darlingi found RT-PCR positive for P. vivax, and the API value was 279 per 1000 population. The highest values of prevalence of P. vivax infection in Ny. darlingi were found in Machadinho D’Oeste (3.96%), São Gabriel da Cachoeira (2.9%) and Cruzeiro do Sul (1.5%). The estimated HBRs were 23 in Cruzeiro do Sul, 39 in Machadinho D’Oeste, 52 in São Gabriel da Cachoeira and 66 in Lábrea. The API ranged from 144 in Machadinho D’Oeste, 150 in São Gabriel da Cachoeira and 279 in Lábrea. The second highest API value (API = 241) was estimated for Mâncio Lima, and the prevalence of P. vivax infection in Ny. darlingi was 0.243%, a value slight lower than that found in Cruzeiro do Sul.
Results of mathematical modelling analysis to estimate entomological parameters of malaria, namely, the daily malaria incidence, ht; vector competence, bt; vectorial capacity, \(V_{Ct}\); and the basic reproduction number, R0 are shown in Table 3.
The vector competence (bt) values ranged tenfold from the lowest in São Gabriel da Cachoeira (0.00456) to the highest in Mâncio Lima (0.0476). These differences were inversely correlated with the malaria intensity metrics, the vectorial capacity (VCt) and the basic reproduction number (R0). The VCt calculated for HLC Ny. darlingi in São Gabriel da Cachoeira was 1.4 (1.3–1.5), whereas in Mâncio Lima it was 0.0836 (0.0809–0.0862). This variation was likely due to the indirect way vector competence was estimated. For the observed high malaria incidence and prevalence of infection in the vector, very low vector competence suffices to explain the data. The two highest estimated malaria incidences at day t values were found in Machadinho D’Oeste (174) and São Gabriel da Cachoeira (142), and the lowest value in Mâncio Lima (45). The highest probability of having malaria at day t was found in Machadinho D’Oeste (0.0104), whereas the lowest was in Cruzeiro do Sul (0.00167).
Figure 7 shows the correlation between the prevalence of P. vivax in the mosquitoes and both the vectorial capacity and the basic reproduction number (R0). The association is clearly linear, and the trend is positive. The difference between the vectorial capacity and the basic reproduction number is only by scale since the latter is the result of the multiplication of the former by a constant \(\frac{c}{\gamma }\). The association between both the vectorial capacity and the basic reproduction number and the prevalence of P. vivax in the mosquitoes is highly non-linear. This non-linearity can be understood if Eq. (8) substitutes into Eq. (7) to obtain:
Discussion
Strategic planning for malaria control and prevention are usually tailored based on categorization of API, without knowledge of the determinants of malaria risk that impact the propagation of Plasmodium parasite and intensify transmission in a region [7]. Thus, the success in reducing the disease incidence is continuously threatened by a combination of multiple determinants that can increase intensity of malaria transmission. For example, anthropogenic changes in the forest environment that increase the local mosquito vector potential [12, 13], in addition to human-related determinants [7]. Among a multitude of factors, intensive human movement can support the introduction of new infections acquired in other areas with active transmission. In addition, poor local housing conditions, economic failures, insufficient financial investment in malaria control and poorly managed surveillance programmes can favour the reemergence of malaria and intensify transmission to higher levels [7, 10].
The choice of rural settlements to conduct mosquito collections was not random. Localities and municipalities with active malaria transmission and reported cases in the previous and/or in the month of field collections were selected (Table 1). This approach somewhat biased the data because it tends to overestimate the number of infected mosquitoes, especially in areas where transmission is expected to be heterogeneous. To minimize the bias, the selection of houses for HLC collections was also guided by the level of forest cover, land use, and density of the forest border (Fig. 1). In addition, houses were at least 2.5 km apart to avoid sampling in houses situated within a circle of 1-km radius. What is more, considering that this is a methodological study conducted to estimate the malaria metrics in rural communities with moderate to high transmission intensity, the choice for field-collections does not invalidate the results of the analyses. Furthermore, this is the first study to calculate the vectorial capacity of vectors based on empirical data of malaria incidence in Brazil.
In the analyses, it was used empirical data from mosquito field-collections and reported data on local malaria incidence to calculate, through simple mathematical techniques, three key parameters related to malaria transmission intensity: vector competence, vectorial capacity and basic reproduction number (R0). The mathematical approach adopted in this study consists of equations relating the reported malaria incidence to vector competence and vectorial capacity. From the latter, it was calculated PvR0 in the Amazonian rural communities. Likely, the mathematical approach has limitations, for instance, it is assumed that all individuals in a certain population are identical and equally exposed to Plasmodium infection. It is known that human-to-mosquito transmission efficiency may change as malaria prevalence changes, however it was assumed a fixed value for all localities, obtained from the published literature. This is due to the lack of studies addressing this important parameter. As the major objective is to propose a new method for calculating the malaria metrics, this limitation does not invalidate the approach adopted in the study. However, further studies on this topic will be necessary to improve the methodological approach proposed. Another limitation is subpatent or submicroscopic infections that were not considered in the analysis because of lack of information for the localities studied. Inclusion of asymptomatic infections in the analyses could impact the scale, but the method would be the same.
The proportion of Ny. darlingi in HLC collections in the peridomestic environment was similar to values obtained in previous studies carried out in other areas across the Brazilian Amazon [30,31,32,33]. Similarities among results of diverse studies may be caused by the high degree of anthropophily of Ny. darlingi. This mosquito vector is specially attracted to human-specific volatiles, hence the effectiveness of HLC compared with CDC-LT and the mosquito magnet trap, among other trap types [34,35,36,37]. In the current study, the number of Ny. darlingi mosquitoes on HLC collectors ranged from 23 to 66 specimens per collector per 6 h night (Table 1). These findings are of the same order of magnitude as those by Tadei and collaborators [30] in the Brazilian Amazon. However, the range is narrower compared with a recent study from Amazonian Peru, where using HLC in the peridomestic environment, the number of Ny. darlingi in the dry season versus the rainy season per collector per 12 h night ranged from 1.5 to 250.5 specimens (average of two nights) [38]. In the heterogeneous Amazonian landscapes, spatial distribution and prevalence of Ny. darlingi depends on the level of precipitation, temperature, presence of standing water, level and pattern of forest fragmentation, size and abundance of deforested patches, proximity of larval habitats to human houses, and reallocation of water associated with land-use [39,40,41,42,43]. Thus, the range from 23 to 66 mosquitoes per catcher per 6 h night is likely due to a combination of environmental and ecological factors that influence the seasonal distribution of the species. In addition, distinct from Iquitos, field collections in the localities studied were carried out in the wet-dry and dry seasons, when malaria transmission intensifies in the Brazilian Amazon.
The results of the mathematical modelling conducted to estimate the prevalence of P. vivax in Ny. darlingi are similar to the levels of variation found in previous studies. Typically, Ny. darlingi vector infection rate has been recorded in the published literature as ~ 1–2% [37, 44, 45]. In contrast, in some high-malaria risk areas in the Brazilian Amazon, the prevalence rate of Plasmodium in Ny. darlingi was unexpectedly low (less than 0.5%) [30, 46]. This could be explained by the relatively low number of specimens examined (n = 308), even though it was during the peak malaria transmission season (July–August). Local variation in the prevalence rate was also detected in districts of the municipality of Boa Vista, Roraima. Whereas Silva Vasconcelos et al. [47] found an 8.5% Plasmodium prevalence rate in Ny. darlingi from two riverine districts, Póvoa et al. [48] showed that the overall Plasmodium infection rate was 2.1% in six distinct districts in the same municipality. The highest prevalence of P. vivax infection in Ny. darlingi (approximately 4%) was found in Galo Velho settlement (Table 2) in Machadinho D’Oeste, Rondônia. This value is closer to the infection rate found in Anopheles funestus in Tanzania (6.3% according to Taylor [49]) than to that of a Neotropical malaria vector. The second highest prevalence of P. vivax infection in the main vector (approximately 2.9%) was detected in São Gabriel da Cachoeira, Amazonas. Although the infection rate was lower than in Machadinho D’Oeste, the HBR was ~ 52 in São Gabriel da Cachoeira, whereas in Machadinho D’Oeste it was ~ 39. Considering the entomological potential for malaria transmission, mathematically quantified by the vectorial capacity (Table 3), one can assume that the effectiveness of Ny. darlingi in propagating P. vivax throughout in local population is similar. Interventions for reducing the number of mosquito infectious bites per human per day, and the overall number of mosquito bites, should be prioritized by malaria control programmes. Malaria commodities for vector control such as insecticide impregnated nets, indoor insecticide spraying, management of larval habitats, environmental modifications and household improvements can be appropriate for reducing human exposure to vectors. However, effectiveness of the vector control measures will depend on knowledge of mosquito vector biology and the environment that sustain the population [7].
Vector competence is defined in this study as the probability of one infected Ny. darlingi mosquito generating a human case of P. vivax malaria when biting a non-infected person. Results of the analyses showed relatively low values (from 0.46 to 4.8%). The tenfold variation observed is more likely due to local environmental characteristics rather than biological variation in P. vivax and Ny. darlingi from the various collecting locations. However, the potential for biological variation between sub-populations of Ny. darlingi with distinctive competencies for P. vivax cannot be excluded. By fitting their models to field data on malaria prevalence, Dietz et al. [25, 26] estimated that vector competence (g in their notation) resulted in 9.7% (± 1.7%) for Anopheles gambiae and An. funestus in Nigeria. This high level of vector competence is linked to both the exclusive focus on indoor vector collections and the long evolutionary history between P. falciparum and each of An. gambiae and An. funestus. Considering that the present study focused only on outdoor peridomestic collections of Ny. darlingi and on P. vivax, the observed range is unremarkable.
The negative correlation between mosquito infection rates and vector competence deserves a more detailed explanation. Note that, from Eq. (3), vector competence is the product of the per capita incidence rate (Incidence/SH) times the inverse of the HBR (NH/(aNM)) times the inverse of P. vivax prevalence in the mosquitoes (NM/IM). Therefore, for a given incidence level, for high values of HBR and high levels of P. vivax prevalence in the mosquitoes, the vector competence that would explain the observed variables would necessarily have low values. Conversely, for low values of HBR and low levels of P. vivax prevalence in the mosquitoes, vector competence that would explain the observed variables would necessarily have high values.
Vectorial capacity was calculated using Eq. (7) with inputs of the daily probability of one malaria case (estimated from incidence data using Eq. (5)) and the vector competence (from Eq. (3), above). The results are again of the same order of magnitude as those found by Dietz et al. [25, 26] for P. falciparum malaria in Nigeria. The maximum value these authors found was 21.74 in the village of Sugungum. However, they used a different formula for calculating vectorial capacity, the original Garret-Jones equation [24], which does not consider vector competence. That is, they computed vectorial capacity as the product of HBR by the factor apn(− ln p), where a is the daily mosquito biting rate, p is the daily probability of mosquito survival and n is the mosquito mortality rate. When vector competence was included in the factor apn(− ln p) (see [14] for a detailed discussion), the values obtained were very similar to the ones calculated. Therefore, the vectorial capacity values estimated for Ny. darlingi in transmitting P. vivax malaria are very high indeed.
Results of the estimation of the basic reproduction number (R0) showed values ranging from 3.3 to 58.7, obtained using Eq. (8), that is, the product of the vectorial capacity times a scaling factor comprised of the ratio between vector susceptibility and the infection and the recovery rate of humans from parasitemia, reflecting the variation in the vectorial capacity (Fig. 7). The maximum value of 58.7 means that one single human infected with P. vivax, in that specific location and time of data collection, was able to produce, throughout the mosquito population, almost 60 secondary malaria cases. This is an extremely high value, in the range of the estimations of R0 for malaria in Africa. More importantly, according to the reclassification of malaria endemicity proposed by Hay et al. [50], P. vivax endemicity was intense, stable and hyperendemic in Galo Velho settlement, Machadinho D’Oeste, and São Gabriel da Cachoeira. These values show the urgent need for implementing a combination of interventions for malaria control, that include insecticide-treated bed nets, indoor residual spraying when possible, and intensive treatment with anti-malarial drugs.
Both malaria transmission and its intensity are spatially and temporally heterogeneous in the Brazilian Amazon, including in the five municipalities in the present study. The biological, ecological and social processes that determine the effective dispersion of P. vivax propagation in a human community involve humans as hosts and a single vector species, Ny. darlingi. There are secondary vector species, but their presence in the outdoor and indoor human environments depends mostly on land use, presence of domestic vertebrates, and deforestation level [51, 52]. In the field collections carried out for this study, Ny. darlingi was the most abundant and the predominant species in the peridomestic area. Despite the constant presence of this species, the estimated vector competence, vectorial capacity and R0 showed variation among populations studied. The propagation and persistence of Plasmodium depends on the presence of hotspots for the pathogen and the capacity of the mosquito vector to disperse infectious bites in a human population with a distinct risk of being infected [9].
The estimated vector competence of Ny. darlingi to transmit P. vivax was low in the Brazilian Amazon region of Cruzeiro do Sul, Mâncio Lima, Lábrea, Machadinho D’Oeste and São Gabriel da Cachoeira. However, low vector competence appears to be offset by high biting rates and relatively high susceptibility to Plasmodium infection, as was demonstrated in experimental studies by Klein et al. [53] and other investigations reviewed by Hiwat and Bretas [32]. Moreover, female vector avoidance of defensive host behaviour by frequent feeding on lower legs and feet [34] might enhance the prevalence of Plasmodium infection in the vector and human populations. Plasticity in biting behaviour was observed in Ny. darlingi populations that shifted from biting mainly outdoors to more indoors in riverine communities near Iquitos, Peru, when the long-lasting insecticidal nets aged [38]. Such behaviour could increase the odds of Ny. darlingi exposure to an infectious human reservoir. Finally, low vector competence of Ny. darlingi for P. vivax infection may also be offset by increased survival in cases where preferred hosts are unavailable, and blood-feeding occurs on alternative hosts [37].
Other possible reasons for the combination of low vector competence and high PvR0 in the current study could include the highly heterogeneous HBR in human occupied forest landscapes. Such heterogeneity can be caused by deforestation level, presence of larval hotspots in the forest fringe, proximity of houses to the forest border, and human behaviour, all of which can increase mosquito–human contact. Furthermore, the field collections were conducted during the transition of the wet–dry season and in the dry season, when larval habitats have been shown to be more ecologically favourable to Ny. darlingi, thereby increasing female survival [54]. Consequently, the prevalence of P. vivax in the adult population is expected to be higher, as in [55].
Conclusions
This is the first study to use mathematical modelling approach to calculate the vectorial capacity of Ny. darlingi employing field-collected data on malaria incidence in Brazil. Results of mathematical modelling approach to quantify entomological potential and transmission intensity of malaria bolster the importance of Ny. darlingi in the P. vivax malaria cycle in rural settlements in the Brazilian Amazon. The estimated low vector competence of this species seems to be offset by its relatively high vectorial capacity, and its occurrence in the peridomestic environment. These factors, in addition to poor housing conditions and human behaviour, resulted in very high PvR0, evidence for intense and stable transmission in the Galo Velho settlement, Machadinho D’Oeste, Rondônia and in São Gabriel da Cachoeira, Amazonas. Variation in vectorial capacity and R0 may be the result of heterogeneities in the level of human exposure to mosquito bites rather than variation in vector populations.
Strategic planning for malaria control employing interventions, such as mass screening for parasite reservoirs using rapid diagnostic test, and effective anti-malarial drugs treatments will decrease infection duration, local incidence, infection incidence, parasite reservoirs, and transmission intensity. In addition, indoor residual spray and long-lasting insecticide nets will decrease human exposure to mosquito bites to some degree, shrinking the transmission in these and other Amazonian municipalities with similar determinants of malaria risk. However, if the entomological potential either persists or increases, imported infections will replenish parasite reservoirs, boosting malaria transmission in areas that are receptive for Plasmodium propagation.
Abbreviations
- API:
-
annual parasite incidence
- b t :
-
vector competence
- HLC:
-
human landing catch
- h t :
-
the daily malaria incidence
- R 0 :
-
basic reproduction number
- V Ct :
-
vectorial capacity
- SIVEP:
-
Sistemas de Informações de Vigilância Epidemiológica da Malaria
References
Shretta R, Liu J, Cotter C, Cohen J, Dolenz C, Makomva K, et al. Chapter 12, Malaria elimination and eradication. In: Holmes KK, Bertozzi S, Bloom BR, Jha P, editors. Major infectious diseases. 3rd ed. Washington (DC): The International Bank for Reconstruction and Development/The World Bank; 2017.
WHO. World malaria report 2018. Geneva: World Health Organization; 2018.
Grillet ME, Villegas L, Oletta JF, Tami A, Conn JE. Malaria in Venezuela requires response. Science. 2018;359:528.
Conn JE, Grillet ME, Correa M, Sallum MAM. Malaria transmission in South America—Present status and prospects for elimination, towards malaria elimination—a leap forward, Sylvie Manguin and Vas Dev, IntechOpen. https://doi.org/10.5772/intechopen.76964.
Almeida ACG, Kuehn A, Castro AJM, Vitor-Silva S, Figueiredo EFG, Brasil LW, et al. High proportions of asymptomatic and submicroscopic Plasmodium vivax infections in a peri-urban area of low transmission in the Brazilian Amazon. Parasit Vectors. 2018;11:194.
Recht J, Siqueira AM, Monteiro WM, Herrera SM, Herrera S, Lacerda MVG. Malaria in Brazil, Colombia, Peru and Venezuela: current challenges in malaria control and elimination. Malar J. 2017;16:273.
Cohen JM, Le Menach A, Pothin E, Eisele TP, Gething PW, Eckhoff PA, et al. Mapping multiple components of malaria risk for improved targeting of elimination interventions. Malar J. 2017;16:459.
Reiner RC Jr, Perkins TA, Barker CM, Niu T, Chaves LF, Ellis AM, et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J R Soc Interface. 2013;10:20120921.
Smith DL, Perkins TA, Reiner RC Jr, Barker CM, Niu T, Chaves LF, et al. Recasting the theory of mosquito-borne pathogen transmission dynamics and control. Trans R Soc Trop Med Hyg. 2014;108:185–97.
Elliott RC, Smith DL, Echodu D. Medical and entomological malarial interventions, a comparison and synergy of two control measures using a Ross/Macdonald model variant and open malaria simulation. Math Biosci. 2018;300:187–200.
Adde A, Roux E, Mangeas M, Dessay N, Nacher M, Dusfour I, et al. Dynamical mapping of Anopheles darlingi densities in a residual malaria transmission area of French Guiana by using remote sensing and meteorological data. PLoS ONE. 2016;11:e0164685.
Tucker Lima JM, Vittor A, Rifai S, Valle D. Does deforestation promote or inhibit malaria transmission in the Amazon? A systematic literature review and critical appraisal of current evidence. Philos Trans R Soc Lond B Biol Sci. 2017;372:1722.
Chaves LSM, Conn JE, López RVM, Sallum MAM. Abundance of impacted forest patches less than 5 km2 is a key driver of the incidence of malaria in Amazonian Brazil. Sci Rep. 2018;8:7077.
Massad E, Coutinho FA. Vectorial capacity, basic reproduction number, force of infection and all that: formal notation to complete and adjust their classical concepts and equations. Mem Inst Oswaldo Cruz. 2012;107:564–7.
Smith DL, Battle KE, Hay SI, Barker CM, Scott TW, McKenzie FE. Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012;8:e1002588.
Brady OJ, Godfray HC, Tatem AJ, Gething PW, Cohen JM, McKenzie FE, et al. Adult vector control, mosquito ecology and malaria transmission. Int Health. 2015;7:121–9.
Macdonald G. Theory of the eradication of malaria. Bull World Health Organ. 1956;15:369–87.
Ministério da Saúde do Brasil. Datasus. Sivep Malária. Sistema Eletrônico do Serviço de Informações ao Cidadão (e-SIC). 2018. https://esic.cgu.gov.br/sistema/site/index.aspx.
Bickersmith SA, Lainhart W, Moreno M, Chu VM, Vinetz JM, Conn JE. A sensitive, specific and reproducible real-time polymerase chain reaction method for detection of Plasmodium vivax and Plasmodium falciparum infection in field-collected anophelines. Mem Inst Oswaldo Cruz. 2015;110:573–6.
Laporta GZ, Burattini MN, Levy D, Fukuya LA, de Oliveira TM, Maselli LM, et al. Plasmodium falciparum in the southeastern Atlantic forest: a challenge to the bromeliad-malaria paradigm? Malar J. 2015;14:181.
Center for Disease Control (CDC, 2010). Malaria glossary of terms. http://definedterms.com/a/document/10617. Accessed 11 Oct 2018.
Ross R. The prevention of malaria. 2nd ed. London: John Murray; 1911.
Garrett-Jones C, World Health Organization. A method for estimating the man-biting rate/by C. Garrett-Jones. Geneva: World Health Organization; 1964. http://www.who.int/iris/handle/10665/65193.
Garrett-Jones C. The human blood index of malaria vectors in relation to epidemiological assessment. Bull World Health Organ. 1964;30:241–61.
Dietz K, Molineaux L, Thomas A. A malaria model tested in the African Savannah. Bull World Health Organ. 1974;50:347–57.
Dietz K, Molineaux L, Thomas A. The mathematical model of transmission. In: Molineaux L, Gramiccia G, editors. The Garki Project. Geneva: World Health Organization; 1980. p. 261–88.
Anderson RM, May RM. The population dynamics of microparasites and their invertebrate hosts. Phil Trans R Soc Lond B. 1981;291:451–524.
Moreno M, Tong C, Guzmán M, Chuquiyauri R, Llanos-Cuentas A, Rodriguez H, et al. Infection of laboratory-colonized Anopheles darlingi mosquitoes by Plasmodium vivax. Am J Trop Med Hyg. 2014;90:612–6.
Nassir E, Abdel-Muhsin AM, Suliaman S, Kenyon F, Kheir A, Geha H, et al. Impact of genetic complexity on longevity and gametocytogenesis of Plasmodium falciparum during the dry and transmission-free season of eastern Sudan. Int J Parasitol. 2005;35:49–55.
Tadei WP, Santos JMM, Costa WLD, Scarpassa VM. Biologia dos anofelinos amazônicos: XI. Ocorrência de espécies de Anopheles, dinâmica da transmissão e controle da malária na zona urbana de Ariquemes (Rondônia). Rev Inst Med Trop São Paulo. 1988;30:221–51.
Sinka MA, Rubio-Palis Y, Manguin S, Patil AP, Temperley WH, Gething PW, et al. The dominant Anopheles vectors of human malaria in the Americas: occurrence data, distribution maps and bionomic précis. Parasit Vectors. 2010;3:72.
Hiwat H, Bretas G. Ecology of Anopheles darlingi Root with respect to vector importance: a review. Parasit Vectors. 2011;4:177.
Moutinho PR, Gil LHS, Cruz RB, Ribolla PEM. Population dynamics, structure and behavior of Anopheles darlingi in a rural settlement in the Amazon rain forest of Acre, Brazil. Malar J. 2011;10:174.
Hiwat H, De Rijk M, Andriessen R, Koenraadt CJ, Takken W. Evaluation of methods for sampling the malaria vector Anopheles darlingi (Diptera, Culicidae) in Suriname and the relation with its biting behavior. J Med Entomol. 2011;48:1039–46.
Rubio-Palis Y, Moreno JE, Sánchez V, Estrada Y, Anaya W, Bevilacqua M, et al. Can Mosquito Magnet® substitute for human-landing catches to sample anopheline populations? Mem Inst Oswaldo Cruz. 2012;107:546–9.
Lima JB, Rosa-Freitas MG, Rodovalho CM, Santos F, Lourenço-de-Oliveira R. Is there an efficient trap or collection method for sampling Anopheles darlingi and other malaria vectors that can describe the essential parameters affecting transmission dynamics as effectively as human landing catches? Mem Inst Oswaldo Cruz. 2014;109:685–705.
Moreno M, Saavedra MP, Bickersmith SA, Lainhart W, Tong C, Alava F, et al. Implications for changes in Anopheles darlingi biting behaviour in three communities in the peri-Iquitos region of Amazonian Peru. Malar J. 2015;14:290.
Prussing C, Moreno M, Saavedra MP, Bickersmith SA, Gamboa D, Alava F, et al. Decreasing proportion of Anopheles darlingi biting outdoors between long-lasting insecticidal net distributions in peri-Iquitos, Amazonian Peru. Malar J. 2018;17:86.
de Castro MC, Sawyer DO, Singer BH. Spatial patterns of malaria in the Amazon: implications for surveillance and targeted interventions. Health Place. 2007;13:368–80.
Barros FS, Arruda ME, Gurgel HC, Honório NA. Spatial clustering and longitudinal variation of Anopheles darlingi (Diptera: Culicidae) larvae in a river of the Amazon: the importance of the forest fringe and of obstructions to flow in frontier malaria. Bull Entomol Res. 2011;101:643–58.
de Castro MC, Monte-Mór RL, Sawyer DO, Singer BH. Malaria risk on the Amazon frontier. Proc Natl Acad Sci USA. 2006;103:2452–7.
de Barros FS, Honório NA, Arruda ME. Temporal and spatial distribution of malaria within an agricultural settlement of the Brazilian Amazon. J Vector Ecol. 2011;36:159–69.
Rufalco-Moutinho P, Schweigmann N, Bergamaschi DP, Mureb Sallum MA. Larval habitats of Anopheles species in a rural settlement on the malaria frontier of southwest Amazon, Brazil. Acta Trop. 2016;164:243–58.
Schoeler GB, Flores-Mendoza C, Fernández R, Davila JR, Zyzak M. Geographical distribution of Anopheles darlingi in the Amazon Basin region of Peru. J Am Mosq Control Assoc. 2003;19:286–96.
Flores-Mendoza C, Fernández R, Escobedo-Vargas KS, Vela-Perez Q, Schoeler GB. Natural Plasmodium infections in Anopheles darlingi and Anopheles benarrochi (Diptera: Culicidae) from Eastern Peru. J Med Entomol. 2004;41:489–94.
Oliveira-Ferreira J, Lourenço-de-Oliveira R, Teva A, Dean M, Daniel-Ribeiro CT. Natural malaria infections in anophelines in Rondonia state, Brazilian Amazon. Am J Trop Med Hyg. 1990;43:6–10.
da Silva-Vasconcelos A, Kató MY, Mourão EN, de Souza RT, Lacerda RN, Sibajev A, et al. Biting indices, host-seeking activity and natural infection rates of anopheline species in Boa Vista, Roraima, Brazil from 1996 to 1998. Mem Inst Oswaldo Cruz. 2002;97:151–61.
Póvoa MM, de Souza RT, Lacerda RN, Rosa ES, Galiza D, de Souza JR, et al. The importance of Anopheles albitarsis E and An. darlingi in human malaria transmission in Boa Vista, state of Roraima, Brazil. Mem Inst Oswaldo Cruz. 2006;101:163–8.
Taylor LH. Infection rates in, and the number of Plasmodium falciparum genotypes carried by Anopheles mosquitoes in Tanzania. Ann Trop Med Parasit. 1999;93:659–62.
Hay SI, Smith DL, Snow RW. Measuring malaria endemicity from intense to interrupted transmission. Lancet Infect Dis. 2008;8:369–78.
Klein TA, Lima JB, Tang AT. Biting behavior of Anopheles mosquitoes in Costa Marques, Rondonia, Brazil. Rev Soc Bras Med Trop. 1991;24:13–20.
Conn JE, Wilkerson RC, Segura MN, de Souza RT, Schlichting CD, Wirtz RA, Póvoa MM. Emergence of a new neotropical malaria vector facilitated by human migration and changes in land use. Am J Trop Med Hyg. 2002;66:18–22.
Klein TA, Lima JB, Tada MS, Miller R. Comparative susceptibility of anopheline mosquitoes in Rondonia, Brazil to infection by Plasmodium vivax. Am J Trop Med Hyg. 1991;45:463–70.
Barros FS, Honório NA. Deforestation and malaria on the Amazon frontier: larval clustering of Anopheles darlingi (Diptera: Culicidae) determines focal distribution of malaria. Am J Trop Med Hyg. 2015;93:939–53.
Barros FS, Honório NA, Arruda ME. Survivorship of Anopheles darlingi (Diptera: Culicidae) in relation with malaria incidence in the Brazilian Amazon. PLoS ONE. 2011;6:e22388.
Authors’ contributions
EM, MAMS and JEC conceived of the study. EM, CJS, LY, LO conducted all mathematical analyses. MAMS, ESB, GZL, LSC planned and conducted the field collections, including the human landing catches. EF, GM provided epidemiological malaria data and orientation for the localities for field collections. MAMS identified field specimens. SB and TMPO conducted the laboratory experiments. MAMS, EM, and JEC wrote the manuscript, with contributions to the interpretation of results from all authors. All authors contributed to the final draft of the manuscript. All authors read and approved the final manuscript.
Acknowledgements
MAMS is indebted and thankful to Caio Cesar Moreira and Denise Cristina Sant’Ana for their help for arranging material for field trips to the Amazon and to Roberto Tetsuro Nakaoka for proving invaluable information about field collections in Machadinho D’Oeste, Rondônia. Authors are in debt to the staff of the municipalities responsible for malaria control for providing useful information that guided field collections in Cruzeiro do Sul, Mâncio Lima, Lábrea, Machadinho D’Oeste and São Gabriel da Cachoeira. Authors greatly appreciate all anonymous inhabitants of the rural settlements, and the staff of the Vector Malaria Control of the municipalities, who generously helped authors to contact the communities where malaria is a trap for maintaining poverty, inequality and human suffering. Without their help this study would not have been possible.
Competing interests
The authors declare that they have no competing interests.
Availability of data and materials
Data used in the manuscript will be freely available to any scientist wishing to use them for non-commercial purposes upon request, by the corresponding author. In addition, the full data will be publicly available after publication of a series of articles that are in preparation.
Consent for publication
Not applicable.
Ethics approval and consent to participate
Not applicable.
Funding
This work has been partially funded by the National Institutes of Health, USA, Grant R01 AI110112 to JEC and MAS; Fundação de Amparo à Pesquisa do Estado de São Paulo—FAPESP Grant No. 2014/26229-7 to MAMS and EM; Conselho Nacional de Pesquisa—CNPq no. 301877/2016-5 to MAMS; FAPESP Grant No. 2014/09774-1 to GZL; ZikaPLAN, funded by the European Union’s Horizon 2020 research and innovation programme, Grant No. 734584.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Additional files
Additional file 1.
Distribution of malaria according to epidemiological week (EPI) in five municipalities of the Amazonian states, 2014–2018, Brazil.
Additional file 2.
The raw data of Plasmodium vivax malaria incidence in the five municipalities studied in Brazilian Amazon, and the parameters used in the fitting procedures are provided. These data do not include Plasmodium falciparum malaria.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Sallum, M.A.M., Conn, J.E., Bergo, E.S. et al. Vector competence, vectorial capacity of Nyssorhynchus darlingi and the basic reproduction number of Plasmodium vivax in agricultural settlements in the Amazonian Region of Brazil. Malar J 18, 117 (2019). https://doi.org/10.1186/s12936-019-2753-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12936-019-2753-7