Abstract
Background
Recent publications have reported follow-up of the RTS,S/AS01 malaria vaccine candidate Phase III trials at 11 African sites for 32 months (or longer). This includes site- and time-specific estimates of incidence and efficacy against clinical disease with four different vaccination schedules. These data allow estimation of the time-course of protection against infection associated with two different ages of vaccination, both with and without a booster dose.
Methods
Using an ensemble of individual-based stochastic models, each trial cohort in the Phase III trial was simulated assuming many different hypothetical profiles for the vaccine efficacy against infection in time, for both the primary course and boosting dose and including the potential for either exponential or non-exponential decay. The underlying profile of protection was determined by Bayesian fitting of these model predictions to the site- and time-specific incidence of clinical malaria over 32 months (or longer) of follow-up. Using the same stochastic models, projections of clinical efficacy in each of the sites were modelled and compared to available observed trial data.
Results
The initial protection of RTS,S immediately following three doses is estimated as providing an efficacy against infection of 65 % (when immunizing infants aged 6–12 weeks old) and 91 % (immunizing children aged 5–17 months old at first vaccination). This protection decays relatively rapidly, with an approximately exponential decay for the 6–12 weeks old cohort (with a half-life of 7.2 months); for the 5–17 months old cohort a biphasic decay with a similar half-life is predicted, with an initial rapid decay followed by a slower decay. The boosting dose was estimated to return protection to an efficacy against infection of 50–55 % for both cohorts. Estimates of clinical efficacy by trial site are consistent with those reported in the trial for all cohorts.
Conclusions
The site- and time-specific clinical observations from the RTS,S/AS01 trial data allowed a reasonably precise estimation of the underlying vaccine protection against infection which is consistent with common underlying efficacy and decay rates across the trial sites. This calibration suggests that the decay in efficacy against clinical disease is more rapid than that against infection because of age-shifts in the incidence of disease. The dynamical models predict that clinical effectiveness will continue to decay and that likely effects beyond the time-scale of the trial will be small.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Background
Malaria continues to cause significant burden and mortality worldwide with an estimated 580,000 deaths each year [1]. This represents large reductions in malaria mortality from 2000 levels due to large-scale roll-out of insecticide-treated nets and improved access to malaria treatment. However, new tools, such as malaria vaccines, may play a role in further reducing burden and preventing infection. The final results of Phase III clinical trials of malaria vaccine RTS,S were recently published [2], demonstrating efficacy against clinical disease in the two age groups that were vaccinated in 11 trial sites across malaria-endemic Africa (in the presence of high insecticide-treated net (ITN) usage and high quality access to care). The observed proportionate reduction in incidence of clinical malaria comparing the vaccinated and the control group, called here the efficacy against clinical disease, declined over time from 60 % during the first 6 months to 16 % during months 21–32 of follow-up in children aged 5–17 months old; in infants aged 6–12 weeks, the efficacy declined from 44 to 8 % during the same periods. For the entire follow-up period of 32 months, observed efficacy against clinical malaria was 35 % (95 % CI 31–40 %) in children and 20 % (95 % CI 14–27 %) in infants [2]. A boosting dose, given 18 months after the primary course of three doses, extended protection but not to the level seen in the 6 months following the primary course. Efficacy against clinical malaria in the booster cohorts was 44 % (95 % CI 40–48 %) in children and 28 % (95 % CI 22–33 %) in infants over the entire follow-up period of 32 months, but in months 21–32 of the trial (immediately after boosting) vaccine efficacy of 38 % for children and 27 % for infants was observed.
This trial provides estimates of efficacy against clinical malaria, but does not provide direct estimates of the underlying protection against infection or of the dynamics of protection over time. Mathematical models of malaria dynamics are needed to infer the underlying level of protection against infection, allowing for the dynamics of pathogenesis and of the acquisition of immunity. When calibrated with trial data, such models can be used to elucidate how setting specific factors (such as the level of exposure to malaria infection) modify these dynamics to give rise to the observed clinical efficacy.
RTS,S acts by inducing an immune response against the circumsporozoite protein (CSP) of the sporozoites of the Plasmodium parasite. When high immune responses are achieved, this reduces the chances of liver infection and subsequent blood-stage infection, and hence clinical malaria. Partial immunity to the different life stages of the malaria parasite within-host is induced naturally by repeated malaria infection, and thus non-vaccinated individuals more rapidly acquire immunity to the blood-stage parasites causing clinical illness. RTS,S, or indeed any other partially protective malaria infection blocking intervention aimed at infants and young children, will thus give rise to age shifts of burden and increased susceptibility to infection in older children [3, 4].
Previous analysis from the 18-month follow-up of RTS,S Phase III results [5] predicted that RTS,S has a high initial efficacy against infection (greater than 80 % in children vaccinated between five and 17 months and 65 % in infants vaccinated between 6 and 12 weeks), with an exponential half-life of decay of efficacy against infection of around 1 year [6]. However, the length of follow-up from the trial results was too short to determine if exponential decay was the most likely profile of decay of protection. Analysis of RTS,S Phase II antibody data indicated that biphasic exponential dynamics, with a quick decay followed by a long decay, fit the data better than a single exponential [7]. More recently, observations of incidence and efficacy in the boosting cohorts have become available and can be used to determine the underlying protection against infection offered by boosting doses [2].
This paper extends previous analysis [6] using the final published results of RTS,S in Phase III studies [2] to determine the time course of protection of RTS,S following a primary course of three doses in infants and children and following a boosting dose at 18 months post third dose. The temporal profile of RTS,S efficacy against infection is estimated using the malaria epidemiology microsimulation platform OpenMalaria [8], the observed incidence in the vaccinated and control cohorts and Bayesian Markov Chain Monte Carlo (MCMC) methods. This further allows use of OpenMalaria simulations to project the efficacy against clinical and severe disease in each of the trial sites for follow-up longer than that so far published.
Methods
RTS,S trial cohorts and data
The number of infants or children in the intention-to-treat analysis of the Phase III RTS,S trial, along with the recorded number of cases of clinical malaria, primary case definition, at 3 monthly time points per trial site, were used in this study. All data were previously published in [2].
Vaccine trial simulations of RTS,S Phase III clinical trials with OpenMalaria
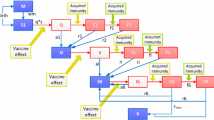
OpenMalaria is an individual-based, stochastic model of malaria epidemiology and control [8, 9] that includes model components of malaria in mosquitoes [10], dynamics of infection to humans [11], blood-stage parasite densities [12], infectiousness to mosquitoes [13], incidence of morbidity including severe, and hospitalization and mortality [14, 15]. Pre-erythrocytic and blood-stage immunity comprise separate sub-models, with blood-stage immunity predominating as infection-blocking immunity occurs only in those with very high cumulative exposure [12]. The ensemble of six model variants, described in Table 1, include different assumptions for decay of natural immunity, greater within-host variability between infection and entomological exposure and heterogeneity [8].
Each arm of the vaccine trial was explicitly simulated with an OpenMalaria ensemble of six models [8] (Table 1). Similar to previous analysis, predictions of clinical trial outcomes were calculated via weighted averages of a large number of simulations [6]. The simulations covered a wide range of vaccine profile characteristics, deployed across a range of health system and transmission settings of the trial sites. The weights applied to each simulation are dependent on the trial-specific data and on vaccine properties for fitting.
Six databases of simulations from OpenMalaria were created, two for baseline (control cohorts 6–12 weeks and 5–17 months) and four for vaccine impact predictions (boost and non-boosting schedules for 6–12 weeks and 5–17 months) over a range of assumptions on transmission exposures [entomological inoculation rates (EIR)], timing of vaccination due to seasonality profile, range of access to effective treatment for uncomplicated cases, and for many hypothetical vaccine efficacy profiles (initial efficacy against infection, decay shape and boosting efficacy against infection, with boosting efficacy defined as the overall efficacy reached by an additional fourth vaccine dose, not incremental efficacy addition to the primary course). Each database was a complete factorial combination of all levels of each variable listed in Table 1, with a database constructed for each of the 6–12 weeks cohorts with and without booster, 5–17 months cohorts with and without booster, and the no-vaccine cohorts. This resulted in over 500,000 simulations when replicates with different stochastic initializations were counted. Outputs from the simulations were recorded at 3-monthly intervals, for 3-monthly age groups, with vaccination occurring at the ages specified in Table 1. For each simulation the numbers of uncomplicated cases, severe cases, direct malaria deaths, indirect malaria deaths, sequelae events, first-line, second-line and third-line treatments given, hospitalized cases resulting in recovery, hospitalized cases that resulted in sequelae and hospitalized cases that resulted in death were recorded, to allow incidence calculations to compare to trial data.
Predictions of incidence for each cohort and clinical efficacy in time per vaccination schedule in each trial site were obtained via weighted averages over all simulations in the appropriate database (see [6] for full methods). Predictions comprise mean weighted averages with an accompanying range constructed from the 95 % prediction interval over the weighted averages for all models and stochastic runs, with each model variant equally weighted. The prediction intervals thus capture both structural and stochastic uncertainty.
Trial-specific parameter weights for transmission and access to care were pre-determined or estimated by fitting to the trial data. Separate estimates were made for each trial site of the levels of access to treatment and of the exposure (EIR). This entailed fitting to the control incidence disaggregated into 3-monthly time intervals and the control cohort at baseline in the trial site.
The posterior densities of the prevalence in 2–10 years olds (PfPR2–10), estimated from a geostatistical model at 5 × 5 km resolution by the Malaria Atlas Project 2010 (MAP) [16], were used to capture effects of within-site heterogeneity in transmission. A previously published algorithm using OpenMalaria [17] was used to derive distributions of EIR for each trial site, as functions of the PfPR2–10 data, access to treatment data for the same geographic area estimated from demographic and health surveys (DHS), and the population of each pixel derived from the demographic population surfaces [18] (Table 2). For simulation of the trial, these EIR distributions were scaled so that the average prevalence predicted by OpenMalaria matched the baseline prevalence measured in each trial site and each site was then treated as having a mixture of transmission intensities corresponding to this scaled EIR distribution. In the trial simulations, access to care for each site was assigned the value required to recover the incidence of diagnosed clinical malaria reported in the control (non-vaccine) arms.
Vaccine efficacy against infection and decay
The action of RTS,S (or other pre-erythrocytic vaccines) in OpenMalaria is to prevent new infections, with the proportion of blood-stage infections averted referred to as vaccine efficacy against infection. This is different from the efficacy in averting clinical episodes as reported in the Phase III clinical trials. The time course of efficacy against infection can be described by several possible decay functions in OpenMalaria [19]. Different Weibull decay function curves are investigated for describing the waning protection of RTS,S by an initial value of the efficacy against infection \(\varepsilon_{0}\), a half-life L, and a shape parameter, k. The Weibull decay function for efficacy against infection, ɛ(t), at time t, takes the.
When k is 1, an exponential decay of efficacy against infection is obtained. For k < 1, the initial decay is faster than exponential and then slower than exponential after the time equivalent to half-life is reached, this is similar to a bi-phasic like decay, with a sharp decline (quick decay) in efficacy followed by a slower decay. For k > 1, the curves is a slow decay of efficacy against infection until the time equivalent to half-life L, and then a much faster decay.
Determining vaccine properties from Phase III clinical trial data
Using Bayesian MCMC methods, comparing simulated incidence and Phase III trial incidences, the efficacy profile for each cohort was determined in terms of initial efficacy against infection following the primary schedule of three doses. This profile comprises the half-life of decay of efficacy against infection, the shape parameter describing the waning profile, and the efficacy against infection following a boosting dose. Models were simultaneously fit to the control and vaccinated incidence from each trial site for the primary case definition, 3-monthly or 6-monthly aggregated intention-to-treat (ITT). Data from the Kilifi and Manhica were not used for fitting of vaccine properties because of challenges related to missing data: instead, the predictions for these sites provided an out-of-sample check on the performance of the fitting algorithm.
As previously described in [6], a Bayesian MCMC approach was used to estimate vaccine properties, site-specific access to care, and the extent of within-site variation in clinical disease (number of episodes per individual for a defined time period). The observed clinical data (disease rates in the control and vaccinated groups at each time point) are assumed to be normally distributed about the logarithm of their predicted values for a given set of parameters. i.e.:
where Yt,i is the observed disease rate (for control or vaccinated) at time t and trial site i, \({\hat{{\mu }}}_{t,i}\) is the weighted model prediction for the equivalent outcome at time t and site i, θ represents the parameters being fitted (vaccine properties and access to care), σ i is the standard-deviation for trial site i, \({\hat{{\mu }}}_{t,i}\), is the model prediction, obtained as the weighted average of simulated disease rates from the databases of vaccine cohort predictions from OpenMalaria (Table 1). The weights for site i were assigned to give the pre-determined distribution of EIR values representing malaria exposure in that site while an MCMC algorithm was used to sample parameters and estimate the weights for efficacy, half-life, decay shape and the access to care parameter.
Vaccine parameters for each age of vaccination cohort were fitted separately, so that independent parameters for the time course of vaccine efficacy against infection for the primary schedule were obtained. Vaccine parameters were assumed to take the same value for each site. To test robustness of the models, models were first fitted to aggregated 6-monthly observed incidence data per site and subsequently to the 3-monthly aggregated data. Parameterizating was also done assuming both exponential decay (Weibull decay function shape parameter k = 1) and also allowing the decay shape parameter to vary.
Two MCMC chains with very different initial conditions for efficacy, access to care, decay shape and half-life were used for each fitted model. Uniform [0, 1] priors were used for all parameters except the half-life of vaccine efficacy decay, which was assigned a Uniform [0, 5] years prior, with non-informative (uniform) priors for all parameters. Posterior distributions were sampled for each of the fitted parameters (6–12 weeks initial efficacy against infection, 5–17 months initial efficacy against infection, vaccine half-life of decay, decay shape parameter, within site variation against clinical disease and site-specific access to care).
Following determination of the vaccine efficacy profile of the primary course, the boost efficacy was obtained via Bayesian MCMC in a similar manner. Only the initial efficacy against infection as a result of a boosting dose was fitted, assuming the same decay shape as for the primary course (exponential or best fit when fitting Weibull decay parameter k).
Predictions of clinical disease efficacy beyond the trial follow-up
Clinical efficacy beyond the trial follow-up of 32 months was projected using the same model weighting (and hence final vaccine profile) as estimated from the trial data.
Results
Characteristics of trial sites
There was considerable variation between the sites in average transmission levels as estimated from the MAP surfaces, with substantial local heterogeneity within each site (Table 2). However, the baseline EIR in each site was generally lower than the prediction from MAP, as well as spanning a smaller range across the sites than when estimated from MAP. Similarly, the estimated access to care derived from the DHS was lower than the estimates derived by comparing model predictions of incidence with recorded events in the control arm of the trial (Table 2) [6].
We conjecture that this difference arises from better health care service provision in the study sites, than neighbouring areas. Both MAP PfPR2-10 and DHS-based estimates borrow information from adjacent geographical areas, and the sites were necessarily centred around high-quality health facilities with linked research infrastructure, and thus have unusually good access to both preventive and curative interventions.
RTS,S vaccine efficacy against infection, time course for primary schedule of three doses
Regardless of assumptions concerning the functional form of decay of efficacy, the initial protection of the RTS,S vaccine in children 5–17 months is estimated to be high (similar to previous analysis). Fitting to 3-monthly incidence data and allowing decay to be either exponential or non-exponential the estimated efficacy against infection immediately following third dose was 91.1 (95 % CI 74.5–99.7 %) for children vaccinated between 5 and 17 months at first dose (Table 3; Fig. 1a). In infants vaccinated 6–12 weeks the initial efficacy against infection was 64.9 % (95 % CI 44.0–83.2 %) (Table 3; Fig. 1a). Results were similar when fitting to 6-monthly decay (Additional file 1: Table S1). Models were fit to the clinical incidence in both control and vaccinated cohorts (results shown in Additional file 1: Figures S1, S2, S3, S4), with calculated vaccine efficacy for the best fitted models assuming exponential and Weibull decay are shown in Fig. 2.
Posterior distributions of parameters for vaccine efficacy profiles (assuming Weibull decay function, fitted to trial data at 3-monthly periods). Colour green indicates 6–12 weeks cohort, and pink the 5–17 months cohort. a Vaccine initial efficacy against infection; b half-life of decay in efficacy against infection; c Weibull decay function shape parameters; d boost efficacy against infection
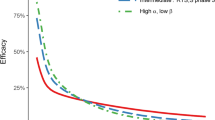
Observed and predicted efficacy against clinical disease for 3-monthly periods. Field and predicted estimates of clinical efficacy at each 3-month follow-up for a the 6–12 weeks without booster; b 5–17 months cohort without booster, by the 9 trial site used in the fitting (excludes Kilifi and Manhica). Reported efficacy (mean and 95 % CI) in the trial site is indicated by black circles. Prediction estimates (mean and 95 % prediction intervals) are shown in colour for different fitted models, orange assuming exponential decay and blue fitting for decay shape
Assuming exponential decay, the half-life of protection was approximately 7–8 months for both cohorts (Table 3; Fig. 1b and Additional file 1: Table S1). When allowing decay to be non-exponential, half-life of decay against infection was also around 7 months (95 % CI 6–10 months for both cohorts), with decay shapes for the 5–17 months cohorts k = 0.69 (95 % CI 0.54–0.9) indicating a quick decay followed by a longer decay. For the 6–12 weeks cohort the prediction is closer to exponential k = 0.84 (95 % CI 0.64–0.99).
Boosting dose efficacy against infection
The efficacy against infection of the single boosting dose given 18 months following third dose was estimated to be lower than that immediately following the final dose of the primary course, with estimates of 49 % (95 % CI 32–68.6 %) for children 5–17 months and 55.2 % (95 % CI 34.5–73.1 %) for infants 6–12 weeks (Table 3; Fig. 1d). These estimates assume that the half-life and decay of the boosting dose were the same as fitted for the primary course.
Predictions of efficacy against clinical disease
Figures 3, 4, 5 and 6 show projections of the efficacy against clinical disease over the time periods of the trial follow-up and beyond the course of the trial (longer follow-up than shown in Fig. 2), based on the best-fitting vaccine profile (assuming Weibull decay function). Efficacy against clinical disease decays more rapidly than efficacy against infection. This is because the reduced build-up of natural blood-stage immunity resulting from protection against infection has the effect of delaying, rather than averting some of the clinical incidence in the vaccine arm. There is no such age shifting of infection events because these models assume natural pre-erythrocytic immunity to be negligible. By 3 years after the start of the trial, the efficacy against infection in the 5–17 months cohort is predicted to be close to zero, irrespective of whether a booster dose is included in the schedule (Fig. 4).
Predicted and observed efficacy against clinical disease by 3-monthly periods by trial site for the 5–17 months cohort with booster using best-fitted vaccine profile. Reported efficacy (mean and 95 % CI) in the trial site is indicated by black circles. Prediction estimates in purple (median and 95 % CI)
Predicted and observed efficacy against clinical disease by three-monthly periods by trial site for the 6–12 weeks cohort with booster using best-fitted vaccine profile. Reported efficacy (mean and 95 % CI) in the trial site is indicated by black circles. Prediction estimates in purple (median and 95 % CI)
Overall protection against clinical disease at any time point following the primary course is predicted to be positive over all trial sites (Fig. 7) and potentially close to zero at very long follow-up for the two sites with highest transmission, Siaya and Nanoro (Fig. 7; Additional file 1: Figures S5, S6) This indicates, despite the potential for age shifting, a sustained benefit over the vaccinated population up to 4 years following the primary course.
Predicted cumulative vaccine efficacy against clinical disease over time (in years post dose 3) over all trial sites for the a 5–17 months cohort and b 6–12 weeks cohort with and without booster. The solid lines show the predicted efficacy with the booster schedule and the dashed lines the predicted efficacy with the non-booster schedule
Discussion
Clinical efficacy measured in field trials is a key source of information about the likely benefit of deploying preventive interventions against malaria. Assessment of the impact of intervention programmes also needs to consider other factors, including the disease burden in target groups, the coverage achievable, the extent of protection extended to the rest of the population, and, importantly, both the magnitude and duration of effect. Mathematical models of malaria dynamics can be used to integrate information about all of these factors to determine duration of effects and subsequently the prediction of public health impact.
The RTS,S vaccine is currently the focus of decision-making by WHO, and depending on their recommendation, other stakeholders such as Gavi, the vaccine alliance, and national malaria control programmes will also need to make decisions concerning possible implementation. Such evidence-based policy decisions about partially protective vaccines need to take into account both trial data and what is known about malaria epidemiology and health systems (including vaccination programmes) from other sources. The recently completed Phase III trial of RTS,S has provided a substantial amount of data on its effects on clinical incidence in vaccinated children over a 32 months or longer follow-up period. Several different simulation models have been parameterized to fit the diverse outcomes of many previous field studies of Plasmodium falciparum to capture the collective knowledge of malaria epidemiologists about malaria dynamics [8, 9, 20–23]. Other publications describe how these models have been linked with data from other sources on vaccination coverage in endemic countries, and malaria disease burden, to project public health impact of RTS,S vaccination programmes, including its impact on outcomes, notably severe disease and death, for which the trial data taken in isolation were not sufficiently powered to provide robust estimates [6, 24, 25].
All models need to take into account that the primary effect of RTS,S is on infection, not on clinical outcomes. RTS,S acts by stimulating an immune response against the CSP of Plasmodium falciparum and potentially preventing an infection [26], and therefore its effects on pathogenesis and clinical incidence are indirect. The observed trial results of incidence in the control and vaccinated arms depend on the antibody and immunity longevity and response, but also on a number of factors, including the health system capacity to treat clinical cases, exposure of children to infectious mosquitoes, as well as the dynamical interplay between immunity acquisition, immunity delay, and subsequent effects on clinical and severe disease burden by age. In spite of these complexities, results of clinical incidence and clinical efficacy from the trial can be used, along with data from other field studies and dynamic malaria models, to infer the underlying protection of the vaccine and thus make extrapolations to population effects if the vaccine is recommended.
In this paper, both the characteristics of the vaccine and characteristics of each trial site, such as exposure and treatment levels, were treated as weighted averages of a large number of model realizations [6]. Bayesian fitting (via MCMC algorithms) of model predictions to observed clinical incidence in the cohorts estimates the weights of the vaccine characteristics. This fitting process considers both the stochasticity in the models and the imprecision in the data for the fitting process and uncertainty around the predictions. As investigated previously [6], the most parsimonious model assumes the extent and duration of the induced protection against infection to be the same in all sites, fits the data well.
In general, the fit to the temporal profiles of incidence in the different sites was good (Additional file 1: Figures S1, S2, S3, S4), with simulated efficacy against clinical disease values close to the values measured in the trial (Figs. 2, 3, 4, 5 6), but in some sites (in particular Lambarene, Lilongwe, Korogwe, and Bagamoyo) there was considerable variation in efficacy between time periods (presumably because of random variation), so the relatively smooth trends in incidence predicted by the models were not observed. The tendency for the observed efficacy against clinical disease to be less in higher transmission sites is explained by the dynamics of immune acquisition against repeated infections, and does not require any site-specific assumptions about how the vaccine works.
The results here indicate that following the third dose the initial protection from RTS,S is close to complete in the 5–17 months cohort (91.1 % with the maximum possible value of 100 %), but substantially less than that in infants 6–12 weeks with much larger variation (64 %, Fig. 1). The most likely explanation for this age difference would seem to be that maternal immunity contributes to protection in infants, but that it has no synergistic effect with RTS,S, so that by averting some of the infections that would have been prevented by RTS,S, such as those with lower numbers of sporozoites, it leads to a lower efficacy against clinical disease that can be unambiguously attributed to the vaccine. Immune interference due to administration of RTS,S/AS01 at the same time as EPI vaccines could hypothetically also have an effect [2]. Despite high initial protection against infection in children, the protection in both groups waned quickly, leading to quick waning in efficacy against clinical disease. The decay in efficacy against clinical malaria is due to both decay of immunity for protection against sporozoites and acquisition of natural immunity against clinical disease in the control cohort.
The half-life of decay of efficacy against infection was very similar for the two age groups, but while the fitted curve was similar to an exponential decay in the infants (Fig. 2a), a Weibull decay function with fast decay, followed by longer decay, fits better with the 5–17 months old cohort (assessed via Deviance Information Criterion for nested models, as done previously [6] ). This corresponded to higher efficacy against infection and against clinical disease (Fig. 3) over most of the follow-up period for the older cohort compared to the infants 6–12 weeks (Fig. 5).
The underlying protection gained by a single boosting dose 18 months following the primary course was similar for both cohorts, at around 50 %, but not as high as the initial protection from the final dose of the primary course. This suggests that immune memory cells have shorter duration than normal [27]. The current analysis here assumes that the likely decay of the additional dose is similar for the boosting dose to that for the primary course.
Projections of impact towards the end of the trial and beyond indicate that in low transmission sites the protection against clinical disease is continued. For higher transmission, low clinical efficacy and some age-shifting of clinical incidence is predicted, with such shifting partially observed in the 4-year follow-up of one Phase II trial of RTS,S [28]. Overall, a net positive benefit is predicted up to 4 years after the trial starts, despite some age shifting of events in higher transmission sites. Following any positive WHO recommendation, vaccination of age groups outside those considered in the trial and vaccination covering larger proportions of the population in low transmission settings, will be worth considering to assess indirect effects on transmission and possible local interruption of transmission [29].
Conclusion
As previously shown [6, 30] and confirmed here with comprehensive analysis of the latest trial results, protection against infection by RTS,S is initially high, but decays quickly and results in a moderately efficacious vaccine against malaria clinical disease [2]. Despite being moderately efficacious, there is much potential for RTS,S to play a role in averting disease and protecting young children most at risk [6]. A recommendation on the use of RTS,S is pending and will need to consider how the underlying protection of the vaccine against infection translates into averted disease morbidity and mortality in more diverse transmission settings and populations than the trial. Models have been carefully calibrated to historical data, and recently RTS,S vaccine action within these models has been rigorously calibrated given availability of trial data to modelling groups [2]. The careful and rigorous calibration of underlying effect of RTS,S sets a high standard for the use of models in future decision making on interventions against malaria (and other infectious diseases), and is essential for sound quantitative prediction of public health burden and cost effectiveness. However, uncertainty in such predictions is unavoidable, especially for more downstream events such as severe disease and mortality. For these outcomes there are only limited calibration data available, if at all, and varying incidence and efficacy patterns across the trial sites is likely due to variation driven by local factors, such as patterns of co-morbidities.
References
World Health Organization. World Malaria Report 2013. Geneva: World Health Organization; 2014.
RTSS Clinical Trials Partnership. Efficacy and safety of RTS,S/AS01 malaria vaccine with or without a booster dose in infants and children in Africa: final results of a phase 3, individually randomised, controlled trial. Lancet. 2015;386:31–45.
Pemberton-Ross P, Smith TA, Hodel EM, Kay K, Penny MA. Age-shifting in malaria incidence as a result of induced immunological deficit: a simulation study. Malar J. 2015;14:287.
Coleman PG, Perry BD, Woolhouse ME. Endemic stability–a veterinary idea applied to human public health. Lancet. 2001;357:1284–6.
The RTSS Clinical Trials Partnership. Efficacy and safety of the RTS,S/AS01 malaria vaccine during 18 months after vaccination: a phase 3 randomized, controlled trial in children and young infants at 11 African sites. PLoS Med. 2014;2014(11):e1001685.
Penny MA, Galactionova K, Tarantino M, Tanner M, Smith TA. The public health impact of malaria vaccine RTS,S in malaria endemic Africa: country-specific predictions using 18 month follow-up Phase III data and simulation models. BMC Med. 2015;13:170.
White MT, Bejon P, Olotu A, Griffin JT, Bojang K, Lusingu J, Salim N, Abdulla S, Otsyula N, Agnandji ST, et al. A combined analysis of immunogenicity, antibody kinetics and vaccine efficacy from phase 2 trials of the RTS,S malaria vaccine. BMC Med. 2014;12:117.
Smith T, Ross A, Maire N, Chitnis N, Studer A, Hardy D, Brooks A, Penny M, Tanner M. Ensemble modeling of the likely public health impact of a pre-erythrocytic malaria vaccine. PLoS Med. 2012;9:44.
Smith T, Killeen GF, Maire N, Ross A, Molineaux L, Tediosi F, Hutton G, Utzinger J, Dietz K, Tanner M. Mathematical modeling of the impact of malaria vaccines on the clinical epidemiology and natural history of Plasmodium falciparum malaria: overview. Am J Trop Med Hyg. 2006;75:1–10.
Chitnis N, Hardy D, Smith T. A periodically-forced mathematical model for the seasonal dynamics of malaria in mosquitoes. Bull Math Biol. 2012;74:1098–124.
Smith T, Maire N, Dietz K, Killeen GF, Vounatsou P, Molineaux L, Tanner M. Relationship between the entomologic inoculation rate and the force of infection for Plasmodium falciparum malaria. Am J Trop Med Hyg. 2006;75:11–8.
Maire N, Smith T, Ross A, Owusu-Agyei S, Dietz K, Molineaux L. A model for natural immunity to asexual blood stages of Plasmodium falciparum malaria in endemic areas. Am J Trop Med Hyg. 2006;75:19–31.
Ross A, Killeen GF, Smith T. Relationships of host infectivity to mosquitoes and asexual parasite density in Plasmodium falciparum. Am J Trop Med Hyg. 2006;75(Suppl 2):32–7.
Ross A, Maire N, Molineaux L, Smith T. An epidemiologic model of severe morbidity and mortality caused by Plasmodium falciparum. Am J Trop Med Hyg. 2006;75:63–73.
Smith T, Ross A, Maire N, Rogier C, Trape JF, Molineaux L. An epidemiologic model of the incidence of acute illness in Plasmodium falciparum malaria. Am J Trop Med Hyg. 2006;75:56–62.
Gething PW, Patil AP, Smith DL, Guerra CA, Elyazar IR, Johnston GL, Tatem AJ, Hay SI. A new world malaria map: Plasmodium falciparum endemicity in 2010. Malar J. 2011;10:378.
Penny MA, Maire N, Bever CA, Pemberton-Ross P, Briët OJT, Smith DL, Gething PW, Smith TA. Distributions of malaria exposure in endemic countries in Africa considering country levels of effective treatment. Malar J. 2015;14:384.
Center for International Earth Science Information Network (CIESIN) CU. Global Rural-Urban Mapping Project (GRUMP): Urban extents. New York: Palisades; 2004.
Open Malaria decay functions. https://github.com/SwissTPH/openmalaria/wiki/ModelDecayFunctions-configuration.
Griffin JT, Hollingsworth TD, Okell LC, Churcher TS, White M, Hinsley W, Bousema T, Drakeley CJ, Ferguson NM, Basanez MG, Ghani AC. Reducing Plasmodium falciparum malaria transmission in Africa: a model-based evaluation of intervention strategies. PLoS Med. 2010;7:e1000324.
Bailey NJT. The biomathematics of malaria. London: Charles Griffin and Co Ltd; 1982.
Walker PG, White MT, Griffin JT, Reynolds A, Ferguson NM, Ghani AC. Malaria morbidity and mortality in Ebola-affected countries caused by decreased health-care capacity, and the potential effect of mitigation strategies: a modelling analysis. Lancet Infect Dis. 2015;15:825–32.
Eckhoff PA. Malaria parasite diversity and transmission intensity affect development of parasitological immunity in a mathematical model. Malar J. 2012;11:10–1186.
Maire N, Aponte JJ, Ross A, Thompson R, Alonso P, Utzinger J, Tanner M, Smith T. Modeling a field trial of the RTS,S/AS02A malaria vaccine. Am J Trop Med Hyg. 2006;75:104–10.
Wenger EA, Eckhoff PA. A mathematical model of the impact of present and future malaria vaccines. Malar J. 2013;12:10–1186.
Ballou WR. The development of the RTS,S malaria vaccine candidate: challenges and lessons. Parasite Immunol. 2009;31:492–500.
White MT, Verity R, Griffin JT, Asante KP, Owusu-Agyei S, Greenwood B, Drakeley C, Gesase S, Lusingu J, Ansong D, et al. Immunogenicity of the RTS,S/AS01 malaria vaccine over time and implications for duration of vaccine efficacy: analysis of data from a phase 3 randomised controlled trial. Lancet Infect Dis. 2015. doi:10.1016/S1473-3099(15)00239-X (Epub ahead of print).
Olotu A, Fegan G, Wambua J, Nyangweso G, Awuondo KO, Leach A, Lievens M, Leboulleux D, Njuguna P, Peshu N, et al. Four-year efficacy of RTS,S/AS01E and its interaction with malaria exposure. N Engl J Med. 2013;368:1111–20.
Penny MA, Maire N, Studer A, Schapira A, Smith TA. What should vaccine developers ask? Simulation of the effectiveness of malaria vaccines. PLoS One. 2008;3:e3193.
White MT, Griffin JT, Akpogheneta O, Conway DJ, Koram KA, Riley EM, Ghani AC. Dynamics of the antibody response to Plasmodium falciparum infection in African children. J Infect Dis. 2014;210:1115–22.
Crowell V, Yukich JO, Briet JT, Ross A, Smith TA. A novel approach for measuring the burden of uncomplicated Plasmodium falciparum malaria: application to data from Zambia. PLoS One. 2013:e57297.
Authors’ contributions
MAP designed the experiments, ran simulations, preformed the analysis and analysed results. PPR ran simulations. MAP drafted the manuscript. MAP and TAS conceived of the study. All authors read and approved the final manuscript.
Acknowledgements
The authors would like to thank Diggory Hardy for help with running simulations. Calculations were performed at sciCORE (http://scicore.unibas.ch/) scientific computing core facility at University of Basel. A large number of volunteers are gratefully thanked for making their computers available via http://www.malariacontrol.net for the simulations. We thank Peter Gething at the University of Oxford for providing estimates of parasite prevalence.
This work was funded by Bill & Melinda Gates Foundation (#OPP1032350) and PATH-Malaria Vaccine Initiative (MVI). No funding bodies had any role in the study design, data analysis, decision to publish, or preparation of the manuscript. Clinical trial data was previously published by RTS,S Clinical Trials Partnership [2], but this group did not fund the investigators to undertake the analysis.
Competing interests
The authors declare that they have no competing interests. The analysis for this study was conducted following a call initiated and facilitated by PATH-Malaria Vaccine Initiative and WHO. Employees of PATH-Malaria Vaccine Initiative and GSK reviewed and commented on early draft manuscripts, but were not involved in the final approval of the manuscript or final results.
Author information
Authors and Affiliations
Corresponding author
Additional file
12936_2015_969_MOESM1_ESM.pdf
Additional file 1: This file includes additional Figures of results that support and expand some of the results in the main text, but whose inclusion would detract from the main argument.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Penny, M.A., Pemberton-Ross, P. & Smith, T.A. The time-course of protection of the RTS,S vaccine against malaria infections and clinical disease. Malar J 14, 437 (2015). https://doi.org/10.1186/s12936-015-0969-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12936-015-0969-8