Abstract
Background
Common complex traits may involve multiple genetic and environmental factors and their interactions. Many methods have been proposed to identify these interaction effects, among them several machine learning and data mining methods. These are attractive for identifying interactions because they do not rely on specific genetic model assumptions. To handle the computational burden arising from an exhaustive search, including all possible combinations of factors, filter methods try to select promising factors in advance.
Methods
Model-based multifactor dimensionality reduction (MB-MDR), a semiparametric machine learning method allowing adjustment for confounding variables and lower level effects, is applied to Genetic Analysis Workshop 19 (GAW19) data to identify interaction effects on different traits. Several filtering methods based on the nearest neighbor algorithm are assessed in terms of compatibility with MB-MDR.
Results
Single nucleotide polymorphism (SNP) rs859400 shows a significant interaction effect (corrected p value <0.05) with age on systolic blood pressure (SBP). We identified 23 SNP–SNP interaction effects on hypertension status (HS), 42 interaction effects on SBP, and 26 interaction effects on diastolic blood pressure (DBP). Several of these SNPs are in strong linkage disequilibrium (LD). Three of the interaction effects on HS are identified in filtered subsets.
Conclusions
The considered filtering methods seem not to be appropriate to use with MB-MDR. LD pruning is further quality control to be incorporated, which can reduce the combinatorial burden by removing redundant SNPs.
Similar content being viewed by others
Background
Common complex traits, such as blood pressure, are at least partly based on complex molecular mechanisms likely to involve multiple genetic factors and their interactions. In addition, the extent to which genetic factors are expressed may also depend on interactions with environmental factors, such as age or sex. Factors influencing the trait of interest by nonlinear interaction with other factors may have a small effect on their own, and most traditional methods suffer from the curse of dimensionality as a consequence of small sample sizes.
As a result, several methods have been specifically proposed to identify gene–gene (G × G) and gene-environment (G × E) interactions. Two main classes of methods can be identified: parametric methods, like regression-based approaches, and nonparametric methods, which covers most machine learning and data-mining approaches. One widely used nonparametric method is the multifactor dimensionality reduction (MDR) [1] that has been extended and altered subsequently. Model-based MDR (MB-MDR) [2] is one alteration that bridges the aforementioned classes by combining advantages of nonparametric approaches, that is, no distributional assumptions are imposed, with those of parametric approaches, that is, adjustment for confounding variables and lower level main effects.
To handle the combinatorial challenge of millions to billions of possible factor combinations, filter algorithms have been proposed that select interesting factors in a preprocessing manner.
These approaches are combined in this study in application on Genetic Analysis Workshop 19 (GAW19) data to detect interactions and assess the usability of filter methods.
Methods
Data
Data provided by the GAW19 are used [3]. As real phenotype data, we use age, sex, systolic blood pressure (SBP), diastolic blood pressure (DBP), and antihypertensive medication (BPMEDS). We use high-quality hard genotype calls and restrict our analyses to biallelic variants, resulting in 163,622 single-nucleotide polymorphisms (SNPs). Hypertension status (HS) is defined by SBP >140 mmHg and DBP >90 mmHg or BPMEDS usage, yielding 219 cases and 1632 controls. Because of missing phenotype data, 92 samples were excluded.
Quality control
For quality control, we use a stepwise routine. In every step, samples with a call rate of less than 97 % or deviation from mean heterozygosity of more than three SD are excluded. Likewise, SNPs with a call rate of less than 98 % are excluded, separately for cases and controls, minor allele frequency (MAF) less than 1 %, or a p value of less than 0.00001 in a test for deviation from Hardy-Weinberg equilibrium (HWE) in controls. Steps are repeated until no more samples or SNPs are excluded. On the remaining data set principal components are analyzed to find genetic outliers. To find genetic relatives, SNPs are analyzed with R package [4] SNPRelate [5], and identity-by-descent (IBD) and identity-by-state (IBS) estimates are used to determine samples to remove.
Filtering of single-nucleotide polymorphisms
Filter methods can be applied to reduce the set of possible SNP combinations, thus reducing the computational burden in interaction analyses. These methods aim to select potentially important SNPs for subsequent analyses. We used nearest-neighbor-based filtering methods, namely Relief [6], ReliefF [7], Tuned ReliefF (TuRF) [8], Spatially Uniform ReliefF (SURF) [9], SURF* [10], multiSURF (multiple runs of SURF), and SURF*nTuRF (combination of SURF* and TuRF). Basically, all these filtering methods assign a weight to each SNP based on whether the nearest neighbor(s) of the same affection status and the nearest neighbor(s) of the other affection status group have the same or different genotypes. For further information on these methods, we refer you to the literature. All filtering methods are implemented in the MDR software package (ver. 3.0.2, http://sourceforge.net/projects/mdr/).
We apply all filtering methods to the quality-controlled data to select the 1000 top-weighted SNPs, using HS as affection status. All other parameters are set to default. For continuous traits such as DBP and SBP, these filtering methods are not applicable.
Model-based multifactor dimensionality reduction
MB-MDR [2] aggregates SNP combinations into risk groups with strong evidence regarding high or low risk of disease. Thus, the high-dimensional space of SNP combinations is reduced to a new 1-dimensional factor to increase the power to detect interactions. Applied to the analysis of SNP-SNP interactions in the Genetic Analysis Workshop (GAW) data the steps of MB-MDR are as follows:
-
Step 1:
Dimensionality reduction.
-
1.
Select two SNPs with three possible discrete genotypes each.
-
2.
Represent combination of selected SNPs in 2-dimensional space as cells c j , eg, 0–0, 0–1,…
-
3.
For j = 1,…,9, evaluate significance of association test T j on c j versus all other cells. The appropriate test depends on the trait. For HS a χ 2-test is used; for DBP and SBP a t-test is used.
-
If T j is not significant, label c j as O (“no evidence”);
-
Else if T j > 0, label c j as H(igh) risk;
-
Else label c j as L(ow) risk.
-
-
1.
-
Step 2:
Association test on lower-dimensional construct.
-
1.
Perform association test T H , comparing H versus {L, O}. Again, selection of association test depends on the trait (see Step 1).
-
2.
Perform association test T L , comparing L versus {H, O}. Again, selection of association test depends on the trait (see Step 1).
-
3.
Select max(T H , T L ).
-
1.
-
Step 3:
Significance assessment.
-
1.
Repeat Steps 1 and 2 for each possible SNP combination.
-
2.
Assess significance of each max(T H , T L ) by permutation-based maxT multiple-testing correction algorithm [11].
-
1.
The extension of the algorithm to higher-order interactions is straightforward. Furthermore, one SNP can be replaced by any environmental factor (age, sex) with discrete states to analyze G × E interactions. It should be noted that the term “model-based” in MB-MDR alludes to the use of statistical tests in Steps 1 and 2. For our analyses, we use the C++ implementation of MB-MDR (ver. 4.1.0, http://www.statgen.ulg.ac.be/software.html); for further information on this method, we refer the reader to the literature.
Genome-wide analysis of main effects
To assess the main effects of SNPs on HS, SBP, and DBP, MB-MDR is used with default settings but switched off interaction. We use a maximum of 100,000,000 permutations and the MAXT option for multiple-testing correction to obtain p values. Thus, p values are corrected for multiple testing within each of the analyses on HS, SBP, and DBP only. For computational feasibility, after each 100,000 permutations, the upper bound of a 95 % confidence interval, around 1.5 times the inverse of all permutations so far, is calculated. SNPs with an estimated p value exceeding this bound are removed from further permutation runs.
Model-based multifactor dimensionality reduction analyses for gene-environment interactions
We next analyze the interaction effects of all SNPs, using sex and age as environmental factors on HS, SBP, and DBP. Age is categorized into three balanced groups (young, middle, old). For adjustment for main effects, we use the co-dominant method of MB-MDR as suggested by Mahachie John et al [12]. We use 10,000 permutations and the speedMAXT option for multiple-testing correction to obtain p values. Again, p values are corrected for multiple testing within each of the analyses on HS, SBP, and DBP only. We compare these interaction results with the results from the main effect analyses to ensure that main effects do not drive interaction results.
Model-based multifactor dimensionality reduction analyses for SNP–SNP interactions
SNP–SNP interaction analyses on HS, SBP, and DBP are performed on the full set of SNPs, as well as on the top 1000 filtered SNPs on HS. If the filters work adequately for MB-MDR, we expect an overlap of identified interactions. We use a maximum of 10,000 permutations and speedMAXT option for multiple-testing correction to obtain p values. As before, p values are corrected for multiple testing within each of the analyses on HS, SBP, and DBP only.
Results
In nine runs of quality control, 33 samples were excluded because of deviation from mean heterozygosity. In addition, one sample was excluded after IBD analyses. A total of 1,586,958 SNPs were excluded because of low MAF and 1806 SNPs were excluded because of deviation from HWE in controls. After quality control, 1820 samples (216 cases, 1604 controls) and 46,746 SNPs remained.
Table 1 shows the results of screening for main effects. We identified one SNP with a significant interaction effect with age on SBP. As an example for the internal representation of factor combinations in MB-MDR we refer to Fig. 1, which shows the interaction rs859400 × age on SBP. We see a nonlinear interaction effect, as the risk for a higher SBP at every age depends on a different genotype at rs859400.
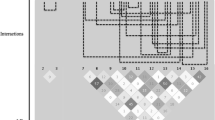
Figure 2 shows the results of SNP–SNP interaction analyses on the full set of SNPs. We identified 23 SNP–SNP interactions on HS, 42 interactions on SBP, and 26 interactions on DBP. There are no intersecting interaction effects between traits. Two clusters can be identified for SBP, one involving SNPs on chromosomes 1 and 19 (11 SNP–SNP interaction effects; 6 and 2 SNPs on chromosomes 1 and 19, respectively), another smaller cluster with SNPs on chromosomes 3 and 15 (7 SNP–SNP interaction effects; 3 and 6 SNPs on chromosomes 3 and 15, respectively). SNPs rs4802566 and rs4802565 on chromosome 19 in the first cluster are in strong linkage disequilibrium (LD) (r 2 = 0.9164), as well as several other SNPs on the other chromosomes in both clusters.
Pairwise SNP–SNP interactions. SNP–SNP interactions with p value <0.05 on unfiltered set, grouped by trait (HS, hypertension status; SBP, systolic blood pressure; DBP, diastolic blood pressure). Multiple SNP–SNP interactions on same chromosomes are stacked, p values are color-coded and corrected for multiple testing within the analyses on HS, SBP, and DBP. Annotations denote interaction effects that were identified in unfiltered and filtered subsets
Three interaction effects identified on the full set of SNPs are also contained in the filtered sets of SNPs: 1 by SURF, 2 by multiSURF. None of the other filtered sets of SNPs contain SNP pairs showing a p value of <0.05 in the full set of SNPs.
Discussion
We successfully identified nonlinear G × G and G × E interaction effects with MB-MDR. None of the identified main effects triggered an interaction effect. Clearly, these interaction effects need replication to rule out false-positive findings. For this, it might be of interest to compare our results to those of other GAW19 participants. The filtering methods considered did not select SNPs that are involved in the top interaction effects from the unfiltered set. A possible explanation is that the applied filter methods tend to select SNPs with a strong main effect. In contrast, MB-MDR is designed to identify nonlinear interactions, which may or may not have main effects as well.
Conclusions
Filters based on a nearest-neighbor approach are not suitable for analyses with the MB-MDR method. Based on the full set of SNP data, several SNPs in strong LD are identified involved in interaction effects. Although this is to be expected, this shows that LD pruning is a further quality control to be incorporated as it can reduce the combinatorial burden by removing surrogate SNPs.
References
Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, Parl FF, Moore JH. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet. 2001;69(1):138–47.
Calle ML, Urrea V, Vellalta G, Malats N, Steen KV. Improving strategies for detecting genetic patterns of disease susceptibility in association studies. Stat Med. 2008;27(30):6532–46.
Blangero J, Teslovich TM, Sim X, Almeida MA, Jun G, Dyer TD, Johnson M, Peralta JM, Manning AK, Wood AR, et al. Omics squared: human genomic, transcriptomic, and phenotypic data for Genetic Analysis Workshop 19. BMC Proc. 2015;9 Suppl 8:S2.
R Core Team: R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2014. https://www.R-project.org/.
Zheng X, Levine D, Shen J, Gogarten S, Laurie C, Weir B. A high-performance computing toolset for relatedness and principal component analysis of SNP data. Bioinformatics 2012;28(24):3326–28.
Kira K, Rendell LA. A practical approach to feature selection. In: Sleeman DH, Edwards P, editors. Proceedings of the Ninth International Workshop on Machine Learning (Aberdeen, Scotland, UK, 1–3 of July 1992). San Francisco: Morgan Kaufmann Publishers; 1992.
Kononenko I. Estimating attributes: analysis and extensions of RELIEF. In: Bergadano F, De Raedt L, editors. Machine Learning: ECML-94. Berlin: Springer; 1994. p. 171–82.
Moore JH, White BC. Tuning ReliefF for genome-wide genetic analysis. In: Marchiori E, Moore JH, Jagath C, Rajapakse JC, editors. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Berlin: Springer; 2007. p. 166–75.
Greene CS, Penrod NM, Kiralis J, Moore JH. Spatially Uniform ReliefF (SURF) for computationally-efficient filtering of gene–gene interactions. BioData Min. 2009;2(1):1–9.
Greene C, Himmelstein D, Kiralis J, Moore J. The informative extremes: using both nearest and farthest individuals can improve relief algorithms in the domain of human genetics. In: Pizzuti C, Ritchie M, Giacobini M, editors. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Berlin: Springer; 2010. p. 182–93.
Westfall PH, Young SS. Resampling-based Multiple Testing: Examples and Methods for p-Value Adjustment. New York: Wiley; 1993.
Mahachie John JM, Cattaert T, Lishout FV, Gusareva ES, Steen KV. Lower-order effects adjustment in quantitative traits model-based multifactor dimensionality reduction. PLoS One. 2012;7(1):e29594.
Acknowledgements
IRK was supported by the German Federal Ministry of Education and Research (BMBF, grant # 01ZX1313J).
Declarations
This article has been published as part of BMC Proceedings Volume 10 Supplement 7, 2016: Genetic Analysis Workshop 19: Sequence, Blood Pressure and Expression Data. Summary articles. The full contents of the supplement are available online at http://bmcproc.biomedcentral.com/articles/supplements/volume-10-supplement-7. Publication of the proceedings of Genetic Analysis Workshop 19 was supported by National Institutes of Health grant R01 GM031575.
Authors’ contributions
IRK designed the overall study and DG conducted statistical analyses and drafted the manuscript. Both authors read and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Gola, D., König, I.R. Identification of interactions using model-based multifactor dimensionality reduction. BMC Proc 10 (Suppl 7), 33 (2016). https://doi.org/10.1186/s12919-016-0019-8
Published:
DOI: https://doi.org/10.1186/s12919-016-0019-8