Background

Causal inference is a key task in epidemiology which discovers the causality between exposure and outcome. Theoretically, causality is the difference in outcome caused by a change in exposure, which can be gotten by ‘do-calculus’ in observational studies [1]. In practice, however, as exposure is impossible to intervene in analytic epidemiology, confounders inevitably distort the causal effect of exposure on outcome [2,3,4,5]. For majority of epidemiologists, adjusting for confounders using logistic regression model for dichotomous outcomes is the routine method [6,7,8,9,10]. Although some studies have verified that different adjustment strategies in logistic regression models might lead to different magnitudes of bias (the difference of the estimation minus the true causal effect) and precision [8, 11], it is still the most commonly used strategy in analytic epidemiologic studies. This phenomenon is mainly attributed to their vague knowledge about the behaviour of logistic regression model. For causal inference in observational study, the inverse probability weighting based marginal structural model (IPW-based-MSM) has been confirmed as an unbiased causal effect estimation approach to adjust for measured confounders [12,13,14]. Unfortunately, the advantages of IPW-based-MSM are not recognized by most epidemiologists. Furthermore, for both logistic regression and IPW-based-MSM, the selection of adjustment variables sets remains a big challenge. Fortunately, the concept of confounding equivalence (c-equivalence) proposed by Judea Pearl might help us to select adjusting strategies [15].

The c-equivalence is presented to determine whether two variables sets are equally valuable for adjustment, namely, whether adjustment for one set is guaranteed to have the same asymptotic bias as adjustment for the others [15]. Tests for c-equivalence are fairly easy to perform through a necessary and sufficient condition [15, 16], and they can also be implemented by propensity score methods [17]. This provides us a strategy for selecting adjusting variables sets when using logistic regression models and IPW-based-MSMs, which help to clarify whether adjusting for different c-equivalent sets has same bias-reducing potential.

In this paper, we focused on 4 typical causal diagrams (Fig. 1), which summarized the generalization of c-equivalence to detect the performances of logistic regression models and IPW-based-MSMs under the framework of c-equivalence. Both theoretical proofs and simulation studies were performed to determine whether adjusting for the sets of c-equivalence had the same bias-reducing potential and observed their precision in logistic regression models and IPW-based-MSMs respectively, and further comparing the performances of c-equivalence between these two models through assessing their accuracy (bias) and precision (standard error). Our aim was to highlight the problems of c-equivalence using logistic regression model as well as the advantages of IPW-based-MSM.

Fig. 1
figure 1

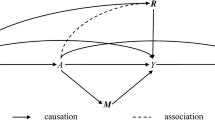
Four typical causal diagrams with various confounding paths from simple to complex for the target causal path X→Y. a contains only one confounding path (X←Z→T→Y). b contains two confounding paths (X←Z→T→Y, X←W→Y). Two confounding paths (X←Z→T→Y, X←W→V→Y) that have another node (V) are included in (c). d has three confounding paths (X←W→Y, X←Z→W→Y and X←W←T→Y). X and Y indicates exposure and outcome respectively. T, Z, W and V are all confounders that can be observed. {c 0, c 1, c 2, c 3, c 4, c 5} are the effect parameters. For example, the effect of Z on T is c 0

Full size image

Methods

C-equivalence and its test

Let X, Y and Z be three disjoint subsets of discrete variables, and P(x, y, z) are their joint distribution. The causal effect of X on Y can be defined as \( P\left(y| do(x)\right)=\sum \limits_zP\left(y|x,z\right)p(z) \) [5, 18, 19], where a sufficient set Z is chosen to include variables judged as “confounders” [16, 20, 21]. In this framework, the two confounders sets T and Z are c-equivalent if \( \sum \limits_tP\left(y|x,t\right)P(t)=\sum \limits_zP\left(y|x,z\right)P(z) \) ∀x, y. This means that adjustment for set T or Z would produce the same asymptotic bias relative to the target causal effect quantity [15]. To meet the necessary and sufficient condition of c-equivalence, it is first necessary to define the G-admissibility of a variables set S, which satisfies the back-door criterion [19]: 1) No element of S is a descendant of X; 2) The elements of S block every path between X and Y that contains an arrow into X. Another condition of c-equivalence is the identical Markov boundary [15], which is defined as: let S m be the minimal subset of S that satisfies the condition (X ⊥ S| S m ) G . This means that measurement of S m renders X independent of all other members of S, and no proper subset of S m has this property. Therefore, the necessary and sufficient conditions for T and Z to be c-equivalent are that at least one of the following conditions hold: 1) T m = Z m; and 2) T and Z are G-admissible [15].

As an example, Fig. 1 illustrates the four typical causal diagrams with simple and complex confounding paths for the target causal path X→Y [22]. For instance, Fig. 1d contains three confounding paths X←W→Y, X←Z→W→Y and X←W←T→Y, with three corresponding confounders Z, W and T [22, 23]. Theoretically, conditioning on {Z, W}, {T, W} or {Z, T, W} can achieve the same bias-reducing potential [23]. Thus, they are c-equivalent.

Statistical methods for adjusting for confounders

Expect for the well-known logistic regression model which is the habitual method for most of epidemiologists, IPW-based-MSM is an alternative approach that can obtain the unbiased causal effect estimation [24, 25]. In IPW-based-MSM, the unbiased causal effect is estimated by inverse probability weighted which can correct for confounding bias [26]. In this paper, the following stabilized weights, which has been recommended to increase the statistical efficiency and to achieve better coverage of the confidence intervals, were used [13, 27],

$$ {sw}_i=\frac{P\left(X={x}_i\right)}{P\left(X={x}_i|{Z}_i={z}_i\right)} $$

where Z is a set of variables which are considered to be confounders. By weighting the original observations using the stabilized weights (sw i ), we can fit the following marginal structural model to estimate the causal effect of X on Y,

$$ \mathrm{logit}\kern0.1em P\left({Y}_x=1\right)={\beta}_0^{MSM}+{\beta}_1^{MSM}x $$

where the causal effect estimation of X on Y is \( {\beta}_1^{MSM} \).

Theoretical derivation for bias-reducing potential of c-equivalence under logistic regression model

Taking Fig. 1a as an example, we deduced whether adjusting for different c-equivalence sets had the same bias-reducing potential under logistic regression by the following procedure.

1) Based on the necessary and sufficient condition, A 1 = {Z}, A 2 = {T} and A 3 = {Z, T} satisfied G-admissibility, thus they were equivalent, as denoted by A 1 ≈ A 2 ≈ A 3.

2) Calculated the true causal effect (ACE log(OR)) of X on Y through the average causal effect (ACE) on the scale of the logarithm odds ratio (OR),

$$ {ACE}^{\log (OR)}=\mathrm{logit}\left(P\left(Y=1| do\left(X=1\right)\right)\right)-\mathrm{logit}\left(P\left(Y=1| do\left(X=0\right)\right)\right) $$

3) Calculated the effect (\( {\beta}_X^{set} \)) of X on Y by logistic regression,

$$ {\displaystyle \begin{array}{l}{\beta}_X^{A_1}=\mathrm{logit}\left(P\left(Y=1|X=1,{A}_1\right)\right)-\mathrm{logit}\left(P\left(Y=1|X=0,{A}_1\right)\right)\\ {}{\beta}_X^{A_2}=\mathrm{logit}\left(P\left(Y=1|X=1,{A}_2\right)\right)-\mathrm{logit}\left(P\left(Y=1|X=0,{A}_2\right)\right)\\ {}{\beta}_X^{A_3}=\mathrm{logit}\left(P\left(Y=1|X=1,{A}_3\right)\right)-\mathrm{logit}\left(P\left(Y=1|X=0,{A}_3\right)\right)\end{array}} $$

4) Calculated the biases\( {\beta}_X^{A_1}-{ACE}^{\log (OR)} \), \( {\beta}_X^{A_2}-{ACE}^{\log (OR)} \) and \( {\beta}_X^{A_3}-{ACE}^{\log (OR)} \), and then deduced whether \( {\beta}_X^{A_1}-{ACE}^{\log (OR)}={\beta}_X^{A_2}-{ACE}^{\log (OR)}={\beta}_X^{A_3}-{ACE}^{\log (OR)} \).

Simulation

Taking the four typical causal diagrams, which covered the generalization of c-equivalence (Fig. 1), as examples, a series of simulation studies were performed to determine whether adjusting for the sets of c-equivalence had the same bias-reducing potential and observed their precision in logistic regression models and IPW-based-MSMs respectively, further compared the performances of c-equivalence between these two models though assessing their accuracy and precision.

Four simulation scenarios were considered, and assumed that: 1) all variables were binary and followed a Bernoulli distributions; and 2) the effects of parent nodes on their child nodes were positive and log-linearly additive. Logistic regression models were used to simulate child nodes from their corresponding parent nodes.

For scenario 1 (Fig. 1a), the simulated data were generated as follows. LetP(Z = 1) = π. Then, P(T = 1| Z) = exp(c 0 Z + α 1)/(1 + exp(c 0 Z + α 1)) was used to derive the probability of child node T from its parent node Z. Similarly, P(X = 1| Z) = exp(c 1 Z + α 2)/(1 + exp(c 1 Z + α 2)) and P(Y = 1| X, T) = exp(c 3 X + c 2 T + α 0)/(1 + exp(c 3 X + c 2 T + α 0)) were used to obtain the probability of X = 1 and Y = 1, respectively, where the parameters α 0, α 1, α 2 denoted the intercepts of Y, T and X, respectively, and each effect parameter (c 0, c 1, c 2, c 3) referred to the effect of the parent node on its corresponding child node. Simulated data was generated for 1000 subjects by above procedure.

In this scenario (Fig. 1a), variable sets A 1 = {Z}, A 2 = {T} and A 3 = {Z, T} satisfied the necessary and sufficient conditions of c-equivalence; thus, A 1 ≈ A 2 ≈ A 3. Therefore, we compared three adjustment strategies with the following six models,

model 1: \( \mathrm{logit}\left(p\left(Y=1|X,{A}_1\right)\right)={{\widehat{\beta}}^{A_1}}_0+{\widehat{\beta}}_X^{A_1}X+{{\widehat{\beta}}^{A_1}}_Z\mathrm{Z} \).

model 2: \( \mathrm{logit}\left(p\left(Y=1|X,{A}_2\right)\right)={{\widehat{\beta}}^{A_2}}_0+{\widehat{\beta}}_X^{A_2}X+{{\widehat{\beta}}^{A_2}}_TT \).

model 3: \( \mathrm{logit}\left(p\left(Y=1|X,{A}_3\right)\right)={{\widehat{\beta}}^{A_3}}_0+{\widehat{\beta}}_X^{A_3}X+{{\widehat{\beta}}^{A_3}}_TT+{{\widehat{\beta}}^{A_3}}_ZZ \).

model 4: \( \mathrm{logit}\kern0.1em P\left({Y}_x^{A_1}=1\right)={\widehat{\beta}}_0^{MSM\_{A}_1}+{\widehat{\beta}}_x^{MSM\_{A}_1}x \) \( {sw}_i^{A_1}=\frac{P\left(X={x}_i\right)}{P\left(X={x}_i|{A}_{1i}={A}_{1i}\right)} \).

model 5: \( \mathrm{logit}\kern0.1em P\left({Y}_x^{A_2}=1\right)={\widehat{\beta}}_0^{MSM\_{A}_2}+{\widehat{\beta}}_x^{MSM\_{A}_2}x \) \( {sw}_i^{A_2}=\frac{P\left(X={x}_i\right)}{P\left(X={x}_i|{A}_{2i}={A}_{2i}\right)} \).

model 6: \( \mathrm{logit}\kern0.1em P\left({Y}_x^{A_3}=1\right)={\widehat{\beta}}_0^{MSM\_{A}_3}+{\widehat{\beta}}_x^{MSM\_{A}_3}x \) \( {sw}_i^{A_3}=\frac{P\left(X={x}_i\right)}{P\left(X={x}_i|{A}_{3i}={A}_{3i}\right)} \).

where\( {\widehat{\beta}}_X^{A_1} \), \( {\widehat{\beta}}_X^{A_2} \), \( {\widehat{\beta}}_X^{A_3} \), \( {\widehat{\beta}}_X^{MSM\_{A}_1} \), \( {\widehat{\beta}}_X^{MSM\_{A}_2} \) and \( {\widehat{\beta}}_X^{MSM\_{A}_3} \) denoted the causal effect estimations after conditioning on A 1 , A 2 and A 3 by logistic regression and IPW-based-MSM, respectively. Given the true causal effect \( A\widehat{C}{E}^{\log (OR)} \) calculated by do-calculus, both the biases (\( {\widehat{\beta}}_X^{A_1}-A\widehat{C}{E}^{\log (OR)} \),\( {\widehat{\beta}}_X^{A_2}-A\widehat{C}{E}^{\log (OR)} \), \( {\widehat{\beta}}_X^{A_3}-A\widehat{C}{E}^{\log (OR)} \), \( {\widehat{\beta}}_x^{MSM\_{A}_1}-A\widehat{C}{E}^{\log (OR)} \), \( {\widehat{\beta}}_x^{MSM\_{A}_2}-A\widehat{C}{E}^{\log (OR)} \), \( {\widehat{\beta}}_x^{MSM\_{A}_3}-A\widehat{C}{E}^{\log (OR)} \)) and their corresponding standard errors (\( \mathrm{SE}\left({\widehat{\beta}}_X^{A_1}\right) \), \( \mathrm{SE}\left({\widehat{\beta}}_X^{A_2}\right) \), \( \mathrm{SE}\left({\widehat{\beta}}_X^{A_3}\right) \), \( \mathrm{SE}\left({\widehat{\beta}}_X^{MSM\_{A}_1}\right) \), \( \mathrm{SE}\left({\widehat{\beta}}_X^{MSM\_{A}_2}\right) \) and \( \mathrm{SE}\left({\widehat{\beta}}_X^{MSM\_{A}_3}\right) \)) were used to identify whether adjusting for different c-equivalence sets A 1, A 2 or A 3 still produced the same bias-reducing under the logistic regression model and IPW-based-MSM, further to evaluate their accuracy and precision.

For scenario 2 (Fig. 1b), similar simulation data sets were created as scenario 1. In this scenario, A 1 = {Z, W}, A 2 = {T, W} and A 3 = {Z, T, W} satisfied G-admissibility; thus, A 1 ≈ A 2 ≈ A 3. Therefore, three corresponding logistic regression models and three corresponding IPW-based-MSMs conditional on A 1 , A 2 or A 3 were constructed to identify whether the c-equivalence has identical biases and to evaluate their precisions. In addition, B 1 = {Z} was c-equivalent to B 2 = {Z, T}, namely, B 1 ≈ B 2, due to their identical Markov boundary, written as B 1m = B 2m = {Z}. Therefore, four corresponding models conditioning on B 1 or B 2 were used to calculate the biases and standard errors.

In scenario 3 (Fig. 1c), the simulated data was generated in the same way as in scenario 1. In addition, the sets A 1 = {Z} ≈ A 2  = {Z, T} and B 1 = {W} ≈ B 2 = {W,V} were separately c-equivalent due to A 1m = A 2m = {Z} and B 1m = B 2m = {W}. As A 1 ≈ A 2 and B 1 ≈ B 2 were identical in the c-equivalence mechanism, it was sufficient to analyze one group to explore the c-equivalence mechanism of the identical Markov boundary. Thus, we constructed two logistic regression models and two IPW-based-MSMs conditioning on A 1 or A 2 to explore their c-equivalence and to evaluate their precision. Furthermore, as variables sets C 1 = {Z,W}, C 2 = {T,V} and C 3 = {Z,W,T,V} blocked all back-door paths from X to Y, they were admissible and equivalent, C 1 ≈ C 2 ≈ C 3. Therefore, the six corresponding models conditional on C 1, C 2 or C 3 were performed to identify biases and precisions.

For scenario 4 (Fig. 1d), following the path directions, simulation data sets were created same with scenario 1. A 1 = {Z, W}, A 2 = {T, W} and A 3 = {Z, T, W} satisfied G-admissibility; thus, A 1 ≈ A 2 ≈ A 3. Their corresponding three logistic regression models and three IPW-based-MSMs conditional on A 1 , A 2 or A 3 were used to observe the biases and precisions.

For each of the 4 simulation scenarios, we varied across the effect of a specific edge given the others fixed with 1000 simulation repetitions. The R (http://cran.r-project.org/) programming language was used to conduct the statistical simulations.

Results

Theoretical results for bias-reducing potential of c-equivalence under logistic regression model

Considered scenario 1 (Fig. 1a) as a typical diagram for deducing whether adjusting for different c-equivalence sets resulted in the same bias reduction under the logistic regression models. In this causal diagram, A 1 = {Z}, A 2 = {T} and A 3 = {Z, T} composed the c-equivalence group, which satisfied the G-admissibility .

For A 1 ≈ A 2 ≈ A 3 of c-equivalence, the true causal effect of X on Y was calculated as

$$ {\displaystyle \begin{array}{l}{ACE}^{\log (OR)}=\mathrm{logit}\left[P\Big(Y=1| do\left(X=1\right)\Big)\right]-\mathrm{logit}\left[P\Big(Y=1| do\left(X=0\right)\Big)\right]\\ {}{ACE}^{\log (OR)}=\mathrm{logit}\kern.2em \left[\sum \limits_{Z,T}P\left(Y=1|X=1,T\right)P\Big(T|Z\Big)P(Z)-\mathrm{logit}\left[\sum \limits_{Z,T}P\left(Y=1|X=0,T\right)P\Big(T|Z\Big)P(Z)\right.\right]\end{array}} $$

By conditioning on A 1 = {Z}, the effect of X on Y was equal to

$$ {\displaystyle \begin{array}{l}{\beta}_{\mathrm{X}}^{A_1}=\mathrm{logit}\left[P\left(Y=1|X=1,Z\right)\right]-\mathrm{logit}\left[P\left(Y=1|X=0,Z\right)\right]\\ {}\kern1.7em =\mathrm{logit}\left[\sum \limits_TP\left(Y=1|X=1,T\right)P\left(T|Z\right)\right]-\mathrm{logit}\left[\sum \limits_TP\left(Y=1|X=0,T\right)P\left(T|Z\right)\right]\end{array}} $$

Similarly, the effect of X on Y when conditioning on A 2 = {T} was equal to

$$ {\displaystyle \begin{array}{l}{\beta}_{\mathrm{X}}^{A_2}=\mathrm{logit}\left[P\left(Y=1|X=1,T\right)\right]-\mathrm{logit}\left[P\left(Y=1|X=0,T\right)\right]\\ {}\kern1.6em =\mathrm{logit}\left[P\left(Y=1|X=1,T\right)\sum \limits_TP\left(T|Z\right)\right]-\mathrm{logit}\left[P\left(Y=1|X=0,T\right)\sum \limits_TP\left(T|Z\right)\right]\end{array}} $$

Additionally, the effect of X on Y when conditioning on A 3 = {T, Z} was equal to

$$ {\displaystyle \begin{array}{l}{\beta}_{\mathrm{X}}^{A_3}=\mathrm{logit}\left[P\left(Y=1|X=1,T,Z\right)\right]-\mathrm{logit}\left[P\left(Y=1|X=0,T,Z\right)\right]\\ {}\kern1.8em =\mathrm{logit}\left[P\left(Y=1|X=1,T\right)\right]-\mathrm{logit}\left[P\left(Y=1|X=0,T\right)\right]\end{array}} $$

After a series of derivations (Additional file 1: Appendix), we obtained \( {\beta}_X^{A_2}={\beta}_X^{A_3} \) under any condition, suggesting that the bias-reducing after adjusting for c-equivalence sets A 2  ≈ A 3 was equivalent under the logistic regression model. \( {\beta}_X^{A_1}={\beta}_X^{A_2}={\beta}_X^{A_3} \) only if c 2 = 0  or c 3 = 0, indicating that the bias-reducing after adjusting for c-equivalence sets A 1 ≈ A 2  ≈ A 3, respectively, was equivalent in this situation. However, \( {\beta}_X^{A_1}<{\beta}_X^{A_2}={\beta}_X^{A_3} \) if c 2 ≠ 0 and c 3 > 0, and \( {\beta}_X^{A_1}>{\beta}_X^{A_2}={\beta}_X^{A_3} \) if c 2 ≠ 0 and c 3 < 0,which indicating an unequal bias-reducing after adjusting for c-equivalence sets A 1 ≈ A 2  ≈ A 3 when both c 2 and c 3 were not equal to zero (for more details, see Appendix).

Simulation results

Scenario 1

For Fig. 1a, various simulation strategies were performed. From the panel a and panel b of Fig. 2 and Additional file 2: Figure S1, as for the logistic regression models, we observed that adjusting for the c-equivalent set A 2 or A 3 has resulted in approximate biases, but adjusting for set A 1 was not equal to them. Moreover, the strategy of adjusting for A 1 achieved the minimum bias. When adjusting for confounders by IPW-based-MSM, the estimations of all the strategies were approximate and unbiased. Panel c and d of Fig. 2 and Additional file 2: Figure S1 showed that adjusting for A 2 by IPW-based-MSM achieved the highest precision in all situations. Thus, compared with logistic regression models, the IPW-based-MSM produced an unbiased causal effect estimation and the highest precision in this scenario. The optimal adjustment strategy was conditioning on A 2. Although the estimations through logistic regression model were biased, adjusting for A 1 produced a result nearest to the true causal effect.

Fig. 2
figure 2

Scenario 1 (Fig. 1a), simulation results of the bias (a and b) and standard error (c) and (d) of c-equivalence sets A 1 ≈ A 2 ≈ A 3 when varied across the log transformed odds ratio effect of Z on T and T on Y

Full size image

When varying across the effect of Z on T with the other parameters fixed, the simulation results indicated that the biases of all six models (models 1–6) tended to be stable (Fig. 2a). Similar performances were observed when varying across the effect of Z on X (Additional file 2: Figure S1a). However, when varying across the effect of T on Y and keeping the other parameters constant, the bias showed a linear increasing trend after adjusting for set A 2 or A 3 under the logistic regression model, but was approximately to zero after adjusting for set A 1. However, the biases remained stable under IPW-based-MSM (Fig. 2b). We observed similar trends with the effect of X on Y increasing (Additional file 2: Figure S1b).

Scenario 2

In Fig. 1b, for the first c-equivalent subsets A 1 = {Z, W}, A 2 = {T, W} and A 3 = {Z, T, W}, we observed that the bias after adjusting for set A 2 was similar to that of A 3 but not to that of A 1, and the strategy of adjusting for A 1 achieved the minimum bias under the logistic regression models, as shown in panels a and b of Fig. 3, Additional file 3: Figure S2 and Additional file 4: Figure S3 under logistic regression models. The adjustment of any confounding sets of c-equivalent subsets through IPW-based-MSM had the same bias-reducing potential and the estimations were unbiased. Panel c and d of these figures showed that adjusting for A 2 under IPW-based-MSM achieved the highest precision in all situations. Thus, conditioning on any c-equivalent set that was satisfied G-admissibility through IPW-based-MSM produced an unbiased causal effect estimate and adjustment for A 2 was the best strategy. When using logistic regression models to adjust for confounders, the optimal adjustment strategy was adjusting for variable subset A 1.

Fig. 3
figure 3

Scenario 2 (Fig. 1b), simulation results of the bias (a and b) and standard error (c and d) of c-equivalence sets A 1 ≈ A 2 ≈ A 3 when varied across the log transformed odds ratio effect of T on Y and W on Y

Full size image

In the logistic regression models, when keeping the other parameters constant, bias elevated with the effect of T on Y increasing when adjusting for A 2 or A 3, whereas it elevated in the opposite direction when adjusting for A 1 (Fig. 3a). All three models revealed increased biases with the effects of W on Y increasing (Fig. 3b). Similar performances were observed when varying across the effect X on Y (Additional file 3: Figure S2b). When varying across the effect of Z on T with the other parameters fixed, the simulation results indicated that the biases of all three adjustment strategies tended to be stable (Additional file 3: Figure S2b). We observed similar trends with the increase of the effect of Z on X (Additional file 4: Figure S3a) or the effect of W on X (Additional file 4: Figure S3b). When adjusting for confounders through IPW-based-MSM, the biases of all three adjustment strategies tended to be stable in all situations.

For another c-equivalent subsets B 1 = {Z} and B 2 = {Z, T}, panels a and b of Fig. 4, Additional file 5: Figure S4 and Additional file 6: Figure S5 showed that adjusting for c-equivalence set B 1 or B 2 had different bias-reducing, and the bias of adjusting for B 1 was less than that of adjusting for B 2 under the logistic regression models. For IPW-based-MSM, the biases were equivalent after adjusting for B 1 or B 2. Panels c and d of these figures showed that adjusting for B 2 through IPW-based-MSM resulted in higher precision.

Fig. 4
figure 4

Scenario 2 (Fig. 1b), simulation results of the bias (a and b) and standard error (c and d) of c-equivalence sets B 1 ≈ B 2 when varied across the log transformed odds ratio effect of T on Y and W on Y

Full size image

Keeping the other parameters constant, the bias elevated as the effect of T on Y increasing when adjusting for set B 2, whereas it was stable after adjusting for B 1 under logistic regression. A stable trend also appeared after adjusting for any sets through IPW-based-MSM (Fig. 4a). Similar performances were observed when varying across the effect of X on Y (Additional file 5: Figure S4b). When varying across the effect of W on Y with the other parameters fixed, the simulation results indicated that biases of four models revealed an increasing trend (Fig. 4b). Similar trends of the effect of W on X increasing were observed in Additional file 6: Figure S5b. When varying across the effect of Z on T with the other parameters fixed, the biases of the four models were stable (Additional file 5: Figure S4a). Similar performances were observed when varying across the effect of Z on X (Additional file 6: Figure S5a).

Scenario 3

In Fig. 1c, for the first c-equivalent subsets, A 1 = {Z} and A 2  = {Z, T}, Fig. 5, Additional file 7: Figure S6 and Additional file 8: Figure S7 showed that adjusting for c-equivalence set A 1 or A 2 resulted in different bias-reducing, and the bias of adjusting for A 1 was less than that after adjusting for A 2 under logistic regression models. Then the biases were equal after conditioning on A 1 and A 2 via IPW-based-MSM. In consideration of the standard error, adjusting for A 2 through IPW-based-MSM resulted in higher precision.

Fig. 5
figure 5

Scenario 3 (Fig. 1c), simulation results of the bias (a and b) and standard error (c and d) of c-equivalence sets A 1 ≈ A 2 when varied across the log transformed odds ratio effect of Z on T and V on Y

Full size image

For other c-equivalent subsets C 1 = {Z,W}, C 2 = {T,V} and C 3 = {Z,W,T,V}, the simulation result (Fig. 6, Additional file 9: Figure S8 and Additional file 10: Figure S9) showed that adjusting for the variable set C 2 resulted in similar bias to that of set C 3 but not to C 1, and the strategy of adjusting for C 1 resulted in the minimum bias under the logistic regression models. However, the estimations of all strategies conditioned by IPW-based-MSM were approximately equivalent and unbiased. For the standard error, conditioning on C 2 by IPW-based-MSM resulted in the minimum standard error in all situations. Thus, IPW-based-MSM was a better method than logistic regression for controlling for confounders. The optimal adjustment strategy was conditioning on C 2 by IPW-based-MSM in this scenario. Besides, adjusting for A 1 produced the result that was nearest to the true causal effect under the logistic regression model.

Fig. 6
figure 6

Scenario 3 (Fig. 1c), simulation results of the bias (a and b) and standard error (c and d) of c-equivalence sets C 1 ≈ C 2 ≈ C 3when varied across the log transformed odds ratio effect of Z on T and V on Y

Full size image

Scenario 4

For Fig. 1d, simulation results (Fig. 7, Additional file 11: Figure S10 and Additional file 12: Figure S11) showed that adjusting for c-equivalence set A 2 or A 3 had different bias-reducing but adjusting for A 1 was not equal to them and the strategy of adjusting for A 1 got the minimum bias than others under logistic regression models. Conditioning on any confounding set through MSM had the same bias-reducing and produce unbiased estimations. In consideration of the standard error, we observed that adjusting for A 2 by IPW-based-MSM resulted in higher precision in all situations. Thus, IPW-based-MSM produced unbiased causal effect estimations after conditioning on any c-equivalent set, and the strategy of adjusting for A 2 achieved highest precision in this scenario. When using logistic regression models to adjust for confounders, adjusting for variables subset A 1 produced the minimum bias.

Fig. 7
figure 7

Scenario 4 (Fig. 1d), simulation results of the bias (a and b) and standard error (c and d) of c-equivalence sets A 1 ≈ A 2 ≈ A 3when varied across the log transformed odds ratio effect of W on X and T on Y

Full size image

Discussion

In this paper, we focused on the 4 typical causal diagrams shown in Fig. 1 to assess the performances of logistic regression models and IPW-based-MSMs with respect to c-equivalence. The necessary and sufficient conditions for T and Z to be c-equivalent proposed by Pearl are that at least one of the following conditions hold [15]: 1) T m = Z m; or 2) T and Z are G-admissible. Our results revealed that c-equivalence sets satisfying the c-equivalence condition 1) (e.g., A 2 (T) and A 3 (Z, T) in scenario 2) had different bias-reducing under logistic regression. For c-equivalence condition 2), adjusting for the set including all confounders had approximately bias-reducing as adjusting for the set containing the parent nodes of Y, while adjusting for the set containing the parent nodes of X was not equivalent to adjusting for the two above sets. However, under the framework of IPW-based-MSM, conditioning on any set of c-equivalence, as judged by the necessary and sufficient conditions, still had same bias-reducing. In summary, adjusting for different sets of c-equivalence under logistic regression always produced different bias-reducing; whereas when using IPW-based-MSM, the estimations of all strategies were approximately equivalent.

Adjusting more confounders would improve accuracy and precision of estimation in classic linear regression [28, 29]. Nevertheless, including more confounders in logistic regression model usually leads to less bias and lower precision [30]. Our studies showed that adjusting for the set containing the parent nodes of X had the minimum bias in logistic regression. With regard to the standard error, adjusting for set with fewer confounders would improve precision. Under the framework of IPW-based-MSM, we observed that adjusting for any set satisfying condition 2) had unbiased estimations; and conditioning on the set containing all parent nodes of Y achieved the highest precision in all situations. In summary, compared with logistic regression, the IPW-based-MSM produced unbiased causal effect estimates when the adjusted variable sets satisfied condition 2) and the optimal adjustment strategy was conditioning on parent nodes of outcome Y, which achieved the highest precision. Although the estimations obtained by logistic regression was biased, the estimation of adjusting for the parent nodes of the exposure X was nearest to true causal effect.

The true causal effect of exposure on outcome calculated by “do-calculus” is defined in terms of marginal probability distributions. However, the conditional treatment effects estimated from logistic regression model differ from the true causal effect [31, 32]. Logistic regression estimates do not behave like linear regression estimates. They are affected by omitted variables, even when those variables are unrelated to the independent variables in the model [11]. The use of IPW-based-MSM could lead to a more precise estimation of causal effects.

The discrepancy between the marginal OR and the conditional OR even in the absence of confounders is acknowledged as the non-collapsibility of the OR [4, 33]. The non-collapsibility effect depends on a variety of parameters, e.g., the effect of the exposure, the prevalence and effect of the covariate [4, 33]. According to our results, the differences in estimates between the logistic regression model and IPW-based-MSM were equal to the non-collapsibility effect in number. However, the discrepancy in estimates between these two model were different after adjusting for different sets of c-equivalence maybe due to these sets have different variables.

Conclusions

In conclusion, the bias-reducing differed after adjusting for the sets of c-equivalence under the logistic regression model, whereas it were approximately equivalent when using IPW-based-MSM. All adjustment strategies through logistic regression were biased, while IPW-based-MSM could always obtain unbiased estimation when the adjusted set satisfied G-admissibility. Thus, for adjusting confounders set, we recommend IPW-based-MSM rather than logistic regression model.