Abstract
Background
The microstructure of trabecular bone is a composite trait governed by a complex interaction of multiple genetic determinants. Identifying these genetic factors should significantly improve our ability to predict of osteoporosis and its associated risks. Genetic mapping using collaborative cross mice (CC), a genetically diverse recombinant inbred mouse reference panel, offers a powerful tool to identify causal loci at a resolution under one mega base-pairs, with a relatively small cohort size.
Here, we utilized 31 CC lines (160 mice of both sexes in total) to perform genome-wide haplotype mapping across 77,808 single-nucleotide polymorphisms (SNPs). Haplotype scans were refined by imputation with the catalogue of sequence variation segregating in the CC to suggest potential candidate genes. Trabecular traits were obtained following microtomographic analysis, performed on 10-μm resolution scans of the femoral distal metaphysis. We measured the trabecular bone volume fraction (BV/TV), number (Tb.N), thickness (Tb.Th), and connectivity density (Conn.D).
Results
Heritability of these traits ranged from 0.6 to 0.7. In addition there was a significant (P < 0.01) sex effect in all traits except Tb.Th. Our haplotype scans yielded six quantitative trait loci (QTL) at 1 % false discovery rate; BV/TV and Tb.Th produced two proximal loci each, on chromosome 2 and 7, respectively, and Tb.N and Conn.D yielded one locus on chromosomes 8 and 14, respectively. We identified candidate genes with previously-reported functions in bone biology, and implicated unexpected genes whose function in bone biology has yet to be assigned. Based on the literature, among the genes that ranked particularly high in our analyses (P < 10-6) and which have a validated causal role in skeletal biology, are Avp, Oxt, B2m (associated with BV/TV), Cnot7 (with Tb.N), Pcsk6, Rgma (with Tb.Th), Rb1, and Cpb2 (with Conn.D). Other candidate genes strongly suggested by our analyses are Sgcz, Fgf20 (associated with Tb.N), and Chd2 (with Tb.Th).
Conclusion
We have demonstrated for the first time genome-wide significant association between several genetic loci and trabecular microstructural parameters for genes with previously reported experimental observations, as well as proposing a role for new candidate genes with no previously characterized skeletal function.
Similar content being viewed by others
Background
Osteoporosis is the most common bone disease, affecting nearly half the US population over the age of 50 years, and is expected to cost over $25.3 billion by 2025 [1] per-annum. Worldwide, the incidence of bone fractures is expected to increase by 2.7-fold by 2050, due to population aging [2]. Importantly, women have a 1.5-fold higher risk of bone fracture than men throughout their lives as well as a 1.3-fold higher risk of hip or vertebral fracture than their risk of breast cancer [3–5]. A number of studies have shown that peak bone mass is tightly affected by host genetic determinants, and low bone mass significantly increases the risk of osteoporosis, especially in the elderly [6]. Risk of fracture is determined largely by the combination of bone structural parameters associated with bone strength. Most of these parameters, e.g. trabecular bone density, achieve peak values at skeletal maturity and subsequently decrease due to aging and menopause [6]. Microstructural features of trabecular bones, as those of cortical bones and indeed of most phenotypes, are known to be complex rather than Mendelian traits, determined by the cumulative effects and interactions of numerous genetic loci and environmental factors [7, 8].
Individuals with the same bone mineral density (BMD) measured by two dimensional dual energy x-ray absorptiometry (DXA) scans have different risks for fracture, suggesting that factors other than density, such as microstructural architecture, are important determinants of skeletal strength [9]. Recently, a number of genome-wide association studies (GWAS), including a meta-analysis, described >50 loci associated with bone mineral density (BMD) in humans [10–15]. However, many candidate genes, such as vasopressin (Avp), oxytocin (Oxt), and β-2-microglobulin (B2m) were not confirmed by GWAS, despite their proven role in bone metabolism [12, 13, 15–18]. Failure to significantly associate these genes to bone density in GWAS suggests that there may be other bone phenotypes not yet studied [17], or that genetic variation segregating in the populations tested does not influence the expression of these genes appreciably.
Importantly, almost all previous GWAS have used areal bone mineral density (aBMD) as the sole parameter for the bone phenotype. Clinically, areal and volumetric BMD (aBMD and vBMD) do not accurately predict risk fracture, suggesting that site-specific changes at the microstructural level are important determinants of bone strength. BMD as measured by DXA is a two dimensional projection that cannot determine or account for bone size, individual bone compartment shape (trabecular vs cortical), or the underlying microstructure. Notably, fracture risk and bone strength are tightly associated with changes in the bone microstructure, but are not always detected by DXA and peripheral computed tomography (pQCT) [19]. There is growing evidence that cortical and trabecular bone have distinct genetic influences and should be analyzed separately [15, 16]. Indeed, a recent GWAS in collaborative cross (CC) mice, based on DXA measurements, failed to reveal any heritability of BMD [20], whereas our preliminary analyses in the same mouse panel (some of these data are as yet unpublished, others are reported herein) show highly significant heritability levels in most of the microstructural parameters measured by micro-computed tomography (μCT).
The CC is a panel of recombinant inbred lines of mice descended from eight genetically divergent strains [21], designed for high resolution analysis of complex traits, with particular emphasis on traits relevant to human health [22, 23]. In this study we used 31 CC lines which at the time of the experiment were over 90 % homozygous. GWAS in mice traditionally use rodent inbred line crosses with poor mapping resolution of 20 to 40 Mb [24], thus proposing hundreds of genes as potential candidates. To narrow the widths of QTLs, combined cross-analysis and block haplotyping techniques have been proposed [24, 25]. Mapping resolution in the CC is typically of the order of 1–2 Mb, due to the increased extent of observable recombination in the population and the use of haplotype-based tests of association [18, 22–25]. Genetic variation segregating in the CC is much greater (over 30 million SNPs, due to the inclusion of three wild-derived strains) than in a traditional intercross between standard laboratory strains (about 4 million SNPs) [7]. In addition to the narrower QTLs typically generated using the CC panels, this allows the identification of a greater number of contributing genetic variants as compared to panels based on classical strains only. Moreover, by using the extensive catalogues of variation in the founders (see Keane et al., 2011 [7]) it is possible to impute the variants into each CC lines and test for association [26]. By merging the CC founders according to the strain distribution pattern (SDP) of their alleles at potential quantitative trait nucleotides (QTN) within a given QTL (obtained by the initial haplotype-based mapping) [26, 27], one can refine the initial haplotype mapping and identify candidate genes.
Here, we aimed to identify new genetic determinants of bone microarchitecture and metabolism associated with bone strength in CC mice. In contrast to working with human populations in which the environment is uncontrolled and individuals are genetically distinct, in the CC we could collect phenotypes in a controlled environment and from multiple individuals with the same genetic background. We measured microarchitectural trabecular bone traits, including trabecular bone volume fraction (BV/TV), trabecular bone number (Tb.N), trabecular bone thickness (Tb.Th), and trabecular bone connectivity (Conn.D) in the distal femoral metaphysis. Our results provide the first genome-wide confirmation of the involvement of several genetic factors in trabecular bone development as well as suggest new candidate genes with undocumented roles in bone metabolism.
Results
Trabecular traits vary across the CC population
In each CC animal we analyzed the trabecular bone compartment of the distal femoral metaphysis and measured trabecular bone volume fraction (BV/TV; range = 2.38 – 29.2 %), trabecular number (Tb.N; range = 0.63 – 5.64 mm-1), trabecular thickness (Tb.Th; range = 35.95 – 60.0 μm), and trabecular connectivity (Conn.D; range = 14.0 – 205.09 mm-3). Heritability (H2) for all traits was greater than 0.6, i.e., genetic differences between the lines explained most of the phenotypic variation (Table 1). There was a high phenotypic heterogeneity between lines for all traits except for Tb.Th. While phenotypic heterogeneity was observed in both males and females, female variability among the lines was greater (Additional file 1: Figure S1).
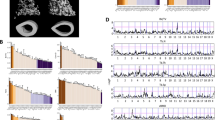
Figure 1 shows the phenotypic distribution across lines, sorted in descending order by their mean. Lines are color-coded according to Duncan’s least significance range (LSR). This partitioned the lines to at least three groups of lines in which each group significantly differs from the others (P < 0.001). Additional file 2: Table S1 lists the means of the lines for each trait. To emphasize the phenotype variations across the lines, we identified the two lines with extreme values for BV/TV, Tb.N, and Conn.D (Figs. 1 and 2). Interestingly, in all traits except Tb.Th, IL-1513 was at the upper-most extreme and IL-2126 and IL-2391 (and in BV/TV also IL-557) were at the lower-most extreme (Figs. 1 and 2).
Mean trabecular values obtained from 31 CC lines. From top-left, counter-clockwise: trabecular bone volume fraction (BV/TV; %), trabecular number (Tb.N; mm-1), thickness (Tb.Th; mm), and connectivity density (Conn.D; mm-3). Lines were grouped according to Duncan’s LSR; each color-coded group is statistically different from all the other groups (P < 0.001; Tukey’s ANOVA-based test for multiple comparisons). Bars are Mean + SE
Our analyses showed that all phenotypes were approximately normally distributed and positively correlated with one another (Additional file 2: Table S2). Pearson’s correlation coefficient (r) ranged between 0.93 for BV/TV vs. Tb.N, and 0.29 for BV/TV vs. Tb.Th. However, despite these overall high phenotypic correlations, some lines were discordant between the bone traits. For example, IL-670 had high trabecular Conn.D (88.82 mm-3) but average Tb.N and BV/TV (2.42 mm-1 and 8.8 %), and low Tb.Th (45.73 μm). IL-557 was in the lower range for BV/TV, Tb.N and Conn.D (5.3 %, 1.42 mm-1 and 47.86 mm-3) but was average for Tb.Th (47.43 μm).
Because body weight is often correlated with bone density [28, 29], we assessed the effect of weight on our examined traits. Irrespective of sex effects, our data indicate that body weight did not affect any of the analyzed bone parameters in this animal sample (Pearson’s r ≤ 0.11). In contrast, sex had a significant impact on BV/TV, Tb.N, and Conn.D (P < 0.001), but not on Tb.Th (Table 1, Fig. 3). Notably, males always averaged higher for the three traits where we observed a sex effect (Fig. 3 and Additional file 1: Figure S1). Although age was in the limited range of 10–13 weeks, we did observe a significant age effect for BV/TV (P < 0.001, Table 1).
Sex effects on trabecular traits. Notched box-and-whisker plots demonstrating the interquartile range (IQR; median in bold, whiskers correspond to ± 1.5 · IQR) for BV/TV (%), Tb.N (mm-1), Tb.Th (mm), and Conn.D (mm-3). Significance is reported in logP values (a negative log-transform of the P-value, to emphasize the extent to which they differ). Note that except for Tb.Th, all traits had a significant sex effect (P < 0.01, or logP > 2)
Mapping the albino trait supports a modest number of CC lines
As a positive control, we performed a QTL mapping for albinism using the same mice from 31 CC lines in which we measured the bone traits, and in an additional 7 lines in which no skeletal analysis was performed (38 lines in all). Using the same methodology, we were able to map albinism to its known locus on chromosome 7 [30]. This confirms that the identities of the phenotyped lines matched their expected genotypes and provides validation for using a small number of CC lines for QTL mapping (Additional file 3: Figure S2).
Haplotype association mapping reveals six QTLs
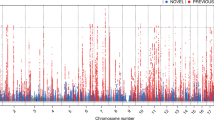
After adjusting for sex and age and taking the mean for each line, we performed a haplotype association analysis (Fig. 4). Using the full database for each trait, we obtained haplotype mappings which were correlated in a manner that echoed the phenotype correlation; this practice has limitations in that it can mask important loci. In other words, the complex nature of the trabecular traits is prone to loss of information owing to presumed complementary genetic factors that govern each trait. This phenomenon dilutes the sample and adds noise which accumulates false negatives. QTL masking can also be due to genetic drift occurring in inbred population of high generation [31, 32]. To overcome this hindrance we sampled subsets from our cohort and unlocked otherwise confounded loci (this was achieved with a minimum of 28 lines); here, therefore, each trait is founded on the set that maximizes its loci mapping’s peaks. For BV/TV and Tb.Th, we found two proximal QTLs for each on chromosome 2 and 7, respectively. Tb.N and Conn.D yielded one QTL on chromosome 8 and another on chromosome 14, respectively. The two QTLs for BV/TV, the QTL for Tb.N, the two QTLs for Tb.Th, and the QTL for Conn.D, are hereafter referred as trabecular-related loci (Trl) 1 to 6, respectively.
QTL haplotype mapping of trabecular traits. Plots show –logP values according to the chromosome location (x-axis). Horizontal line represent the 99th (solid) and 95th (dashed) percentile thresholds for genome-wide significance. a The scan for BV/TV yielded two proximal QTLs, at chromosome 2, with their peaks at a -logP of 6.67 and 6.31, respectively. b Tb.N had a QTL at chromosome 8 with a -logP of 5.63. c Tb.Th had two QTLs at chromosome 7 with a -logPs of 7.87 and 5.36. d Conn.D had a QTL at chromosome 14 with a -logP of 6.36
All QTLs are above the genome-wide 99th percentile threshold; they were obtained empirically by 200 permutation simulations, with an experiment-wide false discovery rate (FDR) under 1 % for each scan. As shown in Table 2 and Additional file 4: Figure S3, the respective widths of the 50 % confidence intervals (CIs) for Trl1 to 6 were 0.2, 0.3, 3.27, 0.2, 0.13, and 9.94 Mb. We also calculated 50 % CIs according to Li’s method (Table 2, [33]). The CIs obtained by our simulations were comparable to those calculated after Li, albeit the latter were usually slightly wider.
We then estimated the regional heritability (H2 r) explained by each QTL and found the combined values were approximately equal to the genome-wide H2. For the 6 defined Trl, the H2 r range fell between 0.60 and 0.86 (Table 2).
Subsequently, we assessed the haplotype contribution of the founder strains to each QTL (Fig. 5); Trl1, Trl2, Trl4, and Trl5 associated with BV/TV and Tb.Th, were predominantly affected by the PWK founder strain. In contrast, the loci associated with Tb.N and Conn.D (Trl3 and Trl5, respectively) had a more varied founder contribution.
Founder effects at each QTL. Each panel corresponds to one of the six mapped trabecular-related loci (Trl). The x-axis shows the eight founders of the CC population and the y-axis shows the haplotype effects predicted from a regression fit to the founder haplotype probabilities at the QTL. All effects are plotted relative to WSB which is arbitrarily set to 0. a Trl1 (BV/TV). b Trl2 (BV/TV). c Trl3 (Tb.N). d Trl4 (Tb.Th). e Trl5 (Tb.Th). f Trl6 (Conn.D)
Imputation identifies candidate genes
To pinpoint candidate genes we fine-tuned our model using merge analysis (Fig. 6, [26]) to test the association of variants imputed from the catalogue of variation in the eight CC founders. When the logP value of the imputation test is lower than that of the haplotype analysis, the SNPs at the QTL peak are unlikely to be causal; in contrast when the merge logP is higher, it suggests that the tested variant is consistent with being a quantitative trait nucleotide (QTN), with the caveat that there may be multiple variants with the same SDP that are equally likely to be causal [34]. Filtering out SNPs with logP values lower than that of the haplotype-scan peak SNPs we were able to identify candidate genes.
Merge analysis at each QTL. Each panel corresponds to one of the six mapped QTLs. The x-axis is the genome location; the left y-axis is the logP of the association test between the trait and the locus; and the right y-axis is the recombination rate scale, in 4Ner/Kb. The continuous black line is a section of the haplotype-based genome scans in Fig. 4. The red (MA; multiallelic) and gray (BA; biallelic) dots correspond to the results of the merge analyses. Genes appear in the legend as colored bars from top to bottom as their order of appearance in the image, from left to right. Dotted line is the 99th percentile threshold from Fig. 4. Blue continues line represents recombination rates. For clarity, merge logP values below 4 are not shown. a Trl1 (BV/TV). b Trl2 (BV/TV). c Trl3 (Tb.N). d Trl4 (Tb.Th). e Trl5 (Tb.Th). f Trl6 (Conn.D)
The list of all potential causal variants identified by the merge analysis is presented in Additional file 2: Table S3. In accordance with the relatively wide 50 % CI of Conn.D (Trl6), the peak of the haplotype analysis did not contain the highest merge logP values; rather, these lay within ±3 Mb from the inferred peak. Regarding Trl4 and Trl5 (Tb.Th), their 50 % CI is much narrower than that of Trl6 (0.2 and 0.13 vs 9.94 Mb, respectively, Table 2 and Additional file 4: Figure S3), but the peak of the QTL lacks a high density of SNPs with merge logP higher than the haplotype-scan logP threshold (Fig. 6). Moreover, those present are multiallelic, a situation which reflects the complexity observed in the predicted founders’ haplotype effects, and suggesting the presence of multiple causal variants (Fig. 6). To gain further insight into the Trls, we included recombination rates for the mouse at 4Ner/Kb, following Brunschwig et al. [35] (Fig. 6); although most loci are in regions of mild recombination rates, data for Trl3, 4, and 6 suggest that these loci are in the vicinity of recombination hot spots. We note that this did not alter the imputation performance (see Discussion).
We identified 11 potential genes for the six Trls; we found three genes for BV/TV (Trl1 and Trl2), three for Tb.N (Trl3), three for Tb.Th (Trl4 and Trl5), and two for Conn.D (Trl6). Importantly, our analysis revealed genes that already have well-documented functions in bone biology as well as genes that have yet an unexplored role in the regulation of trabecular bone microarchitecture (Additional file 2: Table S3).
Discussion
To our knowledge, this study is the first to use the CC population in a genome-wide association analysis of high-resolution trabecular bone traits. Our results replicate previous association analyses, confirm previous in vivo and in vitro experiments, and suggest new candidate genes for the regulation of trabecular bone microstructure. The roles of these latter genes will require validation in future studies both in vivo and in vitro. We thus provide a valuable resource for further research aimed at understanding the underlying genetic determinants of complex trabecular structure.
Our association analyses were enhanced by virtue of ancestral sequence information that enabled us to deduce QTNs that segregate differentially in the CC lines, thus reducing false positives and assisting in the identification of potential candidate genes. This imputation’s power depends on (a) the accuracy of the catalogues of variants in the CC founders (as determined from resequencing the strains by Keane et al. 2011 [7]) and (b) the accuracy with which the genome mosaics of the CC lines are determined from SNP genotypes using the HAPPY R package. Whilst we cannot control for sequencing errors in the founders, any uncertainty in the locations of mosaic breakpoints is encoded in the probability distribution of descent from each of the eight founders. At loci with high certainty (which are the great majority) the probability distribution is concentrated on one founder which has a much higher probability (close to 1) than that other strains (all close to 0). Around breakpoints the probability distribution transitions through a short region of uncertainty in which the strain probabilities are more equal. The way imputation (merge analysis) is performed in the CC is to compute the dosage of a SNP allele in a CC line by adding together the probabilities for those founders carrying that allele in the variant catalogue. This means that in regions of low certainty (where the founders are equally likely) the dosage of the allele will be approximately proportional to its frequency among the founders. In regions of high certainty the dosage is dominated by the founder strain with highest probability (i.e., the dosage will be close to 0 or 1). Genetic association with the SNP is determined by linear regression on the imputed dosages. The effect on association testing is that at a given SNP, the majority of CC lines will have high-confidence dosages close to 0 or 1, and a small minority (those with breakpoints near the SNP) will have intermediate dosages. These latter have relatively little impact on the statistical significance of the association, which is driven by the high-confidence lines.
We were able to narrow the interval to the kilo-base range by coinciding the CI with the 99th percentile threshold and imputation results for four out of six QTLs, namely, Trl1, Trl2 (for BV/TV), Trl4, and Trl5 (for Tb.Th), and thus to focus on a more restricted number of candidate genes.
Our findings indicate 4 Trls for which there was a strong founder effect by PWK. This emphasizes the advantage of the CC mouse panel, inasmuch as it includes 3 wild-derived strains, including the PWK strain. This strain differs from classical laboratory strains by about 17 million SNPs [7], and it is likely to carry rare variants not found in the classical inbred strains. This unique allelic diversity results in the presence of variants in more genes than in inbred populations, thus enabling the detection of a larger array of genes that contribute to the analyzed traits.
We detected 3 genes associated with BV/TV; two under Trl1 and one under Trl2. Among these, Oxt encodes a precursor of oxytocin, and Avp encodes arginine-vasopressin. Both of these proteins are hormones produced in the hypothalamus and secreted from the posterior pituitary gland, and differ from each other by only two amino acids. Tamma et al. have previously shown that these hormones have a direct skeletal effect – affecting BV/TV, Tb.N, and Tb.Th - in both males and females. They act via the hypothalamus-pituitary-skeletal axis [12, 13]. Oxt affects both osteoblasts and osteoclasts; it increases osteoblast differentiation by upregulating bone morphogenic protein (BMP) 2, and stimulates osteoclasts directly via activation of NF-kB and MAP kinase signaling, and indirectly via increasing RANK-L expression. Concordantly, Oxt-null mice exhibit an osteoporosis phenotype [12]. Avp deficiency, similarly, renders mice susceptible to bone loss via activation of the Avpr1a and Avpr2 G-protein coupled receptors, present in both osteoclasts and osteoblasts, which in turn activate the Erk pathway [13]. B2m encodes β2-microglobulin, which is involved in the regulation of the host immune response and is known to activate osteoclasts and osteoblasts in both sexes. It supports the transition of epithelial to mesenchymal cells, thereby promotes bone metastases originating from prostate, breast, lung, and renal cancers [18]. It does so mainly by interacting with hemochromatosis (HFE) protein. HFE null mice were found to be phenotypically identical to BMP2-null mice [36]. Further, men with a mutation in HFE had significantly lower BMD [37]. Interestingly, a recent study found that lysyl oxidase (LOX) plays a major role in the facilitation of bone metastases [38]; BMP1 proteolytically cleaves Pro-LOX to active LOX [39].
Under the QTL for Tb.N we identified Cnot7, Fgf20, and Sgcz to be the most prominent contributors to the phenotype. Cnot7 - or CCR4-NOT transcription complex, subunit 7 - suppresses bone mass and inhibits BMPs in osteoblasts [40]; Cnot7-null male mice had a substantial increase in bone mass, supposedly by inhibiting the expression of alkaline phosphatase induced by BMPs in osteoblastic cells. Fgf20 and Sgcz (fibroblast growth factor and ζ-sarcoglycan, respectively) have no documented role in bone metabolism. Fgf20 is a transcriptional target of β-catenin which is important during Wnt signaling [41] and interacts with BMP7 [42]. Wnt/β-catenin signaling is an established pathway for normal bone homeostasis [43]. Sgcz is expressed in both striated and smooth muscles. Importantly, bone and muscle share some common genes [44]. As of yet, it remains unclear whether these proteins affect both sexes equally and thus further work is needed to examine their differential expression in males and females.
For Tb.Th the strongest candidate genes were Pcsk6, Rgma, and Chd2. Pcsk6 encodes paired amino acid converting enzyme 4 (PACE4) which, in human females, evokes proteolytic degradation of aggrecan, a major cartilage molecule, by activating the proteases ADAMTS-4 and pro-ADAMTS-4, thereby inducing the development of osteoarthritis [45]. Interestingly, tibial trabecular bone structure was found to be a good predictor of knee osteoarthritis [46]. Rgma (encodes repulsive guidance molecule A) has been shown to be a co-receptor of BMP-2 and BMP-4, by binding directly to these factors, and to mediate their signaling via BMP type I and II receptors [36, 47, 48]. Based on the International Mouse Phenotyping Consortium database [49], both female and male mice with mutant Chd2 (encodes chromodomain helicase DNA binding protein 2) have a profoundly higher bone mineral content and greater bone area, although these findings have yet to be published in a peer-reviewed journal.
We speculate that putative skeletal role for genes associated with Conn.D can be assigned to Cpb2, Rb1, and Esd. Cpb2 (carboxypeptidase B2) has been implied to confer a protective role in the pathogenesis of osteoarthritis in male mice [50]. Rb1 was found to have a role in osteogenesis [51]. Again, further work is needed to determine if this role is sex-dependent.
Importantly, the peak of the QTL for Conn.D had almost no significant merge logP SNPs and the 50 % CI was large enough to speculate that genes therein are false positives; there reside Lrch1 (encodes Leucine-Rich Repeats And Calponin Homology (CH) Domain Containing 1) and Esd (encodes esterase D). Lrch1 was found in a previous GWAS exploring the knee osteoarthritis phenotype in humans [52], but large-scale replication studies [53, 54] then dismissed it from being casual. However, Esd was confirmed by microarray-based qPCR analysis to influence spinal bone mineral density in inbred rats [8] and thus seems to be a likely candidate. Still, due to insufficient evidence in our and previous studies, the role of these genes in bone microstructure remains unclear.
The genes aforementioned are most likely to explain the Trls, based on published functionality assays. However, it is possible that other genes in the vicinity of these loci are related to the traits examined. While these cannot be ruled out conclusively without carrying out particular validation experiments, they are unlikely to play a prominent role in determining the trabecular microstructure given their known molecular role. Of note, considering the meaningful sex and age effect some of the phenotypes exhibit, we expect some genes to have a sex and age differential behavior, even though none of the loci (and their human orthologues) were found on either of the sex chromosomes (Additional file 2: Table S3). Lastly, besides Avp and Oxt which are confirmed to affect the microstructural parameters we studied here, others have yet to be validated for these skeletal traits.
Conclusions
The variation of trabecular phenotypes between perfectly viable CC lines reflects in many aspects the variance in human populations. Whilst the complete complex spatial and temporal interactions of the genes controlling trabecular traits cannot be expected to be identified with a limited cohort size at our disposal, nevertheless, using a relatively small cohort with sufficient replication in each line, the wide phenotypic range of divergence enabled us to dissect the genetic architecture of trabecular phenotypes, and to direct previous genes associated with bone to more refined trabecular microstructural parameters.
Methods
Mice
Mice aged 10 to 13 weeks (male n = 86; female n = 74), from 31 different CC lines (average of 5 mice per line) were used in this study. The mice were at inbreeding generations of 11 to 37, which correspond to 80–99.9 % genetic homozygosity, respectively. The mice were bred and maintained at the small animal facility of the Sackler Faculty of Medicine, Tel Aviv University (TAU), Israel. They were housed on hardwood chip bedding in open-top cages, with food and distilled water available ad libitum, in an identical controlled environment (temperature = 25 ± 2 °C; 60 % ≤ humidity ≤ 85 %) and a 12 h light/dark cycle. All experiments protocols were approved by the Institutional Animal Care and Use Committee (IACUC M-13–014) at TAU, which follows the NIH/USA animal care and use protocols.
Specimen collection
Mice were intraperitoneally euthanized with cervical dislocation performed approximately one minute after breathing stops owing to 5 % Isoflurane inhalation. Left femora were harvested and fixed for 24 h in 4 % paraformaldehyde solution, and then stored in 70 % ethyl alcohol.
μCT evaluation
Whole left femora from each mouse were examined as described previously [55] by a μCT system (μCT 50, Scanco Medical AG, Switzerland). Briefly, scans were performed at a 10-μm resolution in all three spatial dimensions. The mineralized tissues were differentially segmented by a global thresholding procedure [56]. All morphometric parameters were determined by a direct 3D approach [57]. Parameters analyzed were determined in the metaphyseal trabecular bone, which included trabecular bone volume fraction (BV/TV), trabecular thickness (Tb.Th), trabecular number (Tb.N), and trabecular connectivity density (Conn.D).
Genotyping
A representative male mouse from each line was initially genotyped with a high mouse diversity array (MDA), which consists of 620,000 SNPs (Durrant et al., 2011). After about two intervals of 4 generations of inbreeding, all the CC lines were regenotyped by mouse universal genotype array (MUGA, 7,500 markers) and finally with the MegaMuga (77,800 markers) SNP array to confirm their genotype status [21]. The founder-based mosaic of each CC line was reconstructed using a hidden Markov model in which the hidden states are the founder haplotypes and the observed states are the CC lines, to produce a probability matrix of descent from each founder. This matrix was then pruned to about 11,000 SNPs by averaging across a window of 20 consecutive markers for faster analyses and reduction of genotyping errors [58].
Statistical analyses
All statistical analyses were performed with the statistical software R (R core development team 2009), including the package happy.hbrem [59].
Heritability and sex and age effects
Broad-sense heritability (H2) was obtained for each trait by fitting the trait (the independent variable) to the CC line label in a linear regression model that incorporates sex and age. ANOVA test was used to compare a null model (in which all dependent variables are set to 0) with linear models that fit the sex, age and the CC line labels to the examined trait. Practically, the difference between the residual sum of squares (RSS; \( {\displaystyle {\sum}_1^n{\left({\mu}_i - {\widehat{\mu}}_i\right)}^2} \)) of the covariates model and that of the CC-line labels can be seen as the net genetic contribution to the trait. Thus, this difference divided by that of the covariate model gives an estimation of the heritability. Sex and age effects were calculated separately, by dividing the RSS difference between the null and full model with that of the null model. Let F 0 be the model that fits the trait to the covariates; F 1 the model that fits the trait to the covariates and the CC line label; and F 00 the null model. Then, employing ANOVA, heritability is:
Similarly, sex and age effects are computed separately, by fitting separately each covariate in F 0. The covariate effect is thus:
Haplotype mapping
Each trait was fitted in a multiple linear regression model to the probability matrix of descent from each founder, including sex and age as covariates. The expected trait value from two ancestors, termed the genetic fit, is:
where μ is a normally distributed trait mean, with sex and age incorporated; F Li (s, t) is the probability of descent from founders s and t; and β s + β t is the additive effect of founders s and t. Because \( {\displaystyle {\sum}_s}{\displaystyle {\sum}_t}{F}_{Li}\left(s,t\right)=2 \) for a diploid organism, the maximum likelihood estimates \( {\widehat{\beta}}_s \) are not independent. Thus, they are expressed here as differences from the WSB/EiJ founder effect, so that \( {\widehat{\beta}}_{WSB}=0 \). Number of members per line was weighted and integrated in the linear model. ANOVA was then used to compare this model with a null model where the founder effects are all set to 0; the resulting F-statistic yielded the significance of the genetic model vs. the null model and the negative 10-base logarithms of the P values (logP) were recorded.
Permutations of the CC lines between the phenotypes were used to set significance thresholds levels. Founder effects are the estimates derived from the multiple linear regression fit above.
Regional heritability (Hr 2) was hereafter computed by ANOVA as in the broad-sense heritability computation, except that here null linear regression fit was compared with a genetic linear regression fit with the probability matrix of the founder descent at the peak QTL as the explanatory variable.
False discovery rate (FDR) was calculated using the p.adjust function in R, with the method “BH”.
Confidence intervals
Confidence intervals (CIs) were obtained both by simulations and by the quick method of Li, 2011 [33]. In the simulations, we resampled the residuals of the original linear regression fit at the peak of each QTL and rescanned 100 intervals within 7–10 Mb of the original loci to find the highest logP. Accordingly, following Durrant et al. [27], 1000 QTLs were simulated: if \( {\widehat{t}}_i \) is a random permutation of the residuals of fitted genetic model at the QTL peak, and K is a marker interval in a neighborhood of 3.5 to 5 Mb of the QTL peak L, a set of values for each trait, Z iK is provided by:
Merge analysis
In the merge analysis the eight founder strains are partitioned and merged according to the strain distribution pattern (SDP) of the alleles at the quantitative trait nucleotides (QTN) within a given QTL (formerly obtained by the initial mapping). If we denote the polymorphism as p, then X p = 1 if s has allele a at p, and X p = 0 otherwise [34]. Then, at p, the probability of i to inherit alleles a and b from s and t, respectively, within L is
This merges the founder strains by p. The expected trait value in the merged strains can now be inferred by
Because this is a sub-model of the QTL model, it is expected to yield higher logP values due to a reduction in the degrees of freedom. Significance was obtained by comparing the merge model with the QTL model. Individual genes were extracted from the Sanger mouse SNP repository (http://www.sanger.ac.uk/sanger/Mouse_SnpViewer).
Availability of supporting data
The data sets supporting the results of this article are available in the GitHub repository: https://github.com/roylv/avp.
Abbreviations
- BMD:
-
Bone mineral density
- BMP:
-
Bone morphogenic protein
- BV/TV:
-
Bone-volume fraction
- CC:
-
Collaborative cross
- CI:
-
Confidence interval
- Conn.D:
-
Trabecular connectivity density
- DXA:
-
X-ray absorptiometry (DXA)
- FDR:
-
False discovery rate
- GWAS:
-
Genome-wide association study
- H2 :
-
Heritability
- SDP:
-
Strain distribution pattern
- SNP:
-
Single nucleotide polymorphism
- LSR:
-
Least significant range
- TAU:
-
Tel Aviv University
- Tb.N:
-
Trabecular number
- Tb.Th:
-
Trabecular thickness
- Trl:
-
Trabecular-related loci
- μCT:
-
Micro computed tomography
- QTL:
-
Quantitative trait locus
- QTN:
-
Quantitative trait nucleotide
References
Burge R, Dawson-Hughes B, Solomon DH, Wong JB, King A, Tosteson A. Incidence and economic burden of osteoporosis-related fractures in the United States, 2005-2025. J Bone Miner Res. 2007;22:465–75.
Gullberg B, Johnell O, Kanis JA. World-wide projections for hip fracture. Osteoporos Int. 1997;7:407–13.
Garnero P, Sornay-Rendu E, Claustrat B, Delmas PD. Biochemical markers of bone turnover, endogenous hormones and the risk of fractures in postmenopausal women: the OFELY study. J Bone Miner Res. 2000;15:1526–36.
Sambrook P, Cooper C. Osteoporosis. Lancet. 2006;367:2010–8.
Van Staa TP, Dennison EM, Leufkens HG, Cooper C. Epidemiology of fractures in England and Wales. Bone. 2001;29:517–22.
Bab I, Hajbi-Yonissi C, Gabet Y, Müller R. Micro-Tomographic Atlas of the Mouse Skeleton. Boston, MA: Springer US; 2007.
Keane TM, Goodstadt L, Danecek P, White MA, Wong K, Yalcin B, et al. Mouse genomic variation and its effect on phenotypes and gene regulation. Nature. 2011;477:289–94.
Alam I, Sun Q, Koller DL, Liu L, Liu Y, Edenberg HJ, et al. Genes influencing spinal bone mineral density in inbred F344, LEW, COP, and DA rats. Funct Integr Genomics. 2010;10:63–72.
Chappard D, Baslé MF, Legrand E, Audran M. New laboratory tools in the assessment of bone quality. Osteoporos Int. 2011;22:2225–40.
Styrkarsdottir U, Halldorsson BV, Gretarsdottir S, Gudbjartsson DF, Walters GB, Ingvarsson T, et al. Multiple genetic loci for bone mineral density and fractures. N Engl J Med. 2008;358:2355–65.
Richards JB, Rivadeneira F, Inouye M, Pastinen TM, Soranzo N, Wilson SG, et al. Bone mineral density, osteoporosis, and osteoporotic fractures: a genome-wide association study. Lancet. 2008;371:1505–12.
Tamma R, Colaianni G, Zhu L, DiBenedetto A, Greco G, Montemurro G, et al. Oxytocin is an anabolic bone hormone. Proc Natl Acad Sci U S A. 2009;106:7149–54.
Tamma R, Sun L, Cuscito C, Lu P, Corcelli M, Li J, et al. Regulation of bone remodeling by vasopressin explains the bone loss in hyponatremia. Proc Natl Acad Sci U S A. 2013;110:18644–9.
Paternoster L, Lorentzon M, Lehtimäki T, Eriksson J, Kähönen M, Raitakari O, et al. Genetic determinants of trabecular and cortical volumetric bone mineral densities and bone microstructure. PLoS Genet. 2013;9:e1003247.
Estrada K, Styrkarsdottir U, Evangelou E, Hsu Y-H, Duncan EL, Ntzani EE, et al. Genome-wide meta-analysis identifies 56 bone mineral density loci and reveals 14 loci associated with risk of fracture. Nat Genet. 2012;44:491–501.
Paternoster L, Lorentzon M, Vandenput L, Karlsson MK, Ljunggren O, Kindmark A, et al. Genome-wide association meta-analysis of cortical bone mineral density unravels allelic heterogeneity at the RANKL locus and potential pleiotropic effects on bone. PLoS Genet. 2010;6:e1001217.
Hsu Y-H, Kiel DP. Clinical review: Genome-wide association studies of skeletal phenotypes: what we have learned and where we are headed. J Clin Endocrinol Metab. 2012;97:E1958–77.
Josson S, Nomura T, Lin J-T, Huang W-C, Wu D, Zhau HE, et al. β2-microglobulin induces epithelial to mesenchymal transition and confers cancer lethality and bone metastasis in human cancer cells. Cancer Res. 2011;71:2600–10.
Bagi CM, Hanson N, Andresen C, Pero R, Lariviere R, Turner CH, et al. The use of micro-CT to evaluate cortical bone geometry and strength in nude rats: correlation with mechanical testing, pQCT and DXA. Bone. 2006;38:136–44.
Iraqi FA, Athamni H, Dorman A, Salymah Y, Tomlinson I, Nashif A, et al. Heritability and coefficient of genetic variation analyses of phenotypic traits provide strong basis for high-resolution QTL mapping in the Collaborative Cross mouse genetic reference population. Mamm Genome. 2014;25:109–19.
Collaborative Cross Consortium. The genome architecture of the Collaborative Cross mouse genetic reference population. Genetics. 2012;190:389–401.
Threadgill DW, Hunter KW, Williams RW. Genetic dissection of complex and quantitative traits: from fantasy to reality via a community effort. Mamm Genome. 2002;13:175–8.
Churchill GA, Airey DC, Allayee H, Angel JM, Attie AD, Beatty J, et al. The Collaborative Cross, a community resource for the genetic analysis of complex traits. Nat Genet. 2004;36:1133–7.
Li R, Lyons MA, Wittenburg H, Paigen B, Churchill GA. Combining data from multiple inbred line crosses improves the power and resolution of quantitative trait loci mapping. Genetics. 2005;169:1699–709.
Wang X, Paigen B. Genetics of variation in HDL cholesterol in humans and mice. Circ Res. 2005;96:27–42.
Yalcin B, Flint J, Mott R. Using progenitor strain information to identify quantitative trait nucleotides in outbred mice. Genetics. 2005;171:673–81.
Durrant C, Tayem H, Yalcin B, Cleak J, Goodstadt L, de Villena FP-M, et al. Iraqi F a: Collaborative Cross mice and their power to map host susceptibility to Aspergillus fumigatus infection. Genome Res. 2011;21:1239–48.
Felson DT, Zhang Y, Hannan MT, Anderson JJ. Effects of weight and body mass index on bone mineral density in men and women: the Framingham study. J Bone Miner Res. 1993;8:567–73.
Anandacoomarasamy A, Caterson I, Sambrook P, Fransen M, March L. The impact of obesity on the musculoskeletal system. Int J Obes (Lond). 2008;32:211–22.
Ram R, Mehta M, Balmer L, Gatti DM, Morahan G. Rapid identification of major-effect genes using the collaborative cross. Genetics. 2014;198:75–86.
Deng H-W. Population Admixture May Appear to Mask, Change or Reverse Genetic Effects of Genes Underlying Complex Traits. Genetics. 2001;159:1319–23.
Valdar W, Flint J, Mott R. Simulating the collaborative cross: power of quantitative trait loci detection and mapping resolution in large sets of recombinant inbred strains of mice. Genetics. 2006;172:1783–97.
Li H. A quick method to calculate QTL confidence interval. J Genet. 2011;90:355–60.
Yalcin B, Fullerton J, Miller S, Keays DA, Brady S, Bhomra A, et al.Unexpected complexity in the haplotypes of commonly used inbred strains of laboratory mice. Proc Natl Acad Sci USA. 2004;101:9734–9.
Brunschwig H, Levi L, Ben-David E, Williams RW, Yakir B, Shifman S. Fine-Scale Maps of Recombination Rates and Hotspots in the Mouse Genome. Genetics. 2012;191:757–64.
Truksa J, Peng H, Lee P, Beutler E. Bone morphogenetic proteins 2, 4, and 9 stimulate murine hepcidin 1 expression independently of Hfe, transferrin receptor 2 (Tfr2), and IL-6. Proc Natl Acad Sci U S A. 2006;103:10289–93.
Guggenbuhl P, Deugnier Y, Boisdet JF, Rolland Y, Perdriger A, Pawlotsky Y, et al. Bone mineral density in men with genetic hemochromatosis and HFE gene mutation. Osteoporos Int. 2005;16:1809–14.
Cox TR, Rumney RMH, Schoof EM, Perryman L, Høye AM, Agrawal A, et al. The hypoxic cancer secretome induces pre-metastatic bone lesions through lysyl oxidase. Nature. 2015;522:106–10.
Maruhashi T, Kii I, Saito M, Kudo A. Interaction between periostin and BMP-1 promotes proteolytic activation of lysyl oxidase. J Biol Chem. 2010;285:13294–303.
Washio-Oikawa K, Nakamura T, Usui M, Yoneda M, Ezura Y, Ishikawa I, et al. Cnot7-null mice exhibit high bone mass phenotype and modulation of BMP actions. J Bone Miner Res. 2007;22:1217–23.
MacDonald BT, Tamai K, He X. Wnt/beta-catenin signaling: components, mechanisms, and diseases. Dev Cell. 2009;17:9–26.
Barak H, Huh S-H, Chen S, Jeanpierre C, Martinovic J, Parisot M, et al. FGF9 and FGF20 maintain the stemness of nephron progenitors in mice and man. Dev Cell. 2012;22:1191–207.
Kramer I, Halleux C, Keller H, Pegurri M, Gooi JH, Weber PB, et al. Osteocyte Wnt/beta-catenin signaling is required for normal bone homeostasis. Mol Cell Biol. 2010;30:3071–85.
Karasik D, Kiel DP. Genetics of the musculoskeletal system: a pleiotropic approach. J Bone Miner Res. 2008;23:788–802.
Malfait A-M, Seymour AB, Gao F, Tortorella MD, Le Graverand-Gastineau M-PH, Wood LS, et al. A role for PACE4 in osteoarthritis pain: evidence from human genetic association and null mutant phenotype. Ann Rheum Dis. 2012;71:1042–8.
Woloszynski T, Podsiadlo P, Stachowiak GW, Kurzynski M, Lohmander LS, Englund M. Prediction of progression of radiographic knee osteoarthritis using tibial trabecular bone texture. Arthritis Rheum. 2012;64:688–95.
Babitt JL, Zhang Y, Samad TA, Xia Y, Tang J, Campagna JA, et al. Repulsive guidance molecule (RGMa), a DRAGON homologue, is a bone morphogenetic protein co-receptor. J Biol Chem. 2005;280:29820–7.
Xia Y, Yu PB, Sidis Y, Beppu H, Bloch KD, Schneyer AL, et al. Repulsive guidance molecule RGMa alters utilization of bone morphogenetic protein (BMP) type II receptors by BMP2 and BMP4. J Biol Chem. 2007;282:18129–40.
Brown SDM, Moore MW. The International Mouse Phenotyping Consortium: past and future perspectives on mouse phenotyping. Mamm Genome. 2012;23:632–40.
Lepus CM, Song JJ, Wang Q, Wagner CA, Lindstrom TM, Chu CR, et al. Brief report: carboxypeptidase B serves as a protective mediator in osteoarthritis. Arthritis Rheumatol (Hoboken, NJ). 2014;66:101–6.
Gutierrez GM, Kong E, Sabbagh Y, Brown NE, Lee J-S, Demay MB, et al. Impaired bone development and increased mesenchymal progenitor cells in calvaria of RB1-/- mice. Proc Natl Acad Sci U S A. 2008;105:18402–7.
Spector TD, Reneland RH, Mah S, Valdes AM, Hart DJ, Kammerer S, et al. Association between a variation in LRCH1 and knee osteoarthritis: a genome-wide single-nucleotide polymorphism association study using DNA pooling. Arthritis Rheum. 2006;54:524–32.
Jiang Q, Shi D, Nakajima M, Dai J, Wei J, Malizos KN, et al. Lack of association of single nucleotide polymorphism in LRCH1 with knee osteoarthritis susceptibility. J Hum Genet. 2008;53:42–7.
Snelling S, Sinsheimer JS, Carr A, Loughlin J. Genetic association analysis of LRCH1 as an osteoarthritis susceptibility locus. Rheumatology (Oxford). 2007;46:250–2.
Hiram-Bab S, Liron T, Deshet-Unger N, Mittelman M, Gassmann M, Rauner M, et al. Erythropoietin directly stimulates osteoclast precursors and induces bone loss. FASEB J. 2015;29:1890–900.
Rüegsegger P, Koller B, Müller R. A microtomographic system for the nondestructive evaluation of bone architecture. Calcif Tissue Int. 1996;58:24–9.
Hildebrand T, Laib A, Müller R, Dequeker J, Rüegsegger P. Direct three-dimensional morphometric analysis of human cancellous bone: microstructural data from spine, femur, iliac crest, and calcaneus. J Bone Miner Res. 1999;14:1167–74.
Hall M, Manship G, Morahan G, Pettit K, Scholten J, Tweedie K, et al. The genome architecture of the Collaborative Cross mouse genetic reference population. Genetics. 2012;190:389–401.
Mott R, Talbot CJ, Turri MG, Collins AC, Flint J. A method for fine mapping quantitative trait loci in outbred animal stocks. Proc Natl Acad Sci U S A. 2000;97:12649–54.
Acknowledgements
This study was supported by Tel Aviv University starter funds and by Israel Science Foundation (ISF) Grant No. 1822/12 to YG, by Wellcome Trust grants 085906/Z/08/Z, 075491/Z/04, and 090532/Z/09/Z to RM, and core funding by Tel-Aviv University to FI.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
RL developed the study design, performed data acquisition and statistical analyses, and drafted the manuscript. RM developed tools for data analysis and drafted the manuscript. FI developed and planned the study design and drafted the manuscript. YG conceived and directed the study, developed tools for data analysis, and drafted the manuscript. All authors read and approved the final manuscript.
Additional files
Additional file 1: Figure S1.
Phenotypic diversity between the CC lines. (A) phenotypic distribution among males and (B) females. From top-left, counter-clockwise: trabecular bone volume fraction (BV/TV; %), trabecular number (Tb.N; mm-1), thickness (Tb.Th; mm), and connectivity density (Conn.D; mm-3). (DOC 400 kb)
Additional file 2: Table S1.
Trait means. Table S2. Trait correlations. Table S3. Candidate genes. (XLSX 17 kb)
Additional file 3: Figure S2.
Haplotype mapping for the albino trait using 38 CC lines. Plots show –logP values (y-axis) according to chromosome location (x-axis). Horizontal line represent, top-to-bottom, the 95th, 90th, and 50th percentile thresholds, respectively. Peak is at 7.69 –logP. (PDF 54 kb)
Additional file 4: Figure S3.
Confidence-interval simulations for QTL. Loci at a neighborhood of 3-5 Mb around the original locus were simulated by permuting the residual sum of squares of the related phenotype. Maximum logP was obtained along with its relative position in Mb to the original QTL (histograms, left panels), and with the number of markers from the original QTL (boxplots, right panels). Simulations results for the BV/TV loci (Trl1 and Trl2), determined with high confidence that the peak QTL is responsible for the effect seen in the haplotype scan, thus the narrow CI; Trl3 histogram and corresponding boxplot represent simulation results for Tb.N; plots for Trl4 and Trl5 show simulations for Tb.Th; and Trl6 for Conn.D. Note the narrow CI for Trls 1, 2 (BV/TV), 4, and 5 (Tb.Th), wide for Trl3 (Tb.N), and wider still for Trl6 (Conn.D). (PDF 113 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.
About this article
Cite this article
Levy, R., Mott, R.F., Iraqi, F.A. et al. Collaborative cross mice in a genetic association study reveal new candidate genes for bone microarchitecture. BMC Genomics 16, 1013 (2015). https://doi.org/10.1186/s12864-015-2213-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12864-015-2213-x