Introduction

Food production and crop growth depend on rainfall [30]. Excessive rainfall can lead to floods, landslides, and other natural disasters. Accurate rainfall prediction is essential for monitoring water resource sources [12, 34]. Urban planners use rainfall predictions to design drainage systems [14, 15]. Rainfall predictions can be used to study the effects of climate change on different regions of the world [10, 44]. Predicting and mitigating floods requires timely and accurate rainfall predictions. We need accurate rainfall predictions to fully understand climate patterns [41]. To assess the impact of changing weather patterns on ecosystems and communities, scientists use rainfall prediction data.

Rainfall prediction is complex because numerous factors influence rainfall patterns [5, 6, 8]. Local factors such as urbanization and land use changes can influence microclimates and rainfall patterns [1]. In order to accurately predict rainfall, these factors must be considered.

Machine learning (ML) model is a valuable tool for predicting rainfall. Machine learning models can update their predictions as new data becomes available [1, 16] Machine learning models can process large and diverse data sets, including historical weather data, radar data, and various atmospheric parameters [3, 24]. A random forest (RF) model is a simple and accurate machine learning model [2, 28]. The RF has a simple structure and high accuracy. Scholars have used the RAF model to classify and predict data.

Yu et al. [39] developed the support vector machine (SVM) and RF models to predict rainfall. The accuracy of the RF model decreased as the time horizon increased. Ali et al. [2] combined complete ensemble empirical mode decomposition (CEEMD) with the RF model to predict monthly rainfall. Time series data were decomposed into intrinsic mode functions (IMFs). The study results indicated that the CEEMD–RF successfully predicted rainfall values. Shijun et al. [33] compared the RF and the support vector machine model (SVM) for predicting rainfall. The study concluded that the RF model was more accurate than the SVM model. Singh et al. [32] developed the RAF and SVM model to predict runoff. They reported that the RF was successful in predicting runoff. Qiao et al. [29] coupled the RF model with the temporal convolutional network (TCN) to identify the most important predictors for rainfall prediction. The study results indicated that the RAF–TCN provided high accuracy for rainfall predictions. Vergni and Todisco [35] developed the RF model to predict soil loss. They used the runoff coefficient and the period of occurrence to predict soil loss. The study results showed that the RF model could successfully estimate soil loss.

Although the RAF model successfully predicts rainfall time series, it has some limitations. The RAF model lacks advanced operators to capture temporal dependencies [44]. Time series data may have irregular intervals or missing values, but the RF model may not process them. This paper addresses the shortcomings of the RF and predicts monthly rainfall data. The main innovations of the study are the development of a new model for spatial and temporal rainfall predictions and the creation of a new hybrid optimization algorithm for choosing inputs. The new optimization algorithm can reduce the complexity of the feature selection process because it selects the most important features.

Recent studies have indicated that deep learning models are reliable tools for extracting important information from data and improving the performance of classical machine learning models such as random forest models and regression models [1, 18]. Temporal convolutional network (TCN) is a deep learning model that processes sequential data. TCNs use convolutional layers to extract features from sequential data [18, 19]. These convolutional layers can capture local patterns from input sequences [37, 38]. A dilated convolution can capture long-term dependencies.

As deep learning models use advanced operators and different computational layers for processing data, they can enhance the performance of classical machine learning models [1, 37, 38]. A TCN model includes multiple layers that extract features from data and process a large number of data. These features make TCN ideal for coupling with classical machine learning models and improving their performance. Our study uses the capabilities of the TCN model to enhance the performance of the RF model. The TCN–RF model predicts data and extracts features. The TCN model can be used as a feature extractor to improve the performance of the RAF model for predicting time series. The TCN model utilizes one-dimensional convolutional layers to process sequential data [43]. Rainfall patterns often exhibit non-linear dependencies over time. Linear models may not be able to capture these complex relationships. The TCN model can effectively capture the temporal dependencies of the rainfall time series. TCN can act as a feature extractor. It can automatically learn relevant features from the rainfall time-series data.

In this study, we develop and introduce a novel TCN model that is combined with the RF model and predicts rainfall data. The original TCN model may not be able to identify and remove unnecessary or redundant features from time-series data. The irrelevant and redundant features can influence the accuracy of the TCN model. Irrelevant features may contain misleading information. If the TCN model uses unnecessary and redundant features, it may learn incorrect patterns. Our study addresses this drawback of the TCN model.

Our study introduces a novel technique called a deep residual shrinkage network (DRSN) to address the limitations of the TCN model. The DRSN model is inserted into the residual connections of the TCN model. Since the DRSN model removes redundant and irrelevant features, it enhances the quality of the extracted features [11]. The DRSN uses a soft thresholding operator to remove irrelevant features. [4]. The TCN model can improve its prediction accuracy as it focuses on the key features and reduces irrelevant features. The soft thresholding operator deletes features whose absolute values ​​are below the threshold T and shrinks features whose absolute values are above the threshold T. Since selecting input features and predicting rainfall and non-linear patterns is complex and difficult, we need advanced tools to accurately predict rainfall patterns. This article introduces an effective mechanism for removing irrelevant data and improving the performance of machine learning models. The DRSN was introduced to address this issue. Also, the hybrid TCN–RF model can capture spatiotemporal patterns and make accurate rainfall predictions. Thees a new robust optimizer for feature selection and reduce the complexity of the problem.

The current paper contains the following innovations:

  • The paper introduces the TCN–RF model to enhance the efficiency of the RF model for monthly rainfall prediction. The TCN extracts features and sends them to the RF model for rainfall prediction. No study has developed the TCN–RF model to predict rainfall data.

  • Our study develops the TCN model for identifying important features. A DRSN–TCN–RF (DTR) predicts rainfall data and removes redundant and irrelevant features. The DRSN–TCN is a novel deep learning model for processing data.

  • The choice of input selection plays a key role in rainfall prediction. Binary optimizers are robust tools for choosing inputs. Moreover, we need a robust optimizer to set the model parameters. Scholars have developed different optimizers to solve optimization problems in recent years. Jiang et al. [13] introduced a novel optimization algorithm named the orca predation algorithm (OPA) to solve complex problems. It was inspired by the hunting behavior of orcas. Compared to other algorithms, the OPA produced better results. The OPA may get stuck in local optima when an optimization problem involves a large number of decision variables and constraints. Our study develops the OPA to address this issue. Jiang et al. [13] introduced the continuous version of the OPA to solve complex problems. Since we need binary versions of optimization algorithms for feature selection, we convert the continuous version of the OPA into a binary version of the OPA. The process of feature selection involves binary decision variables. We use a new binary algorithm to identify the best input scenarios.

Details of the models are presented in the following section. In addition, the fourth and fifth sections will discuss the results. Finally, the sixth section concludes and presents suggestions for the next paper.

Materials and methods

Random forest model

A random forest model consists of several decision trees. The prediction process begins with collecting input and output data [22]. The dataset is cleaned to handle missing values, outliers, and inconsistencies [20]. Multiple decision trees are trained on different subsets of the training data. Decision trees are created recursively. The algorithm selects the best features and divides the nodes of each decision tree based on a criterion such as Gini impurity (for classification) or mean squared error (for prediction) [42]. The root node of a decision tree is the first node. The root node is split into child nodes based on particular features and splitting criteria [42]. The model divides nodes until a stopping criterion is met. The stop creation can be determined by a maximum depth, a minimum number of samples, or other factors. After we create all the individual decision trees, we have an ensemble structure. The ensemble structure combines individual predictions to make a final prediction for each data point.

TCN model

TCNs can capture both short- and long-term dependencies. TCNs use residual connections to propagate gradients and improve model convergence. The TCN model consists of convolutional layers [43]. The convolutional layer processes sequential data. Each convolutional layer has a set of filters that slide (convolve) over the input sequence to extract local patterns and features [37, 38]. Causal convolution is the next component of TCNs that capture temporal dependencies of sequential data [18, 19]. Causal convolutions prevent information leakage from future time steps. Causal convolutions use dilated convolutions to capture temporal dependencies and efficiently cover distant parts of input sequences. A convolutional filter can capture both short-term and long-term dependencies when the dilation rate is higher than 1. The receptive field of a convolutional filter refers to the region of the input sequence that affects the output of that particular filter. A residual connection is the next component of the TCN model.

Residual or skip connections are commonly employed to tackle the vanishing gradient problem and train deep TCN architectures [18, 19]. The TCN models can use max-pooling or average-pooling layers to down sample the outputs. The pooling layer can reduce the spatial dimensionality of feature maps [17]. TCNs typically have an output layer that produces predictions after the input sequence is processed by convolutional layers.

Hybrid DRSN–TCN model

The DRSN–TCN (DRT) is a deep learning model designed for predicting time-series data. DRSN inserts a soft thresholding mechanism into the residual connections of the traditional TCN model. A soft thresholding technique reduces irrelevant information. This method eliminates or shrinks redundant features. We drop features whose absolute values are below a threshold and shrink features whose absolute values are above the threshold. DRSN uses subnetworks for threshold estimation. These subnetworks receive the absolute value of each element of the output matrix and apply global average pooling to obtain mean values for each channel. Based on a sigmoid activation function, threshold values are scaled between 0 and 1. The hybrid model consists of multiple components. An inflated causal convolution layer is the first component of the hybrid model. Causal convolutions ensure that outputs depend only on past and present inputs. Dilated convolutions increase the receptive field gradually. At the next level, a threshold estimation building unit is employed to estimate thresholds for feature shrinkage. Feature shrinkage reduces the dimension of the feature space and preserves relevant information. The threshold estimation building unit computes the absolute value of each element of the output matrix of the causal convolution layer [11]. The DTR uses this strategy to ensure that each threshold is positive [4]. Once we get the absolute values, we apply one-dimensional global average pooling to the output matrix. Global average pooling computes the mean value of the features to downsize the feature map. The one-dimensional vector of the mean values of each feature map is used as input for later thresholding. Each feature map will be shrunk using these thresholds. We set feature values below the threshold to zero to reduce redundant features. Soft thresholding is computed as follows:

$$z = \left[ \begin{gathered} x - \varphi \leftarrow x > \varphi \hfill \\ 0 \leftarrow - \varphi \le x \le \varphi \hfill \\ x + \varphi \leftarrow x < - \varphi \hfill \\ \end{gathered} \right],$$
(1)

where \(x\)is the input feature, z is the output, and \(\varphi\) is the threshold value.

Optimization algorithms for feature selection

Orca optimization algorithm (OPA)

Orcas are intelligent and social mammals. They are the largest members of the dolphin family [13]. Typically, an orca group consists of three members: calves (20%), adult males (20%), and females (60%). A male may leave a social group if it becomes too large. Orcas emit sounds such as clicks, whistles, and pulsed calls, into the water to precisely determine the location and distance of potential prey [13]. To locate prey and communicate with each other, orcas use sonar. Orcas confine their prey to the surface of the water. Orcas employ a variety of tactics to stun or incapacitate fish. They hit the fish with their powerful tails. First, we initialize a group of orcas as follows:

$$OR = \left( {or_{1} ,..,or_{N} } \right),$$
(2)

where \(OR\): a group of orcas, \(or_{1}\): The location of the first orca, \(or_{N}\): The location of the Nth orca. Orcas use echolocation to locate their prey and communicate with group members. They emit different types of vocalizations, including clicks, whistles, and pulsed calls, to transfer information to each other [13]. Orcas use vocalizations to coordinate their actions during hunting and to maintain social bonds. The orcas employ a variety of strategies, including echolocation (sonar), coordinated swimming, and communication, to drive the school of fish to the surface of the water. Once the school of fish approaches the surface, the orcas create a controlled enclosure around the fish [13]. A group of orcas surrounds the fish. Orcas employ strategies such as driving and encircling prey to catch their prey.

Driving of prey

The small groups of orcas locate and hunt the school of fish efficiently (First scenario). Large groups of orcas may reach the desired position (Second scenario). When the orca group is large, the spatial dimension of swimming is high. Orcas change their location based on the size of their population [13]

$$VE_{chase,1,i} = \mu \times \left( {\beta \times OR_{best}^{t} - F \times \left( {\varphi \times J^{t} + b \times OR_{i}^{t} } \right)} \right),$$
(3)
$$VE_{chase,2,i} = e \times OR_{best}^{t} - OR_{i}^{t} ,$$
(4)
$$J = \frac{{\sum\limits_{i = 1}^{N} {OR_{i}^{t} } }}{N},$$
(5)
$$b = 1 - \beta ,$$
(6)
$$\left[ \begin{gathered} OR_{chase,1,i} = OR_{I}^{t} + VE_{chase,1,i}^{t} \leftarrow if\left( {rand} \right) > u \hfill \\ OR_{chase,1,i} = OR_{I}^{t} + VE_{chase,1,i}^{t} \leftarrow if\left( {rand} \right) \le u \hfill \\ \end{gathered} \right],$$
(7)

where \(OR_{chase,1,i}\) is the location of orca based on the first scenario, \(OR_{chase,1,i}\) is the location of orca based on the second scenario, u is the random number, N is the number of orcas, \(VE_{chase,1,i}\) is the velocity of orca based on the first scenario, \(\beta\) is the random number, \(VE_{chase,2,i}\)is the velocity of orca based on the second scenario, \(F\)is the controller parameter (F = 2), \(\mu\) is the random parameter, e is the random number, \(OR_{best}^{t}\)is the location of best orca, and J is the average location of one group.

Encircling of prey

Fish schools cannot move in different directions because orcas surround them. Orcas often use vocalizations to coordinate their movements and determine their next position. They change their location based on the locations of three randomly selected orcas [13].

$$RO_{chase,3,i,k}^{t} = RO_{j1,k}^{t} + \chi \times \left( {RO_{j2,k}^{t} - RO_{j3,k}^{t} } \right),$$
(8)
$$\chi = 2 \times \left( {rand - \frac{1}{2}} \right) \times \frac{{\max \left( {it} \right) - t}}{{\max \left( {it} \right)}},$$
(9)

where \(RO_{chase,3,i,k}^{t}\) is the new location of orcas, \(RO_{j1,k}^{t}\), \(RO_{j2,k}^{t}\), and \(RO_{j3,k}^{t}\) is the random location of orcas,, rand is the random number, \(\max \left( {it} \right)\) is the maximum number of iterations, and t is the iteration number. The orcas will update their location if they achieve a better objective function value at a new location.

$$\left[ \begin{gathered} OR_{chase,i}^{t} = OR_{chase,i}^{t} ,if \to f\left( {OR_{chase,i}^{t} } \right) < f\left( {OR_{i}^{t} } \right) \hfill \\ OR_{chase,t}^{t} = OR_{i}^{t} ,if \to f\left( {OR_{chase,i}^{t} } \right) \ge f\left( {OR_{i}^{t} } \right) \hfill \\ \end{gathered} \right],$$
(10)

where \(f\left( {OR_{chase,i}^{t} } \right)\) is the objective function of the new location of the orca, \(f\left( {OR_{i}^{t} } \right)\) is the objective function value of the current location of the orca.

Attacking preys

A group of orcas forms an enclosure or barrier to capture prey. After the orca enters the enclosure to attack prey, it whips or stuns the fish with its tail. The OPA hypothesizes that four orcas have the best locations in the enclosure [13]. The other orcas update their direction based on the locations of the four orcas that enter the enclosure. After eating their prey, orcas return to their original position and replace another orca [13]. At this level, orcas adjust their direction of movement based on the positions of nearby orcas, which are randomly placed in the search area. The final location and speed of the orcas are determined using the following equations:

$$VE_{attack,1,i} = \left( {OR_{first}^{t} + OR_{\sec ond}^{t} + OR_{third}^{t} + OR_{fourth}^{t} } \right),$$
(11)
$$VE_{attack,2,i} = \left( {OR_{chase,j1}^{t} + OR_{chase,j2}^{t} + OR_{chase,j3}^{t} } \right),$$
(12)
$$OR_{attack,i}^{t} = OR_{chase,i} + \alpha_{1} \times VE_{attack,1,i} + \alpha_{2} \times VE_{attack,2,i} ,$$
(13)

where \(VE_{attack,1,i}\) is the speed of the ith orca; \(VE_{attack,2,i}\) is the speed of the ith orca at the enclosure; \(OR_{first}^{t}\), \(OR_{\sec ond}^{t}\), \(OR_{third}^{t}\), \(OR_{fourth}^{t}\) are the location of the first, second, third, fourth orca; \(OR_{chase,j1}^{t}\), \(OR_{chase,j2}^{t}\), and \(OR_{chase,j3}^{t}\) are the random locations of orcas; \(OR_{attack,i}^{t}\) is the final location of orca; \(\alpha\) and \(\alpha_{2}\) are the random numbers. The optimization process begins with creating an initial population of orcas. Then, we use Eqs. 3–10 to update the position and speed of orcas. Finally, we update the location of the orcas based on the attacking prey.

Improved OPA

Our study introduces a novel technique to tackle the problem of premature convergence and local optima of OPA. A feature selection problem may contain a large number of decision variables, so the OPA may get stuck in local optima. Premature convergence is also another disadvantage of the OPA. A novel approach is used to address the shortcomings of the OPA. To increase the diversity of solutions and avoid local optima, we used the Gaussian mutation method. The Gaussian mutation (GM) produces new solutions that follow the characteristics of the normal distribution [40]. The proposed solutions are placed near the original solutions [40]. Thus, the Gaussian mutation improves the exploitation ability of the OPA. As the Gaussian mutation produces new solutions, it can improve the ability of the OPA to avoid trapping in local optima. The GM also helps the OPA identify promising regions.

$$f_{G} = \frac{1}{{\sqrt {2\pi } \sigma }}epx\left( { - \frac{{\left( {z - \mu } \right)^{2} }}{{2\sigma^{2} }}} \right),$$
(14)
$$OR_{G} \left( {t + 1} \right) = G\left( {OR_{\mu } ,OR_{{\sigma^{2} }} } \right),$$
(15)
$$OR_{\mu } = \frac{{OR_{best} \left( t \right) + OR\left( t \right)}}{2},$$
(16)
$$OR_{{\sigma^{2} }} = \left| {OR_{best} - OR_{t} } \right|,$$
(17)

where \(G\left( {OR_{\mu } ,OR_{{\sigma^{2} }} } \right)\) is a random number, \(OR_{\mu }\) is the mean of the Gaussian mutation, \(OR_{{\sigma^{2} }}\) is the variance of the Gaussian mutation, x is the random variable, \(\sigma\) is the variance of random variable, \(\mu\) is the mean of random variable, \(OR_{best} \left( t \right)\) is the best position of orca, and \(OR\left( t \right)\) is the current location of orca. The new algorithm is named GM–OPA. Our study compares new optimization algorithms with multiple optimization algorithms.

Particle swarm optimization algorithm (PSO).

PSO is one of the practical optimization algorithms for solving complex problems. The best particle guides the swarm particle toward the best location [26]. Particles are characterized by their velocity and position [27]. The particles change their components as follows:

$$ve_{i} \left( {t + 1} \right) = \varepsilon ve_{i} \left( t \right) + \tau_{1} r_{1} \left[ {p_{i} - s_{i} } \right] + \tau_{2} r_{2} \left[ {p_{g} - s_{i} } \right],$$
(18)
$$s_{i} \left( {t + 1} \right) = s_{i} \left( t \right) + ve_{i} \left( {t + 1} \right),$$
(19)

where \(ve_{i} \left( {t + 1} \right)\) is the ith velocity at iteration (t + 1), \(s_{i} \left( t \right)\) is the ith solution, \(r_{1}\) and \(r_{2}\) are the random numbers, \(p_{i}\) is the local best solution, and \(p_{g}\) is the global best solution, \(s_{i} \left( t \right)\) is the ith solution, and \(s_{i} \left( {t + 1} \right)\) is the new solution, \(\tau_{1}\) and \(\tau_{2}\)are the learning factors, and r1 and r2 are the random numbers, and \(\varepsilon\) is the weight coefficient.

Crow optimization algorithm (COA)

The COA was inspired by the life of crows [31]. Crows hide their food in a safe place. Each crow may pursue other crows to steal their food. First, we initialize the location of the crows as follows: [21]:

$$CR_{j}^{it} = \left[ {CR_{1}^{i} ,CR_{2}^{i} ,..,CR_{d}^{i} } \right],$$
(20)

where \(CR_{j}^{it}\) is the ith location of crow in the jth dimension and d is the number of dimensions. The COA uses a memory to save the best solutions:

$$M_{j}^{i} = \left[ {m_{1}^{i} ,m_{2}^{i} ,..,m_{d}^{i} } \right],$$
(21)

where \(M_{j}^{i}\) is the ith memory in the jth dimension. The crow search algorithm (COA) uses two scenarios to find optimal solutions. The first scenario assumes that the first crow knows that the second crow is following it. The first crow deceives the second crow. The first crow updates its location based on the following equation.

$$X_{j}^{t + 1} = \left[ \begin{gathered} X_{j}^{t} + r_{i} \times fl_{j}^{t} \times \left( {M_{i}^{t} - X_{j}^{t} } \right) \leftarrow r_{j} \ge AP_{j}^{t} \hfill \\ Select\left( a \right)\left( {random} \right)\left( {location} \right) \hfill \\ \end{gathered} \right],$$
(22)

where \(X_{j}^{t + 1}\) is the jth location at t + 1 iteration, \(M_{i}^{t}\) is the ith memory at iteration t, \(AP_{j}^{t}\) is the awareness probability of the crow j, \(r_{i}\) is the random number, \(Y_{j}^{t}\) is the current location of crow. The second scenario assumes that the first crow does not know that the second crow is following it. The second crow update its locations based on the following equation [9]:

$$X_{j}^{t + 1} = X_{j}^{t} + r_{j} \times fl_{j}^{t} \times \left( {M_{i}^{t} - X_{j}^{t} } \right),$$
(23)

where \(X_{j}^{t + 1}\) is the new location of the jth crow. The COA updates the memory using Eq. 24:

$$M_{{}}^{t + 1} = \left[ \begin{gathered} X_{i}^{t + 1} \leftarrow fitness\left( {X_{i}^{t + 1} } \right) > X_{i}^{t} \hfill \\ M_{i}^{t} \hfill \\ \end{gathered} \right].$$
(24)

The first step is to define the initial positions of the crows. The objective function value is used to determine the best crow. Then, we use one of the scenarios to update the crow location. The memory is updated at each level. The process continues until the convergence criteria are met.

Sine cosine optimization algorithm (SCOA)

SCA uses cosine and sine functions to search for optimal solutions. First, we define the initial solutions for the optimization process [25]. At the next level, the objective function value is calculated to evaluate the quality of the solutions. Equations 25 and 26 are used to update the values of solutions [7].

$$SO_{i}^{t + 1} = \left[ \begin{gathered} SO_{i}^{t} + \upsilon_{1} \times \sin \left( {\upsilon_{2} } \right) \times \left| {\upsilon_{3} SO_{ig}^{t} - SO_{i}^{t} } \right|,\nu_{4} \le 0.50 \hfill \\ SO_{i}^{t} + \upsilon_{1} \times \cos \left( {\upsilon_{2} } \right) \times \left| {\upsilon_{3} SO_{ig}^{t} - SO_{i}^{t} } \right|,\nu_{4} > 0.50 \hfill \\ \end{gathered} \right],$$
(25)

where \(SO_{i}^{t + 1}\) is the new solution, \(\upsilon_{1}\), \(\upsilon_{2}\), \(\upsilon_{3}\), and \(\nu_{4}\) are the random values, and \(SO_{ig}^{t}\) is the best solution. The \(\upsilon_{1}\) is computed using the following equation:

$$\nu_{1} = \kappa - \frac{t}{T}\kappa ,$$
(26)

where \(\kappa\) = 2, t is the iteration number, and T is the maximum number of iterations.

Binary optimization algorithms

We use a binary optimization algorithm for feature selection. To convert continuous versions of OPA, SCOA, PSO and COA into binary versions, the transfer functions are used. Our research uses an S-shaped transfer function to convert a continuous version into a binary version. It was reported that the S-shaped transfer function had the highest accuracy for solving complex problems.

$$S\left( {SO_{m,j}^{t} } \right) = \frac{1}{{1 + e^{{ - x_{m,j}^{t} }} }},$$
(27)
$$SO_{m,j}^{t} = \left[ \begin{gathered} 1 \leftarrow rand < S\left( {SO_{m,j}^{t} } \right) \hfill \\ 0 \leftarrow rand \ge S\left( {SO_{m,j}^{t} } \right) \hfill \\ \end{gathered} \right],$$
(28)

where \(SO_{m,j}^{t}\) is the jth solution and \(S\left( {SO_{m,j}^{t} } \right)\) is the transfer function.

Hybrid GE–POA DTR model

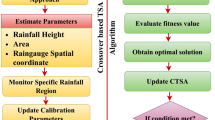
Our study uses the GE–POA–DTR to monthly rainfall. One of the main advantages of the new model is that it can capture spatiotemporal patterns. The new model can be used in different climates. The classical machine learning models are sensitive to irrelevant features. These features may reduce the accuracy of machine learning models. The DRSN–TCN–RF (DTR) model is a robust model for handling complex data sets as it discards irrelevant data. We follow the following levels to create the new model:

  • Determining the data size is essential for running models at the training and testing levels. The K-fold cross-validation method (KSV) is a suitable tool for classifying data into training and testing data. Data points are divided into distinct groups using K folds [36]. Then, predictive models are executed k times. The error function values are calculated for each run [23]. To evaluate the performance of models in predicting output, the average error function value is computed. K-fold cross-validation is a valuable technique for preventing overfitting. As the KSV uses different subsets of data to train and test models, it can reduce the risk of overfitting.

  • The decision variables are defined. The input names and model parameters are decision variables. The initial algorithm population consists of these decision variables.

  • The DRSN–TCN model is executed and an error function is calculated to evaluate its performance. Based on threshold values, the DRSN model determines important features. The TCN then uses the key features to predict rainfall patterns.

  • If the stop criterion is met, the model will enter the testing level; otherwise, we link the DRSN–TCN model with the optimizers. Operators of optimizers are used to update the input combination and model parameters. The process continues until the convergence criterion is achieved.

  • The testing data are used to run the DRSN–TCN model.

  • The outputs of the DRSN–TCN are used as inputs to the RF model. The RF model is used to predict monthly rainfall data at training and testing levels.

Appendix A: Table 3 shows list of variables.

Case study

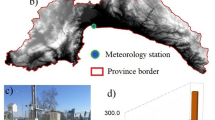
The Kashan Plain is a plain in central Iran. The Kashan Plain is characterized by a dry climate and desert and semi-desert landscapes. The summers are hot and dry, while the winters are cool. Traditional techniques such as qanats (underground water channels) are used to meet water needs. In the Kashan plain, irrigation and crop production depend on rainfall. Rainfall is an important source of water in the Kashan Plain. The data were collected from 1992 to 2015. April, May, and June are the wettest months, while July, August, and September are the driest months. Kashan Plain experiences high temperatures during summer. The average daily temperature ranges from 30 to 40 degrees Celsius. Monthly rainfall varies from 0 to 134 mm. Figure 1a shows the plain location. Figure 1b displays the location of the stations. Figure 1c displays time-series data. We used lagged rainfall data to predict one-month ahead rainfall. The lag times of (t-1) to (t-12) were used to predict outputs. Rainfall often exhibits temporal patterns and dependencies. Lagged rainfall data capture these temporal relationships. Historical data sets are required for training predictive models. Machine learning models require past data to learn the underlying patterns and relationships. A predictive model can gain a better understanding of historical patterns by considering lagged rainfall data. Seven stations were used because the new model could achieve the lowest values of the error function. The Thiessen polygon method was used to determine the average monthly rainfall values for the entire catchment area. The basin was divided into several polygons. Weight coefficients were assigned to the polygons to obtain average precipitation values (Table 1).

Fig. 1
figure 1

. a Location of plain on Iran map, b location of stations, and c time-series data

Full size image
Table 1 The details of data points
Full size table

We collect monthly rainfall data from monitoring stations. We identify the basin boundary, which is used for creating Thiessen polygons. A Thiessen Polygon (Voronoi Polygon) is created around each monitoring station. We calculate the area of each Thiessen polygon. The area of each polygon represents the influence zone of the corresponding monitoring station. The weight of each polygon is calculated by estimating its area. These weights are multiplied by observed rainfall values at monitoring stations. To estimate monthly rainfall for the entire basin area, we sum the weighted rainfall values of all monitoring stations for each month. To assess the efficiency of models, the following error functions are used:

Willmott index

$$WI = 1 - \frac{{\sum\limits_{j = 1}^{n} {\left( {RI_{iob} - RI_{ies} } \right)^{2} } }}{{\sum\limits_{i = 1}^{n} {\left( {\left| {RI_{iob} - \overline{R}I} \right| + \left| {RI_{ies} - \overline{R}I} \right|} \right)^{2} } }}.$$
(29)

Root mean square error (RMSE)

$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {RI_{ob} - RI_{es} } \right)}^{2} } .$$
(30)

Mean absolute error (MAE)

$$MAE = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {OC_{es} - OC_{ob} } \right|} .$$
(31)

Percent bias (PBIAS)

$$PBIAS = \frac{{\sum\limits_{i = 1}^{N} {\left( {RI_{ob} - RI_{es} } \right)} }}{{\sum\limits_{i = 1}^{N} {RI_{ob} } }}.$$
(32)

U95

$$U_{95} = 1.96\left( {SD^{2} + RMSE} \right)^{\frac{1}{2}} ,$$
(33)

where \(RI_{ob}\) is the observed rainfall, \(RI_{es}\) is the estimated rainfall, \(SD\) is the standard deviation, \(\overline{R}I\) is the average observed rainfall. Our study also uses Eq. 34 to evaluate the ability of optimization algorithms in choosing inputs:

$$Average\left( {selection\left( {size} \right)} \right) = \frac{1}{M}\sum\limits_{i = 1}^{M} {\frac{{size\left( {so^{i} } \right)}}{NU}} ,$$
(34)

where M is the number of runs, NU is the number of total inputs, and \(size\left( {so^{i} } \right)\) is the size of chosen inputs at each run. The best algorithm has the lowest value of average selection size (ASS).

Results

Determination of number of K

Calculating K is necessary for the modeling process and splitting the data into training and testing data points. Figure 2 shows the RMSE values for different K numbers. The DTB model was used based on different sizes of K. K = 10, K = 5, and K = 2 provided RMSE values of 0.187–0.235, 0.187–0.270, and 0.189–0.276, respectively. Thus, we chose K = 10 to run models.

Fig. 2
figure 2

The determination of K

Full size image

Computation of the values of random parameters

Adjusting the random parameters is necessary to achieve the highest accuracy of optimizers. Optimal parameter values minimize the RMSE of optimizers. The maximum number of iterations (MNI) is one of the most important random parameters. Population size (PS) also changes the accuracy of optimizers. The GM–OPA and OPA had the best performance (lowest RMSE) based on PS = 120 and MNI = 300. PS = 180 and MNI = 300 provided the highest precision for the SCOA (Fig. 3).

Fig. 3
figure 3

Determination of random parameters

Full size image

Choice of the best optimizers and input scenarios

Figure 4 shows accuracy optimizers for choosing inputs. The RMSE of the GM–OPA varied from 0.180 to 0.200 mm. The GM–OPA reduced the RMSE values of OPA and PSO by 1.4%–3.4% and 6.14–9.54%, respectively. Thus, GM–OPA improved the performance of the ROA.

Fig. 4
figure 4

The spatial values of RMSE of different models

Full size image

Figure 5 shows the percentage of features selected. Also, this figure shows ASS values of different algorithms. The GM–OPA, OPA, SCOA, COA, and PSO chose 33%, 41%, 41%, 50%, and 50% of the total number of inputs. The ASS of the GM–ROA was lower than that of other algorithms. Thus, the GM–ROA achieved the highest accuracy with fewer input variables. The GM–OPA selected rainfall (t-1), rainfall (t-2), and rainfall (t-3) as predictors for rainfall prediction. Table 2 shows the optimal values of hybrid model parameters. The optimization algorithm systematically searches the problem space to find the optimal values of the model parameters. First, we initialize the initial values of the model parameters. The GM–OPA then updates the values of the parameters at each iteration. When the GM–OPA converges to the lowest value of the objective function value, the process is completed. The optimal values of model parameters are reported and used to train and test models. Although there are 212–1 input scenarios, our model chose the optimal input scenario with three input variables. Thus, the optimizers played a key role in reducing the computational cost of the modeling process.

Fig. 5
figure 5

The Percentage of feature selected numbers

Full size image
Table 2 Optimal values of TCN parameters
Full size table

Evaluation of the performance of models

Figure 6 displays the error function values of different models. The DTR reduced the testing MAE values of the TCN–RF, DRSN–TCN, TCN, and RF models by 5.3%, 21%, 40%, and 46%, respectively. The RF provided the highest MAE values. The testing MAE of the RF was 46%, 41%, 32%, and 6.4% was higher than that of the TCN–RF, DTR–TCN, and TCN models. The DRSN model improve the accuracy of the TCN model. The testing MAE of the DRSN–TCN was 28% lower than that of the TCN model. The training NSE of the DTR, TCN–RF, DRSN–TCN, TCN, and RF models was 0.98, 0.95, 0.92, 0.89, and 0.87, respectively. The testing NSE of the DTR and TCN–RF was 0.96 and 0.94. Thus, the DTR and TCN–RF outperformed the other models. The TCN model outperformed the RF model as it used advanced layers and operators for analyzing data. The testing NSE of the TCN model was 3.5% higher than that of the RF model. The DTR model had the best performance as it used the DRSN mechanism to remove irrelevant data.

Fig. 6
figure 6

Error function values of different models

Full size image

The DTR reduced the testing WI values of the TCN–RF, DRSN–TCN, TCN, and RF models by 4.16%, 7.29%, 14%, and 16%, respectively. The training PBIAS of the DTR, TCN–RF, DRSN–TCN, TCN, and RF models was 3, 7, 11, 14, and 18, respectively. The testing U95 of the DTR, TCN–RAF, DRSN–TCN, TCN, and RAF models was 8, 12, 16, 18, and 22, respectively. U95 is an index that can evaluate the accuracy of models based on RMSE and standard devalues. The U95 of the RF model was higher than that of the other models as irrelevant models influence the reliability of the RF model. The DTR model outperformed all models because it leveraged the capabilities of three models. The DRSN component of the DRSN–TCN model employs soft thresholding to identify and eliminate irrelevant features of the rainfall data. The model can control the impact of less relevant features by dynamically setting thresholds. The DRSN–TCN uses soft thresholding to reduce the influence of irrelevant features of a dataset. By effectively reducing irrelevant features, the DRSN–TCN model can improve the generalization ability of the model.

Figure 7 displays heat scatterplots of models. The R2 value of the DTR, TCN–RF, DRSN–TCN, TCN, and RAF models was 0.9916, 0.9848, 0.9791, 0.9691, and 0.9400, respectively. The study results indicated that DTR and TCN–RF performed better than the other models. The DRSN mechanism could improve the performance of the TCN model. The R2 value of the DRSN–TCN model was 1.02% higher than that of the TCN model. However, the irrelevant features reduce the accuracy of the RF model. The RF model had the lowest R2 values among other models.

Fig. 7
figure 7

Heat scatterplots of models

Full size image

Figure 8 displays boxplots of different models. The median of the observed data, DTR, TCN–RF, DRSN–TCN, TCN, and RF models was 55 mm, 59 mm, 61 mm, 63 mm, 64 mm, and 65 mm, respectively. The maximum value of the observed data, DTR, TCN–RF, DRSN–TCN, TCN, and RF model was 134 mm, 134 mm, 134 mm, 134 mm, 135 mm, and 136 mm, respectively.

Fig. 8
figure 8

Boxplots of models for comparing models

Full size image

The study results revealed that the DTR had the best performance among the other models. The DRSN was introduced to address the limitations of the TCN model and improve the quality of the extracted features. The DRSN ensures that the hybrid model concentrates on the most relevant information, which results in more accurate predictions. In summary, the DRSN–TCN–random forest model outperforms the TCN and RAF models because it enhances the quality of extracted features, focuses on relevant information, and enhances efficiency. The TCN model captures non-linear relationships.

Our study developed the GM–OPA to set parameter values and select the best input scenario. As the GM improved the ability of the POA to locally and globally search the problem space, it outperformed other optimizers. The GM–OPA chose the best input scenario based on the fewest number of input variables.

Taylor diagram is a graphical tool for evaluating the performance of the models. At the center of the diagram, a point is represented as the reference dataset. The radial axis represents the standard deviation. The tangential axis represents the correlation coefficient. Contour lines represent centralized root mean square (CRMSE) values. Figure 9 shows a Taylor diagram to compare models at the testing level. The CRMSE of DTR, TCN–RF, DRSN–TCN, TCN, and RF was 0.15, 0.19, 0.26, 0.39, and 0.56, respectively. The correlation coefficients of DTR, TCN–RF, DRSN–TCN, TCN, and RF were 0.99, 0.98, 0.97, 0.92, and 0.84, respectively. The CRMSE and correlation values indicated that the DRSN mechanism improved the performance of the TCN model. The DRSN–TCN improved the CRMSE and correlation values of the TCN model by 19% and 5%, respectively. The RF model provided the highest CRMSE model. The DTR model improved the CMRSE of the RF model by 73%.

Fig. 9
figure 9

Taylor diagram for comparing models

Full size image

Discussion

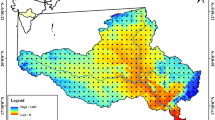
While we use predictive models to predict one-month ahead rainfall, it is required to examine their accuracy for predicting other time horizons. We use the DTR as the best model to predict one-, three-, five-, and seven-month ahead rainfall. Figure 10 shows the spatial accuracy of the DTR model for multi-step-ahead rainfall prediction. The DTR model provided NSE values of 0.87–0.99, 0.82–0.97, 0.79–0.94, and 0.70–0.94 for 1, 3, 5, and 7 months ahead. As the time horizon increases, the efficiency of models decreases. Climate phenomena such as large climate indices can impact long-term patterns. Predicting these large-scale patterns can be difficult and complex. Human activities such as deforestation, urbanization and greenhouse gas emissions can change rainfall patterns over long periods. These factors may increase the uncertainty of long-term rainfall predictions and affect the accuracy of models.

Fig. 10
figure 10

NSE values of different models for predicting different horizon times

Full size image

The DTR model is a useful model as we can use its outputs for water resource management planning and other hydrological simulations. To demonstrate the practical applications of the DT model, we use it to forecast monthly rainfall values for the period 2023–2024. Figure 11 shows the monthly rainfall values for the period 2023–2024. The month of January had the highest rainfall values. In January 2023, 8–40 mm of rainfall fell. The lowest rainfall values were observed in the summer months. In the autumn and winter months, the average rainfall was 21.12 and 18.78 mm, respectively.

Fig. 11
figure 11

Monthly rainfall values for the period 2023–2024

Full size image

Our models also can be used to predict rainfall at different time scales. We use DTR, TCN–RF, DRSN–TCN, TCN, and RF models to predict daily data. Figure 12 displays the absolute relative error (ABR) of daily predictions of different models. The DTR model gave an ABR of 1–5% for 4% of the data points. The RF model gave the highest values of ABR. The MLR model provided an ABR of 19–23% for 10% of the data points. The training NSE of the DTR, TCN–RF, DRSN–TCN, TCN, and RF models was 0.98, 0.95, 0.92, 0.89, and 0.87, respectively.

Fig. 12
figure 12

The ABR of different models for predicting daily data

Full size image

The DTR model effectively removes irrelevant data and extracts temporal features from rainfall data. The DTR model is required for improving prediction accuracy and assessing climate change impact. Our study creates a superior rainfall prediction model, develops innovative optimization techniques, and demonstrates the superior performance of the proposed model. The study findings have practical implications for climate research, water resource management, and disaster preparedness. The new model can be used for understanding water availability, managing reservoirs, and planning for potential floods or droughts. Water resource managers can use the new model to plan for regional variations of rainfall. The model contributes to climate resilience planning as it provides insights into future rainfall trends.

Based on the analysis of the results, the following points should be considered:

  • The GM–OPA can intelligently select a subset of features from the original input space. The algorithm can dynamically adjust the complexity of the model based on the evolving characteristics of the data. The GM–OP can identify and retain only the most relevant features for the target variable. The new algorithm can reduce the dimensionality of the input space as it chooses the most important inputs.

  • Irrelevant features increase the complexity of the model without providing meaningful information. When irrelevant features are removed, the model becomes simpler and focuses on the important features of the data. The DRSN method can reduce the risk of overfitting as it can remove irrelevant features.

  • The DTR–TCN–RF model is a robust model for spatiotemporal predictions. As the TCN model uses convolutional layers and dilated convolutions, it can capture spatiotemporal patterns.

  • The GM–OPA had two main advantages. The algorithm achieved the highest accuracy. Also, the new algorithm chose fewer inputs for predicting rainfall.

  • The study results showed that the RF model could not achieve high accuracy because it could not analyze non-linear patterns.

Conclusion

Accurate rainfall predictions are required for water resources management, including reservoirs, dams, and groundwater recharge. Our study introduced a new model named the DTR to predict 1 month ahead. The DTR consisted of three models. The DRSN was used to remove redundant data. The RAF model received temporal features from the TCN model. Finally, The RF model made rainfall predictions. We developed a novel optimizer called GM–ROA to select inputs. Lagged rainfall values were applied to predict outputs. The study results indicated that GM–ROA improved the ability of the ROA for feature selection. The RMSE of the GM–ROA varied from 0.180 to 200 mm. The GM–ROA reduced the RMSE values of ROA and PSO by 1.4%–3.4% and 6.14–9.54%, respectively. The study results revealed that the DTR outperformed the other models. The DRSN is specifically designed to enhance the quality of the extracted features. The DTR model also could predict daily data with high accuracy. The new model also accurately predicted monthly data for the period 2023–2024. Our study uses the TCN model which processes information in one direction. The execution of these models may have limitations. To run these models. we need advanced computer systems. Data collection may be another limitation of the study. The next studies can develop the TCN model to process information in two directions. In addition, we can use different methods such as the analysis of variance method (ANOVA) to decompose uncertainty values into parameter and input uncertainties.