Abstract
A graphene-loaded metamaterial absorber is investigated in the mid-infrared region. The light-graphene interaction is greatly enhanced by virtue of the coupled resonance through a cross-shaped slot. The absorption peaks show a significant blueshift with increasing Fermi level, enabling a wide range of tunability for the absorber. A simple circuit model well explains and predicts this modulation behavior. Our proposal may find applications in a variety of areas such as switching, sensing, modulating, and biochemical detecting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Plasmonic metamaterial (PM) absorbers work with metallic nanostructures at deep subwavelength scale. Perfect absorptions can be achieved and tailored at particular wavelengths, leading to a variety of applications including light emitter/detector, sensor, photothermal therapy, optical-mechanical interaction, and hyperspectral imaging [1,2,3,4,5,6,7]. PM absorbers also provide a promising platform for designing novel functional devices with tunable properties. By introducing components such as liquid crystals, semiconductors, or phase-change materials, the optical response can be modulated electrically, optically, or thermally [8,9,10,11,12,13], which enables new types of modulators, switches, and multispectral detectors.
Most recently, graphene has received considerable attention because of its high-speed modulation capability and tunability as a plasmonic material [14,15,16,17,18,19,20]. Specifically, the graphene conductivity depends on the Fermi level (EF) which can be continuously tuned through bias voltage within several nanoseconds, enabling a high modulation rate in the near infrared and mid-infrared regions [17, 19,20,21,22,23,24]. However, as the single graphene layer is only atomically thick, the interaction between the incident light and the plasmonic resonance is quite weak. And this interaction becomes even weaker in the mid-infrared area due to the Pauli blocking of interband transitions [22]. As a result, the wavelength tuning range as well as the modulation depth is quite limited. The wavelength shift is generally less than 10% of the resonance wavelength [21, 22, 25,26,27,28], which is still a challenge for practical applications in optical communications and wideband spectral detections. Thus, in order to achieve efficient electro-optical modulation, the graphene-light interaction needs to be greatly strengthened. Some progresses have been made in previous studies. Based on the designs of complex nanostructures such as nano-antennas and split ring resonators [19, 21, 22, 25, 27, 28], the enhancement of graphene-light interaction has been theoretically and experimentally demonstrated. Yet, these designs are usually complicated or polarization-dependent, the range of working frequency is relatively small and the tunability is still limited.
In this work, we have proposed a graphene-loaded absorber with modulation range from 9 to 14 μm, which is of great interest for applications such as biochemical sensing and thermal imaging [5, 29,30,31]. The coupled-resonances inside the cross-shaped slot offer four orders of enhancement for the electric field, strongly intensifying the graphene-light interaction and resulting in a shift of up to 25% in the central wavelength. In addition, we propose a simple LC circuit model which well explains and predicts the graphene-induced modulation controlled by the voltage and geometric parameters. Such a large range of tunability would be promising in many applications.
Methods
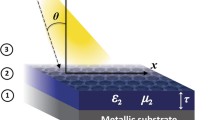
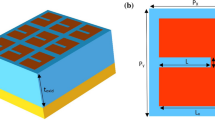
As shown in Fig. 1a, patterned metallic patches are arranged with a period of Λ = 8 μm on the metal substrate separated by a dielectric spacer. A single layer of graphene sandwiches between the patches and the spacer. The substrate is very thick and acts as a reflection mirror. The thickness of the spacer layer is td = 520 nm and that of the metallic patches is tm = 100 nm. Figure 1b shows the top view of one unit cell. Two subunits are arranged in a diagonal symmetry in order to support the polarization independence. A cross-shaped slot is etched on each square patch, dividing it into four small identicals. The sizes of the small identicals in S1 and S2 are l1 = 1.5 μm and l2 = 1.7 μm, respectively. The slot width for both subunits is a = 20 nm. In our study, the metallic material is chosen as gold (Au), whose optical property is described by the Drude model of \( \varepsilon \left(\omega \right)=1-{\omega}_p^2/\left(\omega \left(\omega +\tau \right)\right) \) with ωp = 1.369 × 1016 Hz and τ = 1.224 × 1014 Hz [32]. The dielectric spacer is composed of zinc sulfide (ZnS), whose optical index is n = 2.2 with negligible loss in the mid-infrared region [33].
a Schematic diagram of the proposed graphene-loaded metamaterial. The cross-shaped slot in each subunit enables a great enhancement of graphene-light interaction without polarization dependence. b Top view of the structure in one period. Two subunits are arranged diagonally with different patch sizes
The finite-difference time-domain (FDTD; Lumerical FDTD Solutions) method is employed to calculate reflectance spectra and electromagnetic field distribution. The simulations are carried out with periodic boundary conditions in the x and y directions and perfect matched layer conditions in the z directions. The single graphene layer is modeled as a two-dimensional structure by the surface conductivity approach [34]. The surface conductivity of the graphene layer σg, including the interband term σinter and the intraband term σintra, can be calculated by the Kubo formula [35].
where e and ξ are the charge and energy of the electron, ℏ is the reduced plank’s constant, ω is the angular frequency, \( {f}_d\equiv 1/\left({e}^{\left(\xi -{E}_F\right)/{k}_BT}+1\right) \) refers to the Fermi-Dirac distribution, T is the absolute temperature, Γ is the scattering rate, kB is the Boltzmann constant, and EF is the Fermi level. In our calculation, T = 300 K, and Γ = 10 meV [28]. The mesh size near the graphene layer is 0.25 nm, and 2.5 nm in the slots. The effective permittivity of graphene can then be expressed as
where ε0 is the permittivity of vacuum, and tg is the thickness of graphene layer. Equations (1) and (2) demonstrate that the optical constants of graphene change with EF. This change leads to tunability of the absorption frequency, whose range can be greatly enlarged by the coupled resonance in the nanostructures, substantially lowering the applied voltage in devices.
Results and Discussion
Figure 2a shows the absorption spectra for x-polarized wave (φ = 0) at the normal incidence. When the Fermi level is EF = 0eV, two absorption peaks are observed at the wavelength λ = 12.4 μm and 13.3 μm, respectively. The incident light ranging from 12.1 to 13.5 μm is almost absorbed by the nanostructure. As EF increases, the resonance moves toward shorter wavelength. At EF = 0.2 eV, the absorption peaks shift to 11.8 μm and 12.46 μm, indicating respectively a relative shift of 4.8% and 6%. Meanwhile, the absorbance of peak 2 declines, which is attributed to the impedance mismatch between the metamaterial and air at a higher EF [28]. Here, it is interesting that peak 2 blueshifts faster than peak 1 as the Fermi level keeps increasing. This observed behavior will be explained later by a circuit model.
Absorption spectra at the normal incidence with different EF at φ = 0, showing large blueshift of the peaks with increasing EF (a), and with different φ at EF = 0.2eV, demonstrating a polarization independence (b). The polarization angle φ is defined as in Fig. 1a
The modulation can be quantified by a parameter M = Δλ/λ0, where λ0 is the resonance wavelength at EF = 0 eV and Δλ is the wavelength shift due to the change of EF. Figure 2a shows M1 = 20.1% and M2 = 25.5% for peak 1 and peak 2, respectively, when EF reaches 0.6 eV. The modulation range of resonances is much broader compared with previous works [19, 21, 22, 25,26,27,28]. Such a large modulation at a low EF is highly desirable for many applications. Separate calculations show that the absorption peaks blueshift with decreasing thickness of the spacer (Additional file 1). Thus, we can optimize the thickness to set a suitable start point of modulation. In addition, the optical response of the proposed metamaterial is polarization-independent as shown in Fig. 2b. The absorption spectrum keeps unchanged when the polarization angle φ varies from 0 to 90°, owing to the symmetry of the design.
The mechanism of perfect absorptions is clearly illustrated by the field distributions at the resonances. Because of the well-known metal-insulator-metal (MIM) structure [3, 32, 36,37,38] shown in Fig. 1, localized SPPs are stimulated to form compact magnetic resonances in each patch. Figure 3a and b demonstrate the normalized magnetic field |H|2 in the graphene layer for EF = 0.2 eV at the resonance wavelengths of λ1 = 11.8 μm and λ2 = 12.46 μm, respectively. Since the SPPs are strongly localized, two subunits can work independently. However, due to the narrow width of the splitting slot inside each subunit, the resonances of the four identicals are actually coupled to each other. And this coupling tremendously increases the electric field inside the slot, as shown in Fig. 3c and d. Only the E fields in the y-direction slot are obvious here because the incident light is in the x polarization. The intensity of the E field enhanced by the resonance coupling is four orders of magnitude larger than that of the incident light Einc. In contrast, the most intensified fields used for modulation in previous work are at the patch edges. Figure 3e and f show the sharp comparison of the enhancements between the slots and edges along the white line in Fig. 3c and d, respectively.
Field distributions in the graphene layer at EF = 0.2 eV for the x-polarized light at the normal incidence, showing great enhancement in the slot caused by the coupled-resonances. a, b Normalized magnetic field |H|2 at λ1 = 11.8 μm (a) and λ2 = 12.46 μm (b); c, d The corresponding field distribution of |E/Einc|2; e, f |E/Einc|2 along the white dash-line shown in c and d, respectively. A sharp contrast is seen between the intensity inside the slot and that at the patch edges, giving hints for much wider tuning range than that in previous works
Such field distributions well explain the reason why the modulation is so great in our proposal. Based on a perturbation theory, the graphene-induced shifting of resonance can be evaluated as Δω = − iσg∫S|Es|2dS/W0 [22]. Here, |Es|2is the intensity of the electric field in the graphene layer, W0 is the stored energy, and S denotes the area covered by the graphene. The spectral shift of the resonance (Re(Δω)) is decided by the imaginary part of σg, which is much greater than its real part in the mid-infrared region [22, 28]. As clearly shown in the Fig. 3c–f, the enhancement of electric field inside the narrow slot is more than 10 times of that at the edges. As a result, the integral value is mainly contributed by the greatly enhanced E field in the patch slots, leading to a much bigger shift of the peaks than in previous cases which only possess the enhanced E fields at the metallic edges [21, 22, 25, 27, 28].
According to the field distributions and above discussions, an LC circuit model is proposed to study the tuning behavior. As shown in Fig. 4a, Li and Ci (i = 1, 2) are, respectively, the inductance and capacitance for the patch Si in Fig. 1b. When the slot width a is very big and there is no graphene layer, we can ignore the effects induced by the slots and graphene. Then, Li and Ci can be decided by separate calculations through fitting with the resonant wavelength obtained in absorption spectra [37, 39, 40]. The results are L1 = 0.07 pH and C1 = 350 aF for subunit S1, while L2 = 0.075 pH and C2 = 380 aF for subunit S2. The slot-induced coupling effect inside each subunit can be described by a shunt capacitance Cc, which is found to decrease with the increasing slot width a. In our cases, Cc is 290 aF for a = 20 nm, and becomes 200 aF, 180 aF, and 135 aF with every increasing 10 nm of a. The resonance wavelength is obtained by letting the impedance of the circuit to be zero, i.e., \( {\lambda}_i^0=2\pi {c}_0\sqrt{L_i{\mathrm{C}}_i^0} \). Here, c0 is the light speed in vacuum, “i” refers to subunit Si, and \( {C}_i^0={C}_i+{C}_c \).
a An LC circuit model includes contributions from separate patches (Liand Ci), slot (Cc), and graphene (Lg). b Resonances calculated by the LC model compared with FDTD simulations. c, d Resonance shift for a single patch at EF = 0.4 eV with changing geometrical parameter of c slot width (l = 1.5 μm) and d patch size (a = 20 nm)
The two-dimensional graphene layer basically acts as an inductor. As shown in Fig. 3, the main contribution of the graphene layer comes from the slot position where the electric field is intensified. Since the slot width is much smaller than the operating wavelength and the wavelength of graphene plasmon, the quasi-static approximation is valid. The voltage V and the current I across the slot can be evaluated by V = aE andI = 2litg(σg − iωε0)E, where E is the electric field in the graphene layer. So, we can introduce an inductance Lg = − 1/ω Im(V/I) [41], which describes the contribution of the graphene layer and is found to be
This inductor serves as a parallel element shown in Fig. 4a. As a result, the total inductance of one patch is obtained by \( 1/{L}_i^{\prime }=1/{L}_i+1/{L}_{\mathrm{g}} \). The final resonance wavelength of each subunit, with the graphene layer, becomes
Because each subunit works independently, the total impedance of the metamaterial can be obtained from the parallel connection of the impedances of the two subunits.
This LC model predicts a blueshift of the resonance with increasing EF. Deduced from Eqs. (1) and (2), we get a larger value of |Re(εg)| for the graphene at a higher EF, which gives a smaller Lg in Eq. (3). Because of the parallel connection of the inductors, the final inductor \( {L}_i^{\prime } \) becomes smaller, leading to a shorter wavelength of resonance in Eq. (4). The calculated result is summarized in Fig. 4b, showing a good agreement with the resonant wavelength obtained by the FDTD simulations. Small deviation is seen because our LC model ignores the contribution of weak fields at the edges of each patch (Fig. 3c–f). The LC model also shows how the geometric parameters influence the blueshift of the resonance. Differentiating Eq. (4), we have \( \partial {\lambda}_i^{\prime }/\partial {L}_i^{\prime}\propto 1/\sqrt{L_i^{\prime }} \). It is obvious that a small value of \( \sqrt{L_i^{\prime }} \) is favored to increase the sensitivity of this blueshift. Because the inductors are parallelly connected and Li is fixed, a small value of the total inductance \( {L}_i^{\prime } \) means a small value of the graphene inductance Lg. In order to increase the tuning range, the slot width a should be small and the patch size l be large, according to Eq. (3). Figure 4c shows that the blueshift of resonance at EF = 0.4 eV increases from around 6 to 15%, when the slot width inside S1 decreases from 50 to 20 nm. On the other hand, if we fix the slot width at a = 20 nm, the resonance increases from 15 to 22% with patch size changing from 1.5 to 1.8 μm as shown in Fig. 4d. The good agreement with the FDTD simulations demonstrates that such a simple circuit model is an efficient method for studying related metamaterials devices.
Conclusions
In conclusion, we have designed a polarization-independent, broadband metamaterial absorber with a large range of modulation. For both resonances, the tuning range reach up to 20.1% and 25.5% of the central wavelength when EF increases from 0 to 0.6 eV. Such a large modulation comes from the graphene-light interaction tremendously enhanced by the coupled-resonances inside the cross-shaped slot of each metallic patch. This effect is well described by a graphene-introduced inductor in the LC model. Such a simple model predicts the modulation behavior under different geometric parameters, and the results agree well with the FDTD simulations. Our proposal is beneficial to potential applications such as optical communication, sensing, and thermal imaging.
Abbreviations
- E F :
-
Fermi level
- FDTD:
-
Finite-different time-domain
- MIM:
-
Metal-insulator-metal
- PM:
-
Plasmonic metamaterial
- ZnS:
-
Zinc sulfide
References
Zhu H, Yi F, Cubukcu E (2016) Plasmonic metamaterial absorber for broadband manipulation of mechanical resonances. Nat Photonics 10(11):709
Ndukaife JC, Shalaev VM, Boltasseva A (2016) Plasmonics—turning loss into gain. Science 351:334–335
Xie Q, Dong G, Wang B-X, Huang W-Q (2018) Design of quad-band terahertz metamaterial absorber using a perforated rectangular resonator for sensing applications. Nanoscale Res Lett 13:137
Wang H, Chen Q, Wen L, Song S, Hu X et al (2015) Titanium-nitride-based integrated plasmonic absorber/emitter for solar thermophotovoltaic application. Photonics Research 3:329–334
Tittl A, Michel AKU, Schäferling M, Yin X, Gholipour B et al (2015) A switchable mid-infrared plasmonic perfect absorber with multispectral thermal imaging capability. Adv Mater 27:4597–4603
Li H, Qin M, Wang L, Zhai X, Ren R et al (2017) Total absorption of light in monolayer transition-metal dichalcogenides by critical coupling. Opt Express 25:31612–31621
Li H, Ren Y, Hu J, Qin M, Wang L (2018) Wavelength-selective Wide-angle Light Absorption Enhancement in Monolayers of Transition-Metal Dichalcogenides. J Lightwave Technol. 36(16):3236–3241
Yang A, Yang K, Yu H, Tan X, Li J et al (2016) Piezoelectric tuning of narrowband perfect plasmonic absorbers via an optomechanic cavity. Opt Lett 41:2803–2806
Carrillo SG-C, Nash GR, Hayat H, Cryan MJ, Klemm M et al (2016) Design of practicable phase-change metadevices for near-infrared absorber and modulator applications. Opt Express 24:13563–13573
Zhu Z, Evans PG, Haglund RF Jr, Valentine JG (2017) Dynamically reconfigurable metadevice employing nanostructured phase-change materials. Nano Lett 17:4881–4885
Song Z, Wang Z, Wei M (2019) Broadband tunable absorber for terahertz waves based on isotropic silicon metasurfaces. Mater Lett 234:138–141
Song Z, Wang K, Li J, Liu QH (2018) Broadband tunable terahertz absorber based on vanadium dioxide metamaterials. Opt Express 26:7148–7154
Chu Q, Song Z, Liu QH (2018) Omnidirectional tunable terahertz analog of electromagnetically induced transparency realized by isotropic vanadium dioxide metasurfaces. Appl Phys Express 11:082203
Guo Z, Nie X, Shen F, Zhou H, Zhou Q et al (2018) Actively tunable terahertz switches based on subwavelength graphene waveguide. Nanomaterials 8:665
Luo L, Wang K, Ge C, Guo K, Shen F et al (2017) Actively controllable terahertz switches with graphene-based nongroove gratings. Photonics Research 5:604–611
Emani NK, Chung T-F, Kildishev AV, Shalaev VM, Chen YP et al (2013) Electrical modulation of Fano resonance in plasmonic nanostructures using graphene. Nano Lett 14:78–82
He X, Zhao Z-Y, Shi W (2015) Graphene-supported tunable near-IR metamaterials. Opt Lett 40:178–181
Yu R, Pruneri V, García de Abajo FJ (2015) Resonant visible light modulation with graphene. ACS Photonics 2:550–558
Zeng B, Huang Z, Singh A, Yao Y, Azad AK et al (2018) Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and single-pixel imaging. Light Sci Appl 7:51
Li H, Wang L, Liu J, Huang Z, Sun B et al (2013) Investigation of the graphene based planar plasmonic filters. Appl Phys Lett 103:211104
Yao Y, Kats MA, Shankar R, Song Y, Kong J et al (2014) Wide wavelength tuning of optical antennas on graphene with nanosecond response time. Nano Lett 14:214–219
Dabidian N, Kholmanov I, Khanikaev AB, Tatar K, Trendafilov S et al (2015) Electrical switching of infrared light using graphene integration with plasmonic Fano resonant metasurfaces. ACS Photonics 2:216–227
Chen Y, Yao J, Song Z, Ye L, Cai G et al (2016) Independent tuning of double plasmonic waves in a free-standing graphene-spacer-grating-spacer-graphene hybrid slab. Opt Express 24:16961–16972
Li H, Ji C, Ren Y, Hu J, Qin M et al (2019) Investigation of multiband plasmonic metamaterial perfect absorbers based on graphene ribbons by the phase-coupled method. Carbon 141:481–487
Mousavi SH, Kholmanov I, Alici KB, Purtseladze D, Arju N et al (2013) Inductive tuning of Fano-resonant metasurfaces using plasmonic response of graphene in the mid-infrared. Nano Lett 13:1111–1117
Liao Y-L, Zhao Y (2017) Graphene-based tunable ultra-narrowband mid-infrared TE-polarization absorber. Opt Express 25:32080–32089
Zhang YP, Li TT, Chen Q, Zhang HY, O'Hara JF et al (2015) Independently tunable dual-band perfect absorber based on graphene at mid-infrared frequencies. Sci Rep 5:18463
Vasić B, Gajić R (2013) Graphene induced spectral tuning of metamaterial absorbers at mid-infrared frequencies. Appl Phys Lett 103:261111
Rodrigo D, Limaj O, Janner D, Etezadi D, De Abajo FJG et al (2015) Mid-infrared plasmonic biosensing with graphene. Science 349:165–168
Vollmer M, Mollmann, KP (2010) Infrared Thermal Imaging|Fundamentals, Research and Applications. Wiley-VCH, Weinheim
Guo Q, Yu R, Li C, Yuan S, Deng B, et al. (2018) Efficient electrical detection of mid-infrared graphene plasmons at room temperature. Nat Mater 17:986–992
Liu N, Mesch M, Weiss T, Hentschel M, Giessen H (2010) Infrared perfect absorber and its application As plasmonic sensor. Nano Lett 10:2342–2348
Palik ED (1985) Handbook of optical constants of solids. Academic Press, New York
Hanson GW (2008) Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J Appl Phys 103:064302
Gusynin V, Sharapov S, Carbotte JP (2006) Magneto-optical conductivity in graphene. J Phys-Condens Mat 19(2):026222
Wu D, Li R, Liu Y, Yu Z, Yu L et al (2017) Ultra-narrow band perfect absorber and its application as plasmonic sensor in the visible region. Nanoscale Res Lett 12:427
Xiao D, Tao K, Wang Q (2016) Ultrabroadband mid-infrared light absorption based on a multi-cavity plasmonic metamaterial array. Plasmonics 11:389–394
Xiao D, Tao K (2015) Ultra-compact metamaterial absorber for multiband light absorption at mid-infrared frequencies. Appl Phys Express 8:102001
Matsuno Y, Sakurai A (2017) Perfect infrared absorber and emitter based on a large-area metasurface. Optical Materials Express 7:618–626
Tassin P, Koschny T, Kafesaki M, Soukoulis CM (2012) A comparison of graphene, superconductors and metals as conductors for metamaterials and plasmonics. Nat Photonics 6:259
Yao Y, Kats MA, Genevet P, Yu N, Song Y et al (2013) Broad electrical tuning of graphene-loaded plasmonic antennas. Nano Lett 13:1257–1264
Acknowledgements
Not applicable.
Funding
This work was supported by the Chinese Natural Science Foundation (Grant Nos. 61107049, 11734012), Basic Research Program of Shenzhen (JCYJ20170302151033006), Natural Science Foundation of Guangdong Province (2017A030310131).
Availability of Data and Materials
All date can be provided on a suitable request.
Author information
Authors and Affiliations
Contributions
DX conducted the simulations and processed the data and figures. All authors participated in discussions. KYT, DX, ZBOY, QL, and LL prepared the manuscript. KYT supervised the whole work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Additional file
Additional file 1:
Supplementary Material. (PDF 308 kb).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Xiao, D., Liu, Q., Lei, L. et al. Coupled Resonance Enhanced Modulation for a Graphene-Loaded Metamaterial Absorber. Nanoscale Res Lett 14, 32 (2019). https://doi.org/10.1186/s11671-019-2852-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-019-2852-y