Abstract
The paper considers the influence of aging of high-temperature phase on subsequent martensitic transformation in Cu-Al-Mn alloy. The morphology of behavior of martensitic transformation as a result of alloy aging under annealing in a constant magnetic field with different sample orientation relatively to the field direction and without field was studied for direct control of the processes of martensite induction at cooling. Temperature dependences of electrical resistance, magnetic susceptibility, and magnetization, as well as field dependences of magnetization, and phase composition were found. The tendency to the oriented growth of precipitated ferromagnetic phase nanoparticles in a direction of applied field and to an increase of their volume fraction under thermal magnetic treatment of material that favors a reversibility of induced martensitic transformation is observed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Phase transformations of martensitic type are inherent to a wide class of materials and alloys, which are characterized by structural features that determine peculiarities of their formation and physical properties. Priority in research of new materials belongs to alloys, in which the structural phase transformations of martensitic-type are realized in a ferromagnetic matrix, such as Heusler alloys, intermetallic compounds Co-Ni-Al, Co-Ni-Ga alloys, and Fe-based alloys.
A mechanism of the behavior of martensitic transformation (MT), occurring in alloy after decomposition of solid solutions with precipitation of ferromagnetic nanoparticles in the nonferromagnetic matrix, is not less attractive. Such behavior is typical for Cu-Co, Cu-Ni-Fe, Cu-Ni-Co, and Ni-Mn alloys. In ternary Cu-Al-Mn Heusler alloy, MT can take place [1] and an appearance of long-range ferromagnetic order in a system of superparamagnetic nanoparticles, dissolved in the nonmagnetic matrix, is caused by the cooperative ordering of their magnetic moments. Alloys of this system demonstrate high values of characteristics of shape memory effects and superelasticity [2–4]; they also exhibit a giant magnetoresistance [5].
As it has been established by neutron diffraction measurements [6] that only the Mn atoms possess a magnetic moment, Winkler et al. [7] have shown that the chemical order determines the magnetic behavior of the alloys because it establishes the distances between Mn atom pairs. The Mn-Mn interactions can be ferromagnetic as in Cu2MnAl or antiferromagnetic as in MnO, or a mixture of both as in Cu-Mn alloys [6], depending on the magnetic moment of each atom and the distances between them. Only 35 % of Mn atoms are involved in the ferromagnetic Cu2MnAl phase formation while others are dissolved in the nonmagnetic matrix [8].
The stoichiometric compound CuAlMn is ferromagnetic with a Curie temperature of 630 K, and it is known that the entire magnetic moment of the system must be attributed to the Mn atoms [9] coupled via the Ruderman-Kittel-Kasuya-Yosida interaction [10]. After a suitable heat treatment [11], the Cu3−x AlMn x (x < 1) alloys display an L21 structure (Fm3m space group) that can be viewed as defined on a bcc lattice divided into four interpenetrated fcc sublattices.
The high-tempetarure β1-phase of binary and ternary copper-aluminum alloys has an ordered bcc structure of DO3 type [12]. The miscibility gap is found below the L21 ordering line in Cu-Al-Mn systems. Phase separation between nonmagnetic DO3(Cu3Al)-rich and ferromagnetic L21(Cu2AlMn)-rich domains takes place in this region [13].
Martensitic phases, formed in alloys of various compositions, are closely-packed structures, which differ by the order of stacking of closely-packed planes: β1′(3R) or γ′(2H) [12]. The martensite crystals inherit coherent particles from austenite, the crystal lattice of which varies due to an elastic deformation that is caused by changing conditions of lattice conjugation of nanoparticles and a matrix at MT.
Annealing in the β phase produces changes in the martensitic transformation temperature. These changes have been shown to be associated with order-disorder process at low temperature [14] or precipitation of equilibrium phases at higher temperatures [15].
Thus, by varying regimes of aging of high-temperature phase (austenite), it is possible to considerably affect the process of its decomposition [16] that can result in significant changes of characteristic temperatures and a hysteresis of MT in Cu-Al-Mn alloys. By following certain conditions in aging process, it is possible to achieve a situation that results in an increase of MT start temperature (M s) and a decrease of MT temperature hysteresis (ΔT = A f − M s, where A f is a final temperature of inverse transition, M s is a start temperature of direct transformation). The first condition is related to β1–matrix depletion with manganese, and the second one is associated with a decrease in the shear strain of transformation area due to a reduction of elastic energy (E el) on phase interface. A certain heat treatment allows controlling a number and a size of particles in the alloy, and MT characteristic temperature and hysteresis value substantially depend on the size and amount of particles [16]. Recent studies [17, 18] have shown that Cu-Mn-Al alloys with a high content of Mn have acceptable mechanical properties that open the possibilities of their practical application.
To develop a concept of the nature and character of MT behavior and to directly control the process of MT induction, it is of great interest to study the morphology of MT behavior in Cu-Al-Mn alloy after an aging of high-temperature phase as a result of annealing in a constant magnetic field depending on sample orientation relative to the field. For this purpose, in order to select the best regime of thermal or thermal-magnetic treatment, the Cu-Al-Mn alloy with a chemical composition which provides the lowest value of MT temperature hysteresis was chosen for the investigations.
Methods
The Cu-Al-Mn alloy was smelted in an induction furnace in an argon atmosphere. According to energy dispersive X-ray fluorescent analysis data, the chemical composition of the alloy is as follows (in mass %): Cu (84.7), Al (11.1), and Mn (4.2) with error in margin ±0.5 %.
After homogenizing annealing at 1123 K for 10 h, the samples were quenched in water and then were annealed at a constant temperature of 498 K for 3 h. The permanent magnetic field with a strength of 1.5 kOe was created by the selection of ferromagnetic plates which were spaced by a distance, required for a placement of an electrical heater with a sample in their gap. The placement of samples in relation to a direction of magnetic field and without it is shown in Fig. 1. To eliminate the influence of magnetic field of the electrical heater on a sample, the bifilar nichrome wire winding was used. The samples had a working length of 20 mm with a cross section of 2 × 2 mm2.
Scheme of placement of Cu-Al-Mn alloy samples at annealing: a without a field; b in the magnetic field perpendicular to the main axis of sample; and c in the magnetic field parallel to the main axis of sample, where 1 is an electrical heater, 2 is a sample, 3 is a thermocouple, and 4 is а magnetic pole
Characteristic temperatures and MT hysteresis were determined from the curves of temperature dependences of electrical resistance (ρ/ρ mах) and magnetic susceptibility (χ/χ mах) according to a standard technique. Temperature and field dependences of magnetization were also a subject of study. Phase composition of samples was defined using X-ray diffractometer Rigaku Ultima IV in monochromatic Кα-radiation of Cu-anode.
Results and discussion
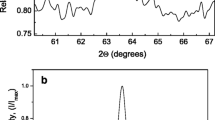
The results of X-ray phase analysis (Fig. 2a) testify the β1-phase (of close to Cu3Al composition) formation after the cooling (with use quenching in water) as a result of ordering (β → β1) of high-temperature (austenitic) β-phase. The subsequent annealing leads to the Cu-Al-Mn alloy aging accompanying by precipitation of dispersed particles of ferromagnetic β3-phase of Cu2AlMn composition in β1-matrix [15, 16].
After annealing without magnetic field (Fig. 2b), there are no reflections observed from β3-phase on diffraction patterns that can be explained by a low percentage of this phase in the alloy or/and its high dispersed (nanosized) state.
The annealing in the magnetic field (Fig. 2c, d) favors the precipitation of β3-phase (Cu2AlMn) particles in β1-matrix, as argued by an appearance of reflections of weak intensity from β3-phase at appropriate angles. The weak intensity of reflections can indicate that the particles of precipitated phase are nanosized. Change in sample orientation relative to the magnetic field direction during the aging affects β3-phase formation. After annealing in the parallel field, the diffraction lines from β3-phase are slightly more intense than after annealing in the perpendicular field that can testify about more amount of this phase in the alloy.
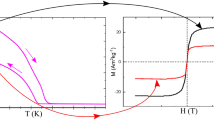
The character of the temperature dependence of electrical resistance is the same like in metal alloys (Fig. 3). At the temperature of MT start (M s), the growth of electrical resistance of samples, associated with the replacement of a volume fraction of initial phase by the phase which has a more defect structure, occurs. As it is evident from Fig. 3, further heating of samples after MT has a reversible character with the inverse sequence of reproduction.
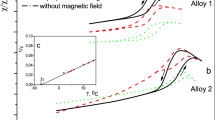
According to the results of measurements of low-field magnetic susceptibility (χ/χ mах) of Cu-Al-Mn alloy at different regimes of aging (see Fig. 4), there is a slight increase in the start temperature (M s) of direct β1↔β′ transformation after annealing in magnetic field and a decrease in the width of MT temperature hysteresis (ΔT). The increase in Ms, in this case, is caused by depletion of β1-matrix with manganese. A lower amplitude of a transition jump on the χ/χ mах curves for samples with thermomagnetic treatment is associated with a dominant orientation of nanoparticles which are allocated in a direction of applied external magnetic field. In the case of thermal treatment without a magnetic field, the spherical concentration inhomogeneities are distributed in a sample, mainly, chaotically, in contrast to thermomagnetic treatment, which orders the Cu2MnAl phase nanoparticles nucleation.
Such effect of thermal magnetic treatment on magnetic susceptibility can be explained by the fact that magnetic characteristics of the investigated alloy are defined by an interaction of nanoparticles of precipitated phase. Nanoparticles that are within the martensite crystals are subjected to considerable coherent stresses caused by a crystal lattices mismatch of martensite and nanoparticles, which leads to magnetic anisotropy of nanoparticles ensemble. The crystal lattice mismatch sharply increases when cubic lattice of the austenitic matrix is transformed into the orthorhombic lattice of martensite, and, thus, the temperature dependence of magnetic susceptibility is caused by a corresponding change in magnetic anisotropy of nanoparticles.
As it is known from the phenomenological theory of diffusion decay [19], the change in free energy of the system is represented as three components, which are determined by the change in volume, surface, and elastic energies:
When the magnetic field is applied during the alloy aging, the phase, which forms, can have a superparamagnetic state [20], and, in this case, a component, responsible for an interaction of magnetization of phase with the external magnetic field (ΔG m), is added to the expression for free energy of system that leads to the equation correction:
The radius of a critical nucleus of a new phase, which can be defined using a standard procedure of free energy minimization relative to the radius of new phase nucleus, is as follows [21]:
where γ s is a surface energy of the system, g v is a specific change in thermodynamic potential of precipitated phase relative to the matrix, е v is a specific elastic energy, I is a magnetization of a new phase, and B is an induction of magnetic field. So, the energy of formation of a new phase critical nucleus, in turn, can be expressed by a formula [21]:
It should be noted that in the case of applying an external magnetic field, the critical nucleus size and the energy of its formation decreases. At a certain temperature and aging time, the application of magnetic field stimulates the formation of new nuclei, which agrees well with the behavior of magnetization (Figs. 5 and 6), which, in turn, depends on the amount of precipitated ferromagnetic nanoparticles. A magnetic moment of alloy depends on, as it is known, the magnetic moment of manganese atoms, and the distance between them as well [6].
The field dependences of magnetization of Cu-Al-Mn alloy samples after aging at different regimes: (1) without a magnetic field; (2) in the perpendicular magnetic field; (3) in the parallel magnetic field; a in martensite state (−40 °C); and b in austenite state (+40 °C); where σ s is a saturation magnetization
According to the Boltzmann distribution, the magnetization of an ensemble of non-interacting ferromagnetic nanoparticles is defined by a relation [20, 22]:
where L is the Langevin function equal to:
where m is a magnetic moment of the nanoparticle, n is a number of nanoparticles per unit volume, and k is the Boltzmann constant.
By applying an external magnetic field, the particles growth in the direction of field takes place due to the minimization of magnetostatic and surface energies of particles resulting in a system free energy decrease. When choosing an effective temperature interval of thermal magnetic treatment (TMT) for aging, it was taken into account the fact that the interfacial energy and magnetization possess low values near a decay curve on a diagram of states [23], so, the TMT for the formation of anisotropic ferromagnetic nanoparticles was carried out in region of these temperatures (at 225 °C).
As it follows from Figs. 4, 5 and 6 a number of precipitated nanoparticles are maximal in the case of annealing in the parallel magnetic field. In turn, an increase in a number of precipitated nanoparticles stimulates the growth of start temperature of direct MT and the reduction of MT hysteresis. The transformation hysteresis is small, thus, an accurate determination of the equilibrium temperature T 0 between the β and martensitic phase as T 0 ≈ (M s + A f)/2 becomes possible [24].
Reducing the MT temperature hysteresis (ΔТ), in this case, agrees well with results of [16]:
where T 0 is the temperature of equilibrium between austenitic and martensitic phases, L is the MT heat, and α is a coefficient which depends on strength characteristics of the material and determines the degree of coherent stress relaxation.
A low cold deformation reduces the magnitude of the elastic modulus of solid solutions (as well as pure metals). At high degrees of deformation, it is possible to increase it due to the formation of texture. The presence of magnetostriction phenomenon (connected with a change in linear size at magnetic ordering) in ferromagnetics leads to the fact that they have a lower modulus of elasticity: E ferr = E norm − E. The increase of volume fraction of precipitated phase nanoparticles leads to decrease in a strain of the transformation, and, as a result, to the reduction of the system elastic energy (E el), what stimulates the reducing the MT temperature hysteresis [16].
Conclusions
The paper was attempted to the process control of phase formation at the aging of high-temperature phase using a constant magnetic field with the strength of 1.5 kOe in order to optimize the parameters of martensite transformation behavior in Cu-Al-Mn alloy. With the help of the phenomenological theory of diffusion decay and obtained experimental results, the behavior of induced MT in Cu-Al-Mn alloy was explained and its causes were found out. One can assume that applying a magnetic field stimulates the formation of ferromagnetic nanoparticles during the decay of solid solution. In addition, thermomagnetic treatment helps to create effective nucleation centers of nanoparticles in Cu-Al-Mn alloy during the aging of high-temperature phase.
Thus, annealing in a magnetic field promotes the increasing of ferromagnetic nanoparticles number in the nonferromagnetic matrix, as evidenced by measuring the magnetic properties of the material sample, such as field dependences of magnetization and low-field magnetic susceptibility.
For the further and in-depth understanding of decay processes impact on the behavior of martensitic transformation, it is planned to continue the work in the direction of the study of microstructural features of phase formation by applying direct methods.
Abbreviations
- MT:
-
martensitic transformation
- TMT:
-
thermal magnetic treatment
References
Warlimont H, Delay L (1974) Martensitic transformations in copper-, silver-, and gold-based alloys. Pergamon, Oxford
Kainuma R, Takahashi S, Ishida K (1996) Thermoelastic martensite and shape memory effect in ductile Cu-Al-Mn alloys. Metall Mater Trans A 27(8):2187–2195
Kainuma R, Takahashi S, Ishida K (1995) Alloys of the Cu-Al-Mn system. J Phys IV France C8:961–966
Kozlova LE, Titenko AN (2006) Stress-induced martensitic transformation in polycrystalline aged Cu-Al-Mn alloys. Mater Sci Eng A 438–440:738–742. doi:10.1016/j.msea.2006.02.159
Sugimoto S, Kondo S, Nakamura H, Book D, Wang Y, Kagotani T, Kainuma R, Ishida K, Okada M, Homma M (1998) Giant magnetoresistance of Cu3Al–Cu2MnAl melt-spun ribbons. J Alloys Compd 265(1):273–280. doi:10.1016/S0925-8388(97)00303-4
Prado MO, Lovey FC, Cival L (1998) Magnetic properties of Cu-Mn-Al alloys with shape memory effect. Acta Mater 46(1):137–147
Winkler R, Wachtel E (1978) Magnetic properties and atomic ordering of Mn0.25-Cu-Al alloys. J Magn Magn Mater 9(1-3):270–272. doi:10.1016/0304-8853(78)90068-9
Takzey GA, Mirebeau I, Gun'ko LP, Sych II, Surzhenko OB, Cherepov SV, Troschenkov YN (1999) Study of the onset of a long-range ferromagnetic order in an ensemble of small particles with giant magnetic moments. J Magn Magn Mat 202(2):376–384. doi:10.1016/S0304-8853(99)00357-1
Webster PJ, Ziebeck KRA (1988) Heusler alloys. In: Wijn HPJ (ed) Landolt-Börnstein—group III condensed matter 19c (alloys and compounds of d-Elements with main group elements. Part 2). Springer, Berlin, p 75. doi:10.1007/10353201_12
Tajima K, Ishikawa Y, Webster PJ, Stringfellow MW, Tochetti D, Ziebeck KRA (1977) Spin waves in a Heusler alloy Cu2MnAl. J Phys Soc Jpn 43:483–489. doi: 10.1143/JPSJ.43.483
Obrado E, Frontera C, Manosa L, Planes A (1998) Order-disroder transtions of Cu-Al-Mn shape-memory alloys. PhysRev B 58:14245. doi:10.1103/PhysRevB.58.14245
Delaey L (1991) Diffusionless transformations. In: Cahn RW, Haasen P, Kramer EJ (eds) Materials Science and Technology: A Comprehensive Treatment, vol 5: Phase transformations in materials. VCH, Weinheim, pp 339–404
Bouchard M, Thomas G (1975) Phase transitions and modulated structures in ordered (Cu-Mn)3Al alloys. Acta Metall 23(12):1485–1500. doi:10.1016/0001-6160(75)90159-5
Prado MO (1998) The influence of β phase aging on the martensitic transformation temperatures of CuMnAl alloys. Scripta Metall Mater 38(3):375–383. doi:10.1016/S1359-6462(97)00473-9
Kenichi M, Takashi O, Taira O (1985) Effects of manganese and ageing on martensitic transformation of Cu-Al-Mn alloys. J Mater Sci 20(2):689–699. doi:10.1007/BF01026544
Kokorin VV, Kozlova LE, Titenko AN (2002) Temperature hysteresis of martensite transformation in aging Cu–Mn–Al alloy. Scripta Mat 47(8):499–502. doi:10.1016/S1359-6462(02)00136-7
Sutou Y, Omori T, Wang JJ, Kainuma R, Ishida K (2004) Characteristics of Cu–Al–Mn-based shape memory alloys and their applications. Mater Sci Eng A 378(1):278–282. doi:10.1016/j.msea.2003.12.048
Sutou Y, Omori T, Kainuma R, Ishida K (2003) Effect of grain size and texture on superelasticity of Cu-AI-Mn-based shape memory alloys. J Phys IV France 112:511–514. doi:10.1051/jp4:2003936
Zhdanov GS, Khundzhua AG (1988) Lection on solid state physics. Izd. MGU, Moscow (in Russian)
Kokorin VV (1987) Martensitic transformations in inhomogeneous solid solution. Naukova Dumka, Kiev, p 166, in Russian
Osinskaya Yu V, Petrov SS, Pokoev AV, Radzhabov AK, Runov VV (2012) Kinetics of aging of the Cu-Be alloy with different beryllium concentrations in an external constant magnetic field. Phys Solid State 54(3):568–572. doi:10.1134/S1063783412030249
Vonsovskiy SV (1971) Magnetism. Nauka, Moscow, p 1032 (in Russian)
Chachaturyan AG (1983) Theory of structural transformations in solids. Wiley, New York
Prado M, Lovey FC, Decorte P (1995) Martensitic transformation in Cu-Mn-Al alloys. Scripta Metall Mater 33(6):877–883
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing Interests
The authors declare that they have no competing interests.
Authors’ Contributions
The idea of the study was conceived by AT. AT and LD did the experiments. LD carried out the X-ray analysis. AT measured the electrical and magnetic properties. AT and LD interpreted the experiments and wrote this manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Titenko, A., Demchenko, L. Effect of Annealing in Magnetic Field on Ferromagnetic Nanoparticle Formation in Cu-Al-Mn Alloy with Induced Martensite Transformation. Nanoscale Res Lett 11, 237 (2016). https://doi.org/10.1186/s11671-016-1453-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-016-1453-2