Abstract
The dissociation of zinc ions (Zn2+) from vapor-phase zinc acetylacetonate, Zn(C5H7O2)2, or Zn(acac)2 and its adsorption onto graphene oxide via atomic layer deposition (ALD) were studied using a quantum mechanics approach. Density functional theory (DFT) was used to obtain an approximate solution to the Schrödinger equation. The graphene oxide cluster model was used to represent the surface of the graphene film after pre-oxidation. In this study, the geometries of reactants, transition states, and products were optimized using the B3LYB/6-31G** level of theory or higher. Furthermore, the relative energies of the various intermediates and products in the gas-phase radical mechanism were calculated at the B3LYP/6-311++G** and MP2/6-311 + G(2df,2p) levels of theory. Additionally, a molecular orbital (MO) analysis was performed for the products of the decomposition of the Zn(acac)2 complex to investigate the dissociation of Zn2+ and the subsequent adsorption of H atoms on the C5H7O2 cluster to form acetylacetonate enol. The reaction energies were calculated, and the reaction mechanism was accordingly proposed. A simulation of infrared (IR) properties was performed using the same approach to support the proposed mechanism via a complete explanation of bond forming and breaking during each reaction step.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Two-dimensional (2D) sheets of sp 2-hybridized carbons known as graphene have attracted considerable attention because of their exceptional optical, electrical, chemical, and mechanical properties that impart graphene with the promising ability to develop next-generation functional nanomaterials for various applications [1–3]. To tailor graphene to targeted applications, considerable efforts have been made to control and modify the properties of graphene through various functionalization routes [4]. Furthermore, many studies have been conducted to develop semiconducting material/graphene hybrid structures using either vapor-phase [5–7] or liquid-phase techniques [8–11]. In the past few decades, zinc oxide (ZnO) nanostructures have been considered in many works for optoelectronic and photovoltaic device applications [9–11]. Recently, ZnO/graphene hybrid nanostructure was reported to have excellent potential for use in transparent flexible electrical and optical devices, including flexible photovoltaics, displays, and light emitters [10–15]. The vapor-phase deposition of ZnO using β-diketonates such as acetylacetonate as the Zn precursor was reported as a promising route to grow ZnO nanostructures [12, 14]. Most studies on ZnO/graphene hybrid structures have focused on their structural morphologies and electronic properties [8, 16], whereas few have paid attention to the reaction mechanisms of the semiconducting species at reaction sites on the graphene surface [17, 18]. To our knowledge, no study has reported the reaction mechanism for the vapor-phase deposition of ZnO on graphene utilizing acetylacetonate as a Zn source. In this article, we report the possible reaction mechanism for the deposition of ZnO on pre-oxidized graphene via the injection of vaporized zinc acetylacetonate in the presence of hydrogen.
Methods
Until the early 1990s, quantum chemists used the ab initio Hartree–Fock (HF) approach along with second-order Møller-Plesset perturbation theory as starting points to solve Schrödinger’s equation [19]. Further calculations based on experimental data were carried out for the sake of accuracy through quadratic configuration interaction or coupled cluster theory in the case of small molecules [19, 20]. It is only possible to solve the Schrödinger equation for a one-electron system. Thus, in the late 1980s, density functional theory (DFT) coupled with local density corrected approximation (LDA) was developed as an alternative approximation method to derive reliable solutions to the Schrödinger equation for many-electron systems. In computational physics and chemistry, the HF method is one of the approximation methods that is used to determine the wave function and energy of a quantum many-body system in a stationary state. However, according to the HF approximation, electrons move independently, meaning that both the electron–electron repulsion energy and their total energy are overestimated [20, 21]. The limiting HF energy is therefore higher than the experimental energy. The electron correlation energy is the term used to describe the coupling or correlation of electron motions and is defined as the difference between the HF energy and the experimental energy [20, 22, 23].
To overcome the limitation of the HF approximation, Becke reported a work on density functional thermochemistry in 1993 in which he used DFT coupled with gradient-corrected exchange functional (B88) in conjunction with the Lee-Yang-Parr gradient-corrected correlation functionals (LYP) [19, 24]. Later on, Becke introduced the Becke three-parameter Lee-Yang-Parr (B3LYP) hybrid approach that can overcome the HF approximation limits [19, 24–26]. The B3LYP approach is based on the so-called free electron gas and can be described as a box of non-interacting electrons. This hybrid approach was used to construct the density functional approximations in the present study. Its solution leads to a functional form for a term that accounts for electron correlation. This term, which depends on electron density as well as the gradient of the density presented in Eq. (1), is thus added to the HF Hamiltonian:
where E x GGA and E c GGA are the generalized gradient approximations, and a0, a z , and a c are correlation constants equal to 0.20, 0.72, and 0.81, respectively [19, 27, 28]. This procedure is referred to as a density functional model. Contrary to popular belief, B3LYP was not fitted to experimental data. The three parameters defining B3LYP have been taken without modification from Becke’s original fitting of the analogous B3PW91 functional to a set of atomization energies, ionization potentials, proton affinities, and total atomic energies [28, 29].
Computational Details
The Spartan 14 quantum chemistry package (Wavefunction, USA) was used to perform all calculations in this study [30]. Equilibrium geometries were optimized by the B3LYP density functional method using the 6-311G** basis set; the developer of Spartan chose the Gaussian exponents for polarization functions to give the lowest energies for the modeled molecules. The polarization of the s orbitals on hydrogen atoms is crucial to accurately describe the bonding in acetylacetonate systems, particularly the hydrogen bonding. Furthermore, the 6-31G** basis set provides the p-type polarization functions for hydrogen. This can improve the total energy of the system along with the results for systems with large anions and can impose more flexibility [31]. Zn-containing structures were also optimized with larger basis sets and higher levels of theory [31].
All thermal correction energies were calculated using the 6-311G**, 6-311++G**, and 6-311++G(2df,2pd) (for Zn-containing reactions) basis sets. Calculations involving anions and absolute acidity (e.g., dipole moment calculations) require extra care when selecting the basis sets because extra electrons are weakly coupled to specific atoms or groups of atoms. Thus, the basis sets should provide diffuse s- and p-type functions on non-hydrogen atoms. This is usually designated by the “+” sign, as in 6-311++G**. The second “+” sign indicates that a diffuse function is added to hydrogen [32, 33]. To obtain more accurate energy calculations, single-point calculations were performed at the B3LYP/ 6-311G** optimized geometry using the B3LYP/6-311 + G**, MP2/6-311 + G**, B3LYP/6-311 + G(2df,2p), and MP2/6-311 + G(2df,2p) levels of theory.
Results and Discussion
Dissociation of Zn2+ from the Zn(acac)2 Complex
In this study, the geometries of reactants, transition states, and products were optimized at the B3LYP/6-31G** level of theory or higher. The optimized geometries of transition states, intermediates, and products during the dissociation reaction of Zn2+ from the Zn(acac)2 complex are depicted in Fig. 1. Figure 1a, b shows that rotation and stretching occurred in all the Zn–O bonds of the Zn(acac)2 complex upon the introduction of H atoms. The angle between Zn–O bonds in each of the chelates of the complex increased dramatically from 63.00° to 95.66°, indicating the adsorption of the H atoms towards the center of the complex. Figure 1c shows that both the torsion and stretching increase along the Zn–O bond, as indicated by the increase in the angle between the two chelates from 81.14° to 137.00°. The increase in the Zn–O bond length from 1.927 to 2.180 Å indicates the beginning of the tautomeric transformation of the complex. As shown in Fig. 1d, the Zn–O bond reaches a maximum length of 2.976 Å as the H atom moves closer to the center of the complex. Figure 1e shows the final step in which the ligand substitution is completed when a 0.958-Å-long hydrogen bond formed with the O atom and the Zn2+ was successfully extracted from the complex.
Mechanism of the Dissociation Reaction
The relative energies for the transition states, intermediate, and products in the gas-phase reaction mechanism were calculated at the B3LYP/6-311++G** and MP2/6-311 + G(2df,2p) levels of theory. The calculated energy data are depicted in the reaction coordinate pathway in Fig. 2. The reaction starts when two H atoms approach the Zn(acac)2 complex. H atoms are then adsorbed, as shown by step (a) in the reaction pathway in Fig. 2. The chemical reactions involve several distinct steps including two transition states (steps (b) and (e)) and one intermediate step (step (d)). The first transition state (TS1) occurs when secondary bonds are constructed between the 2H atoms and the O atoms. The relative energy for TS1 was calculated to be 24.70 kcal/mol (Fig. 2). The initial transition reaction leads to twisted and stretched Zn–O bonds at a calculated energy of 19.66 kcal/mol (step (c)). This reaction cycle appears to be endothermic because the energy of the products is higher than the energy of the reactants. As the reaction proceeds, Zn2+ dissociates due to the breaking of Zn–O bonds; consequently, the O–H bonds become stronger, and TS2 is formed (step (d), Fig. 2). The calculated energy barrier for the dissociation of Zn2+ was found to be 61.78 kcal/mol. The reaction is terminated when the O–H bond is formed at a calculated energy of −95.18 kcal/mol (step (e)). The overall dissociation reaction can be then summarized as shown in Eq. (2).
The reaction coordinate diagram shows that the initial transition state was obtained at a lower energy barrier (24.70 kcal/mol) than the final transition state (61.78 kcal/mol). Thus, TS1 is considered to be the rate-limiting step on which the overall reaction kinetics depend. The reaction follows a typical interchange substitution mechanism profile as the secondary bonding with the square planar complex of Zn(acac)2 were detected at the reaction intermediates. Because the association of H atoms to the square planar complex is the longest step in the pathway, it can be considered to be the actual rate-determining step of the overall reaction. Hence, the reaction mechanism can be classified as an interchange substitution mechanism that is associatively activated.
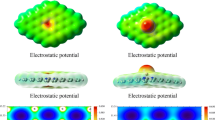
To validate Eq. (2), the byproduct of the dissociation reaction must be studied. In fact, the acetylacetonate anions might react with H atoms in various rapid reactions; however, the enol and keto tautomers of the acetylacetonate compound are mostly expected to occur in the gas phase. To predict the favored tautomer that is produced as a byproduct of the dissociation reaction, the spin density, electrostatic potential distribution, bond orders, and bond lengths were computed. Figure 3 shows the spin-density map (isosurfaces) merged with electrostatic potential topology (isocontours) for both tautomers of the acetylacetonate molecule. These maps were generated by plotting both properties over an electron density surface. The electrostatic potential map aims to indicate the distribution and concentration of the charges over the entire molecule. Thus, the blue isosurfaces at the added H atom of the acac enol indicate a high concentration of negative (or less positive) charges in this area, with a maximum electrostatic potential of 634 kJ. On the other hand, the acac keto exhibited weaker electrostatic attractions. Spin-density maps were used to show the distribution of spins (angular momentum of unpaired electrons) all over the molecules. In Fig. 3a, the red isocontours at the added H of the enol indicate high spins attributed to the lone pairs of the oxygen atoms. The difference between the number of unpaired electrons and the total spin density at the H atoms is a measure of the degree of covalent character of the hydrogen–ligand bonds. In contrast, for the keto tautomer, almost no spin is observed around the added H atom, indicating the lack of lone pairs. These observations suggest that the enol tautomer to be more stable than the keto tautomer in the gas phase.
To provide a more quantitative analysis of the stability of the resulting acac compound, the atomic charges are calculated (Table 1). Two approaches (electrostatic and Mulliken) were used to calculate the atomic charges to overcome the sensitivity of the calculations to basis set. The relatively large negative charge on the central atoms (C2) of both the enol and keto tautomers is attributed to the back-donation of O atoms. The charge at the keto C2 is higher than that at the enol C2, indicating that more charge alternation occurs in the enol tautomer, inducing higher aromaticity in the enol molecule. This is emphasized by the bond orders presented in Table 2; the C1–O1 and C3–O2 bond orders are greater for the keto form than for the enol form. Furthermore, the C1–C2 and C2–C3 bonds of the enol tautomer are stronger than those of the keto tautomer, as indicated by the increased bond orders and decreased bond lengths. This bond strengthening may also stabilize the three centers of the π bonds of the enol ring, enhancing the aromaticity of the ring. The strengths of the O1–H1, O2–H1, and C2–H1 bonds provide a final measure of the stabilities of both tautomers. The large charge separation between the O1 and H1 (Table 1) indicates a highly polarized O1–H1 secondary; the same case is observed for the O2–H1 bond. Therefore, the electron pair may shift from H towards the O of the C=O bond, inducing a dipole moment that is positive at the H side and negative at the O side. The dipole moment was calculated to be 4.8 Debye and is oriented at 38.9° from the C–O axis. This strong dipole moment results in the partial shifting of the electron charge from hydrogen to oxygen. Thus, the positive–negative attraction between the charges generated by this shift strengthens the hydrogen bonds, preventing the further dissociation of the O–H portion of one acetylacetonate group. However, the charge separation between H1 and C2 is much smaller than between the enol O–H bonds and is therefore less polarized. These facts, along with the bond orders and lengths listed in Table 2, indicate that the O–H bond of the enol tautomer is stronger than the C2–H1 bond of the keto tautomer. In fact, the data shown in Tables 1 and 2 emphasize that the O–H bond in the enol tautomer is much stronger than the intermolecular hydrogen bonds. Hence, it is clear that the acac enol is the favored byproduct of the Zn2+ dissociation reaction.
Simulation of IR Spectroscopy
The infrared (IR) spectrum corresponding to the growth of ZnO nanostructures onto a layer of graphene was simulated using the DFT approach. The computational details were described earlier in this article. Because there is a hydrogen stream inside the reactor that is used to decompose Zn2+ from its complex, it is appropriate to assume that the released Zn2+ ion will be transported to the graphene oxide surface by hopping among the free H atoms. Thus, for the IR simulation, the Zn2+ is replaced with the Zn–H group. The simulation depicts the changes that happen during bonding between atoms after Zn–H was adsorbed at the oxygen sites on the surface of the graphene layer. For each reaction step, the IR peaks corresponding to every bond stretching, breaking, and forming were captured and plotted in Fig. 4 against the optimized geometry of the structure. Figure 4(a) shows that during the first step of the reaction, in which Zn–H was adsorbed, a C=C peak corresponding to vibration out of bending was observed in the range of 700–900 cm−1; this can be observed clearly in the corresponding structure geometry. This peak is attributed to the restricted rearrangement of C atoms in the graphene network to accommodate the approaching Zn–H. Accordingly, peaks corresponding to C–C stretching were also observed in the range of 900–1100 cm−1.
Figure 4(b) shows peaks at 1448–1560 cm−1, which are attributed to the conversion of the carbonyl group from C=C–C=O into the transient structure C+–C=C–O+. During this conversion, the symmetry about the carboxylic group increased, and the two peaks corresponding to the symmetric O–C–O bond of the anionic carboxylate group (at 1448 cm−1) and the asymmetric O–C–O bond (at 1560 cm−1) agreed with the reported spectra of carboxylate complexes (Table 3) [34, 35]. The spectral peak is still premature (low intensity), which indicates that the conversion process is starting, with the double bonds beginning to break into single bonds with secondary bonds. Furthermore, an interesting peak was observed at 1220–1400 cm−1 (Fig. 4(c)). This peak is attributed to the C=C stretching among the graphene C network, which is also observed in the corresponding optimized structure. Such stretching could take place to overcome the lattice mismatch between graphene and the ZnO crystal.
As long as the reaction proceeds, the intensity of the previously stated peaks continues to change according to the continuous movement of the graphene oxide layer to accept the Zn–H group. The permanent bonds are constructed via the strong attachment of the Zn–H group to the oxygen sites. A remarkable peak was observed at 1730 cm−1 (Fig. 4(d)), indicating the complete transformation of the carbonyl group into C+–C=C–O+. In the next step of the simulation, a peak corresponding to Zn–O bond formation was detected (Fig. 4(e)) at 550 cm−1. In the corresponding geometry for the same simulation step, the Zn–H bonds have been constructed between the three surrounding O atoms. In fact, the Zn–O peak was observed in the early stages of the simulation with low transmittance intensity. These peaks could be captured as a result of the tendency of Zn2+ (as a Lewis acid) to form complexes dominated by highly directional covalent interactions with the oxygen networks before the Zn–O covalent bonds are finally formed.
Conclusions
In this study, we have investigated the gas-phase reactions involved in the deposition of zinc and the adsorption of Zn2+ to the oxygen network to produce ZnO/graphene composites. The energies of reactants, transition states, and products were calculated, and a reaction mechanism for the dissociation of Zn2+ from its complex was proposed. The energy barrier for the dissociation of Zn2+ from the acetylacetonate complex was found to be 61.78 kcal/mol. Furthermore, the results of a molecular orbital study indicated the complete abstraction of Zn2+ from the acetylacetonate complex. The calculated IR results were in good agreement with experimental IR results reported in literature, validating the findings of the current study. The proposed route of growth involves a self-terminating reaction due to H capping at the end of the H–Zn–3O group. This supports the possibility of achieving atomic layer deposition (ALD) rather than chemical vapor deposition (CVD) while deposition occurs from the gas phase.
References
Muszynski R, Seger B, Kamat PV. Decorating graphene sheets with gold nanoparticles. J Phys Chem C. 2008;112:5263–6.
Kim YJ, Hadiyawarman, Yoon A, Kim M. Hydrothermally grown ZnO nanostructures on few-layer graphene sheets. Nanotechnology. 2011;22:245603–11.
Kim YJ, Yoo H, Lee CH, Park JB, Baek H, Kim M, et al. Position- and morphology-controlled ZnO nanostructures grown on graphene layers. Adv Mater. 2012;24:5565–70.
Yan L, Zheng YB, Zhao F, Li S, Gao X, Xu B, et al. Chemistry and physics of a single atomic layer: strategies and challenges for functionalization of graphene and graphene-based materials. Chem Soc Rev. 2012;41:97–114.
Xiang Q, Yu J, Jaroniec M. Graphene-based semiconductor photocatalysts. Chem Soc Rev. 2012;41:782–96.
Aziz NSA, Nishiyama T, Rusli NI, Mahmood MR, Yasui K, Hashim AM. Seedless growth of zinc oxide flower-shaped structures on multilayer graphene by electrochemical deposition. Nanoscale Res Lett. 2014;9:337–46.
Aziz NSA, Mahmood MR, Yasui K, Hashim AM. Seed/catalyst-free vertical growth of high-density electrodeposited zinc oxide nanostructures on a single layer graphene. Nanoscale Res Lett. 2014;9:95–102.
Ahmad NF, Rusli NI, Mahmood MR, Yasui K, Hashim AM. Seed/catalyst-free growth of zinc oxide nanostructures on multilayer graphene by thermal evaporation. Nanoscale Res Lett. 2014;9:83–70.
Hilder M, Winther-Jensen O, Winther-Jensen B, MacFarlane DR. Graphene/zinc nano-composites by electrochemical co-deposition. Phys Chem Chem Phys. 2012;14:14034–40.
Lee JM, Pyun YB, Yi J, Choung JW, Park WI. ZnO nanorod − graphene hybrid architectures for multifunctional conductors. J Phys Chem C Nanomater Interfaces. 2009;113:19134–8.
Song WT, Xie J, Liu SY, Zheng YX, Cao GS, Zhu TJ, et al. Graphene decorated with ZnO nanocrystals with improved electrochemical properties prepared by a facile in situ hydrothermal route. Int J Electrochem Sci. 2012;7:2164–74.
Ambrozic G, Škapin SD, Zigon M, Orel ZC. The synthesis of zinc oxide nanoparticles from zinc acetylacetonate hydrate and 1-butanol or isobutanol. J Colloid Interface Sci. 2010;346:317–23.
Fan D, Zhang R, Wang X, Huang S, Peng H. Influence of silver dopant on the morphology and ultraviolet emission in aligned ZnO nanostructures. Phys Status Solidi A. 2012;209:335–9.
Musić S, Šarić A, Popović S. Formation of nanosize ZnO particles by thermal decomposition of zinc acetylacetonate monohydrate. Ceram Int. 2010;36:1117–23.
Singh T, Pandya DK, Singh R. Surface plasmon enhanced bandgap emission of electrochemically grown ZnO nanorods using Au nanoparticles. Thin Solid Films. 2012;520:4646–9.
Pengtao X, Qing T, Zhen Z. Structural and electronic properties of graphene–ZnO interfaces: dispersion-corrected density functional theory investigations. Nanotechnology. 2013;24:1–7.
Nasrin F, Serge A, Paul AC. Fe doped TiO 2 –graphene nanostructures: synthesis, DFT modeling and photocatalysis. Nanotechnology. 2014;25:305601–12.
Sousa SF, Carvalho ES, Ferreira DM, Tavares IS, Fernandes PA, Ramos MJ, et al. Comparative analysis of the performance of commonly available density functionals in the determination of geometrical parameters for zinc complexes. J Comput Chem. 2009;30:2752–63.
Raghavachari K. Perspective on “Density functional thermochemistry. III. The role of exact exchange”. Theor Chem Acc. 2000;103:361–3.
Becke AD. Perspective: fifty years of density-functional theory in chemical physics. J Chem Phys. 2014;140:301–19.
Perdew JP, Ruzsinszky A, Constantin LA, Sun J, Csonka GBI. Some fundamental issues in ground-state density functional theory: a guide for the perplexed. J Chem Theory Comput. 2009;5:902–8.
Bader RFW. The density in density functional theory. Theochem. 2010;943:2–18.
Becke AD. A density-functional approximation for relativistic kinetic energy. J Chem Phys. 2009;131:244118–23.
Becke AD. A new mixing of Hartree-Fock and local density-functional theories. J Chem Phys. 1993;98:1372–7.
Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–52.
Becke AD. Density-functional thermochemistry. II. The effect of the Perdew-Wang generalized-gradient correlation correction. J Chem Phys. 1992;97:9173–7.
Schmider HL, Becke AD. Density functionals from the extended G2 test set: Second-order gradient corrections. J Chem Phys. 1998;109:8188–99.
Schmider HL, Becke AD. Optimized density functionals from the extended G2 test set. J Chem Phys. 1998;108:9624–31.
Hertwig RH, Koch W. On the parameterization of the local correlation functional. What is Becke-3-LYP? Chem Phys Lett. 1997;268:345–51.
Adejoro I, Oyeneyin O, Obaleye JA. Characterization of a novel polymeric Zinc (II) complex containing the anti-malarial Quinine as ligand: A Theoretical Approach (Semi-empirical and DFT methods). Am J Sci Ind Res. 2013;4:111–22.
Hehre WJ. Theoretical models. In: Pople JA, editor. A Guide to Molecular Mechanics and Quantum Chemical Calculations. USA: Wavefunction. Inc.; 2003. p. 385–445.
Dixon DA, Dunning TH, Eades RA, Gassman PG. Generalized valence bond description of simple ylides. J Am Chem Soc. 1983;105:7011–7.
Hehre WJ, Radom L, Schleyer PVR, Pople JA. Ab initio molecular orbital theory. In: Leach AR, editor. Molecular Modeling. New Jersey: Prentice Hall; 2001. p. 1–793.
Goncalves G, Marques PAAP, Granadeiro CM, Nogueira HIS, Singh MK, Grácio J. Surface modification of graphene nanosheets with gold nanoparticles: the role of oxygen moieties at graphene surface on gold nucleation and growth. Chem Mater. 2009;21:4796–802.
Rani JR, Lim J, Oh J, Kim JW, Shin HS, Kim JH, et al. Epoxy to carbonyl group conversion in graphene oxide thin films: Effect on structural and luminescent characteristics. J Phys Chem C. 2012;116:19010–7.
Acknowledgements
AAA thanks Malaysia-Japan International Institute of Technology (MJIIT) for the scholarship. This work was supported by Nippon Sheet Glass Corp, Hitachi Foundation, MJIIT, Universiti Teknologi Malaysia, Malaysia Ministry of Education and Malaysia Ministry of Science, Technology and Innovation through various research grants.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing Interests
The authors declare that they have no competing interests.
Authors’ Contributions
AAA designed and performed the simulations, participated in the data analysis, and prepared the manuscript. AMH monitored the simulation work, data analysis, discussion, and revision of the manuscript. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ali, A.A., Hashim, A.M. Density Functional Theory Study of Atomic Layer Deposition of Zinc Oxide on Graphene. Nanoscale Res Lett 10, 299 (2015). https://doi.org/10.1186/s11671-015-1008-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s11671-015-1008-y