Abstract
Evaluations of the lateral properties of timber joints are necessary to ensure the safety of timber buildings. The yield load is an important property that is usually obtained using authorized engineering techniques. Although yield loads have been easily obtained using authorized techniques, events that have occurred in the joint during yielding have not been clarified. This study experimentally obtains elastic limit data using nailed joints. Mechanical tests measuring the residual displacement after various lateral loads with six-joint specimen specifications were conducted. In this study, the load at which the residual displacement reached 5% of the nail diameter was defined as the elastic limit. The experimentally obtained elastic limits were compared with the yield loads obtained using authorized engineering techniques. The ratios of elastic limits to the yield loads obtained using the perfect elasto-plastic model, method described in EN, and 5% offset method were 0.554–0.743, 0.557–0.834, and 0.648–0.801, respectively. The results numerically revealed that residual displacements occurred at a much lower load than the yield loads.
Similar content being viewed by others
Introduction
Nailed joints connecting solid wood and board materials are commonly used in timber structures. A widely known example is the panel-sheathed shear wall, which connects a wooden frame and board materials with nails. Several researchers have revealed that the in-plane shear performance of a shear wall is dominated by the lateral resistance of nailed joints. Tuomi and McCutcheon blazed the trail of mechanical analyses estimating the shear strength of shear walls using the lateral loading test results of nailed joints [1]. Several researchers have attempted to develop a mechanical model for estimating the elasto-plastic behavior of walls using the test results of nailed joints [2,3,4,5,6]. In the mechanical models constructed in these studies, the wooden frame and board material were regarded as rigid bodies; their results revealed that the shear deformation of the wall can be expressed by the slip deformation of the nailed joints. Some studies have included other factors (e.g., the shear buckling of board materials [7, 8], the bending of a wooden frame [9, 10], and a pull-out of a column form beam [11]) in their mechanical models; however, the consensus is that the slip of nailed joints is a main factor in the deformed wall. Recently, the structural design method, which enables the calculation of the shear properties of walls using the lateral properties of nailed joints, has been proposed and has become widely used [12, 13].
Evaluating the lateral resistance of nailed joints has been an important issue in the academic and practical areas of timber structures for several years. Many tests have been conducted, and a large quantity of characteristic data has been collected [14]. The yield load is one of the most important characteristics for designing structural timber elements. The yield load is known as the load value, and is located just over the elastic limit of the load–deformation relationship; moreover, it represents the starting point of plastic deformation. However, for timber joints, the yield point is difficult to decipher visually from the load–deformation relationship because the relationship shows a gradual shift from elastic to plastic behavior. Therefore, engineering techniques for determining the yield load from the relationship (their details are described later) have been proposed worldwide. These techniques enable the objective evaluation of joint properties.
Although engineering techniques have contributed to the development of academic knowledge and practical timber structures, problems remain. Researchers and engineers who use these techniques can obtain the yield load; however, the true mechanical situation of the joint at the obtained load is unclear. The authors emphasize the importance of clarifying what occurs in the joint at the obtained yield load. Accordingly, the authors have attempted to collect various experimental data to clarify what occurs at the load regarded as the yielding point. This study focuses on the residual displacement and compares the starting point of residual displacement (the so-called elastic limit [15]) with the yield load as determined by engineering techniques.
Materials and methods
Nailed joint specimen
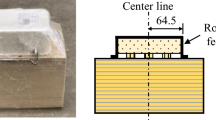
A nailed joint specimen [16] for the lateral load was prepared, as shown in Fig. 1. Two side panels were mounted on the main member with four nails. Three wood species with different densities were chosen as the main members: Japanese cedar (Cryptomeria japonica), spruce, and Japanese larch (Larix kaempferi). For preparing the spruce specimen, the authors bought several lots of SPF dimension lumber, and picked out spruce from them. The authors confirmed that Engelmann spruce (Picea engelmannii) was included, but other types of spruce might be included in the lots. The densities are listed in Table 1. The size of the main member was 38 × 89 mm by cross section and 300 mm in length. Structural plywood with a 5-ply and a 12 mm thickness made of Japanese cedar, representing class 2 structural plywood according to JAS [17], and structural medium density fiberboard (MDF) of a 9-mm thickness, classified as type M-30 according to JIS [18], were used as side panels. The size of the side panels was 100 × 300 mm. CN50 nails [19], with a trunk diameter of 2.87 mm and a length of 50.8 mm, were used to connect the main member and side panels. Therefore, using three species of main members and two types of side panels, this study conducted tests with six specifications of the nailed specimen. For specimens using plywood, the plywood was set so that the fiber direction of the outer veneer was parallel to the loading direction. A Teflon sheet and grease were inserted to remove the friction between the main member and side panel, as shown in Fig. 1. According to our previous study, the coefficient of friction becomes 0.1 or lower with the method [20]. Therefore, the effect of friction was ignored in our upcoming discussion of the test results.
Loading methods
A lateral loading test was conducted using a universal testing machine (Shimadzu Co. Ltd., AG-1 250 kN). A downward load is applied to the top face of the main member, as shown in Fig. 1. Thus, a slip between the main member and side member occurred. In this study, two loading methods were applied. The first was to evaluate the yield load of the joints using authorized engineering techniques, and the second was to measure the residual displacement.
The first loading method used was monotonic loading, which is commonly utilized to evaluate the lateral resistance of timber joints. A downward load with a continuous loading speed was applied from the start to the end of testing, and the expected load–displacement relationship is shown as a black line in Fig. 2. The load was applied at a speed of 2.0 mm/min. After reaching its maximum, the load was applied until it reached 80% of the maximum or the displacement reached 30 mm. The load applied to the specimen and the relative displacement between the main member and the side panels were recorded during the test. A load cell (Tokyo Measuring Instruments Laboratory Co. Ltd., SFL-50kNNAG; capacity: 50 kN) was used to measure the load. Two displacement transducers (SDP-100C, capacity: 100 mm, Tokyo Measuring Instruments Laboratory Co. Ltd.) were attached to the opposite sides of the main member, and the targets were attached to the side panels. The average of the values obtained from the two transducers was used as the displacement. Ten replicates were assigned to each specification, and 60 specimens were tested. In larch–MDF, the data of two specimens were removed due to an accident occurred during testing.
The second loading method utilized was reversed loading. When the load was reached at our preset target load Pt, unloading started until the load became zero. The expected load–deformation relationship is shown as a red line in Fig. 2. The displacement at the end of the unloading was adopted as the residual displacement. In this study, the displacement transducers were changed to an instrument that could precisely record the displacement (Tokyo Measuring Instruments Laboratory Co. Ltd., CDP-25; capacity: 25 mm). The target load, Pt, was set at various values, as listed in Table 2. The lowest was 0.1 kN per nail. The highest target load at each specification was sufficiently greater than the yield loads obtained by the monotonic loading tests. The replicates were determined while accumulating the experimental data until a reliable discussion could be formulated. The replicates of the reversed loading tests are listed in Table 2, and a total of 385 specimens were tested. The difference in density between the groups was minimized when the specimens were divided into target load groups.
Yield load
There are many methods for determining yield load, and obtained values are slightly different among them. For comparing the elastic limit and yield load, discussion with only one method seems not to be appropriate. In this study, four popular methods were applied for obtaining the yield load.
Three authorized engineering techniques were applied to obtain the yield load using the load–displacement relationship. The first was a perfect elasto-plastic model (EPM) [13, 21]. Although this method was originally proposed for analyzing wood-frame structures, there are many examples of researchers applying it to joint analyses [22,23,24,25]. The method for determining the yield load is illustrated in Fig. 3a. The black line indicates the load–displacement relationship obtained from the test. First, direct lines I and II were drawn between 0.1 Pmax and 0.4 Pmax as well as 0.4 Pmax and 0.9 Pmax, respectively, based on the relationship (where Pmax is the maximum load). Line II shifts until it meets the load–displacement relationship, and the shifted line is named Line III. The load value at the intersection of Lines I and III represents the yield load.
The second method is described in EN 12512 [26] (referred to as EN). As shown in Fig. 3b, the direct Line I was drawn between 0.1 Pmax and 0.4 Pmax. Next, the second Line II was drawn so that its incline became 1/6 of the incline of Line I and it meets the load–displacement relationship. The load value at the intersection of Lines I and II represents the yield load.
The third method is described in ASTM D5652-21 [27] (referred to as OSM). Although the method is for bolted joints, it was also applied to nailed joints [28]. To determine the yield load, a straight line was fitted to the initial linear portion of the load–displacement curve. In the ASTM standard, there are no precise descriptions of the method for drawing a straight line. In this study, the authors drew the line using the least squares method for the data plots between 0.1 Pmax to 0.4 Pmax. The line was offset by a displacement of 5% of the nail diameter. The yield load represents the load at which the offset line intersects the load–displacement relationship, as shown in Fig. 3b.
Johansen theory [29], which is well known as European yield theory (EYT) in Japan, is the most popular method to obtain the yield load using material characteristic values. The Architectural Institute of Japan [30] following Johansen theory, and yield load Py was calculated using the following equation:
where Fe and Feʹ indicate the embedment strengths of the main member and board material, respectively. F indicates the nail strength. d indicates the nail diameter. l and lʹ indicate the inserted length of the nail in the main member and thickness of the board material, respectively. The authors additionally conducted embedment tests and bending test [31] for calculating the yield load with the equation. Figure 4a shows the experimental setup of embedment test for solid wood. Clear wood specimens were cut from the joint specimens, and the embedment load parallel to the grain was applied with a nail to the top surface of the specimen. Ten replicates were assigned to each wood species. Figure 4b shows the experimental setup of embedment test for board material. Small board material specimens were obtained from the joint specimens. With fixing the lower part with a bolt, a nail inserted to the upper part was loaded upward. During the embedment tests, load and displacement were recoded. Ten replicates were assigned to each board type. Figure 4c shows the bending test for nail. Three-point bending test with the span of 32 mm was conducted. After conducting these tests, strength was obtained from load–deformation relationship. As the same with OSM, the straight line for initial stiffness was offset by a displacement of 5% of the nail diameter. The load at which the offset line intersects the load–displacement relationship was used for obtaining the strength [31]. For obtaining the embedment strengths, stress was calculated by dividing the load by loading area. For obtaining the nail strength, the bending stress was calculated with the load. In this study, the calculated yield load is denoted as EYT.
Results and discussion
Yield load obtained via the monotonic loading test
The load–displacement relationships are shown in Fig. 5. In all specifications, a straight linear behavior was observed at the beginning of loading. The slope of the relationship gradually decreased with an increase in displacement. After reaching the maximum load, the load gradually decreased, and no brittle failures occurred in any of the specimens. Regarding the differences in materials, the specifications using the main member with the highest density showed the highest resistance. The specifications using MDF showed a higher resistance than that of the plywood. For MDF, the displacement at the maximum load appeared to be smaller than that of the plywood. Although the specimens using plywood reached their maximum load at approximately 15–20 mm in displacement, many specimens using MDF reached a maximum load less than 10 mm in displacement, especially for cedar–MDF and spruce–MDF.
The averages and standard deviations of the yield loads obtained using the three techniques are listed in Table 3. In comparing the differences between the techniques, the EPM shows the highest value and OSM shows the lowest value in most of specifications. A multiple comparison test (Bonferroni method) was conducted to verify the difference due to the techniques. The significant differences between EPM and OSM were recognized in all of specifications, a significant difference between EPM and EN were recognized in the specification of cedar–MDF, and a significant difference between EN and OSM were recognized in the specification of larch–plywood at a significant level 0.05. The results indicate that the yield load may differ depending on what was chosen by the users. On the load–displacement relationships in Fig. 5, the yield loads obtained using EPM, EN and OSM are plotted with yellow round, red rhombus, and blue squares, respectively. The yield load from EPM was plotted where the load–displacement relationships started to decrease in slope. This result was also observed in previous study by one of the authors [32].
The values used to calculate EYT are listed in Table 4, which are average values obtained from the embedment tests and bending test. The calculated results are listed in Table 3. Although the following is not the direct purpose of this study, the authors touch about the comparisons between EYT and the other yield loads. The EYT is higher than the OSM in all the specifications. In the specifications using plywood, EYT is higher than EPM, whereas similar or lower yield loads can be observed in the cases using MDF. The reason for the difference between the EYT and experimentally obtained values has not been clarified in this study, but one possible reason is that the values of EYT were obtained with the assumption that the materials behave as rigid-plastic, which may different from actual behavior especially in the cases using low-embedment strength materials.
Load–deformation relationship and residual displacements obtained by the reversed loading test
Examples of load–deformation relationships are shown in Fig. 6. For a small target load, the relationship during loading shows linear behavior, and relatively minimal residual displacement is observed after unloading. The gradual decrement of the slope in the linear relationship and large residual displacement were observed using the increment of the target load (e.g., Pt = 0.25 kN or more in Fig. 6a, Pt = 0.60 kN or more in Fig. 6b).
The residual displacements obtained from the load–displacement relationships are shown in Fig. 7. The round plots indicate the mean value at each target load and the error bars indicate the standard deviation. For example, in the cedar–plywood (Fig. 7a), when the target load was lower than 0.30 kN, the residual displacements appeared to be small and could be regarded as almost zero. However, when a target load of over 0.30 kN occurred, the plots were separated from the horizontal axis. With an increase in the target load, the residual displacement exponentially increased. From the results, the elastic limit [15] seems to be approximately 0.30 kN. The specifications with the highest yield loads exhibited the highest elastic limits. For example, the elastic limit for larch–MDF was approximately 0.50 kN in the target load.
Comparison of elastic limit and yield loads obtained using various methods
To compare the elastic limit and yield loads, it was necessary to obtain an accurate value of the elastic limit. According to Goodno and Gere [15], the elastic limit represents the load that will be reached wherein all the displacement is recovered during unloading. Based on the load–displacement relationship (Fig. 6), it is difficult to search for the target load in which the residual displacement is perfectly zero, because a small residual displacement will appear even for a small target load. There is no authorized method for defining the elastic limit; therefore, this study calculated the elastic limit as the load when the residual displacement became 5% of the nail diameter. The average values (plots in Fig. 7) were linearly interpolated to determine the load at which the residual displacement was 0.1435 mm.
The elastic limits are presented in Table 5. For the specification using plywood, the elastic limits were 0.282, 0.285, and 0.297 kN. When MDF was used, the elastic limits were 0.476, 0.420, and 0.512 kN, respectively. A possible reason for the difference in values is that plywood is a material that easily undergoes residual deformation, so the elastic limits of joints using plywood are dominated by the wood’s properties. Although spruce–MDF showed a higher yield load than cedar–MDF in the monotonic loading test, a lower elastic limit occurred. This suggests that the elastic limit is not directly related to the yield load. However, this research used only three species of main members, and additional tests with more species are required to ensure a reliable discussion.
Table 5 also lists the ratios of the elastic limit to the yield loads. In most specifications, the ratios were less than 1, which means that the elastic limit was sufficiently lower than the yield loads. For EPM, the ratios at specification using plywood were 0.554–0.606, thereby suggesting that residual displacement occurs in almost half of the EPM. The ratios of the specifications using MDF were 0.642–0.743, which were higher than that of plywood. Similar values were observed for the ratios of EN and EYT. Although the yield load of OSM was lower than those of EPM and EYT (Table 3), the elastic limits were lower than those of OSM, and the ratios were 0.628–0.801. These results reveal that the residual displacements of the nailed joints were much lower than those of the yield loads.
Finally, the residual displacements occurred at the yield loads were calculated. The results are listed in Table 6. The average values (plots in Fig. 7) were linearly interpolated to determine the residual displacement at yield load. From the table, it is revealed that non-negligible displacements are remained at the yield loads. In the joints using plywood, residual displacement became over 1 mm when the yield loads were determined with European yield theory. Although OSM was a lowest yield load, 0.284–0.687 mm remained at the load. Currently, it is difficult to judge clearly whether the residual displacement in Table 6 is a serious matter for the safety of timber structures or not. If it becomes a serious matter, the new evaluating technique of yield load which shows the lower yield load than presenting methods will be required.
Conclusion
The residual displacements of nailed joints under lateral loads were experimentally measured, and relevant elastic limits were obtained. These elastic limits were approximately 0.3 kN in the cases of joints using plywood as a side panel. For MDF, the elastic limits were 0.420–0.512 kN, which differed from the species used in the main member. In comparing the elastic limits with yield loads obtained with widely used techniques, the formers were much lower than the latter; the ratios of elastic limits to the yield load with the perfect elasto-plastic model, method described in EN, and 5% offset method were 0.554–0.743, 0.557–0.834, and 0.648–0.801, respectively. The results also showed that residual displacements occurred at much lower loads than the yield loads. It was also revealed that non-negligible displacements remained after yielding. Especially, the residual displacement become over 1 mm in the case of nailed joints using plywood when the yield load is determined with European yield theory.
Availability of data and materials
All data discussed during this study are included in this published article.
Abbreviations
- P t :
-
Target load
- P max :
-
Maximum load
- P y :
-
Yield load
- F e :
-
Embedment strengths of the main member
- F eʹ:
-
Embedment strengths of the board material
- F :
-
Nail strength
- d :
-
Nail diameter
- l :
-
Inserted length of the nail in the main member
- lʹ:
-
Thickness of the board material
References
Tuomi RL, McCutcheon WJ (1978) Racking strength of light-frame nailed walls. J Struct Div 104:1131–1140
Kamiya F (1981) Theoretical studies on racking stiffness and strength of wooden sheathed walls. Trans AIJ 56:86–94
Easley JT, Foomani M, Dodds RH (1982) Formulas for wood shear walls. J Struct Eng 108:2460–2478
McCutcheon WJ (1985) Racking deformations in wood shear walls. J Struct Eng 111:257–269
Schmidt RJ, Moody RC (1989) Modeling laterally loaded light-frame buildings. J Struct Eng 115:201–207
Ogawa K, Sasaki Y, Yamasaki M, Fukuta S (2015) Theoretical estimation of mechanical properties of plywood-sheathed shear wall with combined use of adhesive tape and wood dowels. Wood Fiber Sci 47:421–430
Murakami M, Azumi Y, Oshita Y (2015) Experimental study on relationship between shear buckling and shear failure of nailed sheathed shear walls. J Struct Constr Eng, AIJ 80(716):1569–1578
Murakami M, Azumi Y (2017) Study on structural calculation method of nailed sheathed shear walls under shear force considering shear buckling and shear failure of sheets. J Struct Constr Eng, AIJ 82(732):239–246
Gupta AK, Kuo GP (1985) Behavior of wood-framed shear wall. J Struct Eng 111:1722–1733
Murakami M, Azumi Y, Inayama M (2012) Formula to predict shear stiffness of sheathed wall considering flexural stiffness of vertical studs and its verification with numerical analyses. J Struct Constr Eng, AIJ 77(672):249–258
Sudo R, Kawahara H, Ochiai Y, Aoki K, Inayama M (2021) Detailed verification on the performance of nailed joints in the panel sheathed shear wall. J Struct Constr Eng, AIJ 86(784):945–956
Murakami M, Inayama M (1999) Formulae to predict the elastic and plastic behavior or sheathed walls with any nailing arrangement pattern. J Struct Constr Eng, AIJ 519:87–93
Working group for revising the manuscript of the allowable stress design for wooden framework method (2017) In: Committee for revising the allowable stress design for wooden framework method (ed) Allowable stress design for wooden framework method. Japan Housing and Wood Technology Center, Tokyo
Ogawa K (2018) Domestic studies on shear resistance of nailed timber joint. Mokuzai Kogyo 73(1):2–7
Goodno BJ, Gere JM (2017) Elasticity, plasticity, and creep. In: Mechanics of materials, 9th ed SI. Cengage learning, Connecticut, pp 38–44
JAS 0360 (2019) Structural panel. Japan Agricultural Standard. https://www.maff.go.jp/j/jas/jas_kikaku/attach/pdf/kikaku_itiran2-334.pdf. Accessed 10 May 2022
JAS (2019) Plywood. Japan Agricultural Standard. https://www.maff.go.jp/j/jas/jas_kikaku/attach/pdf/kikaku_itiran2-235.pdf. Accessed 10 May 2022
Japanese standards association (2014) Fiberboard JIS A 5905, Tokyo
Japanese standards association (2009) Nails JIS A 5508, Tokyo
Ogawa K, Mori R, Kobayashi K (2021) Verification of general methods for inhibiting friction used in mechanical tests of timber joints. Mokuzai Kogyo 76(10):376–381
Yasumura M, Kawai N (1998) Estimating seismic performance of wood-frame structures. In: Proceedings of the 5th world conference on timber engineering (WCTE). Montreal, Switzerland, 1998, 564–571
Wanyama OG, Sawata K, Hirai T, Koizumi A, Sasaki Y (2012) Effective lateral resistance of timber–plywood–timber joints connected with nails. J Wood Sci 58:315–321
Ueda R, Sawata K, Takanashi R, Sasaki Y, Sasaki T (2020) Degradation of shear performance of screwed joints caused by wood decay. J Wood Sci 66:42
Ogawa K, Fukuta S, Kobayashi K (2020) Experimental study of lateral resistance of bolted joints using Japanese cedar (Cryptomeria japonica) treated with resin impregnation. J Wood Sci 60:71
Kržan M, Azinović B (2021) Cyclic response of insulated steel angle brackets used for cross-laminated timber connections. Eur J Wood Prod 79:691–705
EN 12512 (2002) Timber structures—test methods—cyclic testing of joints made with mechanical fasteners. European Committee for Standardization (CEN), Brussels
ASTM D5652-21 (2021) Standard test method for single-bolt connections in wood and wood-based products. ASTM International, West Conshohocken.
Sawata K, Sasaki Y (2018) Lateral strength of nailed timber connection with decay. J Wood Sci 64:1734
Johansen KW (1948) Theory for timber connection. Int Assoc Bride Struct Eng 9:249–262
Yasumura M (2011) Timber joints using dowel type connections. In: Architectural Institute of Japan (ed) Standard for structural design of timber structures. Maruzen publishing, Tokyo, pp 222–238
Kawai N (2011) General test method for joints. In: Architectural Institute of Japan (ed) Standard for structural design of timber structures. Maruzen publishing, Tokyo, pp 369–376
Ogawa K, Harada M, Shibusawa T, Miyamoto K (2018) Single shear properties and deformation behavior of nailed joints using various structural panel materials. Mokuzai Gakkaishi 64(4):139–148
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
NW and KO designed and performed the experiments and analyzed the data. KK participated in the discussions on data interpretations. NW and KO wrote the manuscript in consultation with KK. All authors read and approve the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Watanabe, N., Ogawa, K. & Kobayashi, K. Comparison of the elastic limit and yield load of nailed joints connecting solid wood and wood-based board material. J Wood Sci 68, 42 (2022). https://doi.org/10.1186/s10086-022-02050-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s10086-022-02050-5