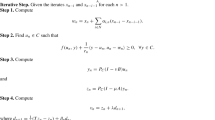Implicit iteration scheme for phi-hemicontractive operators in arbitrary Banach spaces

Abstract

The purpose of this paper is to characterize the conditions for the convergence of the implicit Mann iterative scheme with error term to the unique fixed point of ϕ-hemicontractive mappings in a nonempty convex subset of an arbitrary Banach space.

MSC (2000)

primary: 47H10, 47H17; secondary: 54H25

Introduction

Let K be a nonempty subset of an arbitrary Banach space X and X^∗ be its dual space. Let T:D(T) ⊆X→X be a mapping. The symbols D(T), R(T), and F(T) stand for the domain, the range, and the set of fixed points of T, respectively (for a single-valued map T:X→X, x∈X is called a fixed point of T if T(x)=x). We denote by J the normalized duality mapping from X to $2^{X^{\ast }}$ defined by

$$J\left(x\right)=\left\{f^{\ast }\in X^{\ast }:〈x,f^{\ast }〉={∥x∥}^2={∥f^{\ast }∥}^2\right\}.$$

Definition 1

The mapping T is called Lipshitzian if there exists L>0 such that

$$∥\mathit{\text{Tx}}-\mathit{\text{Ty}}∥⩽L∥x-y∥,$$

for all x,y∈K. If L=1, then T is called nonexpansive, and if 0⩽L<1,T is called contraction.

Definition 2

[1–4]

(i) T is said to be strongly pseudocontractive if there exists t>1 such that for each x, y∈D(T), there exists j(x−y)∈J(x−y) satisfying

$$\text{Re}〈\mathit{\text{Tx}}-\mathit{\text{Ty}},j(x-y)〉\le \frac{1}{t}\parallel x-y{\parallel }^2.$$

(ii) T is said to be strictly hemicontractive if F(T)≠∅ and there exists a t>1 such that for each x∈D(T) and q∈F(T), there exists j(x−y)∈J(x−y) satisfying

$$\text{Re}〈\mathit{\text{Tx}}-q,j(x-q)〉\le \frac{1}{t}\parallel x-q{\parallel }^2.$$

(iii) T is said to be ϕ-strongly pseudocontractive if there exists a strictly increasing function ϕ:[0,∞)→[0,∞) with ϕ(0)=0 such that for each x, y∈D(T), there exists j(x−y)∈J(x−y) satisfying

$$\text{Re}〈\mathit{\text{Tx}}-\mathit{\text{Ty}},j(x-y)〉\le \parallel x-y{\parallel }^2-\varphi (\parallel x-y\parallel )\parallel x-y\parallel .$$

(iv) T is said to be ϕ-hemicontractive if F(T)≠∅ and there exists a strictly increasing function ϕ:[0,∞)→[0,∞) with ϕ(0)=0 such that for each x∈D(T) and q∈F(T), there exists j(x−y)∈J(x−y) satisfying

$$\text{Re}〈\mathit{\text{Tx}}-q,j(x-q)〉\le \parallel x-q{\parallel }^2-\varphi (\parallel x-q\parallel )\parallel x-q\parallel .$$

Clearly, each strictly hemicontractive operator is ϕ-hemicontractive.

Chidume [1] established that the Mann iteration sequence converges strongly to the unique fixed point of T in case T is a Lipschitz strongly pseudocontractive mapping from a bounded closed convex subset of L _p (o r l _p ) into itself. Afterwards, several authors generalized this result of Chidume in various directions [2, 4–11].

In 2001, Xu and Ori [12] introduced the following implicit iteration process for a finite family of nonexpansive mappings {T _i :i∈I} (here, $I=\{1,2,\dots ,N\}$), with {α _n } a real sequence in (0,1), and an initial point x₀∈K:

$$\begin{array}{rl}{x}_1& =(1-{\alpha }_1)x_0+{\alpha }_1{T}_1{x}_1,\\ x_2& =(1-{\alpha }_2)x_1+{\alpha }_2{T}_2{x}_2,\\ ⋮\\ x_N& =(1-{\alpha }_N)x_{N-1}+{\alpha }_N{T}_N{x}_N,\\ x_{N+1}& =(1-{\alpha }_{N+1})x_N+{\alpha }_{N+1}{T}_{N+1}{x}_{N+1},\\ ⋮\end{array}$$

which can be written in the following compact form:

$$x_n=(1-{\alpha }_n)x_{n-1}+{\alpha }_n{T}_n{x}_n,\text{for all}n\ge 1,$$

(XO)

where T _n =T_{n (mod N)} (here, the mod N function takes the values in I). Xu and Ori [12] proved the weak convergence of this process to a common fixed point of the finite family of nonexpansive mappings defined in a Hilbert space. They further remarked that it is yet unclear what assumptions on the mappings and/or the parameters {α _n } are sufficient to guarantee the strong convergence of the sequence {x _n }.

In [13], Chidume et al. proved the following results:

Lemma 3

[13]Let E be a real Banach space. Let K be a nonempty closed and convex subset of E. Let T : K→K be a strictly pseudocontractive map in the sense of Browder and Petryshyn. Let x^∗∈F(T). For a fixed x₀∈K, define a sequence {x _n } by

$$x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n,$$

where {α _n } is a real sequence in [0,1] satisfying the following conditions: (i)$\sum _{n=1}^{\infty }{\alpha }_n=\infty$and (ii)$\sum _{n=1}^{\infty }{\alpha }_n^2<\infty$. Then, (a) lim infn→∞∥x _n −T x _n ∥=0, (b) {x _n } is bounded and limn→∞∥x _n −x^∗∥ exists.

Theorem 4

[13]Let E be a real Banach space. Let K be a nonempty closed and convex subset of E. Let T: K→K be a strictly pseudocontractive map in the sense of Browder and Petryshyn with F(T):={x∈K:T x=x}≠∅. For a fixed x₀∈K, define a sequence {x _n } by

$$x_{n+1}=(1-{\alpha }_n)x_n+{\alpha }_{n}T{x}_n,$$

where {α _n } is a real sequence satisfying the following conditions: (i)$\sum {\alpha }_n=\infty$and (ii)$\sum \underset{n}{\overset{2}{\alpha }}<\infty$. If T is demicompact, then {x _n } converges strongly to some fixed point of T in K.

In [14], Osilike proved the following results:

Theorem 5

Let E be a real Banach space and K be a nonempty closed convex subset of E. Let {T _i : i∈I} be N strictly pseudocontractive self-mappings of K with$F=\bigcap _{i=1}^{N}F\left(T_i\right)\ne \varnothing$. Let${\left\{{\alpha }_n\right\}}_{n=1}^{\infty }$be a real sequence satisfying the following conditions:

$$\begin{array}{l}\left(i\right)0<{\alpha }_n<1,\\ \left(\mathit{\text{ii}}\right)\sum _{n=1}^{\infty }(1-{\alpha }_n)=\infty ,\\ \left(\mathit{\text{iii}}\right)\sum _{n=1}^{\infty }{(1-{\alpha }_n)}^2<\mathrm{\infty .}\end{array}$$

From arbitrary x₀∈K, define the sequence {x _n } by the implicit iteration process (XO). Then, {x _n } converges strongly to a common fixed point of the mappings {T _i : i∈I} if and only if$\underset{n\to \infty }{lim}infd(x_n,F)=0$.

In [15], Su and Li proved the following results:

Theorem 6

[15]Let E be a real Banach space and K be a nonempty closed and convex subset of E. Let${\left\{T_i\right\}}_{i=1}^N$be N strictly pseudocontractive self-maps of K in the sense of Browder and Petryshyn such that$F=\bigcap _{i=1}^{N}F\left(T_i\right)\ne \varphi ,$where F(T _i )={x∈K:T _i x=x}. For a fixed x₀∈K, define a sequence${\left\{x_n\right\}}_{n=1}^{\infty }$by

$$\begin{array}{ll}{x}_n& ={\alpha }_n{x}_n+(1-{\alpha }_n)T{y}_n,\\ y_n& ={\beta }_n{x}_n+(1-{\beta }_n)T{y}_n,\end{array}$$

where T _n =T_{n modN}and${\left\{{\alpha }_n\right\}}_{n=1}^{\infty },{\left\{{\beta }_n\right\}}_{n=1}^{\infty }$be real sequen– ces in [0,1] satisfying the following conditions: (i)$\sum _{n=1}^{\infty }(1-{\alpha }_n)=\infty$, (ii)$\sum _{n=1}^{\infty }{(1-{\alpha }_n)}^2<\infty ,$(iii)$\sum _{n=1}^{\infty }(1-{\beta }_n)<\infty ,$and (iv) (1−α _n )(1−β _n )L²<1. Then, (a) lim infn→∞∥x _n −T _n x _n ∥=0 and (b) limn→∞∥x _n −x^∗∥ exist for all x^∗∈F.

Remark 7

(i) One can easily see that for${\alpha }_n=1-\frac{1}{n^{\frac{1}{2}}}$, $\sum {(1-{\alpha }_n)}^2=\infty$. Hence, the results of Osilike[14]and Su and Li[15]are to be improved.

(ii) Proofs of Chidume et al.[13]main results based on ϕ⁻¹: Let us define ϕ:[0,∞)→[0,∞) by$\varphi \left(\alpha \right)=\frac{3^{\alpha }-1}{3^{\alpha }+1}$, then it can be easily seen that (i) ϕ is increasing and (ii) ϕ(0)=0, but$\underset{\alpha \to \infty }{lim}\varphi \left(\alpha \right)=1$and ϕ⁻¹(2) make no sense.

The purpose of this paper is to characterize the conditions for the convergence of the implicit iterative scheme with error term in the sense of [16–18] to the unique fixed point of ϕ-hemicontractive mappings in a nonempty convex subset of an arbitrary Banach space. Our results extend and improve most of the results in recent literature [7, 12–14, 19–22].

Preliminaries

The following results are now well known:

Lemma 8

[23]For all x, y∈X and j(x+y)∈J(x+y),

$$\parallel x+y{\parallel }^2\le \parallel x{\parallel }^2+2\text{Re}〈y,j(x+y)〉.$$

Main results

Now, we prove our main results.

Theorem 9

Let K be a nonempty closed convex subset of an arbitrary Banach space X and let T : K→K be a uniformly continuous and ϕ -hemicontractive mapping. Suppose that${\left\{u_n\right\}}_{n=1}^{\infty }$is a bounded sequence in K and${\left\{a_n^{\prime }\right\}}_{n=1}^{\infty }$, ${\left\{b_n^{\prime }\right\}}_{n=1}^{\infty }$, and${\left\{c_n^{\prime }\right\}}_{n=1}^{\infty }$are sequences in [0,1] satisfying conditions (i)$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1,$(ii)$\underset{n\to \infty }{lim}{b}_n^{\prime }=0$, (iii)$c_n^{\prime }=o\left(b_n^{\prime }\right)$, and (iv)$\sum _{n=1}^{\infty }{b}_n^{\prime }=\infty$. For a sequence${\left\{v_n\right\}}_{n=1}^{\infty }$in K, suppose that${\left\{x_n\right\}}_{n=1}^{\infty }$is the sequence generated from an arbitrary x₀∈K by

$$x_n=a_n^{\prime }{x}_{n-1}+b_n^{\prime }T{v}_n+c_n^{\prime }{u}_n,n\ge 1,$$

(3.1)

and satisfying $\underset{n\to \infty }{lim}\parallel v_n-x_n\parallel =0.$ Then, the following conditions are equivalent:

(a)${\left\{x_n\right\}}_{n=1}^{\infty }$converges strongly to the unique fixed point q of T,

(b) ${\left\{T{x}_n\right\}}_{n=1}^{\infty }$ is bounded.

Proof

From (iii), we have $c_n^{\prime }=t_n{b}_n^{\prime }$, where t _n →0 as n→∞.

Since T is ϕ-hemicontractive, it follows that F(T) is a singleton. Let F(T)={q} for some q∈K.

Suppose that $\underset{n\to \infty }{lim}{x}_n=q$, then the uniform continuity of T yields that

$$\underset{n\to \infty }{lim}T{x}_n=\mathrm{q.}$$

Therefore, ${\left\{T{x}_n\right\}}_{n=1}^{\infty }$ is bounded.

Note that $\underset{n\to \infty }{lim}\parallel v_n-x_n\parallel =0$ and the continuity of T imply that

$$\underset{n\to \infty }{lim}\parallel T{v}_n-T{x}_n\parallel =0.$$

(3.2)

Put

$$\begin{array}{ll}{M}_1=& \parallel x_0-q\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel u_n-q\parallel \\ +\underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel .\end{array}$$

(3.3)

It is clear that ||x₀−q||≤M₁. Let ||x_n−1−q||≤M₁. Next, we will prove that ||x _n −q||≤M₁.

Consider

$$\begin{array}{ll}\parallel x_n-q\parallel & =∥a_n^{\prime }{x}_{n-1}+b_n^{\prime }T{v}_n+c_n^{\prime }{u}_n-q∥\\ =∥a_n^{\prime }(x_{n-1}-q)+b_n^{\prime }(T{v}_n-q)+c_n^{\prime }(u_n-q)∥\\ \le \left(1-b_n^{\prime }\right)\parallel x_{n-1}-q\parallel +b_n^{\prime }\parallel T{v}_n-q\parallel +c_n^{\prime }\parallel u_n-q\parallel \\ \le \left(1-b_n^{\prime }\right)M_1+b_n^{\prime }(\parallel T{v}_n-T{x}_n\parallel +\parallel T{x}_n-q\parallel )\\ +c_n^{\prime }\parallel u_n-q\parallel \\ =\left(1-b_n^{\prime }\right)\left[\parallel x_0-q\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel \right.\\ \left.+\underset{n\ge 1}{sup}\parallel u_n-q\parallel +\underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel \right]\\ +b_n^{\prime }(\parallel T{v}_n-T{x}_n\parallel +\parallel T{x}_n-q\parallel )+c_n^{\prime }\parallel u_n-q\parallel \\ \le \parallel x_0-q\parallel \\ +\left(\left(1-b_n^{\prime }\right)\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +b_n^{\prime }\parallel T{x}_n-q\parallel \right)\\ +\left(\left(1-b_n^{\prime }\right)\underset{n\ge 1}{sup}\parallel u_n-q\parallel +b_n^{\prime }\parallel u_n-q\parallel \right)\\ +\left(\left(1-b_n^{\prime }\right)\underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel +b_n^{\prime }\parallel T{v}_n-T{x}_n\parallel \right)\\ \le \parallel x_0-q\parallel \\ +\left(\left(1-b_n^{\prime }\right)\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +b_n^{\prime }\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel \right)\\ +\left(\left(1-b_n^{\prime }\right)\underset{n\ge 1}{sup}\parallel u_n-q\parallel +b_n^{\prime }\underset{n\ge 1}{sup}\parallel u_n-q\parallel \right)\\ +\left(\left(1-b_n^{\prime }\right)\underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel +b_n^{\prime }\underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel \right)\\ =\parallel x_0-q\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel u_n-q\parallel \\ +\underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel \\ =M_1.\end{array}$$

So, from the above discussion, we can conclude that the sequence {x _n −q}_n≥1 is bounded. Thus, there is a constant M>0 satisfying

$$\begin{array}{ll}M=& \underset{n\ge 1}{sup}\parallel x_n-q\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel +\underset{n\ge 1}{sup}\parallel u_n-q\parallel \\ +\underset{n\ge 1}{sup}∥T{v}_n-T{x}_n∥.\end{array}$$

(3.4)

Obviously, M<∞. Consider

$$\begin{array}{ll}\parallel T{v}_n-q\parallel & \le \parallel T{v}_n-T{x}_n\parallel +\parallel T{x}_n-q\parallel \\ \le \underset{n\ge 1}{sup}\parallel T{v}_n-T{x}_n\parallel +\underset{n\ge 1}{sup}\parallel T{x}_n-q\parallel \\ \le \mathrm{M.}\end{array}$$

(3.5)

By virtue of Lemma 4 and (3.1), we infer that

$$\begin{array}{ll}\parallel x_n-q{\parallel }^2& ={∥a_n^{\prime }{x}_{n-1}+b_n^{\prime }T{v}_n+c_n^{\prime }{u}_n-q∥}^2\\ ={∥a_n^{\prime }(x_{n-1}-q)+b_n^{\prime }(T{v}_n-q)+c_n^{\prime }(u_n-q)∥}^2\\ \le {\left(1-b_n^{\prime }\right)}^2\parallel x_{n-1}-q{\parallel }^2+2b_n^{\prime }\text{Re}〈T{v}_n-q,j(x_n-q)〉\\ +2c_n^{\prime }\text{Re}〈u_n-q,j(x_n-q)〉\\ \le {\left(1-b_n^{\prime }\right)}^2\parallel x_{n-1}-q{\parallel }^2+2b_n^{\prime }\text{Re}〈T{v}_n-T{x}_n,j(x_n-q)〉\\ +2b_n^{\prime }\text{Re}〈T{x}_n-q,j(x_n-q)〉+2c_n^{\prime }\parallel u_n-q\parallel \parallel x_n-q\parallel \\ \le {\left(1-b_n^{\prime }\right)}^2\parallel x_{n-1}-q{\parallel }^2+2b_n^{\prime }\parallel T{v}_n-T{x}_n\parallel \parallel x_n-q\parallel \\ +2b_n^{\prime }\parallel x_n-q{\parallel }^2-2b_n^{\prime }\varphi (\parallel x_n-q\parallel )\parallel x_n-q\parallel +2M^2{c}_n^{\prime }\\ ={\left(1-b_n^{\prime }\right)}^2\parallel x_{n-1}-q{\parallel }^2+2M{b}_n^{\prime }{w}_n+2b_n^{\prime }\parallel x_n-q{\parallel }^2\\ -2b_n^{\prime }\varphi (\parallel x_n-q\parallel )\parallel x_n-q\parallel +2M^2{c}_n^{\prime },\end{array}$$

(3.6)

where

$$w_n=\parallel T{v}_n-T{x}_n\parallel .$$

(3.7)

Consider

$$\begin{array}{ll}\parallel x_n-q{\parallel }^2& ={∥a_n^{\prime }{x}_{n-1}+b_n^{\prime }T{v}_n+c_n^{\prime }{u}_n-q∥}^2\\ ={∥a_n^{\prime }(x_{n-1}-q)+b_n^{\prime }(T{v}_n-q)+c_n^{\prime }(u_n-q)∥}^2\\ \le a_n^{\prime }\parallel x_{n-1}-q{\parallel }^2+b_n^{\prime }\parallel T{v}_n-q{\parallel }^2+c_n^{\prime }\parallel u_n-q{\parallel }^2\\ \le \parallel x_{n-1}-q{\parallel }^2+M^2\left(b_n^{\prime }+c_n^{\prime }\right),\end{array}$$

(3.8)

where the first inequality holds by the convexity of ∥.∥².

Substituting (3.8) in (3.6), we get

$$\begin{array}{ll}\parallel x_n-q{\parallel }^2& \le \left[{\left(1-b_n^{\prime }\right)}^2+2b_n^{\prime }\right]\parallel x_{n-1}-q{\parallel }^2\\ +2M{b}_n^{\prime }\left(w_n+M\left(b_n^{\prime }+2t_n\right)\right)\\ -2b_n^{\prime }\varphi (\parallel x_n-q\parallel )\parallel x_n-q\parallel \\ =\left(1+b_n^{{\prime }^2}\right)\parallel x_{n-1}-q{\parallel }^2\\ +2M{b}_n^{\prime }\left(w_n+M{b}_n^{\prime }+2t_n\right))\\ -2b_n^{\prime }\varphi (\parallel x_n-q\parallel )\parallel x_n-q\parallel \\ \le \parallel x_{n-1}-q{\parallel }^2\\ +M{b}_n^{\prime }\left(3M{b}_n^{\prime }+2(w_n+2M{t}_n)\right)\\ -2b_n^{\prime }\varphi (\parallel x_n-q\parallel )\parallel x_n-q\parallel \\ =\parallel x_{n-1}-q{\parallel }^2+b_n^{\prime }{l}_n\\ -2b_n^{\prime }\varphi (\parallel x_n-q\parallel )\parallel x_n-q\parallel ,\end{array}$$

(3.9)

where

$$l_n=M\left(3M{b}_n^{\prime }+2\left(w_n+2M{t}_n\right)\right)\to 0,$$

(3.10)

as n→∞.

Let δ = inf{∥x_n+1−q∥:n≥0}. We claim that δ=0. Otherwise δ>0. Thus, (3.10) implies that there exists a positive integer N₁>N₀ such that l _n <ϕ(δ)δ for each n≥N₁. In view of (3.9), we conclude that

$$\parallel x_{n+1}-q{\parallel }^2\le \parallel x_n-q{\parallel }^2-\varphi \left(\delta \right)\delta b_n^{\prime },n\ge N_1,$$

which implies that

$$\varphi \left(\delta \right)\delta \sum _{n=N_1}^{\infty }{b}_n^{\prime }\le \parallel x_{N_1}-q{\parallel }^2,$$

(3.11)

which contradicts (i v). Therefore, δ=0. Thus, there exists a subsequence ${\left\{x_{n_i+1}\right\}}_{n=0}^{\infty }$ of ${\left\{x_{n+1}\right\}}_{n=0}^{\infty }$ such that

$$\underset{i\to \infty }{lim}{x}_{n_i+1}=\mathrm{q.}$$

(3.12)

Let ε>0 be a fixed number. By virtue of (3.10) and (3.12), we can select a positive integer i₀>N₁ such that

$$∥x_{n_{i_0}+1}-q∥<\epsilon ,l_n<\varphi \left(\epsilon \right)\epsilon ,n\ge n_{i_0}.$$

(3.13)

Let $p=n_{i_0}$. By induction, we show that

$$\parallel x_{p+m}-q\parallel <\epsilon ,m\ge 1.$$

(3.14)

Observe that (3.13) means that (3.14) is true for m=1. Suppose that (3.14) is true for some m≥1. If ∥x_p+m+1−q∥≥ε, by (3.9) and (3.13), we know that

$$\begin{array}{ll}{\epsilon }^2& \le \parallel x_{p+m+1}-q{\parallel }^2\\ \le \parallel x_{p+m}-q{\parallel }^2+\frac{b_{p+m}^{\prime }{l}_{p+m}}{1-2b_{p+m}^{\prime }}\\ -\frac{2b_{p+m}^{\prime }}{1-2b_{p+m}^{\prime }}\varphi (\parallel x_{p+m+1}-q\parallel )\parallel x_{p+m+1}-q\parallel \\ <{\epsilon }^2+\frac{b_{p+m}^{\prime }\varphi \left(\epsilon \right)\epsilon }{1-2b_{p+m}^{\prime }}-\frac{2b_{p+m}^{\prime }\varphi \left(\epsilon \right)\epsilon }{1-2b_{p+m}^{\prime }}\\ <{\epsilon }^2,\end{array}$$

which is impossible. Hence, ∥x_p+m+1−q∥<ε. That is, (3.14) holds for all m≥1. Thus, (3.14) ensures that $\underset{n\to \infty }{lim}{x}_n=q$. This completes the proof. □

Using the method of proofs in Theorem 6, we have the following result:

Theorem 10

Let$X,K,T,{\left\{u_n\right\}}_{n=1}^{\infty },{\left\{v_n\right\}}_{n=1}^{\infty }$, and${\left\{x_n\right\}}_{n=1}^{\infty }$be as in Theorem 9. Suppose that${\left\{a_n^{\prime }\right\}}_{n=1}^{\infty },{\left\{b_n^{\prime }\right\}}_{n=1}^{\infty }$, and${\left\{c_n^{\prime }\right\}}_{n=1}^{\infty }$are sequences in [0,1] satisfying conditions (i), (i i), (i v), and

$$\sum _{n=1}^{\infty }{c}_n^{\prime }<\mathrm{\infty .}$$

Then, the conclusion of Theorem 9 holds.

Corollary 11

Let K be a nonempty closed convex subset of an arbitrary Banach space X and let T: K→K be a uniformly continuous and ϕ -hemicontractive mapping. Suppose that${\left\{u_n\right\}}_{n=1}^{\infty }$is a bounded sequence in K, and${\left\{a_n^{\prime }\right\}}_{n=1}^{\infty }$, ${\left\{b_n^{\prime }\right\}}_{n=1}^{\infty }$, and${\left\{c_n^{\prime }\right\}}_{n=1}^{\infty }$are sequences in [0,1] satisfying conditions (i)$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1,$(ii)$\underset{n\to \infty }{lim}{b}_n^{\prime }=0$, (iii)$c_n^{\prime }=0\left(b_n^{\prime }\right)$, and (iv)$\sum _{n=1}^{\infty }{b}_n^{\prime }=\infty$. Suppose that${\left\{x_n\right\}}_{n=1}^{\infty }$is the sequence generated from an arbitrary x₀∈K by

$$x_n=a_n^{\prime }{x}_{n-1}+b_n^{\prime }T{x}_n+c_n^{\prime }{u}_n,n\ge 1.$$

Then, the following conditions are equivalent:

(a)${\left\{x_n\right\}}_{n=1}^{\infty }$converges strongly to the unique fixed point q of T,

(b) ${\left\{T{x}_n\right\}}_{n=1}^{\infty }$ is bounded.

Corollary 12

Let$X,K,T,{\left\{u_n\right\}}_{n=1}^{\infty }$, and${\left\{x_n\right\}}_{n=1}^{\infty }$be as in Corollary 11. Suppose that${\left\{a_n^{\prime }\right\}}_{n=1}^{\infty },{\left\{b_n^{\prime }\right\}}_{n=1}^{\infty }$, and${\left\{c_n^{\prime }\right\}}_{n=1}^{\infty }$are sequences in [0,1] satisfying conditions (i), (i i), (i v) and

$$\sum _{n=1}^{\infty }{c}_n^{\prime }<\mathrm{\infty .}$$

Then, the conclusion of Corollary 12 holds.

Corollary 13

Let K be a nonempty closed convex subset of an arbitrary Banach space X and let T: K→K be a uniformly continuous and ϕ -hemicontractive mapping. Suppose that${\left\{{\alpha }_n\right\}}_{n=1}^{\infty }$be any sequence in [0,1] satisfying (i)$\underset{n\to \infty }{lim}{\alpha }_n=0$and (ii)$\sum _{n=1}^{\infty }{\alpha }_n=\infty$. For a sequence${\left\{v_n\right\}}_{n=1}^{\infty }$in K, suppose that${\left\{x_n\right\}}_{n=1}^{\infty }$is the sequence generated from an arbitrary x₀∈K by

$$x_n={\alpha }_n{x}_{n-1}+(1-{\alpha }_n)T{v}_n,n\ge 1$$

and satisfying$\underset{n\to \infty }{lim}\parallel v_n-x_n\parallel =0$. Then, the following conditions are equivalent:

(a)${\left\{x_n\right\}}_{n=1}^{\infty }$converges strongly to the unique fixed point q of T,

(b) ${\left\{T{x}_n\right\}}_{n=1}^{\infty }$ is bounded.

Corollary 14

Let K be a nonempty closed convex subset of an arbitrary Banach space X and let T: K→K be a uniformly continuous and ϕ -hemicontractive mapping. Suppose that${\left\{{\alpha }_n\right\}}_{n=1}^{\infty }$be any sequence in [0,1] satisfying (i)$\underset{n\to \infty }{lim}{\alpha }_n=0$and (ii)$\sum _{n=1}^{\infty }{\alpha }_n=\infty$. For any x _o ∈K, define the sequence${\left\{x_n\right\}}_{n=1}^{\infty }$inductively as follows:

$$x_n={\alpha }_n{x}_{n-1}+(1-{\alpha }_n)T{x}_n,n\ge 1.$$

Then the following conditions are equivalent:

(a)${\left\{x_n\right\}}_{n=1}^{\infty }$converges strongly to the unique fixed point q of T,

(b) ${\left\{T{x}_n\right\}}_{n=1}^{\infty }$ is bounded.

Remark 15

All of the above results are also valid for Lipschitz ϕ-hemicontractive mappings.

Multi-step implicit fixed point iterations

Let K be a nonempty closed convex subset of a real normed space X and T₁,T₂,…,T _p :K→K(p≥2) be a family of self-mappings.

Algorithm 1

For a given x₀∈K, compute the sequence {x _n } by the implicit iteration process of arbitrary fixed order p≥2,

$$\begin{array}{rl}{x}_n& =a_n^{\prime }{x}_{n-1}+b_n^{\prime }{T}_1{y}_n^1+c_n^{\prime }{u}_n,\\ y_n^i& =a_n^i{x}_{n-1}+b_n^i{T}_{i+1}{y}_n^{i+1}+c_n^i{v}_n^i;i=1,2,\dots ,p-2,\\ y_n^{p-1}& =a_n^{p-1}{x}_{n-1}+b_n^{p-1}{T}_p{x}_n+c_n^{p-1}{v}_n^{p-1},n\ge 0,\end{array}$$

(4.1)

which is called the multi-step implicit iteration process, where {a _n }, $\left\{b_n\right\},\left\{c_n\right\},\left\{a_n^i\right\},\left\{b_n^i\right\}$, $\left\{c_n^i\right\}\subset [0,1]$;$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1=a_n^i+b_n^i+c_n^i;$and {u _n } and$\left\{v_n^i\right\}$are arbitrary sequences in K provided i=1,2,…,p−1.

For p=3, we obtain the following three-step implicit iteration process:

Algorithm 2

For a given x₀∈K, compute the sequence {x _n } by the iteration process

$$\begin{array}{ll}{x}_n& =a_n^{\prime }{x}_{n-1}+b_n^{\prime }{T}_1{y}_n^1+c_n^{\prime }{u}_n,\\ y_n^1& =a_n^1{x}_{n-1}+b_n^1{T}_2{y}_n^2+c_n^1{v}_n^1,\\ y_n^2& =a_n^2{x}_{n-1}+b_n^2{T}_3{x}_n+c_n^2{v}_n^2,n\ge 0,\end{array}$$

(4.2)

where$\left\{a_n^{\prime }\right\}$, $\left\{b_n^{\prime }\right\},\left\{c_n^{\prime }\right\},\left\{a_n^i\right\}$, $\left\{b_n^i\right\},\left\{c_n^i\right\}\subset [0,1]$;$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1=a_n^i+b_n^i+c_n^i$; and {u _n } and$\left\{v_n^i\right\}$are arbitrary sequences in K provided i=1, 2.

For p=2, we obtain the following two-step implicit iteration process:

Algorithm 3

For a given x₀∈K, compute the sequence {x _n } by the iteration process

$$\begin{array}{ll}{x}_n& =a_n^{\prime }{x}_{n-1}+b_n^{\prime }{T}_1{y}_n^1+c_n^{\prime }{u}_n,\\ y_n^1& =a_n^1{x}_{n-1}+b_n^1{T}_2{x}_n+c_n^1{v}_n^1,n\ge 0,\end{array}$$

(4.3)

where$\left\{a_n^{\prime }\right\}$, $\left\{b_n^{\prime }\right\},\left\{c_n^{\prime }\right\},\left\{a_n^1\right\},\left\{b_n^1\right\}$, $\left\{c_n^1\right\}\subset [0,1]$;$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1=a_n^1+b_n^1+c_n^1$; and {u _n } and$\left\{v_n^1\right\}$are arbitrary sequences in K.

If $T_1=T,T_2=I,b_n^1=1$, and $c_n^1=0$ in (4.3), we obtain the implicit Mann iteration process:

Algorithm 4

[2]For any given x₀∈K, compute the sequence {x _n } by the iteration process

$$x_n=a_n^{\prime }{x}_{n-1}+b_n^{\prime }T{x}_n+c_n^{\prime }{u}_n,n\ge 0,$$

(4.4)

where$\left\{a_n^{\prime }\right\}$, $\left\{b_n^{\prime }\right\},\left\{c_n^{\prime }\right\}\subset [0,1]$;$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1$; and {u _n } is an arbitrary sequence in K.

Theorem 16

Let K be a nonempty closed convex subset of an arbitrary Banach space X and T₁,T₂,…,T _p (p≥2) be self-mappings of K. Let T₁be a continuous ϕ -hemicontractive mapping and R(T₂) is bounded. Let$\left\{a_n^{\prime }\right\}$, $\left\{b_n^{\prime }\right\}$, $\left\{c_n^{\prime }\right\}$, $\left\{a_n^i\right\}$, $\left\{b_n^i\right\}$, $\left\{c_n^i\right\}$be real sequences in [0,1];$a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1=a_n^i+b_n^i+c_n^i$, i=1,2,…,p−1 satisfying (i)$\underset{n\to \infty }{lim}{b}_n^{\prime }=0$, (ii)$c_n^{\prime }=0\left(b_n^{\prime }\right)$, and (iii)$\sum _{n=1}^{\infty }{b}_n^{\prime }=\infty$, $\underset{n\to \infty }{lim}{b}_n^1=0=\underset{n\to \infty }{lim}{c}_n^1$. For arbitrary x₀∈K, define the sequence {x _n } by (4.1). Then, {x _n } converges strongly to the common fixed point of$\bigcap _{i=1}^{p}F\left(T_i\right)\ne \varnothing$.

Proof

By applying Theorem 9 under the assumption that T₁ is continuous ϕ- hemicontractive, we obtain Theorem 16 which proves strong convergence of the iteration process defined by (4.1). Consider the following estimates by taking T₁=T and $v_n=y_n^1,$

$$\parallel v_n-x_n\parallel \le \parallel v_n-x_{n-1}\parallel +\parallel x_{n-1}-x_n\parallel ,$$

(4.5)

$$\begin{array}{ll}\parallel v_n-x_{n-1}\parallel & =∥a_n^1{x}_{n-1}+b_n^1{T}_2{y}_n^2+c_n^1{v}_n^1-x_{n-1}∥\\ =∥b_n^1\left(T_2{y}_n^2-x_{n-1}\right)+c_n^1\left(v_n^1-x_{n-1}\right)∥\\ \le b_n^1∥T_2{y}_n^2-x_{n-1}∥+c_n^1∥v_n^1-x_{n-1}∥\\ \le 2M\left(b_n^1+c_n^1\right),\end{array}$$

(4.6)

$$\begin{array}{ll}\parallel x_{n-1}-x_n\parallel & =∥x_{n-1}-a_n^{\prime }{x}_{n-1}-b_n^{\prime }T{v}_n-c_n^{\prime }{u}_n∥\\ =∥b_n^{\prime }(x_{n-1}-T{v}_n)-c_n^{\prime }(u_n-x_{n-1})∥\\ \le b_n^{\prime }\parallel x_{n-1}-T{v}_n\parallel +c_n^{\prime }\parallel u_n-x_{n-1}\parallel \\ \le 2M(b_n^{\prime }+c_n^{\prime }).\end{array}$$

(4.7)

Substituting (4.6 to 4.7) in (4.5), we have

$$\begin{array}{ll}\parallel v_n-x_n\parallel & \le 2M(b_n^1+c_n^1+b_n^{\prime }+c_n^{\prime })\\ \to 0,\end{array}$$

as n→∞. □

Corollary 17

Let K be a nonempty closed convex subset of an arbitrary Banach space X and T₁,T₂,…,T _p (p≥2) be self-mappings of K. Let T₁be a Lipschitz ϕ -hemicontractive mapping, and R(T₂) is bounded. Let$\left\{a_n^{\prime }\right\}$, $\left\{b_n^{\prime }\right\}$, $\left\{c_n^{\prime }\right\}$, $\left\{a_n^i\right\}$, $\left\{b_n^i\right\}$, and$\left\{c_n^i\right\}$be real sequences in$[0,1];a_n^{\prime }+b_n^{\prime }+c_n^{\prime }=1=a_n^i+b_n^i+c_n^i$, i=1,2,…,p−1 satisfying (i)$\underset{n\to \infty }{lim}{b}_n^{\prime }=0$, (ii)$c_n^{\prime }=0\left(b_n^{\prime }\right)$, and (iii)$\sum _{n=1}^{\infty }{b}_n^{\prime }=\infty$, $\underset{n\to \infty }{lim}{b}_n^1=0=\underset{n\to \infty }{lim}{c}_n^1$. For arbitrary x₀∈K, define the sequence {x _n } by (4.1). Then, {x _n } converges strongly to the common fixed point of$\bigcap _{i=1}^{p}F\left(T_i\right)\ne \varnothing$.