Characterizations involving Schwarzian derivative in some analytic function spaces

Abstract

In this paper, for conformal mapping f, we study the membership of logf^′ to the ${\mathcal{Q}}_K(p,q)$)-type spaces of analytic functions. Moreover, geometric conditions and some important characterizations involving the Schwarzian derivative are also given.

AMS 2010 classification

30D45; 46E15

Introduction

Let $\mathbb{D}=\{zϵ\mathbb{C}:|z|<1\}$ be the open unit disk of the complex plane $\mathbb{C}$.$\mathcal{H}(\mathbb{D})$ denotes the space of all analytic functions in $\mathbb{D}$, and d A(z) is the normalized area measure on $\mathbb{D}$ so that

$$A(\mathbb{D})\equiv 1.$$

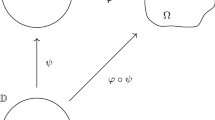
Let Green’s function of $\mathbb{D}$ be defined as $g(z,a)=\text{log}\frac{1}{|{\phi }_a(z)|}$, where ${\phi }_a(z)=\frac{z-a}{1-āz}$, for $z,aϵ\mathbb{D}$ is the Möbius transformation related to the point $aϵ\mathbb{D.}$ A complex-valued function defined in $\mathbb{D}$ is said to be univalent if it is analytic and one-to-one there.The class of all univalent functions in $\mathbb{D}$ will be denoted by $\mathcal{U}.$ If $fϵ\mathcal{U}$, $\mathrm{\Omega }=f(\mathbb{D})$, and ∂ Ω is a Jordan curve, then $f:\mathbb{D}\to \mathrm{\Omega }$ is said to be a conformal mapping, and so Ω is a simply connected domain strictly contained in $\mathbb{C}.$

For 0 < α < ∞, we say that an analytic function f on $\mathbb{D}$ belongs to the space ${\mathcal{B}}^{\alpha }$ (see [1]) if

$$\begin{array}{l}\parallel f{\parallel }_{{\mathcal{B}}^{\alpha }}=\underset{zϵ\mathbb{D}}{\text{sup}}{(1-|z{|}^2)}^{\alpha }|f^{\prime }(z)|<\infty .\end{array}$$

Moreover, we say that $fϵ{\mathcal{B}}^{\alpha }$ belongs to the space ${\mathcal{B}}_0^{\alpha }$ if

$$\begin{array}{l}\underset{|a|\to 1}{\text{lim}}{(1-|z{|}^2)}^{\alpha }|f^{\prime }(z)|=0.\end{array}$$

The space ${\mathcal{B}}^{\alpha }$ is a Banach space under the norm $\parallel f\parallel =|f(0)+\parallel f{\parallel }_{{\mathcal{B}}^{\alpha }}.$ If α = 1, the space ${\mathcal{B}}^1$ is the Bloch space $\mathcal{B}$ and the space ${\mathcal{B}}_0^1$ is the little Bloch space ${\mathcal{B}}_0$ (see [2]).

Let K : [0,∞) → [0,∞)be a right-continuous and nondecreasing function. For 0 < p < ∞,-2 < q < ∞, the space ${\mathcal{Q}}_K(p,q)$ consists of all functions $fϵ\mathcal{H}(\mathbb{D})$ (see [3]), for which

$$\begin{array}{l}\parallel f{\parallel }_{{\mathcal{Q}}_K(p,q)}^p=\underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}|f^{\prime }(z){|}^p{(1-|z{|}^2)}^{q}K(g(z,a))\mathit{\text{dA}}(z)<\infty .\end{array}$$

Moreover, we say that $fϵ{\mathcal{Q}}_K(p,q)$ belongs to the space ${\mathcal{Q}}_{K,0}(p,q)$ if

$$\begin{array}{l}\underset{|a|\to 1}{\text{lim}}{\int }_{\mathbb{D}}|f^{\prime }(z){|}^p{(1-|z{|}^2)}^{q}K(g(z,a))\mathit{\text{dA}}(z)=0.\end{array}$$

The definition of ${\mathcal{Q}}_K(p,q)$ here is based on K (g(z,a)). There is a slightly different definition of ${\mathcal{Q}}_K(p,q)$ in the literature that is based on K (1 - |φ _a (z)|²). However, it has been known that the two definitions are essentially equivalent (see [4, 5]). Equipped with the norm $|f(0)|+\parallel f{\parallel }_{{\mathcal{Q}}_K(p,q)}$, the space ${\mathcal{Q}}_K(p,q)$ is a Banach space when p ≥ 1. If q + 2 = p, ${\mathcal{Q}}_K(p,q)$ is Möbius-invariant, i.e.,

$$\parallel f\circ {\phi }_a{\parallel }_{{\mathcal{Q}}_K(p,q)}=\parallel f{\parallel }_{{\mathcal{Q}}_K(p,q)}$$

for all $aϵ\mathbb{D.}$ The study of ${\mathcal{Q}}_K(p,q)$ space has mainly been on understanding the relationship between the properties of K and the resulting spaces ${\mathcal{Q}}_K(p,q).$ For more information about these spaces, we refer to [3, 6–9].

Let $fϵ\mathcal{U}.$ For a Banach space $X\subset \mathcal{H}(\mathbb{D})$, we say that $\mathrm{\Omega }=f(\mathbb{D})$ is an X-domain whenever logf^′ ϵ X. Many such domains have been characterized in terms of the Schwarzian derivative of a conformal map of $\mathbb{D.}$ Namely, Becker and Pommerenke in 1978 characterized bounded ${\mathcal{B}}_0$ domains (see [10]), and in 1991, Astal and Zinsmeister gave a description of BMOA domains (see [11]). Also, Q _p  domains were characterized by Pau and Peláez in 2009 (see [12]) by using a method developed in 1994 by Bishop and Jones (see [13]). Moreover, F (p,q,s) domains were characterized by Zorboska in 2011 (see [14]).

The logarithm of the Schwarzian derivative of a univalent function plays an important role in geometric function theory in the characterization of different types of domains, and in its connections with the Teichmüller theory. For example, one of the famous results in geometric function theory by Astala and Gehring states that $\mathrm{\Omega }=f(\mathbb{D})$ is a quasi-disk, i.e., f has a quasiconformal extension to the complex plane if and only if logf^′ belongs to one of the models of a Teichmüller space $T(1)=\{\text{log}{f}^{\prime }:f\text{has a quasiconformal extension to}\mathbb{D}\}$, that is, the Bloch norm interior of the set of all mappings logf^′, with univalent function f (see [15]).

Analogously, $fϵ\mathcal{H}(\mathbb{D})$ is called locally univalent if it is injective in a neighborhood of each point of $\mathbb{D}$, which is further equivalent to f^′ (z) ≠ 0. The Schwarzian derivative of a locally univalent function was introduced by Chuaqui and Osgood in [16].

In this paper we study the membership of logf^′ to the general ${\mathcal{Q}}_K$-type spaces ${\mathcal{Q}}_K(p,q)$ in terms of Carleson measures involving the Schwarzian derivative of f. Moreover, we have given Schwarzian derivative characterizations of the spaces $S_X=\{\text{log}{f}^{\prime }:fϵ\mathcal{U},\text{log}{f}^{\prime }ϵX\}$, where X is either a ${\mathcal{Q}}_K(p,q)$ or ${\mathcal{Q}}_{K,0}(p,q)$ space, contained in the Bloch space.

Note that the space ${\mathcal{Q}}_K(p,q)$ includes the space BMOA (the space of functions analytic on $\mathbb{D}$ and with bounded mean oscillation on the unit circle), the class of so-called Q _s  space, the class of (analytic) Besov spaces B _p , and the general Besov-type spaces F (p,q,s). Thus, the results are generalizations of the recent results due to Pau and Peláez [12], Pérez-González and Rättyä [17], and Zorboska [14].

The letter C denotes a positive constant throughout the paper which may vary at each occurrence. Throughout this paper, we suppose that the nondecreasing function K is differentiable and satisfies K (2t) ≈ K(t), that is, there exist constants C₁ and C₂ such that C₁K (2t) ≤ K(t) ≤ C₂K(2t). Also, we assume that

$${\int }_0^1{(1-r^2)}^{q}K\left(\text{log}1/r\right)\mathit{\text{rdr}}<\infty .$$

(1)

Otherwise, ${\mathcal{Q}}_K(p,q)$ is trivial, that is, ${\mathcal{Q}}_K(p,q)$ contains constant functions only (see [8]). We know that ${\mathcal{Q}}_{K_1}(p,q)={\mathcal{Q}}_{K_2}(p,q)$ for K₂ = inf(K₁(r),K₁(1)) (see [8], Theorem 3.1), and so the function K can be assumed to be bounded. We know that ${\mathcal{Q}}_K(p,q)\subset {\mathcal{B}}^{\frac{q+2}{p}}$ and ${\mathcal{Q}}_{K,0}(p,q)\subset {\mathcal{B}}_0^{\frac{q+2}{p}}$ (see [8]). Also, if

$$\begin{array}{l}{\int }_0^1{(1-r^2)}^{-2}K\left(\text{log}1/r\right)\mathit{\text{rdr}}<\infty ,\end{array}$$

then ${\mathcal{Q}}_K(p,q)={\mathcal{B}}^{\frac{q+2}{p}}$ and ${\mathcal{Q}}_{K,0}(p,q)={\mathcal{B}}_0^{\frac{q+2}{p}}$ (see [8]). In order to obtain our main results in this paper, we define an auxiliary function ϕ _K  as follows:

$$\begin{array}{l}{\varphi }_K(s)=\underset{0<t<1}{\text{sup}}\frac{K(\mathit{\text{st}})}{K(t)},0<s<\infty .\end{array}$$

The following conditions play important roles in the study of ${\mathcal{Q}}_K(p,q)$ space (see [3, 8, 18]):

$${\int }_0^1{\varphi }_K(s)\frac{\mathit{\text{ds}}}{s}<\infty$$

(2)

and that

$$\underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}\frac{{(1-|z{|}^2)}^{p-2}}{|1-āz{|}^p}K\left(\text{log}\frac{1}{|z|}\right)\mathit{\text{dA}}(z)<\infty .$$

(3)

We know that (2) implies (3) for 1 < p < ∞ (see [3]).

Throughout this paper, f(z) will be a conformal mapping, and we shall write h(z) =: log(f^′)(z). We denote by P _f (z) the so-called pre-Schwarzian of f(z), i.e.,

$$\begin{array}{l}{P}_f(z)=:h^{\prime }(z)=\frac{f^{\mathrm{\prime \prime }}(z)}{f^{\prime }(z)}.\end{array}$$

The Schwarzian derivative of a locally univalent function f is

$$S_f(z)=P_f^{\prime }(z)-\frac{1}{2}{\left(P_f(z)\right)}^2={\left(\frac{f^{\mathrm{\prime \prime }}(z)}{f^{\prime }(z)}\right)}^{\prime }-\frac{1}{2}{\left(\frac{f^{\mathrm{\prime \prime }}(z)}{f^{\prime }(z)}\right)}^2.$$

(4)

We list few properties of P _f (z) and S _f (z). For proofs and more details, see [19].

• (A) If f is univalent on $\mathbb{D},$ then (1 - |z|²)|P _f (z)| ≤ 6 and (1 - |z|²)²|S _f (z)| ≤ 6.

• (B) If (1 - |z|²)|z P _f (z)| ≤ 1 or (1 - |z|²)²|S _f (z)| ≤ 2, then f is univalent on $\mathbb{D.}$

• (C) For $hϵH(\mathbb{D}),hϵ\mathcal{B}$ if and only if there exist $wϵ\mathbb{C}$ and a univalent f such that h = w logf ^′.

• (D) The Schwarzian derivative is Möbius-invariant in the sense that $S_{{\phi }_a\circ f}=S_f$, and it is also such that ${(1-|z{|}^2)}^2|S_{f\circ {\phi }_a}(z)|={(1-|{\phi }_a(z){|}^2)}^2|S_f({\phi }_a(z))|$, for every Möbius transformation ${\phi }_a(z)),aϵ\mathbb{D.}$

For a subarc $I\subset \partial \mathbb{D}$, the boundary of $\mathbb{D}$, let

$$\begin{array}{l}S(I)=\{\mathrm{r\zeta }ϵ\mathbb{D}:1-|I|<r<1,\zeta ϵI\}.\end{array}$$

If |I| ≥ 1, then we set $S(I)=\mathbb{D.}$ A positive measure μ is said to be a bounded K -Carleson measure on $\mathbb{D}$ (see [18]) if

$$\begin{array}{l}\underset{I\subset \partial \mathbb{D}}{\text{sup}}{\int }_{S(I)}K\left(\frac{1-|z|}{|I|}\right)d\mu (z)<\infty .\end{array}$$

Moreover, if

$$\begin{array}{l}\underset{|I|\to 0}{\text{lim}}{\int }_{S(I)}K\left(\frac{1-|z|}{|I|}\right)d\mu (z)=0,\end{array}$$

then μ is a compact K -Carleson measure.

Clearly, if K (t) = t^p, then μ is a bounded p-Carleson measure on $\mathbb{D}$ if and only if (1 - |z|²)d μ is a bounded p-Carleson measure on $\mathbb{D}$ (see [18]). The following lemma is Corollary 3.2 in [18].

Lemma 1.

Let K :[0,∞) → [0,∞) satisfy (2). Then a positive measure μ on$\mathbb{D}$is a K-Carleson measure if and only if

$$\begin{array}{l}\underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}K\left(1-|{\phi }_a(z){|}^2\right)d\mu (z)<\infty .\end{array}$$

Next, for each n = 1,2,…, from the dyadic Carleson boxes

$$\begin{array}{ll}{Q}_{n,j}& =\left\{z=r{e}^{\mathit{i\theta }}ϵ\mathbb{D}:1-\frac{1}{2^n}\le |z|<1,\frac{j}{2^{n+1}}\right.\\ \le \left.\frac{\theta }{\pi }<\frac{j+1}{2^{n+1}}\right\},0\le j\le 2^{n+1},\end{array}$$

of side-length $\ell (Q_{n,j})=\frac{1}{2^n}$ and their inner half

$$T(Q_{n,j})=Q_{n,j}\cap \{zϵQ_{n,j}:1-\frac{1}{2^n}\le |z|<\frac{1}{2}\ell (Q_{n,j})\}.$$

From [20], for a univalent function f, the given δ and ε will be determined later. If Q is a dyadic Carleson box, we shall say Q is bad if

$$\begin{array}{l}\underset{zϵT(Q)}{\text{sup}}(1-|z{|}^2)|P_f(z)|\ge \epsilon \text{and}\underset{zϵT(Q)}{\text{sup}}{(1-|z{|}^2)}^2|S_f(z)|\le \delta .\end{array}$$

We callQ a maximal bad square if the next bigger dyadic square $\tilde{Q}$ containing Q has either $\ell (\tilde{Q})=\frac{1}{2}$ or $\underset{zϵT(Q)}{\text{sup}}{(1-|z{|}^2)}^2|S_f(z)|>\delta .$

Lemma 2.

[12] Let f be a univalent function on$\mathbb{D}$, and suppose that there exists$z_0ϵ\mathbb{D}$such that |S _f (z₀)|²(1 - |z₀|²) > δ. Then there is a positive constant c = c(δ) < 1such that$|S_f(z){|}^2(1-|z{|}^2)>\frac{\delta }{32}$, whenever$zϵ\mathbb{D}(z_0,c(1-|z_0{|}^2))$.

In the proof of Theorem 4, some sums of the type $\sum _j\ell [K(Q)]$ will be estimated. One of them appears in the following lemma.

Lemma 3.

Let p,ε,δ be positive constants and K:[ 0,∞) → [ 0,∞). Then there exists C₁,C₂ > 0 such that

$$\begin{array}{l}\sum _j\ell [K(Q_j)]\le C_1\\ +C_2{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

(5)

Proof.

Let Q be a maximal square with $\ell (Q)\ne \frac{1}{2}.$ Then $\tilde{Q}$ is a maximal bad square, and hence, there exists $z_0ϵT(\tilde{Q})$ with

$$\begin{array}{l}{(1-|z{|}^2)}^2|S_f(z_0)|>\delta .\end{array}$$

Then, by Lemma 2, there is a disk ${\mathbb{D}}_{z_0}=\mathbb{D}(z_0,c(1-|z_0{|}^2))\subset T(\tilde{Q})$ such that

$$\begin{array}{l}{(1-|z{|}^2)}^2|S_f(z)|>\frac{\delta }{32},\text{for all}zϵ{\mathbb{D}}_{z_0}.\end{array}$$

Then

$$\begin{array}{ll}\ell [K(Q)]& \approx \ell [K(\tilde{Q})]\le {\int }_{{\mathbb{D}}_{z_0}}{(1-|z{|}^2)}^{-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le C{\int }_{{\mathbb{D}}_{z_0}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

Since any top half $T({\tilde{Q}}_j)$ can appear only two times, and since there are only two squares Q^′ with $\ell (Q^{\prime })=\frac{1}{2}$, then (5) holds. □

The n th derivative of ${\mathcal{Q}}_{\mathit{K}}(p,q)$space

First, we give some equivalent conditions for the n th derivative of ${\mathcal{Q}}_K(p,q)$ spaces.

Theorem 1.

Let K:[0,∞) → [0,∞) satisfy (2), (3), 0 < p < ∞ and -2< q < ∞. Suppose that n is a positive integer, and$hϵ\mathcal{H}(\mathbb{D})$. Then the following statements are equivalent:

(i) $hϵ{\mathcal{Q}}_K(p,q);$

(ii) |h⁽ⁿ⁾(z)|^p(1 - |z|²)^np-p+qd A(z) is a K-Carleson

measure;

(iii)

$$\underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}|h^{(n)}(z){|}^p{(1-|z{|}^2)}^{\mathit{\text{np}}-p+q}K(g(z,a))\mathit{\text{dA}}(z)<\infty ;$$

(iv)

$$\begin{array}{ll}\underset{aϵ\mathbb{D}}{\text{sup}}& {\int }_{\mathbb{D}}|h^{(n)}(z){|}^p{(1-|z{|}^2)}^{\mathit{\text{np}}-p+q}K\left(1-|{\phi }_a(z){|}^2\right)\\ \times \mathit{\text{dA}}(z)<\infty .\end{array}$$

Proof

(i) ⇔ (ii). This implication is an immediate consequence of the corresponding part of the proof of Theorem 2 in [3].(i) ⇔ (iii). Similarly as in the proof of Theorem 1in [3], the implication follows.(ii) ⇔ (iv). By Lemma 1for d μ(z) = |h⁽ⁿ⁾(z)|^p(1 - |z|²)^np-p+qd A(z), then μ is a K-Carleson measure if and only if

$$\begin{array}{l}\underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}K\left(1-|{\phi }_a(z){|}^2\right)d\mu (z)\\ =& \underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}|h^{(n)}(z){|}^p{(1-|z{|}^2)}^{\mathit{\text{np}}-p+q}K\left(1-|{\phi }_a(z){|}^2\right)\\ \times \mathit{\text{dA}}(z)<\infty .\end{array}$$

Thus, the implication follows. □

Theorem 1 has a corresponding ‘little-oh’ version in terms of compact K-Carleson measure as follows:

Theorem 2

Let K:[0,∞)→[0,∞) satisfy (2), (3),0 < p < ∞ and -2 < q < ∞. Suppose that n is a positive integer, and$hϵ\mathcal{H}(\mathbb{D})$. Then the following statements are equivalent:

(i) $hϵ{\mathcal{Q}}_{K,0}(p,q);$

(ii) |h⁽ⁿ⁾(z)|^p(1 - |z|²)^np-p+qd A(z) is a compact

K-Carleson measure;

(iii)

$$\underset{|a|\to 1}{\text{lim}}{\int }_{\mathbb{D}}|h^{(n)}(z){|}^p{(1-|z{|}^2)}^{\mathit{\text{np}}-p+q}K(g(z,a))\mathit{\text{dA}}(z)=0;$$

(iv)

$$\begin{array}{ll}\underset{|a|\to 1}{\text{lim}}& {\int }_{\mathbb{D}}|h^{(n)}(z){|}^p{(1-|z{|}^2)}^{\mathit{\text{np}}-p+q}K\left(1-|{\phi }_a(z){|}^2\right)\\ \times \mathit{\text{dA}}(z)=0.\end{array}$$

Now, we prove the following lemmas:

Lemma 4.

Let K:[0,∞) → [0,∞) satisfy (2), (3), 1 ≤ p < ∞ and -2 < q < ∞ with q - p ≤ -2,and let$h=\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0.$Then if |S _f (z)|^p(1 - |z|²)^p+qd A(z) is a K-Carleson measure, we get that |P _f (z)|^p(1 - |z|²)^qd A(z) is also a K-Carleson measure.

Proof

Recall that $S_f(z)=P_f^{\prime }(z)-\frac{1}{2}{\left(P_f(z)\right)}^2$, that by Theorem 1, |P _f (z)|^p(1 - |z|²)^qd A(z) is a K-Carleson measure if and only if |P f′(z)|^p(1 - |z|²)^p+qd A(z) is a K-Carleson measure, and that (1-|z|²)|P _f (z)| ≤ 6 for every $zϵ\mathbb{D.}$ Thus, for any 1 ≤ p < ∞, we have

$$\begin{array}{ll}I(a)& ={\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le 2^{p-1}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +\frac{1}{2}{\int }_{\mathbb{D}}|P_f(z){|}^{2p}{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

In what follows, we may assume that P _f  is continuous on $\overline{\mathbb{D}}$ (the closed unit disk), for if not, we can use instead the dilatations (P _f ) _r (z) = P _f (r z), and then at the end of the proof, take r → 1.

Since $h=\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0,$ for any ε > 0 there exists r _ε  such that whenever |z| > r _ε , we have |P _f (z)|(1 - |z|²) < ε,and

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f(z){|}^{2p}{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ =\underset{|z|>r_{\epsilon }}{\int }|P_f(z){|}^{2p}{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +\underset{|z|\le r_{\epsilon }}{\int }|P_f(z){|}^{2p}{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ =I_1(a)+I_2(a).\end{array}$$

Thus, for some C = C(p,q), we have

$$\begin{array}{ll}{I}_1(a)& =\underset{|z|>r_{\epsilon }}{\int }|P_f(z){|}^{2p}{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le {\epsilon }^p{\int }_{\mathbb{D}}|P_f(z){|}^p{(1-|z{|}^2)}^{q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le C{\epsilon }^p{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ =C{\epsilon }^{p}I(a).\end{array}$$

On the other hand, since q - p ≤ -2, for every $aϵ\mathbb{D}$ we have

$$\begin{array}{ll}{I}_2(a)& ={\int }_{|z|\le r_{\epsilon }}|P_f(z){|}^{2p}{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le 6^{2p}{\int }_{|z|\le r_{\epsilon }}{(1-|z{|}^2)}^{q-p}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le \frac{6^{2p}}{{(1-{r_{\epsilon }}^2)}^{p-q}}.\end{array}$$

Choose ε that is small enough such that $1-\frac{C{\epsilon }^p}{2}>0.$ Then, since

$$\begin{array}{ll}\left(1-\frac{C{\epsilon }^p}{2}\right)& I(a)\le 2^{p-1}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{p+q}\\ K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)+\frac{6^{2p}}{2{(1-{r_{\epsilon }}^2)}^{p-q}},\end{array}$$

(6)

and since |S _f (z)|^p(1 - |z|²)^p+qd A(z) is a K-Carleson measure, taking supremum over $aϵ\mathbb{D}$ on both sides of (6), we get

$$\begin{array}{l}\underset{aϵ\mathbb{D}}{\text{sup}}I(a)=\underset{aϵ\mathbb{D}}{\text{sup}}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{p+q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty .\end{array}$$

It follows by Theorem 1 that |P _f (z)|^p(1 - |z|²)^qd A(z) is also a K-Carleson measure, and the proof is completed. □

Now we give the following result.

Proposition 1

Let K:[0,∞) → [0,∞) satisfy (2), (3), 1 ≤ p < ∞ and -2 < q < ∞. If$h=\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,q),$then |S _f (z)|^p(1 - |z|²)^p+qd A(z) is a K-Carleson measure.

Proof

Since f is univalent,

$$\begin{array}{l}\parallel \text{log}{f}^{\prime }{\parallel }_{\mathcal{B}}=\underset{aϵ\mathbb{D}}{\text{sup}}(1-|z{|}^2)|P_f(z)|\le 6.\end{array}$$

Thus by Theorem 4 with n = 1 and h =logf^′, we have $h=\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,q)$ if and only if

$$|P_f(z){|}^p{(1-|z{|}^2)}^q\mathit{\text{dA}}(z)\text{is a}\mathit{\text{K-Carleson measure.}}$$

(7)

Using Theorem 4 with n = 2, this is further equivalent to

$$|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{p+q}\mathit{\text{dA}}(z)\text{being a}\mathit{\text{K-Carleson measure.}}$$

(8)

For p ≥ 1, we get

$$\begin{array}{l}|S_f(z){|}^p\le 2^{p-1}|P_f^{\prime }(z){|}^p+\frac{1}{2}|P_f(z){|}^{2p}.\end{array}$$

Thus,

$$\begin{array}{ll}|S_f(z){|}^p{(1-|z{|}^2)}^{p+q}& \le 2^{p-1}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{p+q}\\ +\frac{1}{2}\parallel \text{log}{f}^{\prime }{\parallel }_{\mathcal{B}}|P_f(z){|}^p{(1-|z{|}^2)}^q.\end{array}$$

By (7) and (8) we have |S _f (z)|^p(1 - |z|²)^p+qd A(z) as a K-Carleson measure. The proof is completed.□

Schwarzian derivative and K-Carleson measure

In this section, we give Schwarzian derivative characterizations of the spaces $S_X=\{\text{log}{f}^{\prime }:fϵ\mathcal{U},\text{log}{f}^{\prime }ϵX\}$, where X is either a ${\mathcal{Q}}_K(p,q)$ or ${\mathcal{Q}}_{K,0}(p,q)$ space, contained in the Bloch space. Note that since ${\mathcal{Q}}_K(p,q)\subset {\mathcal{B}}_0$ whenever q + 2 < p,or q + 2= p and K (0) > 0, and ${\mathcal{Q}}_{K,0}(p,q)\subset {\mathcal{B}}_0$ whenever q + 2 ≤ p, we have S _X  ∩ T (1) = S _X , where X is one of these spaces and $T(1)=\{\text{log}{f}^{\prime }:f\text{has a quasiconformal extension to}\mathbb{D}\}.$ Thus, the main interests are the leftover options, i.e., the cases when $X={\mathcal{Q}}_K(p,p-2)$, K:[0,∞) → [0,∞), and 1 ≤ p < ∞, which are all Möbius-invariant ${\mathcal{Q}}_K(p,p-2)$ space.

Theorem 3

Let K:[0,∞) → [0,∞) satisfy (2), (3), 1 ≤ p < ∞ and -2 < q < ∞, further satisfying either q + 2 < p, or q + 2 = p and K (t) = 1.Then the following conditions are equivalent:$(i)\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,q).$$(\mathit{\text{ii}})\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0$and |S _f (z)|^p(1 - |z|²)^p+qd A(z) is a K-Carleson measure.

Proof

Recall that for the general choice of p,q and K satisfying (2) and (3), $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,q)\subset {\mathcal{B}}^{\frac{q+2}{p}}.$ Thus, if $q+2<p,{\mathcal{Q}}_K(p,q)\subset {\mathcal{B}}^{\alpha }$, with 0 < α < 1,which is a subspace of ${\mathcal{B}}_0.$ Thus, the proof of (i) ⇔ (ii) follows from Lemma 4 and Proposition 1. □

The case q + 2 = p and K (t) = 1, i.e., the case of the Besov spaces B _p , 1 < p < ∞,follows similarly, noting that each of these spaces is also included in ${\mathcal{B}}_0.$ This result also appears in [21].

Theorem 4

Let K:[0,∞) → [0,∞) satisfy (2), (3), 1 ≤ p < ∞ and -2 < q < ∞, further satisfying q + 2 = p. Then$\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,q)$if and only if |S _f (z)|^p(1 - |z|²)^p+qd A(z) is a K-Carleson measure.

Proof

The direction of the proof is already covered by Proposition 1. Since q = p - 2,we have ${\mathcal{Q}}_K(p,q)={\mathcal{Q}}_K(p,p-2)$, and we are left to prove that if

$$|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}\mathit{\text{dA}}(z)$$

is a K-Carleson measure, then $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,p-2).$ Both of these conditions are Möbius-invariant, and so,all that we really need to prove is that

$$\begin{array}{l}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty \end{array}$$

implies

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f(z){|}^p{(1-|z{|}^2)}^{p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty ,\end{array}$$

which is further equivalent to

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty .\end{array}$$

Since $|P_f^{\prime }(z){|}^p\le 2^{p-1}|S_f(z){|}^p+\frac{1}{2}|P_f(z){|}^{2p}$, we have

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le 2^{p-1}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +\frac{1}{2}{\int }_{\mathbb{D}}|P_f(z){|}^{2p}{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

As before, we may assume that P _f  is continuous on $\overline{\mathbb{D}}$ (the closed unit disk), for if not, we can first use r-dilatation P _f  and then take r → 1 at the end of the proof.We estimate the integral

$$\begin{array}{l}{I}_{P_f^2}(\mathbb{D})={\int }_{\mathbb{D}}|P_f(z){|}^{2p}{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\end{array}$$

by estimating parts of this integral over three subsets of $\mathbb{D.}$ For ε,δ > 0, let

$$\begin{array}{l}U=\{zϵ\mathbb{D}:|P_f(z)|(1-|z{|}^2)<\epsilon \},\end{array}$$

$$\begin{array}{l}V=\{zϵ\mathbb{D}:|S_f(z)|{(1-|z{|}^2)}^2>\delta \},\end{array}$$

and

$$\begin{array}{ll}\Delta & =\mathbb{D}\setminus (U\cup V)\\ =\{zϵ\mathbb{D}:|P_f(z)|(1-|z{|}^2)\ge \epsilon ,|S_f(z)|{(1-|z{|}^2)}^2\le \delta \}.\end{array}$$

By Theorem 1, there is E > 0 such that

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f(z){|}^p{(1-|z{|}^2)}^{p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le E{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z),\end{array}$$

so

$$\begin{array}{ll}{I}_{P_f^2}(U)& ={\int }_U|P_f(z){|}^{2p}{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ <{\epsilon }^p{\int }_U|P_f(z){|}^p{(1-|z{|}^2)}^{p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le {\epsilon }^p{\int }_{\mathbb{D}}|P_f(z){|}^p{(1-|z{|}^2)}^{p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le E{\epsilon }^p{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

Using |P _f (z)|(1 - |z|²) < 6,we have

$$\begin{array}{ll}{I}_{P_f^2}(V)& ={\int }_V|P_f(z){|}^{2p}{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ <6^{2p}{\int }_V{(1-|z{|}^2)}^{-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ <\frac{6^{2p}}{{\delta }^p}{\int }_V|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le \frac{6^{2p}}{{\delta }^p}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

For the estimate of

$$\begin{array}{l}{I}_{P_f^2}(\Delta )={\int }_{\Delta }|P_f(z){|}^{2p}{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z),\end{array}$$

we use a sequence {Q _j } of Carleson boxes, so

$$\begin{array}{ll}{I}_{P_f^2}(\Delta )& ={\int }_{\Delta }|P_f(z){|}^{2p}{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ <6^{2p}{\int }_{\Delta }K(1-|{\phi }_a(z){|}^2)\frac{\mathit{\text{dA}}(z)}{{(1-|z{|}^2)}^2}\\ \le 6^{2p}\sum _k\underset{T(Q_k)}{\int }K(1-|{\phi }_a(z){|}^2)\frac{\mathit{\text{dA}}(z)}{{(1-|z{|}^2)}^2}\\ \le 6^{2p}C\sum _j\ell [K(Q_j)].\end{array}$$

Combining the above and choosing ε such that E ε^p < 1, we get

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le & 2^{p-1}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +\frac{E{\epsilon }^p}{2}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +\frac{6^{2p}}{2{\delta }^p}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +6^{2p}C\sum _j\ell [K(Q_j)].\end{array}$$

By Lemma 3, we further have

$$\begin{array}{ll}\sum _j& \ell [K(Q_j)]\\ \le C_1+C_2{\int }_{\mathbb{D}}|\mathrm{S\phi }(z){|}^p{(1-|z{|}^2)}^{p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

Choosing C to represent a generic positive constant, we get

$$\begin{array}{l}\left(1-\frac{E{\epsilon }^p}{2}\right){\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le C{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

Thus,

$$\begin{array}{l}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty ,\end{array}$$

which implies that

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{2p-2}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty \end{array}$$

this is equivalent to $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_K(p,q)$, and this finishes the proof. □

Next, we give the results of the membership of logf^′ in the space

$${\mathcal{Q}}_{K,0}(p,q).$$

Theorem 5

Let K:[0,∞) → [0,∞) satisfy (2), (3), 1 ≤ p < ∞ and -2 < q < ∞, further satisfying q + 2 ≤ p. Then$\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q)$if and only if |S _f (z)|^p(1 - |z|²)^q+pd A(z) is a compact K-Carleson measure.

Proof

Since q + 2 ≤ p, we have ${\mathcal{Q}}_{K,0}(p,q)\subseteq {\mathcal{B}}_0.$ Thus, if $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q)$, to prove that |S _f (z)|^p(1 - |z|²)^q+pd A(z) is a compact K-Carleson measure, we start with the inequality

$$\begin{array}{l}|S_f(z){|}^p\le 2^{p-1}|P_f^{\prime }(z){|}^p+\frac{1}{2}|P_f(z){|}^{2p}.\end{array}$$

Thus,

$$\begin{array}{l}{\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{q+p}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ \le 2^{p-1}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{q+p}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)\\ +\frac{1}{2}\parallel \text{log}{f}^{\prime }{\parallel }_{\mathcal{B}}^p{\int }_{\mathbb{D}}|P_f(z){|}^p{(1-|z{|}^2)}^{q}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z).\end{array}$$

Taking limits as |a| → 1 on both sides of the inequality, by Theorem 2, we get that |S _f (z)|^p(1 - |z|²)^q+pd A(z) is a compact K-Carleson measure.

For the converse, let us assume that |S _f (z)|^p(1 - |z|²)^q+pd A(z) is a compact K-Carleson measure. We will first show then that $\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0$, i.e., |S _f (z)|(1 - |z|²)² → 0as |a|→1. Since q + 2 ≤ p, we have (1 - |z|²)^2p-2 ≤ (1 - |z|²)^q+p, and so |S _f (z)|^p(1 - |z|²)^2p-2d A(z) is also a compact K-Carleson measure. For $aϵ\mathbb{D}$, let

$$\begin{array}{l}E(a,1/e)=\{zϵ\mathbb{D}:|z-a|<\frac{1}{e}(1-|a|)\}.\end{array}$$

It is easy to see that

$$\begin{array}{l}\left(1-\frac{1}{e}\right)(1-|a|)\le (1-|z|)\le \left(1+\frac{1}{e}\right)(1-|a|)\end{array}$$

whenever z ϵ E(a,1/e).Using |S _f (z)|^p as a subharmonic function and the pseudo-hyperbolic disk $\mathbb{D}(a,1/e)$ and $E(a,1/e)\subset \mathbb{D}(a,1/e)$, we have

$$\begin{array}{l}|S_f(a){|}^p{(1-|a{|}^2)}^{2p}\\ \le K(1){\int }_{E(a,1/e)}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}\mathit{\text{dA}}(z)\\ \le K(1){\int }_{\mathbb{D}(a,1/e)}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}\mathit{\text{dA}}(z)\\ \le {\int }_{\mathbb{D}}|S_f(z){|}^p{(1-|z{|}^2)}^{2p-2}\le K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)<\infty .\end{array}$$

Therefore, |S _f (a)|^p(1 - |a|²)^2p < ∞, and so $\underset{|a|\to 1}{\text{lim}}|S_f(a)|{(1-|a{|}^2)}^2=0$, which is equivalent to $\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0.$

The rest of the proof follows similarly to the proof of Lemma 4, with appropriate adjustments. Using $\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0$, replacing the supremum over $aϵ\mathbb{D}$ with limit as |a| → 1, and using that for |z| < r, we have ${(1-|{\phi }_a(z))}^2\le \frac{1-|a{|}^2}{1-r}\to 0$ as |a| → 1. We get accordingly that if |S _f (z)|^p(1 - |z|²)^q+pd A(z) is a compact K-Carleson measure, then

$$\begin{array}{l}\underset{|a|\to 1}{\text{lim}}{\int }_{\mathbb{D}}|P_f^{\prime }(z){|}^p{(1-|z{|}^2)}^{q+p}K(1-|{\phi }_a(z){|}^2)\mathit{\text{dA}}(z)=0.\end{array}$$

Hence, $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q)$, and this finishes the proof. □

Jordan curve and ${\mathcal{Q}}_{\mathit{K}}(p,p-2)$ space

There are many interesting questions related to the topological structure of these types of general Teichmüller spaces and the geometry of the domains Ω. For example:

• Is it always true that $S_{{\mathcal{Q}}_K(p,p-2)}\cap T(1)$ is the interior of $S_{{\mathcal{Q}}_K(p,p-2)}$ in ${\mathcal{Q}}_K(p,p-2)$, and what is their closure in the ${\mathcal{Q}}_K(p,p-2)$ norm or in the Bloch norm?

• Are there specific descriptions of some of the connected components of $S_{{\mathcal{Q}}_K(p,p-2)}\cap T(1)$ via the dilatations of the quasiconformal extensions of the corresponding map f or in terms of specific conditions imposed on f?

• What are the specific geometric properties that either Ω or ∂ Ω has when logf^′ belongs to $S_{{\mathcal{Q}}_K(p,p-2)}$ or to $S_{{\mathcal{Q}}_K(p,p-2)}\cap T(1)$?

Recall that since f is univalent and ∂ Ω is a Jordan curve, ∂ Ω is rectifiable if and only if f^′ ϵ H¹ (see [19], Theorem 6.8). Furthermore, the Hardy-Stein-Spencer identity states that f^′ ϵ H^r,r > 0 if and only if

$$\begin{array}{l}{\int }_{\mathbb{D}}|f^{\mathrm{\prime \prime }}(z){|}^2|f^{\prime }(z){|}^{r-2}(1-|z{|}^2)\mathit{\text{dA}}(z)<\infty ,\text{(see [21])}.\end{array}$$

Note that since Ω is a bounded domain, we get that f belongs to the Dirichlet space $\mathcal{D},$ which is contained in the little Bloch space ${\mathcal{B}}_0.$ It is even more true whenever $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q).$ Namely, since all of the ${\mathcal{Q}}_{K,0}(p,q)$ spaces are contained in ${\mathcal{B}}_0$, then $\text{log}{f}^{\prime }ϵ{\mathcal{B}}^{\alpha },\alpha >0$ (see [14], p. 56).

By using equivalent, higher derivative versions of a weighted Bergman space norm, it is not to hard to see that if $\text{log}{f}^{\prime }ϵ{\mathcal{B}}_0$, i.e., $\underset{|z|\to 1}{\text{lim}}(1-|z{|}^2)\frac{|f^{\mathrm{\prime \prime }}(z)|}{|f^{\prime }(z)|}=0$, then

$$\begin{array}{l}{\int }_{\mathbb{D}}|f^{\prime }(z){|}^r{(1-|z{|}^2)}^t\mathit{\text{dA}}(z)<\infty ,\\ \text{for every}r>0\text{and every}t>-1\text{(see [14])}.\end{array}$$

For any α > 0, let r > 0 such that α r > 1, and let t = α r-2 > -1, then the finiteness of the integral above, with the chosen r and t, implies that $\underset{|z|\to 1}{\text{lim}}{(1-|z{|}^2)}^{\alpha }|f^{\prime }(z)|=0$, and so $fϵ{\mathcal{B}}^{\alpha }$. We have the following result related to the boundary Jordan curve ∂ Ω, which includes the cases mentioned above.

Theorem 6

Let K:[0,∞) → [0,∞) satisfy (1) and (2) with Kⁿ(g(z,a)) ≈ K(g(z,a));n > 0.Suppose that 1 ≤ p < ∞ and -2< q < ∞. If$\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q),$then f^′ ϵ  H^r for all r > 0, which furthermore implies that the Jordan curve ∂ Ω is rectifiable.

Proof

We will use a result from Theorem 3.2 of [22], stating that for a positive measure μ on $\mathbb{D}$ and any r,α > 0,

$$\begin{array}{l}{\int }_{\mathbb{D}}\frac{d\mu (z)}{{(1-|z{|}^2)}^{\mathrm{\alpha r}}}<\infty \end{array}$$

if and only if there is a positive constant C such that

$${\int }_{\mathbb{D}}|g^{\prime }(z){|}^{r}d\mu (z)\le C{\left(\parallel g{\parallel }_{{\mathcal{B}}^{\alpha }}+|g(0)|\right)}^r$$

(9)

for all analytic functions g in $\mathbb{D}$, in particular, for all $gϵ{\mathcal{B}}^{\alpha }$.

Let $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q).$ Since the space gets larger when the index p increases, we will first of all assume, without loss of generality, that p > 2. Secondly, since q ≤ p - 2 and ${\mathcal{Q}}_{K,0}(p,q)\subseteq {\mathcal{Q}}_{K,0}(p,p-2)$, we will consider only the case when q = p - 2. Thus, we want to prove that if $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,q),p>2$, then f^′ ϵ H^r for all r > 0, which by the Hardy-Stein-Spencer identity is equivalent to showing that

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f(z){|}^2|f^{\prime }(z){|}^r(1-|z{|}^2)K\left(g(z,a)\right)\mathit{\text{dA}}(z)<\infty .\end{array}$$

Since p > 2, let p^′ > 1 such that $\frac{2}{p}+\frac{1}{p^{\prime }}=1.$ Using Hölder’s inequality, for t ϵ (0,1), we get

$$\begin{array}{l}{\int }_{\mathbb{D}}|P_f(z){|}^2|f^{\prime }(z){|}^r(1-|z{|}^2)K\left(g(z,a)\right)\mathit{\text{dA}}(z)\\ \le {\left({\int }_{\mathbb{D}}|P_f(z){|}^p|f^{\prime }(z){|}^{\frac{\mathit{\text{rp}}}{2}}{(1-|z{|}^2)}^{p-2+t}K\left(g(z,a)\right)\mathit{\text{dA}}(z)\right)}^{\frac{2}{p}}\\ \times {\left({\int }_{\mathbb{D}}{(1-|z{|}^2)}^{\frac{4-p-2t}{p-2}}K\left(g(z,a)\right)\mathit{\text{dA}}(z)\right)}^{\frac{1}{p^{\prime }}}\\ \le C{\left(\parallel f{\parallel }_{{\mathcal{B}}^{\frac{2t}{\mathit{\text{rp}}}}}+|g(0)|\right)}^{\frac{\mathit{\text{rp}}}{2}}<\infty .\end{array}$$

The second inequality above holds since $\text{log}{f}^{\prime }ϵ{\mathcal{Q}}_{K,0}(p,p-2)$, and thus we can apply (9) to the measure

$$\begin{array}{l}d\mu (z)=|P_f(z){|}^p{(1-|z{|}^2)}^{p-2+t}K\left(g(z,a)\right)\mathit{\text{dA}}(z)\end{array}$$

to get $fϵ{\mathcal{B}}^{\frac{2t}{\mathit{\text{rp}}}}.$ Moreover, for K satisfying (1),

$$\begin{array}{l}{\int }_{\mathbb{D}}{(1-|z{|}^2)}^{\frac{4-p-2t}{p-2}}K\left(g(z,a)\right)\mathit{\text{dA}}(z)\\ ={\int }_{\mathbb{D}}{(1-|z{|}^2)}^{q}K\left(g(z,0)\right)\mathit{\text{dA}}(z)\\ =2\pi \underset{0}{\overset{1}{\int }}{(1-|r{|}^2)}^{q}K\left(\text{log}\frac{1}{r}\right)\mathit{\text{rdr}}<\infty \end{array}$$

since $q=\frac{4-p-2t}{p-2}\ge -1.$ The proof is completed. □

Remark 1

Note that the proof of Theorem 6 can be used for several cases, and we leave the details to the reader. The case when K (t) = t^s,0 ≤ s < 1,1 ≤ p < ∞,- 2 < q < ∞ and q + s > -1is the F₀(p,q,s) case which is covered in Zorboska’s result in [14]. Also, the case when K(t) = t,q = 0and p = 2 is the VMOA case (the space of functions analytic on $\mathbb{D}$ and with vanishing mean oscillation on the unit circle) which is covered in Pommerenke’s result in [23].