Bayesian change point estimation in Poisson-based control charts

Abstract

Precise identification of the time when a process has changed enables process engineers to search for a potential special cause more effectively. In this paper, we develop change point estimation methods for a Poisson process in a Bayesian framework. We apply Bayesian hierarchical models to formulate the change point where there exists a step change, a linear trend and a known multiple number of changes in the Poisson rate. The Markov chain Monte Carlo is used to obtain posterior distributions of the change point parameters and corresponding probabilistic intervals and inferences. The performance of the Bayesian estimator is investigated through simulations and the result shows that precise estimates can be obtained when they are used in conjunction with the well-known c-, Poisson exponentially weighted moving average (EWMA) and Poisson cumulative sum (CUSUM) control charts for different change type scenarios. We also apply the Deviance Information Criterion as a model selection criterion in the Bayesian context, to find the best change point model for a given dataset where there is no prior knowledge about the change type in the process. In comparison with built-in estimators of EWMA and CUSUM charts and ML based estimators, the Bayesian estimator performs reasonably well and remains a strong alternative. These superiorities are enhanced when probability quantification, flexibility and generalizability of the Bayesian change point detection model are also considered.

Background

Statistical process control charts are used to detect changes in a process by distinguishing between assignable causes and common causes of the process variation. When a control chart signals, process engineers initiate a search to identify and eliminate the source of variation. Knowing the time at which the process began to vary, the so-called change point, would help to conduct the search more efficiently in a tighter time-frame.

A Poisson process is often used to model the number of occurrences in an interval of time. In this regard, Poisson-based control charts have been developedand frequently applied in an industry context to monitor the number of defects and nonconformities in a product (Gardiner and Montgomery 1987; White et al. 1997) and in a health context to monitor patient mortality and spread of an infection in a hospital (Benneyan 1998; Limayea et al. 2008). The most commonly used control chart procedures adopted for Poisson-distributed data include c-charts (Shewhart 19261927), cumulative sum of quality characteristic measurement (CUSUM; Page 19541961; Brook and Evans 1972), and exponentially weighted moving average (EWMA; Roberts 1959; Trevanich and Bourke 1993; Borror and Rigdon 1998); see Woodall (1997) and Montgomery (2008) for more details. Furthermore, appropriate control charts and methods were developed in monitoring more complex Poisson data including correlated (Chiu and Kuo 2007; Niaki and Abbasi 2008; Niaki and Nafar 2008; Amiri et al. 2011) and auto-correlated observations (Weiß, 2007; Vermaat et al. 2008).

It has been shown that Poisson CUSUM and Poisson EWMA charts are more sensitive for detecting small shifts in the process parameters whereas a c-chart still remains efficient for the detection of large shifts (Montgomery 2008). However, upon signaling, none of them provide specific information regarding the time at which the process changed and the magnitude and the type of the change.

In recent years, statistical and machine-learning methods have been employed in the development of change point estimators for a broad range of processes and change types (Amiri and Allahyari 2012; Atashgar 2013). For Poisson processes, maximum likelihood (ML) methods were applied to estimate the true time of a step change (Samuel and Pignatiello 1998; Perry 2004) and a linear trend (Perry et al. 2006) in the Poisson rate. It was shown that more precise estimates were obtained when ML estimators were used in conjunction with Poisson control charts, compared to charts’ signals and CUSUM (Page 1954) or EWMA built-in estimators (Nishina 1992). A confidence interval on the estimated change point was also constructed (Perry 2004; Perry et al. 2006). Furthermore, Perry et al. (2007a) challenged the underlying assumption of knowing the form of change types and derived a ML estimator for non-decreasing multiple step change points (unknown number of consecutive changes) using isotonic regression models. The estimator was reported a reasonable alternative for some magnitudes of the step and linear trend disturbances. In the presence of multiple change points, it was found to be the superior. ML estimators have also been extended for step change scenarios in correlated Poisson observations (Niaki and Khedmati 2012; 2013a; Sharafi et al. 2013). Similar methods were extended to other attributes including binary data (Perry et al. 2007b; Noorossana et al. 2009; Amiri et al. 2011; Hou et al. 2013; Niaki and Khedmati 2013b).

A Bayesian formulation has recently been proposed as an alternative in change point estimation within a clinical context (Assareh et al. 2011a). It can easily capture complexity of patient mix and provide highly informative and precise estimates for the true time of a step change (Assareh et al. 2011c) or linear trend (Assareh et al. 2011b) in the odds ratio of clinical outcomes or mean survival time following a clinical procedure (Assareh and Mengersen 2012). Application of the Bayesian framework to change point estimation provides a way of making a set of inferences based on posterior distributions for the time and the magnitude of a change as well as assessing the validity of underlying assumptions in the change point model itself (Gelman et al. 2004).

In this paper, we model the change point in a Poisson process using a Bayesian framework and compare the performance of the Bayesian estimator with ML estimators. We model and estimate change points assuming that the underlying change type is known. In this scenario, the changes are in the form of a step change, a linear trend and a multiple change with known number of changes. For each model, we analyze and discuss the performance of the Bayesian change point model through posterior estimates and probability-based intervals. The three models are demonstrated and evaluated in sections ‘Bayesian change point model’, ‘Evaluation’, and ‘Performance analysis’ and then compared with respect to goodness of fit in section ‘Comparative performance and model selection’. We then compare the Bayesian estimator with ML estimators and others in section ‘Comparison of Bayesian estimator with other methods’ and summarize the study and obtained results in section ‘Conclusion’.

Bayesian change point model

Statistical inferences for a quantity of interest in a Bayesian framework are described as the modification of the uncertainty about their value in the light of evidence, and Bayes’ theorem precisely specifies how this modification should be made as below:

$$\text{Posterior}\propto \text{Likelihood}\times \text{Prior},$$

(1)

where ‘Prior’ is the state of knowledge about the quantity of interest in terms of a probability distribution before the data are observed; ‘Likelihood’ is a model underlying the data, and ‘Posterior’ is the state of knowledge about the quantity after data are observed which also is in the form of a probability distribution. This structure is expendable to multiple levels in a hierarchical fashion, so-called Bayesian hierarchical models (BHM), which allows to enrich the model by capturing all kinds of uncertainties for data observed as well as priors. In complicated BHMs, it is not easy to obtain the posterior distribution analytically. This analytic bottleneck has been eliminated by the emergence of Markov chain Monte Carlo (MCMC) methods. In MCMC algorithms, a Markov chain, also known as a random walk, is constructed whose stationary distribution is the posterior distribution of the parameters. Samples generated from a long run of the Markov chain using a proposal transition density are drawn from posterior distributions of interest. Some common MCMC methods for drawing samples include Metropolis-Hastings and the Gibbs sampler (see Gelman et al. (2004) for more details).

Consider a Poisson process X _t , t=1,…,T, that is initially in-control, with independent observations coming from a Poisson distribution with a known rate λ₀. At an unknown point in time, τ, the Poisson rate parameter changes from its in-control state of λ₀ to λ₁, λ₁=λ₀+δ,δ≠0. The Poisson process step change model can thus be parameterized as follows:

$$\begin{array}{c}p(x_t\mid {\lambda }_t)=\left\{\begin{array}{cc}\text{exp}(-{\lambda }_0){\lambda }_0^{x_t}/x_t!& \mathit{\text{if}}t=1,2,\dots ,\tau \\ \text{exp}(-{\lambda }_1){\lambda }_1^{x_t}/x_t!& \mathit{\text{if}}t=\tau +1,\dots ,T,\end{array}\right.,\end{array}$$

(2)

where δ is the magnitude of the step change and τ and T are the change time and the current time, respectively.

The departure from the in-control state may occur due to a non-constant change type scenario which can be explained by a linear trend model λ _t =λ₀+β(t−τ) for t>τ. In this model, β is the magnitude of the linear trend disturbance (slope) in the process parameter and its positive value implies an increasing trend in which λ _t >λ₀, while a negative β leads to a linear reduction of the Poisson rate and λ _t <λ₀ for t=τ+1,…,T. The Poisson process linear trend change model can be modelled as follows:

$$\begin{array}{c}p(x_t\mid {\lambda }_t)=\left\{\begin{array}{cc}\text{exp}(-{\lambda }_0){\lambda }_0^{x_t}/x_t!& \mathit{\text{if}}t=1,2,\dots ,\tau \\ \text{exp}(-({\lambda }_0+\beta (t-\tau )\left)\right)\\ {({\lambda }_0+\beta (t-\tau \left)\right)}^{x_t}/x_t!& \mathit{\text{if}}t=\tau +1,\dots ,\mathrm{T.}\end{array}\right.\end{array}$$

(3)

In order to address the possibility of having change types other than step and linear trend forms (Perry et al. 2007a), we introduce a multiple change point scenario where the number of change points is known. This prior knowledge might have been obtained based on awareness and past experience of process engineers in factors such as changes in operators, materials, procedures, tools, and policies which may lead to increasing or decreasing step changes in the Poisson rate. Here, we consider the case of two sequential step changes. Other cases with more than two change points can be modelled in the same way. In this scenario, at an unknown point in time, τ₁, the Poisson rate parameter changes from its in-control state of λ₀ to λ₁, λ₁=λ₀+δ₁,δ₁≠0. For a period of time, the process continues with the new parameter, λ₁, and then at an unknown point in time, τ₂, it changes to λ₂, λ₂=λ₀+δ₂,δ₂≠δ₁≠0. The Poisson process multiple change point model with two step changes can thus be parameterized as follows:

$$p(x_t\mid {\lambda }_t)=\left\{\begin{array}{cc}\text{exp}(-{\lambda }_0){\lambda }_0^{x_t}/x_t!& \mathit{\text{if}}t=1,2,\dots ,{\tau }_1\\ \text{exp}(-{\lambda }_1){\lambda }_1^{x_t}/x_t!& \mathit{\text{if}}t={\tau }_1+1,\dots ,{\tau }_2\\ \text{exp}(-{\lambda }_2){\lambda }_2^{x_t}/x_t!& \mathit{\text{if}}t={\tau }_2+1,\dots ,\mathrm{T.}\end{array}\right.$$

(4)

Regarding above models to Equation 1, p(.∣.), is the likelihood that underlies the observations; and posterior distributions of the time (τ, τ₁, τ₂) and the magnitude of change (δ, β, δ₁, δ₂) will be constructed and investigated as they are the unknown parameters of interest in the change point analysis. Assume that the process X _t is monitored by a control chart that signals at time T. We assign a zero-mean normal distribution with a standard deviation of $6\times \sqrt{{\lambda }_0}$ as a prior distribution for all change sizes (δ, β, δ₁, δ₂). This is a reasonably informative prior for the magnitude of the change in an in-control Poisson rate as the control chart is sensitive enough to detect very large shifts and estimate associated change points. Other distributions such as uniform or Gamma might also be of interest; see Gelman et al. (2004) for more details on selection of prior distributions. We place a uniform distribution on the range of (1, T−1) as a prior for the time of the change (τ, τ₁, τ₂). To avoid obtaining a negative value for process mean after a change, λ₁₍₂₎, within MCMC, particularly when a drop has occurred, we added a constraint such that λ₁₍₂₎ must be positive. Although other methods such as modelling the process on the log scale may be of interest, we do not pursue these here as we may lose simplicity and explicit or correct reflection of the Poisson process. See the Appendix for the change model codes in WinBUGS (Spielgelhalter et al. 2003).

Evaluation

We used Monte Carlo simulation to study the performance of the constructed BHMs in change estimation following a signal from c-, Poisson CUSUM, and Poisson EWMA control charts when a change (step, linear, multiple) is simulated to occur at τ=100. We generated 100 observations of a Poisson process with an in-control rate of λ₀=20. To investigate the behavior of the Bayesian estimators over the population for different change sizes, we replicated this simulation method 100 times. Simulated datasets that were obvious outliers were excluded. This setting allows us to have distribution of estimates with standard errors in orders of 10. The number of replication studies is a compromise between excessive computational time, considering MCMC iterations and sufficiency of the achievable distributions even for tails.

In the step of change scenario, we induced step changes of sizes δ={+2,+6} as an example and δ={±2,±6,±15} for a replication study until the control charts signalled. In the linear trend model, changes of slopes β={±0.5,±1.0,±2.0} were induced until the control charts signalled. For the multiple change point case, two consecutive changes are simulated to occur at (τ₁,τ₂)=(100,110). We induced two changes of sizes (δ₁,δ₂)={(±4,±8),(±4,±12)} as part of a replication study at the determined times of change (τ₁,τ₂) until the control charts signalled. In this scenario, the replication study was limited to c-chart, since other control charts mostly signalled prior to the induction of the second change point.

Because we know that the process is in-control, if an out-of-control observation was generated in the simulation of the early 100 in-control observations, it was taken as a false alarm and the simulation was restarted. However, in practice, a false alarm may lead to stopping the process and analyzing root causes. When no cause is found, the process would follow without adjustment. Furthermore, for the multiple change scenario, if in any simulation, the charts signalled earlier than simulating the second change, that simulation was terminated and not followed. The simulation was also repeated for rate parameters of 5 and 10 over equivalent change scenarios; since the results were similar to these obtained for λ₀=20, they are not reported here.

To construct control charts, we applied the Shewhart (19261927), Brook and Evans (1972), and Trevanich and Bourke (1993) procedures for c-, Poisson CUSUM, and Poisson EWMA control charts, respectively. A Poisson CUSUM accumulates the difference between an observed value and a reference value k through $S_i^{+}=max\{0,x_i-k^{+}+S_{i-1}^{+}\}$ and $S_i^{-}=max\{0,k^{-}-x_i+S_{i-1}^{-}\}$, where $k^{+}=({\lambda }_1^{+}-{\lambda }_0)/\left(\text{ln}\right({\lambda }_1^{+})-\text{ln}({\lambda }_0\left)\right)$ and $k^{-}=({\lambda }_0-{\lambda }_1^{-})/\left(\text{ln}\right({\lambda }_0)-\text{ln}({\lambda }_1^{-}\left)\right)$. If $S_i^{\pm }$ exceeds a specified decision interval h^± then the control chart signals that an increase (a decrease) in the Poisson rate occurred. We calibrated the charts to detect a 25% shift in Poisson rates and have an in-control average run length (${\mathrm{A}\widehat{\mathrm{R}}\mathrm{L}}_0$) of 370 approximately, close to a standard c-chart (see Woodall and Adams (1993)). The resultant Poisson CUSUM charts had (k⁺,h⁺)=(22.4,22) and (k⁻,h⁻)=(17.4,14). For simplicity, the values were rounded to one decimal place.

In a Poisson EWMA cumulative values of observations are obtained through Z _i =r×x _i +(r−1)×Z_i−1, where Z₀=λ₀, and plotted in a chart with $\text{UCL}={\lambda }_0+A^{+}\sqrt{\text{Var}{Z}_i}$ and $\text{LCL}={\lambda }_0-A^{-}\sqrt{\text{Var}{Z}_i}$. We let r=0.1 and A^±=2.67 to build a chart with an ARL₀ of 370, close to a standard c-chart.

All changes and control charts were simulated in the R package. To obtain posterior distributions of the time and the magnitude of the changes, we used the R2WinBUGS interface (Sturtz et al. 2005) to generate 100,000 samples through MCMC iterations in WinBUGS (Spielgelhalter et al. 2003) for all change point scenarios with the first 20,000 samples ignored as burn in. We then analyzed the results using the CODA package in R (Plummer et al. 2010). See the Appendix for the change point model codes in WinBUGS.

Performance analysis

Step change model

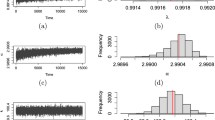
The posterior distributions for the time and the magnitude of a step change of size +6 are presented in Figure 1. For all control charts, posterior distributions of the change point concentrate on the 100th sample which is the real change point. Since the posteriors are asymmetric and skewed, particularly for the time of the change, the posterior mode is used as an estimator for change point model parameters (τ,δ).

Figure 1

Posterior distributions of the time τ and the magnitude δ of a step change ( λ ₀ =20, δ =+ 6, τ =100) following signals from (a, b) c-chart, (c, d) Poisson EWMA and (e, f) Poisson CUSUM.

Table 1 shows the posterior estimates for increases of sizes +2 and +6 in the process mean. The c-chart detects a fall of around half a standard deviation (δ=+2) in the Poisson rate after 101 samples where the mode of the posterior distribution reports the 101st sample as the change point. For a medium-shift size, δ=+6, around one-and-a-half standard deviation, the posterior mode concentrates on the 100th sample whereas the c-chart signals with 38 samples delay. The Poisson EWMA chart detects the shifts +2 and +6, after 42 and 13 samples, where the posterior distributions report the 103rd and 100th samples as the change points, respectively. This result implies that although the obtained posterior modes overestimate the change point for small shifts, they still perform relatively better than the Poisson EWMA chart. The resultant posteriors from a Poisson CUSUM are almost identical to those from Poisson EWMA. Bayesian estimates of the magnitude of the change tend to estimate small shifts almost precisely. However, the medium shift sizes are underestimated, although this slight bias must be considered in the context of their corresponding standard deviations.

Table 1 Posterior estimates (mode, SD) of step change point model parameters τ and δ following signals (RL)

Applying the Bayesian framework enables us to construct probability-based intervals around estimated parameters. A credible interval (CI) is a posterior probability-based interval which involves those values of highest probability in the posterior density of the parameter of interest. Table 2 presents 50% and 80% credible intervals for the estimated time and the magnitude of step changes in all three control charts. As expected, the CIs are affected by the dispersion and higher order behaviors of the posterior distributions. Under the same probability of 0.8 for the c-chart, the CI for the time of the step change of size δ=+2 covers 53 samples around the 100th sample whereas it decreases to 6 samples for δ=+6 due to the smaller standard deviation (see Table 1).

Table 2 Credible intervals for step change point model parameters τ and δ

The comparison of the 50% and 80% CIs for the estimated time of a step change of size δ=+6 in the Poisson EWMA chart reveals that the posterior distribution of the time is highly left skewed and the increase in the probability contracts the left boundary of the interval, from 96.9 to 88 in comparison with the shift in the right boundary. This investigation can be extended to other shift sizes and control chart scenarios for the time estimates. As shown in Table 1 and discussed above, the magnitude of the changes are not estimated as precisely as the time. However, Table 2 shows that in most cases for δ=+2, the real size of change are contained in the respective posterior 50% and 80% CIs.

Having a distribution for the time of the change enables us to make other probabilistic inferences. As an example, Table 3 shows the probability of the occurrence of the change point in the last 10, 25, and 50 observed samples prior to signalling in the control charts. For a step change of size δ=+2, since the c-chart signals very late (see Table 1), it is unlikely that the change point occurred in the last 10, 25, and even 50 samples. In contrast, in the Poisson EWMA and CUSUM charts, where they both signal earlier than the c-chart, the probabilities of occurrence in the last 10 samples are 0.55 and 0.59, then increase to 0.76 and 0.82, respectively as the next 15 samples are included. In the case of δ=+6, most of the probability density (0.98) is located between the last 25 and 50 samples for the c-chart, whereas with 0.80, it is between the last 10 and 25 samples for the Poisson EWMA chart and with probability 0.91, it is in the last 10 samples for the Poisson CUSUM chart. These kinds of probability computations and inferences can be extended to other change scenarios.

Table 3 Probability of occurrence of change point in last 10, 25, and 50 observed samples prior to signalling

Table 4 shows the average of the estimated parameters obtained from the 100 replicated datasets. As seen, although the c-chart detects small to medium shifts with a large delay, it performs better where there exists a jump. Having a longer delay in the detection of a decrease in the Poisson rate in comparison with an increase of the same size in the c-chart is due to the equality of mean and the variance of the Poisson distribution. Therefore, a fall in the mean leads to less dispersed observations. The Poisson EWMA and CUSUM charts behave in the same manner.

Table 4 Average of posterior estimates (mode, SD) of step change point model parameters τ and δ following signals (RL)

For a step change of size around half a standard deviation (δ=±2) in the Poisson rate, the average of the modes, $E\left(\widehat{\tau }\right)$, reports the 103^rd sample as the change point in all three control charts, whereas the charts detect the changes with delays greater than 17 samples, obtained in the Poisson CUSUM. This superiority persists where a medium shift of size δ=±6 has occurred in the process mean. As expected, for large-shift sizes (δ=±15), around three standard deviations, all control charts perform well, yet the mean of modes outperform them by a delay of less than one observation.

Table 4 reveals that in all three control charts, the variation of Bayesian estimates for time tends to reduce when the magnitude of shift in the process mean increases. However, by the nature of the Poisson distribution, for small to medium drops, δ=(−2,−6), the observed variation is less than those obtained in the estimation of jumps. The mean of the standard deviation of the posterior estimates of time, $E\left({\sigma }_{\widehat{\tau }}\right)$, also decreases by moving for small-shift sizes to medium and large sizes in the Poisson EWMA and CUSUM charts. In contrast, the greatest variation is obtained for a large shift of size δ=±15 in the c-chart. This is due to the early detection of such shifts by the c-chart that leads to a very short run of samples after the change which then compresses the data and hence informs the MCMC algorithm.

The average of the Bayesian estimates of the magnitude of the change, $E\left(\widehat{\delta }\right)$, shows that the modes of posteriors for change sizes do not perform as well as the posterior distributions of the time across different shift sizes; however, promising results are obtained where a small shift, δ=±2, has occurred in the process mean. This estimator tends to underestimate the sizes, particularly where there exists a jump. This bias increases when the shift size increases since a very short run of samples coming from the out-of-control state of the process with a high variance was used. As seen in Table 4, the best estimates are obtained in Poisson EWMA cases. Having said that, Bayesian estimates of the magnitude of the change must be studied in conjunction with their corresponding standard deviations. In this manner, analysis of credible intervals would be effective.

Linear trend model

Posterior distributions and probabilistic intervals and inferences are obtainable for the time and the slope of the linear trend, similar to the step change scenario illustrated in section ‘Step change model’. We, here, limited our results to the replication study over the simulated datasets outlined in section ‘Evaluation’.

Table 5 shows the average of the estimated parameters over trends with slope sizes of β={±0.50,±1.0,±2.0}. For a linear trend with small slopes of size β=±0.5 in the Poisson rate, the average modal value, $E\left(\widehat{\tau }\right)$, reports the 105th sample and less as the change point in all three control charts, whereas the charts detect the changes with delays greater than 10 samples, obtained in the Poisson CUSUM. This superiority also persists where a trend with larger slopes of size β=±1.0,±2.0 has occurred in the process mean. In these scenarios, the bias of the Bayesian estimator does not exceed two and one samples, where the minimum delays are seven and four samples, respectively.

Table 5 Average of posterior estimates (mode, SD) of linear trend change point model parameters τ and β following signals (RL)

Table 5 shows that in all three control charts, the variation of the Bayesian estimates for time tends to reduce when the magnitude of slope increases. The mean of posterior standard deviation for time, $E\left({\sigma }_{\widehat{\tau }}\right)$, also decreases by moving for small slope sizes to medium and large sizes in both directions. However, the observed variation for estimation of a decreasing trend is less than those obtained for an increasing trend with the same slope size.

The average of the posterior estimates for the magnitude of the change, $E\left(\widehat{\beta }\right)$, shows that the modes of the posteriors for change sizes perform as well as the posterior estimates of the time, particularly, for the c-chart and Poisson EWMA chart. In the CUSUM chart, the posteriors tend to underestimate the slope sizes.

Multiple change model

We applied the multiple change point model following signals of the c-chart as the Poisson EWMA and CUSUM mostly signalled before simulating the second change in the process. Although results here are limited to the replication study, distribution of parameters and probabilistic inferences can easily be constructed.

As seen in Table 6 and discussed in section ‘Step change model’, the c-chart signals earlier when a larger shift, either an increase or decrease, has occurred in the second change; however, it performs better where there exists a jump, regardless of the direction of the first change. The chart alarmed after 38 samples when two consecutive drops of sizes around one and two standard deviations, δ_1,2=(−4,−8), occurred. Although this delay falls to 16 samples when the second change has happened in the opposite direction, the modes of posteriors for the time of the first change, $E\left(\widehat{{\tau }_1}\right)$, outperform the chart. This superiority persists when the size of the second change increases to around three standard deviations, δ₂=(±12). The same results are also obtained, where the first change is an increase in the magnitude of one standard deviation, δ₁=(+4).

Table 6 Average of posterior estimates (mode, SD) of multiple step change point model parameters τ _1,2 and δ _1,2 following signals (RL)

Table 6 reveals that the Bayesian estimator tends to underestimate the time of the first change of two monotonic changes where the second change is of size δ₂=(±12). The associated variation, within replications, increases when the second step change increases in the same direction of the first change. The minimum variations of the posterior distributions for the time of the first change, $E\left({\widehat{\sigma }}_{\widehat{{\tau }_1}}\right)$, are obtained where there exist non-monotonic changes (see δ_1,2=(−4,+8) and δ_1,2=(+4,−8)). This variation also increases when the second step change increases in the same direction of the first change.

The time of the second step change is estimated precisely by the posterior modes. Table 6 shows that the average, $E\left(\widehat{{\tau }_1}\right)$, mostly concentrate on the 110th sample. Surprisingly, the variation between replications and also the variation of posterior distributions obtained for the time of the second change, $E\left({\widehat{\sigma }}_{\widehat{{\tau }_1}}\right)$, are less than those obtained for the first step change.

The average of the posterior estimates of the magnitude of the changes, $E\left(\widehat{{\delta }_1}\right)$ and $E\left(\widehat{{\delta }_2}\right)$, shows that the modes of the posteriors for change sizes do not perform as well as the posterior distributions of the time across different scenarios. The modes tend to underestimate the sizes, particularly, for jumps in either the first or the second step change. However, there still exists some gain in studying the estimated sizes and directions, particularly when the obtained standard deviations are also considered.

Comparative performance and model selection

We used Monte Carlo simulation to study the performance of the developed change point models in different change point scenarios following a signal from a c-chart. We generated 100 observations of a Poisson process with an in-control rate of λ₀=20. We then induced a step, a linear trend, and a multiple change in the Poisson rate. For each scenario the three change point models were applied and the time of the change was estimated. Based on the MCMC simulation, the Deviance Information Criterion (DIC) and related parameters, mean and variance of the posterior distribution of the deviance and the penalty value, were recorded. The DIC is a goodness of fit criterion which takes into account the deviance of the model, −2log(p(y∣θ)), and a penalty for the model complexity, p _D (Spielgelhalter et al. 2002). To allow for asymmetry in the posterior distribution, seen in Figure 1, p _V was used as an alternative to p _D , where p _V is half of the variance of the posterior distribution of the deviance (Gelman et al. 2004).

Table 7 indicates that the Bayesian estimate of a step change outperforms other Bayesian estimates, linear and multiple, where there is a step change in the process parameter. It estimates 101.9 and 108.3 as the times of change of sizes δ=−4 and δ=+4, respectively, whereas the linear model underestimates the time with a bias of around 55 and 24 samples and the multiple model tends to overestimate it relative to the step model. According to the reported DICs, the DIC _V supports that the step model with values of 1,167 and 845.5 is a preferable fit where there exists either an increasing or a decreasing step change.

Table 7 Performance and goodness of change point models on different change types following signal

In the case of an occurrence of a linear trend shift in the Poisson rate, the Bayesian estimate of a linear trend change outperforms other Bayesian estimates in estimating the change point. The reported DIC _V is convincing that the linear model with values of 603.7 and 630.9 is also the best fit. These results can be extended to the multiple change scenario. Table 7 shows that the Bayesian estimate of a multiple change (two changes) outperforms other Bayesian estimates, step and linear, where there are two consecutive changes in the Poisson rate. Similarly, the reported DIC _V supports that the multiple model with values of 636.4 and 791.2 is also the best fit in this case.

Comparison of Bayesian estimator with other methods

To study the performance of the proposed Bayesian estimators in comparison with those introduced in section ‘Background’, we run the alternatives, built-in estimators of Poisson EWMA and CUSUM charts and ML estimators, within replications as discussed in section ‘Evaluation’.

Table 8 shows the mean of Bayesian estimates and detected change points provided by built-in estimators of EWMA (Nishina 1992) and CUSUM (Page 1954) charts and the ML estimator (Perry 2004) for a step change in a Poisson process.

Table 8 Average of estimated time of a step change in a Poisson process obtained by Bayesian estimators, CUSUM and EWMA built-in estimators, and ML estimator following signals (RL)

Although the Bayesian estimator,${\widehat{\tau }}_b$, tends to overestimate the time of a step change of small sizes, δ=±2, with a delay of three samples, it outperforms the ML estimator,${\widehat{\tau }}_{\text{MLE}}$, which underestimates the time by six samples following a signal from the c-chart. For step sizes of one and half and three standard deviations, the ML estimator performs slightly better than the Bayesian estimator; however considering the obtained standard deviations decreases this superiority, particularly where there exists a jump in the process mean.

Table 8 reveals that the EWMA estimator,${\widehat{\tau }}_{\text{EWMA}}$, underestimates the change point when the size of shift increases for both directions where the Bayesian estimator tends to be more precise.${\widehat{\tau }}_b$ still remains the best estimator for small changes and shows acceptable performance in comparison with${\widehat{\tau }}_{\text{MLE}}$ over larger shifts, particularly when the standard deviations are taken into account.

The CUSUM estimator,${\widehat{\tau }}_{\text{CUSUM}}$, outperforms the equivalent estimators in EWMA for larger shifts, δ=(±6,±15); however, it overestimates the time of small shifts significantly. Similar to c-chart and EWMA cases, in CUSUM, the Bayesian estimator outperforms alternatives for small shifts and offers acceptable performance over other shift sizes, considering the obtained standard deviations over replications.

Table 9 shows the mean of the Bayesian estimates and detected change points provided by built-in estimators of EWMA (Nishina 1992) and CUSUM (Page 1954) charts and the ML estimator (Perry et al. 2006) for a linear trend change in a Poisson process. Application of the proposed ML estimator is restricted to trends with a positive slope as Newton’s method is not tractable for decreasing trends in Poisson mean; see Perry et al. (2006) for more details.

Table 9 Average of estimated time of linear trend in Poisson process obtained by Bayesian estimator, CUSUM and EWMA built-in estimators, and ML estimator following signals (RL)

The Bayesian estimator, ${\widehat{\tau }}_b$, almost outperforms the built-in estimator of EWMA, ${\widehat{\tau }}_{\text{EWMA}}$, where there exists a decreasing trend. This superiority increases when the slope size raises, β=−2. The CUSUM estimator, ${\widehat{\tau }}_{\text{CUSUM}}$, estimates the change point more precisely than the EWMA; however the Bayesian estimator, ${\widehat{\tau }}_b$, still remains the best alternative for detection of linear trends with negative slopes, when the variation of the estimates is taken into account.

Table 9 reveals that the Bayesian estimator, ${\widehat{\tau }}_b$, is slightly outperformed by the ML estimator, ${\widehat{\tau }}_{\mathrm{MLE}}$, across the charts when there exists an increasing linear trend in the process mean. Having said that, the Bayesian estimator can still be a reasonable alternative in light of the obtained standard deviations which are less than those observed from the ML estimator over replications.

The ML estimator proposed by Perry et al. (2007a) is suitable for monotonic consecutive changes. In contrast, the Bayesian estimator for a known number of change points proposed in section ‘Multiple change model’ can also be applied where there exists non-monotonic consecutive changes in the process mean. Therefore, the comparison study was not followed for the multiple change point case as there is no appropriate ML alternative against which to evaluate the Bayesian estimator. Similarly, the built-in EWMA and CUSUM estimators cannot be studied as they tend to signal before the second change point. In the case of signalling after the second change, they also failed as they tend to concentrate on the time of the latter step change as the change point in non-monotonic scenarios.

Apart from the accuracy and precision criteria used for the comparison study, the posterior distributions for the time and the magnitude of a change enable us to construct probabilistic intervals around estimates and probabilistic inferences about the location of change point as discussed in section ‘Step change model’ for the step change scenario. This is a significant advantage of the proposed Bayesian approach. Although similar results may be obtained when resampling in conjunction with ML methods, the inferential basics of this approach is more limited; see Bernardo and Smith (1994) for more details. Furthermore, flexibility of Bayesian hierarchical models, ease of extension to more complicated change scenarios such as combination of steps and linear and nonlinear trends, relief of analytic calculation of likelihood function, particularly for non-tractable likelihood functions and ease of coding with available packages should be considered as additional benefits of the proposed Bayesian change point model for monitoring purposes. This approach can be easily applied for other types of data and processes such as Bernoulli, normal and exponential family data and the mentioned advantages remain achievable.

The two-step approach to change point identification described in this paper has the advantage of building on control charts that may be already in place in practice. An alternative may be to retain the two-step approach but to use a Bayesian framework in both stages. There is now a substantial literature on Bayesian formulation of control charts and extensions such as monitoring processes with varying parameters (Feltz and Shiau 2001), over-dispersed data (Bayarri and Garcia-Donato 2005), start-up and short runs (Tsiamyrtzis and Hawkins 20052008). A further alternative is to consider a fully Bayesian, one-step approach, in which both the monitoring of the in-control process and the retrospective or prospective identification of changes is undertaken in the one analysis. This is the subject of further research.

Conclusion

Identification of the time when a process has changed enables process engineers to pursue investigation of special causes more effectively. Indeed, knowing the change point restricts the search efforts to a tighter window of observations and related variables. In this paper, we modeled the change point estimation for a Poisson process in a Bayesian framework. We considered three scenarios of changes, a step change, a linear trend, and a multiple change when the number of changes is known. We constructed Bayesian hierarchical models and derived posterior distributions for change point estimates using MCMC. We compared the performance of the Bayesian estimators with c-, Poisson EWMA, and CUSUM control charts. The results showed that the Bayesian estimates outperform standard control charts in change estimation, particularly where there exists a small to medium size of step change(s) and a linear trend change with small to relatively large magnitude of slope. In comparison with built-in estimators of EWMA and CUSUM and ML-based estimators, the Bayesian estimator performs reasonably well and remains a strong alternative, particularly when other criteria such as probability quantification through credible intervals and probabilistic inferences, flexibility, generalization, and simplicity are taken into accounts.

The investigation on the performance of the Bayesian estimates over different change scenarios reveals that each Bayesian change point model outperforms other models where its underlying change type has occurred in the Poisson process. The results also support the idea of using DIC as a primary step in change point estimation which can direct process engineers to identify the appropriate change point model before making inferences about the derived underlying changes in the process.

Appendix

The following are the different change model codes:

• 1. Step change model

  model {

  for (i in 1:RL _c ){

  xc[i] ∼ dpois(lambda2[i])

  lambda1[i]=lambda0+delta × step(i-change)

  lambda2[i]=max(lambda1[i],0.000001) }

  tau=1/(6 × sqrt(lambda0))

  RL=RL _c −1

  delta ∼ dnorm(0, tau)

  change ∼ dunif(1,RL) }

• 2. Linear trend change model

  model {

  for (i in 1:RL _c ){

  xc[i] ∼ dpois(lambda2[i])

  lambda1[i]=lambda0+beta × (i-change) × step(i-change)

  lambda2[i]=max(lambda1[i],0.000001) }

  tau=1/(6 × sqrt(lambda0))

  RL=RL _c −1

  beta ∼ dnorm(0, tau)

  change ∼ dunif(1,RL) }

• 3. Multiple change model

  model {

  for (i in 1:RL _c ){

  xc[i] ∼ dpois(lambda2[i])

  lambda1[i]=lambda0+delta1 × step(i-change1) × step(change2-i)+delta2 × step(i-change2)

  lambda2[i]=max(lambda1[i],0.000001) }

  tau=1/(6 × sqrt(lambda0))

  RL=RL _c −1

  delta1 ∼ dnorm(0, tau)

  delta2 ∼ dnorm(0, tau)

  change1 ∼ dunif(1,change2)

  change2 ∼ dunif(change1,RL) }

Authors’ information

HA is a research fellow at the University of New South Wales. His primary research interests include Bayesian methods and engineering statistics and its applications in statistical quality control. RN is Professor of Industrial Engineering at Iran University of Science and Technology. His primary research interests include statistical process control, process optimization, Six Sigma, and statistical analysis. KM is Professor of Statistics at Queensland University of Technology. Her research interests are Bayesian statistics, mixture models, hierarchical modelling and meta-analysis.