1 Introduction

Data science, as an interdisciplinary field, plays a pivotal role in extracting knowledge and insights from complex and large-scale datasets. It encompasses a wide range of techniques, methodologies, and tools to analyse and interpret data, enabling evidence-based decision making and driving innovation across various domains [1,2,3,4].

Data science involves the integration of statistical analysis, machine learning, data mining, and visualization techniques to extract actionable insights from data. It encompasses the entire data lifecycle, including data collection, cleaning, integration, transformation, modeling, and interpretation. By applying rigorous statistical methods and computational algorithms, Data Scientists can uncover patterns, trends, and correlations within data, enabling organizations to make data-driven decisions and gain a competitive advantage [5, 6].

The rise of big data has presented both opportunities and challenges in the field of Data Science. On one hand, Big Data offers vast amounts of information that can uncover valuable insights and patterns. On the other hand, the sheer volume, velocity, and variety of data pose significant computational and analytical challenges, which means traditional statistical methods may not be scalable or efficient enough to handle such data [7,8,9,10].

The application of statistical methods in data science provides the foundation for understanding data patterns, making inferences, and predicting outcomes. By using statistical techniques, meaningful insights, robust models, and informed decisions based on data-driven evidence can be extracted [6, 11,12,13,14].

Within the scope of data science and statistics, change point detection serves as a pivotal tool for identifying shifts or transitions in data patterns. By effectively detecting change points, Data Scientists can gain profound insights into anomalies, events, or structural transformations embedded within the data [15].

The application of change point detection methods, including Bayesian approaches, holds significant importance in data science. Bayesian change point detection employs Bayesian inference principles to estimate the posterior probability of change points by incorporating prior knowledge and updating it based on observed data. Such a framework offers a flexible and robust approach to detecting change points, and its applicability extends across diverse domains such as genetics, environmental monitoring, finance, and quality control.

Change points are defined as abrupt variations in the generative parameters of a data sequence. The detection of change points is a relevant problem in the analysis and prediction of time series. The application can be found in copy number variation detection [16], air quality control [17] and signal processing [18].

Among the methods available, the Bayesian approach is particularly appealing because it automatically captures the trade-off between model complexity (number of change points) and model fit. It also allows one to express uncertainty about the number and location of change points.

In this paper, we propose a novel approach for detecting change points in a Poisson process. We introduce conditionally specified priors and derive the posterior distribution of model parameters using the general bivariate distribution with gamma conditionals. Such prior distribution have also been used in the comparison of gamma scale parameters [19] and the estimation of incomplete data [20]. Although these prior distributions have been extensively used in Bayesian analysis for classical distributions such as the normal distribution, Pareto distribution, and linear regression [21], their application in the context of Poisson processes is novel.

The remainder of this is organised as follows. Section 2 includes a short review on change point techniques and the motivation. Section 3 provides design of our proposed model. Section 4 we introduce the general bivariate distribution with gamma conditionals as the prior distribution for the parameters of a Poisson change point model and discuss the full Bayesian analysis of the change point problem. The application of our methodology is illustrated using simulated and real data sets in Sect. 5. Finally, Sect. 6 concludes the paper and suggests future extensions to our proposed approach.

2 Time Series Change Point Detection Techniques

Analysing time series data is crucial in various domains such as finance, economics, environmental science, and healthcare as it allows for the detection of underlying patterns, trends, and anomalies. In this context, change point detection techniques play a vital role in identifying points in a time series where the statistical properties significantly change.

Change point detection methods aim to pinpoint abrupt or gradual shifts in the underlying characteristics of a time series, which may indicate changes in mean, variance, distribution, or other structural properties. Detecting change points is essential for understanding system behavior, forecasting future trends, and detecting unusual events or anomalies.

Numerous change point detection methods have been developed, each with its strengths and assumptions. Classic techniques include cumulative sum methods, likelihood ratio tests, and sequential analysis methods. More advanced approaches leverage Bayesian inference, nonparametric methods, and machine learning algorithms to detect change points in complex and high-dimensional time series data.

Chen and Gupta [22, 23] conducted a detailed study of parametric models for change point analysis, exploring the univariate and multivariate normal cases, regression models, exponential-type models, and models with discrete data, from both classical and Bayesian perspectives. They also presented applications in genetics, medicine, and finance.

The use of Bayesian techniques in these types of models is extensively studied in [24]. One popular Bayesian change point detection method is the Bayesian Online Change point Detection algorithm proposed by [25], which provides a probabilistic framework for online change point detection and has been widely applied in signal processing, finance, and environmental monitoring. Bootstrap techniques have also been used by various authors to estimate these types of problems, as highlighted by [26].

Modern machine learning approaches, such as deep learning models, have shown promise in change point detection. For instance, [27] present a Long Short-Term Memory based model for detecting change points in multivariate time series data, demonstrating its effectiveness in identifying shifts in complex temporal patterns. In another study [28] reviewed models for the detection of change points in time series, including supervised and unsupervised algorithms proposed in the literature, and propose suitable criteria for comparing these algorithms.

In time series trend analysis, [29] propose a solution for change point detection, assessing four methods: wild binary segmentation, E-agglomerative algorithms, iterative robust detection methods, and Bayesian analysis.

In this study, we propose a Bayesian approach for detecting change points in a Poisson process. Unlike previous studies, we assume that the parameters of the Poisson process before and after the change are jointly distributed. Therefore, we propose a joint conjugate prior distribution based on the conditional specification methodology and introduce the application of conditionally specified prior distributions in change point detection problems. The general aspects of conditional specification can be found in [30]. The following section provides the details of obtaining the proposed prior distribution.

3 Motivation and Design of the Model

The general ideal of the conditional specification methodology can be described as follows. Suppose \(x_i\), for \(i = 1, \dots , n\), be n independently distributed random variables with probability distribution functions of \(f(\theta _i)\), where \(\theta _i \in \Theta \subset {\mathbb {R}}^n\) and let likelihood function be denoted as

$$\begin{aligned}f(x_1, \dots , x_n| \theta _1, \dots , \theta _n). \end{aligned}$$

Our interest lies in specifying a class of conjugate prior distributions such that the conditional distribution of \(\theta _i|\theta _{-i}\) belongs to the family class of \(f(\theta _i|\theta _{-i})\), where \(\theta _{-i} = (\theta _1, \dots , \theta _{i-1}, \theta _{i+1}, \dots , \theta _n)\).

We consider a candidate family of prior distributions for \(\theta _1, \dots , \theta _n\) such that, for each i, the conditional density of \(\theta _i\) given \(\theta _{-i}\) belongs to the family \(f_i\). We will show that the posterior distribution will be in the same family and will also be conditionally specified, resulting in a broad and flexible conjugate prior family for \(\theta _1, \dots , \theta _n\).

Simulation from the posterior will be readily implemented using a Gibbs sampling algorithm. The Gibbs sampling can be implemented even when using conditional densities that are incompatible or only compatible with an improper joint density [31].

Now, let \(X_i\) be a Poisson random variable where \(i = 1, \dots , T\). Assume that the change point occurs at time k such that

$$\begin{aligned} x_i\sim {{{\mathcal {P}}}}o(\lambda ),\;\;i=1,2,\dots ,k, \end{aligned}$$

and

$$\begin{aligned} x_i\sim {{{\mathcal {P}}}}o(\alpha ),\;\;i=k+1,\dots ,n, \end{aligned}$$

where \(\lambda >0\), \(\alpha >0\) and \(k\in \{1,2,\dots ,n\}\) are unknown parameters and \(X\sim {{{\mathcal {P}}}}o(\lambda )\) denotes a Poisson distribution with parameter \(\lambda \). In can be seen if \(k=n\), then \(\lambda = \alpha \) and we do not have change. Thus, the likelihood function takes the form,

$$\begin{aligned} L(\lambda ,\alpha ,k)\propto \lambda ^{\sum _{i=1}^k x_i}\alpha ^{\sum _{i=k+1}^nx_i}\exp \left( -k \lambda - (n - k+1) \alpha \right) . \end{aligned}$$
(1)

Our goal is to obtain a conjugate prior for \(\lambda \) and \(\alpha \) in a way that if \(\alpha \) is known, a conjugate prior for \(\lambda \) is a gamma distribution, and if \(\lambda \) is known, the conjugate prior for \(\alpha \) is again a gamma distribution. Consequently, we have conjugate prior distributions for each parameter conditioned on the other parameter.

In order to obtain a bivariate conjugate distribution for \(\lambda \) and \(\alpha \), we will have to obtain the most general bivariate distribution whose conditional distributions are gamma. The class of distributions whose conditionals are gamma has been obtained in [30].

Let us assume the likelihood in Eq. (1) only depends on parameters \(\alpha \) and \(\lambda \). We assume parameter k is known. According to the Theorem 1 in [32], the most general bivariate distribution with all conditionals of \(\lambda \) given \(\alpha \) and, of \(\alpha \) given \(\lambda \), being gamma distribution has the following form

$$\begin{aligned} \pi (\lambda ,\alpha ;\varvec{m})\propto & {} (\lambda \alpha )^{-1}\exp [-m_{10}\lambda -m_{01}\alpha +m_{20}\log \lambda +m_{02}\log \alpha \nonumber \\{} & {} +m_{11}\lambda \alpha -m_{12}\lambda \log \alpha -m_{21}\alpha \log \lambda +m_{22}\log \lambda \log \alpha ]. \end{aligned}$$
(2)

which is a conjugate prior for the family of likelihood given in (1). A bivariate distribution with joint pdf (2) will known as (general bivariate distribution with gamma conditionals) which is denoted by \((\lambda ,\alpha )\sim \mathcal{GBGC}(\varvec{m})\).

As can be seen in (2), the new class of distributions depends on eight parameters with the following conditional distributions are

$$\begin{aligned} \lambda |\alpha\sim & {} {{{\mathcal {G}}}}a(a_1(\alpha ),p_1(\alpha )), \end{aligned}$$
(3)
$$\begin{aligned} \alpha |\lambda\sim & {} \mathcal{G}a(a_2(\lambda ),p_1(\lambda )). \end{aligned}$$
(4)

It can be seen that the conditional distributions of the proposed conjugate prior also conjugate distributions for the parameters \(\lambda \) and \(\alpha \). Moreover, it is important to note that the model incorporates informative priors, allowing the incorporation of prior knowledge about the parameters. Lastly, due to the specific construction of the model, both conditional distributions follow a gamma distribution, which facilitates their estimation using Gibbs sampling algorithm. The conditional parameters in (3)–(4) are given by,

$$\begin{aligned} \begin{array}{rcl} a_1(\alpha )&{}=&{}m_{20}-m_{21}\alpha +m_{22}\log \alpha ,\\ p_1(\alpha )&{}=&{}m_{10}-m_{11}\alpha +m_{12}\log \alpha ,\\ a_2(\lambda )&{}=&{}m_{02}-m_{12}\lambda +m_{22}\log \lambda ,\\ p_2(\lambda )&{}=&{}m_{01}-m_{11}\lambda +m_{21}\log \lambda . \end{array} \end{aligned}$$
(5)

In order to ensure that this prior distribution is proper, the hyperparameters must satisfy the following list of constraints,

$$\begin{aligned} \begin{array}{rcl} &{}&{}m_{11}\le 0,\\ &{}&{}m_{12}\le 0,\\ &{}&{}m_{21}\le 0,\\ &{}&{}m_{22}\le 0,\\ &{}&{}m_{10}>m_{12}[1-\log (m_{12}/m_{11})],\\ &{}&{}m_{20}>m_{22}[1-\log (m_{22}/m_{21})],\\ &{}&{}m_{01}>m_{21}[1-\log (m_{21}/m_{11})],\\ &{}&{}m_{02}>m_{22}[1-\log (m_{22}/m_{12})]. \end{array} \end{aligned}$$
(6)

Note that for a gamma random variable Y with the probability function,

$$\begin{aligned} f(x;a,p)=\frac{p^ax^{a-1}e^{-px}}{\Gamma (a)},\;\;x\ge 0. \end{aligned}$$
(7)

the expected value and variance are \(E(Y)=\frac{a}{p}\) and \(var(Y)=\frac{a}{p^2}\), respectively.

3.1 A Relevant Submodel

Consider the bivariate continuous distribution with joint pdf,

$$\begin{aligned} f(\lambda ,\alpha )=\frac{k_{r,s}(\phi )m_1^rm_2^s}{\Gamma (r)\Gamma (s)}\lambda ^{r-1}\alpha ^{s-1}e^{-m_1\lambda -m_2\alpha -\phi m_1m_2\lambda \alpha },\;\;\lambda ,\alpha \ge 0 \end{aligned}$$
(8)

where \(r,s,m_1,m_2>0\) and \(\phi \ge 0\), which is a submodel of (2) with a new parameterization (see [30]). A random variable with joint probability density function (8) will be denoted by,

$$\begin{aligned} (\lambda ,\alpha )\sim \mathcal{BGC}(r,s,m_1,m_2,\phi ) \end{aligned}$$
(9)

The conditional distributions are:

$$\begin{aligned} \lambda |\alpha\sim & {} {{{\mathcal {G}}}}a(r,m_1(1+\phi m_2\alpha )), \end{aligned}$$
(10)
$$\begin{aligned} \alpha |\lambda\sim & {} {{{\mathcal {G}}}}a(s,m_2(1+\phi m_1\lambda )). \end{aligned}$$
(11)

The marginal distributions of (8) are given by,

$$\begin{aligned} f_\lambda (\lambda )=\frac{k_{r,s}(\phi )m_1^r}{\Gamma (r)}\frac{\lambda ^{r-1}e^{-m_1\lambda }}{(1+\phi m_1\lambda )^s},\;\;\lambda >0 \end{aligned}$$
(12)

and

$$\begin{aligned} f_\alpha (\alpha )=\frac{k_{r,s}(\phi )m_2^s}{\Gamma (s)}\frac{\alpha ^{s-1}e^{-m_2\alpha }}{(1+\phi m_2\alpha )^r},\;\;\alpha >0 \end{aligned}$$
(13)

The normalizing constant is given by,

$$\begin{aligned} k_{r,s}(\phi )=\frac{\phi ^r}{U(r,r-s+1,1/\phi )}, \end{aligned}$$
(14)

where U(a, b, z) denotes the hypergeometric function, which is defined by (\(a,z>0\)),

$$\begin{aligned} \displaystyle U(a,b,z)=\frac{1}{\Gamma (a)}\int _0^\infty e^{-zt}t^{a-1}(1+t)^{b-a-1}dt \end{aligned}$$
(15)

[33].

The raw moments of the marginal distributions (12) and (13) are given by,

$$\begin{aligned} E(\lambda ^k)=\frac{\Gamma (r+k)k_{r,s}(\phi )}{\Gamma (r)k_{r+k,s}(\phi )m_1^k} \end{aligned}$$
(16)

and

$$\begin{aligned} E(\alpha ^k)=\frac{\Gamma (s+k)k_{r,s}(\phi )}{\Gamma (s)k_{r,s+k}(\phi )m_2^k} \end{aligned}$$
(17)

respectively.

4 Bayesian Analysis with GBGC Prior

Let us assign the joint distribution of \(\lambda \) and \(\alpha \)

$$\begin{aligned} (\lambda ,\alpha )\sim \mathcal{GBGC}(\varvec{m}^{(0)}), \end{aligned}$$

as a prior distribution and incorporate Eq. (2) with (1). Thus, we obtain the following posterior distribution

$$\begin{aligned} (\lambda ,\alpha )|x\sim \mathcal{GBGC}(\varvec{m}^{*}), \end{aligned}$$

where the hyperparameters vector \(\varvec{m}^{(0)}\) is updated to \(\varvec{m}^{*}\) using the expression in Table 1. Note that only four of the eight parameters are updated by data. The rest of the parameters do no change. However, the existence of these parameters permits more flexibility when we select the prior distribution.

Table 1 Hyperparameter updating of the prior (2) with likelihood (1)
Full size table

Now, if we consider the submodel

$$\begin{aligned} (\lambda ,\alpha )\sim \mathcal{BGC}(r^{(0)},s^{(0)},m^{(0)}_1,m^{(0)}_2,\phi ^{(0)}) \end{aligned}$$
(18)

and we combine with (2) we obtain

$$\begin{aligned} (\lambda ,\alpha )|x\sim \mathcal{BGC}(r^{(*)},s^{(*)},m^{(*)}_1,m^{(*)}_2,\phi ^{(*)}) \end{aligned}$$
(19)

where the parameters are updated according to Table 2

Table 2 Hyperparameter updating of the prior (8) with likelihood (1)
Full size table

4.1 Parameter Estimation

In the conditional context, Gibbs sampling is a natural estimation methodology. The idea in Gibbs sampling is to generate posterior samples by sweeping through each variable (or block of variables) to sample from its conditional distribution with the remaining variables fixed to their current values. Assume that we are interested in approximating the posterior moments of a given function of \(\lambda \) and \(\alpha \), say \(\delta (\lambda ,\alpha )\).

Then, to approximate \(E(\delta (\lambda ,\theta )|x)\), we generate random values

$$\begin{aligned} \lambda _1,\alpha _1,\lambda _2,\alpha _2,\dots ,\lambda _{m_0+m},\alpha _{m_0+m} \end{aligned}$$

using the conditional gamma distributions,

$$\begin{aligned} \lambda |(\alpha ,x)\sim & {} {{{\mathcal {G}}}}a(a_1(\alpha ),p_1(\alpha ))\\ \alpha |(\lambda ,x)\sim & {} {{{\mathcal {G}}}}a(a_2(\lambda ),p_2(\lambda )), \end{aligned}$$

where the expressions for obtaining \(m_{ij}\) are given in Table 1 and \(m_0\) is the number of iterations before burn-in. Thus, we have the estimator,

$$\begin{aligned} E(\delta (\lambda ,\alpha )|x)\approx \frac{1}{m}\sum _{i=m_0+1}^{m_0+m}\delta (\lambda _i,\alpha _i). \end{aligned}$$

At each iteration l, for \(l = 1, \dots , M\), the following steps are repeated:

  1. (1)

    Set \(l = 0\) and initial values as \(\lambda ^{(0)}, \alpha ^{(0)}\) and \(k^{(0)}\).

  2. (2)

    Repeat for \(l = 1, \dots , M\)

    1. (a)

      Draw \(\lambda ^{(l)}|(\alpha ^{(l-1)}, k^{(l-1)})\) from \({{{\mathcal {G}}}}a(a_1(\alpha )^{(l-1)}, b_1(\alpha )^{(l-1)};k^{(l-1)})\).

    2. (b)

      sample from \(\alpha ^{(l)}|(\lambda ^{(l)}, k^{(l-1)})\) from \({{{\mathcal {G}}}}a(a_2(\lambda ^{(l)}), b_2(\lambda ^{(l)});k^{(l-1)})\).

    3. (c)

      sample from \(k^{(l)}|(\lambda ^{(l)}, \alpha ^{(l)})\) from \(\pi (k|\lambda ^{(l)}, \alpha ^{(l)})\).

where \(\pi (k|\lambda ^{(l)}, \alpha ^{(l)})\) is the conditional posterior distribution of k given in (20). Let us assume \(k\sim unif\{1,n\}\) then k can be updated using its posterior conditional distribution

$$\begin{aligned} \pi (k^{(l)}|x, \lambda ^{(l)},\alpha ^{(l)}) = \frac{\exp \Big [k^{(l)}(\alpha ^{(l)} - \lambda ^{(l)})\Big ]\big (\frac{\lambda ^{(l)}}{\alpha ^{(l)}}\big )^{S_{k^{(l)}}}}{\sum _{j = 1}^{n} \exp \Big [j(\alpha ^{(l)} - \lambda ^{(l)})\Big ]\big (\frac{\lambda ^{(l)}}{\alpha ^{(l)}}\big )^{S_{j}}}, \end{aligned}$$
(20)

where \(m^{\text{ th }}\) iteration, for \(m = 1, \dots , M\), and \(S_k\) is \(\sum _{i = 1}^{k} x_i\) [34]. As a previous step, we must elicit the hyperparameters \(m_{ij}\) using the methods proposed in Sect. 4.2.

4.2 Hyperparameter Elicitation

This section provides a brief description of eliciting hyperparameters. Similar to Arnold01, we consider inconsistency in the prior information provided by the expert or experts. This will allow us to assume a sample space for the conditional conjugate space rather than exactly one value that agrees with the prior information elicited from our expert or experts.

Let \(\mu \), \(\sigma ^2\), \(\mu '\) and \(\sigma '^2\) denote the conditional mean and variance of \(\lambda |\alpha \) and \(\alpha |\lambda \), respectively. We assume a series of \(\alpha _1, \dots , \alpha _{m_1}\) and \(\lambda _1, \dots , \lambda _{m_2}\) based on the experts’ information are available. This results in a system of equations will allow us to obtain a realisation of hyperparametrs.

$$\begin{aligned} \mu _j&= E(\lambda |\alpha = \alpha _j)\nonumber \\ \sigma ^2_j&= Var(\lambda |\alpha = \alpha _j) \quad j = 1, \dots , m_1, \end{aligned}$$
(21)
$$\begin{aligned} \mu '_i&= E(\alpha | \lambda = \lambda _i)\nonumber \\ \sigma '^2_i&= Var(\alpha |\lambda = \lambda _i) \quad i = 1,\dots , m_2 \end{aligned}$$
(22)

In order to satisfy conditions in Eq. (6) sequential quadratic programming using nloptr [35] in R was used to solve the above system of equations and elicit hyperparameters. Sequential Quadratic Programming (SQP) is one of the most successful methods for the numerical solution of constrained nonlinear optimization problems. It relies on a profound theoretical foundation and provides powerful algorithmic tools for the solution of large-scale technologically relevant problems.

5 Numerical Experiments

The numerical experiments is designed as follows. The method will be applied to sets of simulated data and real data. The simulation study investigated the performance of the model under three cases: 1. all parameters of the model are fixed, 2. varying k, 3. varying n and k. In all examples, 100 sets of data are simulated and number of iterations are 20,000. Based on Gelman-Rubin convergence diagnostics [36, 37], chains were considered to be converging after 5000 iterations, in all simulations. The accuracy of parameter estimates using root mean square error (RMSE).

The real data application will use the well known mine data available in R.

5.1 Simulation Study

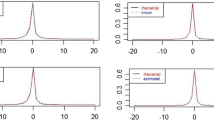
Trace plots and marginal posterior density of model parameters for the full model and the submodel are presented in.

From Table 2, it can be seen that model is not generally affected by the number of observations and where the change happens.

Finally, we extended the simulation study to sets of MC simulation studies for \(N = 10000\) and obtained the RMSE for the parameters of the model. In order to present the convergence diagnostics, we selected Figs. 3 and 4 as examples of the Gelman-Rubin convergence diagnostics plots which confirm the convergence after 5000 burn-in [38].

5.1.1 Case 1: \(n = 200, k = 100, \lambda = 1\) and \(\alpha = 3\)

Case 1 simulates data from a model with \(\lambda = 1, \alpha = 3, n = 200\) and \(k = 100\). A realisation of the conditional posterior distributions of model parameters was obtained using Gibbs sampler, and graphical presentation of the results including trace plots, marginal posterior densities and Gelman–Rubin diagnostics plot are given in Figs. 6–4.

It can be seen for both models the posterior mean of parameters are close to true values. However, the posterior variance for parameters \(\lambda \) and \(\alpha \) were small.

Fig. 1
figure 1

Monte Carlo simulation results of the full model

Full size image
Fig. 2
figure 2

Monte Carlo simulation results of the sub-model

Full size image
Fig. 3
figure 3

Gelman–Rubin diagnostics plots and statistics for parameters a \(\lambda \), b \(\alpha \) and c k of the full model with \(n = 200\) and \(k = 100\). The Gibbs sampler converges after 5000 iterations

Full size image
Fig. 4
figure 4

Gelman–Rubin diagnostics plots and statistics for parameters a \(\lambda \), b \(\alpha \) and c k of the sub-model model with \(n = 200\) and \(k = 100\). The Gibbs sampler converges after 5000 iterations

Full size image

5.1.2 Case 2: \(n = 200, \lambda = 1\), \(\alpha = 3\) and \(k = 50, 100, 150\)

The simulation study was extended where \(\lambda \), \(\alpha \) and n are fixed with values of 1, 3 and 200, respectively and k varies at 25%, 50% and 75% of the total number of observations. This will allow us to assess the performance of the model based on where the change happens.

Results for this case are summarised in Table 3. It can be seen k has hardly been affected by the position of change. However, the estimation of parameters \(\lambda \) and \(\alpha \) was less accurate when the location of change was at the 25% of the total sample size for both full- and sub-model.

Table 3 Posterior mean (sd) for single Gibbs sampler of the full model and sub-model with \(n = 200\), \(M = 15000\) after 5000 burnin where change happens at \(k = 25\%, 50\%\) and \(75\%\)
Full size table

5.1.3 Case 3: \(\lambda = 1\) and \(\alpha = 3\), varying n and k

In the final case we assessed the effect of sample size on the parameter estimation, in addition to the location of change. Data was simulated with values of \(n = 50, 100\) and 150. Tables 4 and 5 provide summarise performance of full- and sub-models using RMSE.

Table 4 Residual mean square error (RMSE) of the full model, where the number of observations \(N={50,100,150}\) and change points happening at the following percentages \(25\%,50\%,75\%.\)
Full size table
Table 5 Residual mean square error (RMSE) of the sub model, where the number of observations \(N={50,100,150}\) and change points happening at the following percentages \(25\%,50\%,75\%.\)
Full size table

5.2 Real Data: Coal Mine Example

The coal mine example adopted from [39]. The data was downloaded from the boot library in R [40]. The data set provided the dates of 191 explosions in coal mines which resulted in 10 or more fatalities between March 15, 1851 and March 22, 1962.

Fig. 5
figure 5

Mine data adopted from Davison and Hinkley (1997) illustrates number of explosions with more than 10 mortalities from 1851 to 1962

Full size image

Let the number of explosions with more than 10 mortalities, X such that

$$\begin{aligned} x_i\sim & {} Po(\lambda ), \; i = 1, \dots , k\\ x_i\sim & {} Po(\alpha ), \; i = k+1, \dots , 191. \end{aligned}$$

The full model was only fitted to the data. In order to solve the system of equations in (6)–(5) elicit hyperparameters, we assumed the following values for the conditional expected mean and variances

$$\begin{aligned}&\mu _1 = E(\lambda |\alpha ) = 0.038, \sigma _1^2 = Var(\lambda |\alpha )= 0.00012\\&\mu _2 = E(\lambda |\alpha ) = 0.038, \sigma _2^2 = Var(\lambda |\alpha )= 0.00011\\&\mu _3 = E(\alpha |\lambda ) = 0.024, \sigma _3^2 = Var(\alpha |\lambda )= 0.00012\\&\mu _4 = E(\alpha |\lambda ) = 0.024, \sigma _4^2 = Var(\alpha |\lambda )= 0.000073 \end{aligned}$$

Therefore, under the general model hyperparameters can be elicited as illustrated in Table 6.

Table 6 Hyperameters for the full modell in the mine data example
Full size table

Table 7 provides a summary of the posterior mean, standard deviation and \(95\%\) credible intervals (CI) of the model parameters. The results are compared with a basic model where we assume \(\lambda \) and \(\alpha \) are independently distributed with non-informative gamma priors. It can be seen that although both models have close posterior means, the proposed model offers smaller standard deviation and a narrower \(95\%\) CI.

Table 7 Posterior mean (sd) and 95% credible intervals (C.I.) for parameters of the full model for the min data example
Full size table
Fig. 6
figure 6

Mine data Gibbs sampler chain results, where a, c and e are the chain convergence plots for the parameters \(\lambda \),\(\alpha \) amd k

Full size image

Trace plots and marginal density plots are presented in Fig. 6. Finally, the posterior mean of the model parameters were added to the coal mine data along with the estimated change point and presented in Fig. 7. It can be seen that the number of explosions resulting in 10 or more mortalities have decreased around year 40 which is 1891.

Fig. 7
figure 7

Mine data along with the posterior mean of \(\lambda \) and \(\alpha \) presented in yellow

Full size image

6 Conclusions

In this paper, we presented a novel approach for estimating change point problems by using a broad class of conjugate prior distributions derived from a conditional specification methodology. While previous research extensively demonstrated the application of such prior distributions in problems involving continuous distributions, our contribution lied in exploring their effectiveness in the context of discrete distributions, specifically the Poisson process.

We conducted a comprehensive simulation study and applied the proposed methodology to real mine data. Through Gelman-Rubin diagnostics, we confirmed the convergence of the Gibbs sampler after a burn-in period of 5000 iterations. The simulation results revealed that parameter estimates exhibit smaller error when the change point, denoted as k, is closer to half of the total data points n. We compared the results obtained using our methodology with those of a basic model assuming independent parameters with non-informative priors. The findings demonstrated that our proposed approach yields significantly smaller estimation errors.

Furthermore, our methodology holds potential for extension to estimate multiple change points. Additionally, the introduction of a bivariate Poisson process poses new challenges that warrant further investigation and refinement of our proposed methodology. Overall, our research contributes to the advancement of change point analysis and provides valuable insights for improving the estimation accuracy in various application domains.