Abstract
Most decision making methods used to evaluate a system or demonstrate the weak and strength points are based on fuzzy sets and evaluate the criteria with words that are modeled with fuzzy sets. The ambiguity and vagueness of the words and different perceptions of a word are not considered in these methods. For this reason, the decision making methods that consider the perceptions of decision makers are desirable. Perceptual computing is a subjective judgment method that considers that words mean different things to different people. This method models words with interval type-2 fuzzy sets that consider the uncertainty of the words. Also, there are interrelations and dependency between the decision making criteria in the real world; therefore, using decision making methods that cannot consider these relations is not feasible in some situations. The Decision-Making Trail and Evaluation Laboratory (DEMATEL) method considers the interrelations between decision making criteria. The current study used the combination of DEMATEL and perceptual computing in order to improve the decision making methods. For this reason, the fuzzy DEMATEL method was extended into type-2 fuzzy sets in order to obtain the weights of dependent criteria based on the words. The application of the proposed method is presented for knowledge management evaluation criteria.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Many decision making methods are being proposed to facilitate the decision making process. Decision making problems consist of several criteria, and each criterion is evaluated by some other subcriteria. The evaluation criteria are almost dependent based on the complexity and vagueness of the real world. Therefore, decision making methods that consider these interrelations between criteria are more desirable. The Decision-Making Trail and Evaluation Laboratory (DEMATEL) was proposed by the Battelle Memorial Institute through its Geneva Research Centre (Gabus and Fontela 1973). This method considers the causal relationships between criteria and illustrates the weights between criteria by diagraphs.
Lin and Wu (2004) proposed a fuzzy extension of the DEMATEL method. The judges are based on linguistic variables and triangular fuzzy numbers, and the final weights of criteria are crisp numbers. In their approach all decision makers used a specified linguistic variable that may have different meanings for them based on the vagueness of each word. Words mean different things to different people, so they are uncertain (Mendel and Wu 2010). After Zadeh (1965) introduced a fuzzy set theory to deal with vague problems, in which linguistic labels have been used within the framework of the fuzzy set theory. After he introduced the type-2 fuzzy sets (T2 FSs), the first concept of the fuzzy set was renamed to type-1 fuzzy sets (T1 FSs) (Zadeh 19651975). The main difference between these two types is that the memberships of T1 FSs are crisp numbers, whereas the membership functions of T2 FSs are T1 FSs. The latter type has a sense of uncertainty. Zadeh (1999) proposed the paradigm of computing with words based on the T2 FSs that is a methodology in which the objects of computation are words and propositions drawn from a natural language. Mendel (200120022007) proposed the framework for perceptual computing based on computing with words. Words were the enabler of the perceptual computer; therefore, it could consider the uncertainty related to each word based on interval type-2 fuzzy sets (IT2 FSs). However, in perceptual computing, criteria were considered independent.
Therefore, the aim of this study was the IT2 FS extension of the DEMATEL method in order to obtain the criteria's weights based on the words. For this reason, perceptual computing was combined with the DEMATEL method to overcome the problem of interrelations between criteria in perceptual computing. The weights obtained from this study can be further used in perceptual computing judgments. The rest of this paper is organized as follows: In the ‘Type-1 fuzzy DEMATEL method’ section, we described the concepts of fuzzy DEMATEL. In the ‘Interval type-2 fuzzy sets used in perceptual computing’ section, a background about the IT2 FSs used in perceptual computing is represented. The IT2 FS extension of DEMATEL is proposed in the ‘IT2 FSs DEMATEL method’ section. In the ‘Application of proposed method in defining weights for dependent criteria’ section, an empirical study is illustrated to demonstrate that the proposed method is useful. Discussions are presented in the next section, and the conclusion is presented in the last section.
Type-1 fuzzy DEMATEL method
The DEMATEL method had been used successfully in many decision making problems. Also, many researchers used this method in combination with another multicriteria decision analysis (MCDM) method. For example, Jassbi et al. (2011) used the fuzzy DEMATEL method for modeling the cause and effect relationship of strategy map. Chang et al. (2011) used the fuzzy DEMATEL method for developing supplier selection criteria. Yang and Tzeng (2011) proposed a combined MCDM model based on DEMATEL and analytic network process (ANP). Also, Chen and Chen (2010) used DEMATEL, fuzzy ANP, and TOPSIS for evaluating innovation performance in Taiwanese higher education institutes.
Lin and Wu (2004) proposed their fuzzy DEMATEL method as a stepwise procedure:
-
1.
Step 1: Identify the decision goal and form a committee.
-
2.
Step 2: Develop evaluation criteria and design the fuzzy linguistic scale. Lin and Wu ( 2004 ) used fuzzy triangular numbers to propose the fuzzy DEMATEL method. They used five linguistic terms as {very high influence, high influence, low influence, very low influence, no influence}. These linguistic terms are shown in Table 1.
-
3.
Step 3: Acquire and average the assessments of P decision makers. Every decision maker is asked to make pair-wise relationships between each pair of objects. Therefore, P fuzzy matrices with triangular fuzzy numbers are obtained that show the pair-wise comparison of the objects based on the decision makers' perceptions. Equation 1 is then used to calculate the average matrix :
(1)
The fuzzy matrix is called the initial direct-relation fuzzy matrix as shown in Equation 2:
In this matrix, are triangular fuzzy numbers, and will be regarded as triangular fuzzy number (0, 0, 0) whenever is necessary (Jassbi et al. 2011).
-
4.
Step 4: Normalizing initial direct-relation fuzzy matrix by Equation 4. The linear scale transformation is used as a normalization formula to transform the criteria scales into comparable scales ( Lin and Wu 2004 ). Suppose shows each triangular fuzzy number in each cell of and suppose that r is the maximum summation of the third element of each triangular fuzzy number in each row in Equation 3. As in the crisp DEMATEL method, Lin and Wu ( 2004 ) assumed at least one i (1 ≤ i ≤ n) such that . They claimed that this assumption is well satisfied in practical cases:
Let and define three crisp matrices, whose elements are extracted from , as follows:
-
5.
Step 5: Compute total-relation fuzzy matrix . Matrix was computed in the previous step. Based on the crisp DEMATEL method, total-relation fuzzy matrix can be computed through Equation 6:
(6)
The elements of matrix contain triangular fuzzy numbers as shown in Equation 7:
After acquiring matrix , the next step is to calculate the and , where and are the sum of the rows and the sum of the columns of (Lin and Wu 2004). To acquire the importance of the criteria and understand the causal relationship between criteria, and should be defuzzified. The shows the relative importance of criterion i, and the demonstrates the causal relationship. If the value of is positive, the criterion belongs to the cause group, and if the value of is negative, the criterion belongs to the effect group.
Interval type-2 fuzzy sets used in perceptual computing
The fuzzy extension of the DEMATEL method used linguistic terms for generating the initial direct-relation matrix. Therefore, decision makers are asked to compare the decision making criteria based on the codebook of words, e.g., Table 1. Zadeh (1999) proposed the paradigm of computing with words based on the T2 FSs that is a methodology in which the objects of computation are words and propositions drawn from a natural language. Computing with words is fundamentally different from the traditional expert systems which are simply tools to realize an intelligent system, but are not able to process natural language which is imprecise, uncertain, and partially true. As mentioned before, words mean different things to different people, so they are uncertain. Words in computing with words are modeled by T2 FSs that can model more uncertainties (Mendel and Wu 2007). Mendel and Wu (2010) used computing with words for making subjective judgments which was called perceptual computing. A perceptual computer consists of three parts: encoder (using interval approach (IA)), linguistic weighted average (LWA) engine, and decoder (Mendel 200120022007). Each part of the perceptual computer was utilized in the IT2 FS extension of the DEMATEL method.
In order to obtain an IT2 FS model for a word, IA was proposed by Mendel and Wu (2008). This approach had been referred to as T2 fuzzistics (Mendel 2007). In this approach, all decision makers (i = 1, 2,…, n) provide the end points of an interval associated with a word. The intervals need to be between 0 and 10. The mean and standard deviation are then computed for the end points. The intervals show the level of uncertainty associated to each word. This approach maps each evaluator's data interval into a prespecified T1 membership function (MF) and interprets the latter as an embedded T1 FS of an IT2 FS.
In this section mathematical definitions of IT2 FS are presented that is used in the rest of the paper.
An is characterized by the MF , where x ∈ X and u ∈ J x ⊆ [0, 1], that is (Mendel and Wu 2010),
Equation 8 can be expressed as (Mendel 2001;Mendel and John 2002)
where x is called the primary variable with the domain of X. J x ⊆ [0, 1] is the primary membership of x, u is the secondary variable, and is the secondary MF at x. Note that Equation 9 means . Uncertainty about is conveyed by the union of all of the primary memberships, called the footprint of uncertainty of , i.e., (Wu and Mendel 2007)
An IT2 FS is shown in Figure 1. The FOU is shown as the shaded region. It is bounded by an upper MF (UMF), , and a lower MF (LMF), , both of which are type-1 fuzzy sets; consequently, the membership grade of each element of IT2 FS is an interval . It is also customary to use and for the LMF and UMF of (Mendel and Wu 2010):
so can also be expressed in terms of its vertical slices as
For discrete universe of discourse X and U, the embedded type-1 fuzzy set A e has N elements, one each from Jx 1, Jx 2,…, J xN , namely u1, u2,…, u N , i.e., (Wu and Mendel 2007)
The UMF and LMF of are two type-1 MFs that bound the FOU. is associated with the upper bound of and is denoted , ∀ x ⊆ X, and is associated with the lower bound of and is denoted , ∀ x ∈ X, that is,
UMF contains four digits and LMF contains five digits, of which the fifth parameter is its height. Let and be the perfectly normal IT2 FN based on Equation 11 (Hamrawi and Coupland 2009;Kaufmann and Gupta 1985), and then according to Wu and Mendel (2008),
where ° = {+, -, ×, ÷}.
IT2 FS DEMATEL method
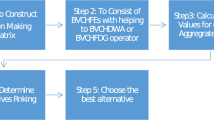
The procedure of developing the DEMATEL method by IT2 FSs is as follows:
-
1
Step 1: Identify the decision goals, criteria, and group of experts.
-
2
Step 2: Develop linguistic codebooks for decision making. In this step a codebook is designed, and decision makers are asked to define the interval end points for each word in the codebook. The codebook has the same words as in Table 1. Therefore, the codebook of words contains ‘very high influence’ , ‘high influence’ , ‘low influence’ , ‘very low influence’ , and ‘no influence’ . The IA is used to map these intervals into IT2 FSs ( Mendel and Wu 2008 ). The DEMATEL method does not consider the difference between the levels of expertise for each expert, but in this paper we developed another codebook that considers the level of expertise for each expert. This codebook contains three words (low, moderate, and high) ( Mendel and Wu 2007 ). Also, it is possible to put equal weights to the level of expertise for each expert.
-
3
Step 3: Acquire and compute the linguistic weighted average of the assessments. To measure the weights and causal relations between the criteria C = {C i | i = 1, 2,…, n}, a group of p experts are asked to define the influence relation between criteria based on the codebooks in step 2. Therefore, p pair-wise comparison IT2 FSs matrices are obtained. LWA that was proposed by Mendel and Wu ( 2007 ) was used to generate the IT2 FS average matrix that is called initial-direct-relation IT2 FS matrix.
In the previous section, we used the IA to encode each word from the codebook to an IT2 FS. The output of the previous section is used to activate the LWA. Each decision maker used a word from the codebook to transfer the influence of each criterion on another one. Each decision maker had a level of expertise that was assigned to him/her from a codebook of expertise weights that contained three words: ‘low,’ ‘moderate,’ and ‘high.’ Decision makers were asked to define the end points of an interval on the scale of 0 to 10 for each word in the codebook. Then the IA is used to encode the intervals into IT2 FSs. The LWA maps IT2 FSs into IT2 FSs. This method is based on the weighted average that is the most widely used form of aggregation.Suppose k is the number of decision makers (k = 1, 2,…, p) and is ij th entry of initial-direct-relation IT2 FS matrix . The LWA matrix can be obtained from Equation 17:
-
4
Step 4: Establish the normalized initial-direct-relation matrix.
Let , and and , of which the fifth element is its height. Therefore, can be defined by nine matrices, whose elements are crisp numbers (Liu and Mendel 2008):
Z d contains the forth element of . All are normal IT2 FSs; therefore, Z d contains the greatest elements in the initial-direct-relation matrix. The normalized direct-relation matrix can be defined as
Note that the fifth element of (height) is normalized between 0 and 1; therefore, there is no need to normalize this element.
-
5
Step 5: Compute the total-relation IT2 FS matrix .
To compute the total-relation IT2 FS matrix , we have to ensure the convergence of . The elements of are also IT2 FSs. can be defined by nine matrices, and the elements of these matrices are all crisp numbers.
Theorem 1. Let
and further define eight matrices. There is no need to consider the ninth matrix that contains the heights of.
Proof. The proof is straightforward; all the eight matrices contain crisp values, and the matrix multiplication is used to prove this theorem.
Lin and Wu (2004) proved and based on for triangular fuzzy sets. We used this theorem for IT2 FS matrix . Therefore, and based on and . Then the total-relation matrix is acquired as follows:
To acquire the importance weight of each criterion, we calculated , where shows the sum of the rows and shows the sum of the columns of the total-relation matrix and can be obtained through Equations 20 and 21:
Note that in Equations 20 and 21, t ij , i, j = 1, 2,…, n are IT2 FS, and their addition must be based on Equation 16.
-
6
Step 6: Decode each IT2 FS into a word.
In the previous step, we calculated the weights for each criterion, but these weights are IT2 FSs and must be decoded into words. This process is called the decoder. The IT2 FSs obtained from the previous step were decoded into seven words: ‘extremely low,’ ‘very low’ , ‘low’ , ‘fair’ , ‘high’ , ‘very high’ , and ‘extremely high’ . A decoding codebook is needed to store the FOUs for these seven words. Therefore, IA is used to map the intervals collected from the group of decision makers into IT2 FSs. In order to get the criteria weights based on the words in the codebook, the decoder must compare the similarity between two IT2 FSs so that the output of step 5 can be mapped into its most similar word in the codebook. These weights that are based on the words can be further used in the evaluation based on perceptual computing. Several similarity measures are introduced for IT2 (Bustince 2000;Gorzalczany 1987;Mitchell 2005;Wu and Mendel 20082009). In this study we used the Jaccard similarity measure for IT2 FSs. This approach uses average cardinality. Equation 22 is used to calculate the Jaccard similarity measure for IT2 FSs.
To decode the IT2 FSs obtained from , IT2 FSs must be mapped into [0,10]. For this reason, we used the min-max normalization method defined in Equation 23:
In this approach we acquired the criteria weights based on the interrelations between criteria. Further, these weights can be used for evaluation based on the perceptual computing method. The weights used in perceptual computing were independent, but this study helped to extend perceptual computing using dependent criteria and defining weights for each of them.
Application of proposed method in defining weights for dependent criteria
We used the proposed method to define weights of criteria that were used to evaluate the knowledge management capability of organization.
-
1
Step 1: Identify the decision goals, criteria, and group of experts.
For evaluating the knowledge management capability of organization based on perceptual computing, we had to define the weights for each criterion. Perceptual computing considers each criterion independent from the others. For this reason, the DEMATEL method was used to define the weights for criteria that were dependent and had interrelations. A group of three knowledge management experts were asked to compare the criteria. Six criteria were chosen for this reason including vision for change, culture, structure, infrastructure, support for change, and knowledge management processes.
-
2
Step 2: Develop linguistic codebooks for decision making.
The codebook of words that was used for comparing the influence of criteria on each other contained ‘very high influence,’ ‘high influence,’ ‘low influence,’ ‘very low influence,’ and ‘no influence.’ The IA is used to map these intervals into IT2 FSs. The FOUs for each word are presented in Table 2, and also, Figure 2 depicts the FOUs for the five words in the codebook.
The codebook used for the expertise weight is shown in Table 3. This codebook contains three words (low, moderate, high).
-
3
Step 3: Compute the linguistic weighted average of the assessments.
To measure the weights of each criterion based on the interrelationship between the six criteria, three knowledge management experts were asked to compare the criteria based on the codebook defined in Table 2. Therefore, three pair-wise comparison matrices are obtained. Table 4 shows the relative comparison matrix for one of the decision makers based on the codebook defined in Table 2. The average of these three matrices is obtained from LWA using Equation 17. To compute the LWA mentioned in Equation 17, decision makers' expertise weights should be defined. In this study we assume the equal expertise weights (‘moderate’) for the decision makers. The weights for decision makers' expertise are shown in Table 3. The result of LWA is initial direct-relation matrix that is shown in Table 5.
-
4
Step 4: Establish the normalized initial-direct-relation matrix.
We used Equation 18 to normalize the initial direct-relation IT2 FS matrix. The result is shown in Table 6.
-
5
Step 5: Compute the total-relation IT2 FS matrix .
Equation 19 was used to compute the total-relation IT2 FS matrix . The result is shown in Table 7. can be computed from Equations 21 and 22. Table 8 shows the result of for each criterion's nine numbers. Each set of nine numbers shows an interval type-2 fuzzy set that can be drawn and also can be decoded to a codebook of words.
-
6
Step 6: Decode each IT2 FS into a word.
The weights for each criterion were calculated in step 5 based on interval type-2 fuzzy sets. These weights can further be used in perceptual computing without decoding them to words. In addition, the weights can be decoded to words. The weight codebook was needed to decode the IT2 FSs obtained from step 5 into words. For this reason, a group of 30 people including the main decision makers in step 1 were asked to define end point intervals for the seven words in the codebook; then, the IA was used to map these intervals into IT2 FSs. The FOUs for the weight codebook are shown in Table 9. Also, Figure 3 depicts the FOUs for all seven words used for the weight codebook. As mentioned before, we used the Jaccard similarity measure to decode the FOUs obtained from the previous step into words from the weight codebook. In order to use the Jaccard similarity measure, should be normalized in [0,1]. For this reason, we used Equation 23. After normalizing , values of the Jaccard similarity measure can be used to decode the IT2 FSs weights into words based on the Jaccard similarity measure that is shown in Equation 22. The result of the decoder for each criterion is shown in the last column of Table 8.
Discussion
The purpose of this study was to extend DEMATEL and combine it with perceptual computing in order to consider the interrelations between weights in perceptual computing. According to the results, the IT2 FS extension of DEMATEL and the combination of perceptual computing and DEMATEL lead to the weights of evaluation criteria based on the codebook of words. Perceptual computing was used for decision making and subjective judgments. Words are the enabler of perceptual computing, and in this subjective judgment, IT2 FSs are used to model the words' uncertainty. In order to obtain the weights of dependent criteria, a codebook of words for evaluating the influence of criteria on each other was presented. We applied the proposed method to obtain the weights of criteria for knowledge management evaluation by perceptual computing. Decision makers were asked to associate the end points of intervals to each word. Then the intervals collected for each word were modeled into IT2 FSs with the use of the interval approach. The words used for defining the influences and their related IT2 FSs are shown in Table 2. Decision makers were asked to define the influence of criteria on each other through matrices. Three influence matrices are defined in this paper for six criteria. The difference between the fuzzy DEMATEL proposed by Lin and Wu (2004) and our approach is the effect of expertise weights on the aggregation of influence matrices. The linguistic weighted average was used to aggregate these matrices. The aggregated matrix was based on the level of expertise that contained IT2 FSs and is presented in Table 5. In order to decode the IT2 FSs into words, we used the Jaccard similarity measure. The result of the decoder for the six criteria is shown in Table 8. However, the IT2 FSs of weights could be decoded into crisp numbers, but we mapped IT2 FSs to words to use them further in perceptual computing evaluations. Also, other methods can be used to decode the IT2 FSs into decision classes of words (Mendel and Wu 2010).
Conclusions
To improve the interrelations between decision making criteria in perceptual computing, we proposed an interval type-2 fuzzy set extension of the DEMATEL method. In this method, we combined the perceptual computing characteristics with the fuzzy DEMATEL in order to map the influence matrices defined by words into weights. In perceptual computing, words are mapped into IT2 FSs. IT2 FSs are able to show the uncertainty related to each word in the codebook; therefore, they are suitable to model the uncertainty associated to decision making in the real word. The DEMATEL method considers the interrelations between criteria and defines weights based on these relations. Therefore, the combination of these two methods leads to a decision making method that can consider the uncertainty related to decision making and also the interrelations between criteria. The weights obtained from the proposed method can further be used for evaluation based on words. In order to define the cause and relation between criteria, the IT2 FSs should be defuzzified into crisp numbers. However, other decoding methods can be used to map the IT2 FS into words.
References
Bustince H: Indicator of inclusion grade for interval-valued fuzzy sets. Application to approximate reasoning based on interval-valued fuzzy sets. Int J Approx Reason 2000,23(3):137–209. 10.1016/S0888-613X(99)00045-6
Chang B, Chang C-W, Wu C-H: Fuzzy DEMATEL method for developing supplier selection criteria. Expert Syst Appl 2011, 38: 1850–1858. 10.1016/j.eswa.2010.07.114
Chen J-K, Chen I-S: Using a novel conjunctive MCDM approach based on DEMATEL fuzzy ANP, and TOPSIS as an innovation support system for Taiwanese higher education. Expert Syst Appl 2010, 37: 1981–1990. 10.1016/j.eswa.2009.06.079
Gabus A, Fontela E: Perceptions of the world problematique: communication procedure, communicating with those bearing collective responsibility (DEMATEL Report No. 1). Geneva: Battelle Geneva Research Centre; 1973.
Gorzalczany MB: A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Set Syst 1987, 21: 1–17. 10.1016/0165-0114(87)90148-5
Hamrawi H, Coupland S: Type-2 fuzzy arithmetic using alpha-planes. Proceedings of the IFSA-EUSFLAT conference, Lisbon, 20–24 July 2009 2009 edition. 2009.
Jassbi J, Mohammadnejad F, Nasrokkahzadeh H: A fuzzy DEMATEL framework for modeling cause and effect relationships of strategy map. Expert Syst Appl 2011, 38: 5967–5973. 10.1016/j.eswa.2010.11.026
Kaufmann A, Gupta M: Introduction to fuzzy arithmetic: theory and applications. New York: Van Nostran Reinhold; 1985.
Lin C-L, Wu W-W: A fuzzy extension of the DEMATEL method for group decision making. Eur J Oper Res 2004, 156: 445–455. 10.1016/S0377-2217(03)00020-1
Liu F, Mendel JM: Encoding words into interval type-2 fuzzy sets using an interval approach. IEEE Trans Fuzzy Syst 2008, 16: 1503–1521.
Mendel JM: Uncertain rule-based fuzzy logic systems: introduction and new directions. Upper-Saddle River: Prentice-Hall; 2001.
Mendel JM: An architecture for making judgments using computing with words. Int J Appl Math Comput Sci 2002,12(3):325–335.
Mendel JM: Computing with words and its relationship with fuzzistics. Inform Sci 2007, 177: 988–1006. 10.1016/j.ins.2006.06.008
Mendel JM, John RI: Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst 2002, 10: 117–127. 10.1109/91.995115
Mendel MJ, Wu D: Perceptual reasoning: a new computing with words engine. Proceedings of the IEEE international conference on granular computing, Silicon Valley, 2–4 Nov 2007, 446–451.
Mendel MJ, Wu D: Perceptual reasoning for perceptual computing. IEEE Trans Fuzzy Syst 2008,16(6):1550–1564.
Mendel MJ, Wu D: Perceptual computing: aiding people in making subjective judgments. Hoboken: Wiley-IEEE; 2010.
Mitchell HB: Pattern recognition using type-II fuzzy sets. Inform Sci 2005,170(2–4):409–418.
Wu D, Mendel JM: Aggregation using the linguistic weighted average and interval type-2 fuzzy sets. IEEE Trans Fuzzy Syst 2007, 15: 6.
Wu D, Mendel JM: Corrections to “Aggregation using the linguistic weighted average and interval type-2 fuzzy sets”. IEEE Trans Fuzzy Syst 2008, 16: 6.
Wu D, Mendel JM: A comparative study of ranking methods, similarity measures and uncertainty measures for interval type-2 fuzzy sets. Inform Sci 2009,179(8):1169–1192. 10.1016/j.ins.2008.12.010
Yang JL, Tzeng G-H: An integrated MCDM technique combined with DEMATEL for a novel cluster-weighted with ANP method. Expert Syst Appl 2011, 38: 1417–1424. 10.1016/j.eswa.2010.07.048
Zadeh LA: Fuzzy sets. Information and Control 1965, 8: 338–353. 10.1016/S0019-9958(65)90241-X
Zadeh LA: The concept of a linguistic variable and its application to approximate reasoning-I. Information Sciences 1975, 8: 199–249. 10.1016/0020-0255(75)90036-5
Zadeh LA: From computing with numbers to computing with words—from manipulation of measurements to manipulation of perceptions. IEEE Trans Circ Syst Fund Theor Appl 1999, 4: 105–119.
Acknowledgments
The authors would like to acknowledge the industrial relation department of K. N. Toosi University of Technology to make relations between the MAPNA Co. and the university available; and special thanks to the reviewers who helped improve this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
MBH carried out the presentation of a solution to address the shortcoming of perceptual computing considering the relationship between decision making criteria. MJT carried out the whole research idea and the validation and verification of the research outcomes. Both authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hosseini, M.B., Tarokh, M.J. Type-2 fuzzy set extension of DEMATEL method combined with perceptual computing for decision making. J Ind Eng Int 9, 10 (2013). https://doi.org/10.1186/2251-712X-9-10
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-9-10