Abstract
This paper considers a three-stage assembly flowshop scheduling problem with sequence-dependent setup times at the first stage and blocking times between each stage in such a way that the weighted mean completion time and makespan are minimized. Obtaining an optimal solution for this type of complex, large-sized problem in reasonable computational time using traditional approaches or optimization tools is extremely difficult. Thus, this paper proposes a meta-heuristic method based on simulated annealing (SA) in order to solve the given problem. Finally, the computational results are shown and compared in order to show the efficiency of our proposed SA.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Background
Because of strong competition and limitation of resources in our environment, scheduling is a very important decision-making process in production and service industries. In common flowshop scheduling, we have two main elements, namely a group of M machines and a set of N jobs to be processed on this group of machine [1]. Assembly flowshop scheduling is a type of flowshop that at first each of n jobs has to be processed at the first stage consisting of m different parallel machines and then assembled at the second stage including only one assembly machine [2]. Assembly-type production systems have evolved partially as an answer to the market pressure for larger product variety [3]. Most of studies considered a two-stage assembly flowshop scheduling problem (AFSP) defined as follows. M machines are available in the first stage and only one machine is available in the assembly stage. There are n jobs, which should be scheduled and each of them includes m + 1 operations. The first m operations of a job are performed at the first stage in parallel by m machines and the final operation is conducted at the second stage. Each of m operations of a job at the first stage is performed by a different machine, and the assembly operation on the machine at the second stage starts when all m operations at the first stage are completed. Each machine works just on one job at a time. It should be noted that when there is only one machine at the first stage [4]. In the two-stage AFSP, assumed collecting and transferring time of components from the first stage to assemble is negligible. This is unrealistic especially when a two-stage assembly problem is used to simulate production systems with a multi-facilities plant and a final assembly plant. But to have more realistic environments of a production system, it is required that the intermediate operation is devoted to collect and transport the manufactured parts from the various production areas to the assembly line. This stage is important especially when parts are manufactured in multiple production sites. The three-stage AFSP is the extended model of two-stage assembly flowshop that the collecting and transferring actions are regarded as the second stage, and assembly machine is in the third stage [3].
Suppose there are n jobs for scheduling, in which each job includes m components. At the first stage, there are m parallel and independent machines, in which each machine can process just one component. When all of m components of each job are processed on the first stage machines, they will be collected and transferred to the assembly machine (i.e., third stage) by passing the second stage (i.e., transportation stage). Then the machine at the third stage assembles m components of job that are transferred from the first stage together for completing a job. Koulamas and Kyparisis [3] proposed this type of an assembly line problem with the objective of minimizing the makespan. Hatami et al., [5] developed this model with sequence-dependent setup time for first stage machines.
In this paper, we consider a three-stage AFSP with blocking times and sequence dependent setup times. To make this type of assembly flowshop more realistic our research added the blocking times limitation (buffer = 0) to the model presented in [5]. Sequence-dependent setup time says that setup time of a job in position i on machine j depends on the current job and the previous job on this machine. Once its processing is completed on a processor in the first or second stage, a product is transferred directly to either an available processor in the next stage (or another downstream stage depending on the product processing route), or a buffer ahead of that stage when such an intermediate buffer is available. However, when an intermediate buffer is unavailable, the product remains blocking the processor until a downstream processor becomes available [6]. In general, blocking scheduling problems arise in modern manufacturing environments with limited intermediate buffers between processors, such as just-in-time production systems or flexible assembly lines, and those without intermediate buffers, such as surface mount technology (SMT) lines in the electronics industry for assembling printed circuit boards, which includes three different stages in the following sequence: solder printing, component placement and solder reflow [7].
Yokoyama and Santos [8] presented a branch-and-bound method for three-stage flowshop scheduling with assembly operations to minimize the weighted sum of product completion times where there is only one machine in each stage. Koulamas and Kyparisis [3] analyzed a three-stage assembly scheduling problem by minimizing the makespan and analyzed the worst-case ratio bound for several heuristics for this problem. Hatami et al., [5] extended the three-stage assembly flowshop model presented in [3] with sequence-dependent setup time by minimizing the mean flow time and maximum tardiness and they proposed two meta-heuristics, namely simulated annealing (SA) and tabu search (TS). Allahverdi and Al-Anzi [9] addressed a two-stage AFSP with setup time by minimizing the total completion time and they proposed a dominance relation and three heuristics, such as Ntabu, SDE and NSDE.
Lee et al., [10] studied a two-stage AFSP with considering two machines at the first stage. Al-Anzi and Allahverdi [4] considered a two-stage AFSP with the objective of minimizing the weighted sum of makespan and maximum lateness and presented heuristics namely TS, PSO, and SDE. Cheng et al., [11] studied two-stage differentiation flowshop consisting of a common critical machine in stage one and two independent dedicated machines in stage two by minimizing the weighted sum of machine completion times. Ng et al., [1] proposed a branch-and-bound algorithm for solving a two-machine flow shop problem with deteriorating jobs. Ruiz and Allahverdi [12] minimized the bi-criteria of makespan and maximum tardiness with an upper bound on maximum tardiness of the flowshop scheduling problem. Sun et al., [13] addressed powerful heuristics to minimize makespan in fixed, 3-machine, assembly-type flowshop scheduling.
In some environments, there are limited buffers or zero buffers between stages. Hall and Sriskandarajah [7] reviewed machine scheduling problems with blocking and no wait in process. Qian et al., [14] presented an effective hybrid algorithm based on deferential evolution (DE) for multi-objective flow shop scheduling with limited buffers. Liu et al., [15] solved flow shop scheduling with limited buffers with an effective hybrid PSO-based algorithm to minimize the maximum completion time. Wang et al., [16] introduced a hybrid genetic algorithm (GA) for flowshop scheduling with limited buffers with the objective to minimize the total completion time. Grabowski and Pempera [17] developed a fast tabu search (TS) algorithm to minimize the makespan in a flow shop problem with blocking.
Ronconi [18] analyzed the minimization of the makespan criterion for the flowshop problem with blocking by proposing constructive heuristics, namely MM, MME and PFE. Tavakkoli-Moghaddam et al., [6] presented an efficient memetic algorithm (MA) combined with (NVNS) to solve the flexible flow line with blocking (FFLB). Sawik [19] addressed a new mixed integer programming for the FFLB. Norman [20] explored a flowshop scheduling problem with finite buffer and sequence-dependent setup times and proposed a TS method. Ronconi and Henriques [21] introduced a GRASP-based heuristic method for a scheduling problem with blocking to minimizing the total tardiness. Tozkapan et al., [22] developed a lower bounding procedure and a dominance criterion incorporated into a branch-and-bound procedure for the two-stage AFSP to minimize the total weighted flowtime. Yagmahan and Yenisey [23] offered a multi-objective ant colony algorithm for flowshop scheduling to minimizing the makespan and total flow time. Sung and Kim [24] developed a branch-and-bound algorithm for two stage multiple assembly flowshop to minimize the sum of completion times. Yokoyama [25] considered flowshop scheduling with setup and assembly operation and to solve used pseudo-dynamic programming and a branch-and-bound. Liu and Kozan [26] studied scheduling flowshop with combined buffer condition considering blocking, no-wait and limited-buffer. Lee et al., [27] brought the concept of blocking into the deteriorating job scheduling problem on the two-machine flow- shop. They proposed A branch-and-bound algorithm incorporating with several dominance rules and a lower bound as well as several heuristic algorithms. Gong et al., [28] studied two-stage flow shop scheduling problem on a batching machine and a discrete machine with blocking and shared setup times. Wang et al., [29] proposed a HDDE algorithm for solving a flowshop scheduling with blocking to minimize the makespan.
Since blocking has been never considered in three-stage assembly flowshop so we add blocking as a constraint to the Hatami’s problem [5]. Thus according to the new objective functions (i.e., weighted mean completion time and makespan) and blocking, we present a new mathematical model for this case.
The rest of this paper is come up as follows. In the next section, we explain the new mathematical model. In Section 3, we propose a meta-heuristic method based on SA to solve the given problem. Section 4 discusses the computational results and finally, the conclusion is presented in Section 5.
Problem Description
The problem considered in this paper is a three-stage AFSP with sequence-dependent setup times at the first stage and blocking time between stages minimizing the weighted mean completion time. In this problem, there are n jobs available at zero time. Job preemption is not allowed and each job includes m parts or components. We have m independent parallel machines at the first stage and every part of a job should be processed on just one machine at the first stage and each machine can process only one part. Setup time of a job on machines depend on job and previous job. After completing all m parts of job at the first stage, if the next stage machine is available, they are collected and transferred by an automatic transportation system. We assume that transfer is done in the second stage. At the second stage and third stage, there is only one machine so each job needs to m + 2 operations to be completed. There is no buffer storage between stages so if the downstream machine is not available the job stays on the current machine and blocks, it will be available until the next stage.
Objective functions
By considering a scalarizing method, the bi-criteria problem is converted to a single objective problem. So, the objective function is computed by:
where, 0 < α < 1. Note that when α is equal to 0 or 1, the problem is reduced to the single criterion of C max or the weighted mean weighted completion time, respectively. The objective is to find a schedule which yields a minimum objective function value (OFV). In addition, we use the following notations in the presented model.
n: Number of jobs; m: Number of machines; e i,h : Starting time of job in position i at stage h; D i,h : Departure time of job in position i from stage h; t j,k : Processing time of job j on machine k at first stage; Si-1,i,k: Set up time on machine k from job in position i-1 to job i at the first stage; T i : Time of collecting and transferring job in position i to third stage; At i : Assembly time of job in position i; w j : Assigned weight to job j; C i,1 : Completion time of job j in position i at the end of first stage; C i,2 : Completion time of job j in position i at the end of second stage; C i : Completion time of job j in position i at the end of third stage; [C max ] = Cn: Completion time of job in last sequence; x i,j : If job j is in position i of sequence; x i,j = 1: otherwise, it is 0.
Mathematical model
Eq. (1) presents the objective function. Eqs. (2) and (3) show that each job can only be placed in one position and only one job can be placed in each position, respectively. Eqs. (4) and (5) express that processing of job in position i and will start at stage h when it is left the previous stage and the job in position i-1 has left stage h, respectively. Eq. (6) shows that the departure time of a job in position i at stage h-1 is after departure of the job in the previous sequence from stage h. Eq. (7) calculates blocking time of job in position i at stage h. Eq. (8) shows the departure time of a job in position i from stage h. Eqs. (9), to (11) calculate the completion time of a job in position i at the first, second and the last stages (i.e., completion time of the job in position i). Eq. (12) calculates the completion time of the job in the last sequence (i.e., makespan). Eqs. (17) and (18) show that a job in the first sequence has no blocking time and job in position i has no blocking time at the third stage, respectively. Eq. (20) indicates w j takes value only between 0 and 1. Eq. (21) shows that x ij can only take 0 or 1 value.
Meta-heuristic Method
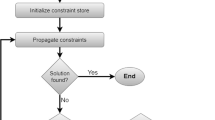
From [3], we know (AF (m, 1, 1)//) is an NP-hard problem, so by adding sequence-dependent setup time and blocking times to this model it is strongly NP-hard too. Because of this to solve the problem, we propose a meta-heuristic algorithm, namely simulated annealing (SA). This algorithm was originally proposed by Metropolis et al. [30] to simulate the annealing process. This algorithm starts with a high temperature. After generating an initial solution, it attempts to move from the current solution to one of its neighborhood solutions. The changes in the objective function values ΔE are computed. If the new solution results in a better objective value, it is accepted. However, if the new solution yields the worse value, it can be accepted according to the probability function considering the Boltzmann’s constant and the initial (or current) temperature. By accepting worse solutions, SA can avoid being trapped on local optima. It repeats this process L times at each temperature to reach the thermal equilibrium, where L is a control parameter, called the Markov chain length. The temperature T is gradually decreased by a cooling function as SA proceeds until the stopping condition is met.
Setting the parameters for the proposed SA algorithm is essential in achieving a good performance. An initial estimation for the best value of a given parameter is obtained by changing the values of that parameter while keeping all other parameters as constant. We use the following values as initial estimates of the parameters; (initial temperature T1 = 0.5, 0.1, and 0.01), (cooling factor = 0.99, 0.98, 0.97, 0.96, and 0.95), and (final temperature = 0.1, 0.125, 0.15, 0.175). Once these initial values are determined, then, the method of factorial experimental design (three values for each parameter including the initial best value of that parameter, one value above and one value below that value) is used to fine tune the values of the parameters. After these experimentations, the parameters for the SA algorithm are set as follows. The initial temperature, cooling factor, final temperature and number of iterations per fixed temperature are set to 0.1, 0.98, 0.001, and 50, respectively. Following is a general steps of the SA procedure.
Initialization
Set cooling schedule
Define neighborhood solution
Generate initial solution (s0)
Evaluate the initial solution and set s* = s0
Generate a new neighborhood solution (s0)
Set s* = s0 if f (s0) < f (s*) or set s* = s0 if p > r
Stop the algorithm if the stopping criteria is met.
Computational Results
To compare the related results, a number of test problems are solved by the use of SA and Lingo. Although GAMS and CPLEX are useful to solve the mixed-integer model, we solve a small case of this problem and the same solutions are obtained. Therefore because of our experience and knowledge, we solve all cases with Lingo 8, which is well-known optimization software using a branch-and-bound algorithm. The proposed SA is implemented in Delphi 10. The computer used in this research is a Laptop with Core 2Duo CPU processors of 1.5 GHz running under the Windows 7 operating system with 2 GB of RAM. To measure the efficiency of the proposed SA, we compare its performance against Lingo. In this paper, the processing times of the first and third stages are integer values that are randomly generated from the uniform distribution (1,100) on all m first stage machines and single third stage machine, second stage processing times are integers that are randomly generated from the uniform distribution (1, 10) on single second stage machine [3]. Setup times are integers and randomly generated from uniform distribution (1, 20) on all m machines [31]. The problem data are generated for different numbers of jobs, say 6, 7, 8, 9, 20, 40, 60, and 80. The experimentation is conducted for the number of machines at the first stage being 2, 4, 6 or 8. We choose the values of the weight α to be 0, 0.3, 0.7 or 1.
The weight values of more than 0.5 give a more weight to the weighted mean completion time criterion, whereas the values of less than 0.5 give a more weight to the C max criterion. The obtained results are shown in Tables 1 and 2. Some of the problems cannot be solved in reasonable time using Lingo. As shown in Table 2, because of an overmuch number of variables and constraints, it shows SA better time of solution than Lingo. In Figure 1, we show the average CPU time for the SA algorithm for jobs 6, 7, 8, 9, 20, 40, 60 and 80. It indicates that SA has reasonable computational time to obtain the objective function value (OFV).
Conclusions
In this paper, we have investigated a new 3-stage assembly flow shop scheduling problem with sequence-dependent setup time with blocking time that minimizes the weighted mean completion time and makespan. We have also proposed a new mathematical model solved by the proposed simulated annealing (SA) algorithm and Lingo 8. The obtained results have shown that our proposed SA was able to solve a number of test problems in a more reasonable time in comparison with Lingo. For future research, the case can be considered with machine breakdown, fuzzy data input. Also some other meta-heuristics methods can be used for soling the model.
References
Ng CT, Wang JB, Cheng TCE, Liu LL: A branch-and-bound algorithm for solving a two-machine flow shop problem with deteriorating jobs. Comput Oper Res 2010,37(1):83–90. 10.1016/j.cor.2009.03.019
Allahverdi A, Al-Anzi FS: The two-stage assembly flowshop scheduling problem with bicriteria of makespan and mean completion time. Int J Adv Manuf Technol 2007,37(1):166–177.
Koulamas S, Kyparisis G: The three-stage assembly flowshop scheduling problem. Comput Oper Res 2001,28(7):689–704. 10.1016/S0305-0548(00)00004-6
Al-Anzi FS, Allahverdi A: Heuristics for a two-stage assembly flowshop with bicriteria of maximum lateness and makespan. Comput Oper Res 2009,36(9):2682–2689. 10.1016/j.cor.2008.11.018
Hatami S, Ebrahimnejad S, Tavakkoli-Moghaddam R, Maboudian Y: Two meta-heuristics for three-stage assembly flowshop scheduling with sequence-dependent setup times. Int J Adv Manuf Technol 2010, 50: 1153–1164. 10.1007/s00170-010-2579-5
Tavakkoli-Moghaddam R, Safaei N, Sassani F: A memetic algorithm for the flexible flow line scheduling problem with processor blocking. Comput Oper Res 2009,36(2):402–414. 10.1016/j.cor.2007.10.011
Hall NG, Sriskandarajah C: A survey of machine scheduling problems with blocking and no wait in process. Oper Res 1996,44(3):510–525. 10.1287/opre.44.3.510
Yokoyama M, Santos DL: Three-stage flow-shop scheduling with assembly operations to minimize the weighted sum of product completion times. Eur J Oper Res 2005,161(3):754–770. 10.1016/j.ejor.2003.09.016
Allahverdi A, Al-Anzi FS: The two-stage assembly scheduling problem to minimize total completion time with setup times. Comput Oper Res 2009,36(10):2740–2747. 10.1016/j.cor.2008.12.001
Lee CY, Cheng TCE, Lin BMT: Minimizing the makespan in the 3-machine assembly type flowshop scheduling problem. Manag Sci 1993,39(5):616–625. 10.1287/mnsc.39.5.616
Cheng TCE, Lin BMT, Tian Y: Scheduling of a two-stage differentiation flowshop to minimize weighted sum of machine completion times. Comput Oper Res 2009,36(11):3031–3040. 10.1016/j.cor.2009.02.001
Ruiz R, Allaherdi A: Minimizing the bicriteria of makespan and maximum tardiness with an upper bound on maximum tardiness. Comput Oper Res 2009,36(4):1268–1283. 10.1016/j.cor.2007.12.013
Sun X, Morizawa K, Nagasawa H: Powerful heuristics to minimize makespan in fixed, 3-machine, assembly-type flowshop scheduling. Eur J Oper Res 2003,146(3):498–516. 10.1016/S0377-2217(02)00245-X
Qian B, Wang L, Huang DX, Wang W, Wang X: An effective hybrid DE-based algorithm for multi-objective flow shop scheduling with limited buffers. Comput Oper Res 2009,36(1):209–233. 10.1016/j.cor.2007.08.007
Liu B, Wang L, Jin YH: An effective hybrid PSO-based algorithm for flow shop scheduling with limited buffers. Comput Oper Res 2008,35(9):2791–2806. 10.1016/j.cor.2006.12.013
Wang L, Zhang L, Zheng DZ: An effective hybrid genetic algorithm for flow shop scheduling with limited buffers. Comput Oper Res 2006,33(10):2960–2971. 10.1016/j.cor.2005.02.028
Grabowski J, Pempera J: The permutation flowshop problem with blocking .A tabu search approach. Omega 2007,35(3):302–311. 10.1016/j.omega.2005.07.004
Ronconi DP: A note on constructive heuristics for the flowshop problem with blocking. Int J Prod Econ 2004,87(1):39–48. 10.1016/S0925-5273(03)00065-3
Sawik T: Mixed integer programming for scheduling flexible flow lines with limited intermediate buffers. Math Comput Model 2000,31(13):39–52. 10.1016/S0895-7177(00)00110-2
Norman AB: scheduling flowshops with finite buffers and sequence-dependent setup times. Comput Ind Eng 1999,36(1):163–177. 10.1016/S0360-8352(99)00007-8
Ronconi DP, Henriques LRS: Some heuristic algorithms for total tardiness minimization in a flowshop with blocking. Omega 2009,37(2):272–281. 10.1016/j.omega.2007.01.003
Tozkapan A, Kirca O, Chung CS: A branch and bound algorithm to minimize the total weighted flowtime for the two-stage assembly scheduling problem. Comput Oper Res 2003,30(2):309–320. 10.1016/S0305-0548(01)00098-3
Yagmahan B, Yenisey MM: A multi-objective ant colony system algorithm for flow shop scheduling problem. Expert Syst Appl 2010,37(2):1361–1368. 10.1016/j.eswa.2009.06.105
Sung CS, Kim HK: A two-stage multiple-machine assembly scheduling problem for minimizing sum of completion times. Int J Prod Econ 2008,113(2):1038–1048. 10.1016/j.ijpe.2007.12.007
Yokoyama Y: Flow-shop scheduling with setup and assembly operations. Eur J Oper Res 2008,161(3):754–770.
Liu SQ, Kozan E: scheduling a flow shop with combined buffer conditions. Int J Prod Econ 2009,117(2):371–380. 10.1016/j.ijpe.2008.11.007
Lee WC, Shiuan YR, Chen SK, Wu CC: A two-machine flowshop scheduling problem with deteriorating jobs and blocking. Int J Prod Econ 2010,124(1):188–197. 10.1016/j.ijpe.2009.11.001
Gong H, Tang L, Duin CW: A two-stage flow shop scheduling problem on a batching machine and a discrete machine with blocking and shared setup times. Comput Oper Res 2010,37(5):960–969. 10.1016/j.cor.2009.08.001
Wang L, Pan QK, Suganthan PN, Wang WH, Wang YM: A novel hybrid discrete differential evolution algorithm for blocking flow shop scheduling problems. Comput Oper Res 2010,37(3):509–520. 10.1016/j.cor.2008.12.004
Metropolis N, Rosenbluth AW, Teller AH: Equation of state calculations by fast computing machines. J Chem Phys 1953, 1087–1092.
Lin SW, Ying KC, Lee ZJ: Meta-heuristics for scheduling a non-permutation flow line manufacturing cell with sequence dependent family setup times. Comput Oper Res 2009,36(4):1110–1121. 10.1016/j.cor.2007.12.010
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author(s) declare that they have no competing interests.
Authors’ contributions
AMD surveyed the literature review and presented the model. He also drafted the manuscript. MM was responsible for revising and improving the quality of the manuscript. RTM participated in the design of problem solving approach. IS analyzed the data and the prepared the figures and tables. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Maleki-Darounkolaei, A., Modiri, M., Tavakkoli-Moghaddam, R. et al. A three-stage assembly flow shop scheduling problem with blocking and sequence-dependent set up times. J Ind Eng Int 8, 26 (2012). https://doi.org/10.1186/2251-712X-8-26
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2251-712X-8-26