Mixture probability distribution functions to model wind speed distributions

Abstract

Accurate wind speed modeling is critical in estimating wind energy potential for harnessing wind power effectively. The quality of wind speed assessment depends on the capability of chosen probability density function (PDF) to describe the measured wind speed frequency distribution. The objective of this study is to describe (model) wind speed characteristics using three mixture probability density functions Weibull-extreme value distribution (GEV), Weibull-lognormal, and GEV-lognormal which were not tried before. Statistical parameters such as maximum error in the Kolmogorov-Smirnov test, root mean square error, Chi-square error, coefficient of determination, and power density error are considered as judgment criteria to assess the fitness of the probability density functions. Results indicate that Weibull-GEV PDF is able to describe unimodal as well as bimodal wind distributions accurately whereas GEV-lognormal PDF is able to describe familiar bell-shaped unimodal distribution well. Results show that mixture probability functions are better alternatives to conventional Weibull, two-component mixture Weibull, gamma, and lognormal PDFs to describe wind speed characteristics.

Background

Growing global population along with fast depleting reserves of fossil fuels is influencing researchers to search for clean and pollution-free sources of energy such as solar, wind, and bioenergies. Wind energy is a never ending natural resource which has shown its great potential in combating climate change while ensuring clean and efficient energy. Further, rapid advances in wind turbine technology led to significant growth of wind power generation across the world. However, wind energy is more sensitive to variations with topography and wind patterns compared to solar energy. Wind energy can be harvested economically if the turbines are installed in a windy area and suitable turbine is properly selected. Wind speed forecasting is a critical factor in assessing wind energy potential and performance of wind energy conversion systems. Several probability density functions (PDFs) have been used in literature to describe wind speed characteristics which include Weibull, Rayleigh, bimodal Weibull, lognormal, gamma, etc.

Islam et al. [1] used two-parameter Weibull distribution function for wind speed forecasting and assessed wind energy potentiality at Kudat and Labuan, Malaysia. Celik [2] used Weibull-representative wind data instead of the measured data in time-series format for estimating the wind energy and had shown that estimated wind energy is highly accurately. Celik [3] made statistical analysis of wind data at southern region of Turkey and summarized that Weibull model was better than Rayleigh model in fitting the measured data distributions. Akdag et al. [4] discussed the suitability of two-parameter Weibull wind speed distribution and the two-component mixture Weibull distribution (WW-PDF) to estimate wind speed characteristics. Carta et al. [5] used WW-PDF because it is able to represent heterogeneous wind regimes in which there was evidence of bimodality or bitangentiality or, simply, unimodality. Maximum likelihood and least-square methods were used to estimate WW-PDF parameters. In [6], wind speed distributions were shown to be satisfactorily described with a log-normal function, and in [7], Weibull and lognormal distribution functions were used to fit wind speed distributions. Kiss and Imre [8] used Rayleigh, Weibull, and gamma distributions to model wind speeds both over land and sea. They found that generalized gamma distribution, which has independent shape parameters for both tails, provides an adequate and unified description almost everywhere. Generalized extreme value (GEV) distribution that combines the Gumbel, Frechet, and Weibull extreme value distributions were used to model extreme wind speeds [9–12]. In recent past, mixture distributions were used to estimate wind energy potential that are quite accurate in describing wind speed characteristics. Jaramillo and Borja [13] used mixture Weibull distribution (WW) to model bimodal wind speed frequency distribution. Akpinar et al. [14] used mixture normal and Weibull distribution (NW), which is a mixture of truncated normal distribution, and conventional Weibull distribution to model wind speeds. Tian Pau [15] employed mixture gamma and Weibull distribution (GW) which is a combination of gamma and Weibull distributions, and also mixture normal distribution (NN) which is a mixture function of two-component truncated normal distribution for wind speed modeling.

The objective of this study is to propose three new mixture distributions, viz., Weibull-lognormal (WL), GEV-lognormal (GEVL), and Weibull-GEV (WGEV) for wind speed forecasting. Comparison of the proposed mixture distributions with existing distribution functions is done to demonstrate their suitability in describing wind speed characteristics.

The rest of this paper is organized as follows: wind distribution models and goodness of fit tests used in this paper are presented in the section ‘Methods’. Results derived from this study are discussed in ‘Results and discussions’ section. Details about the data used for the analysis are given in this section. Conclusions are presented in the ‘Conclusions’ section.

Methods

Significance

The most suitable wind turbine model which needs to be installed in a wind farm is selected by careful wind energy resource evaluation. Accurate evaluation could be done using best fit distribution model. Using inappropriate distribution models results in inaccurate estimation of wind turbine capacity factor and annual energy production which in turn leads to improper estimation of levelized production cost [13]. Hence, it is important to choose an accurate distribution model which closely mimics the wind speed distribution at a particular site.

Wind distribution models

Wind distribution modeling requires analysis of wind data over a number of years. To reduce the expenses and time required to process long-term wind speed data, it is desirable to use statistical distribution functions for describing the wind speed variations. The primary tools to describe wind speed characteristics are probability density functions. The parameters of probability distribution functions which describe wind-speed frequency distribution are estimated using statistical data of a few years. Many PDFs have been proposed in recent past, but in present study Weibull, Lognormal, gamma, GEV, WW-PDF, mixture gamma and Weibull distribution, mixture normal distribution, mixture normal and Weibull distribution, and three new mixture distributions, viz., Weibull-lognormal, GEV-lognormal, and Weibull-GEV are used to describe wind speed characteristics. Parameters defining each distribution function are calculated using maximum likelihood method.

Weibull distribution

The Weibull function is commonly used for fitting measured wind speed probability distribution. Weibull distribution with two parameters is given by [1]:

Weibull PDF

$$f\left(v,k,c\right)=\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\mathit{\text{exp}}\left[-{\left(\frac{v}{c}\right)}^k\right]$$

(1)

Weibull cumulative distribution function (CDF):

$$F\left(v,k,c\right)=1-\mathit{\text{exp}}\left[-{\left(\frac{v}{c}\right)}^k\right]$$

(2)

Weibull shape and scale parameters are calculated using the maximum likelihood method [16] which is given by:

$$k={\left[\frac{{\displaystyle {\sum }_{i=1}^n{v}_i^{k}1\text{n}\left(vi\right)}}{{\displaystyle {\sum }_{i=1}^n{v}_i^k}},-,\frac{{\displaystyle {\sum }_{i=1}^{n}1\text{n}\left(vi\right)}}{n}\right]}^{-1}$$

(3)

where v _i is the wind speed in time step i and n is the number of data points. To evaluate (3) an iterative technique is used. Scale parameter is obtained by

$$c={\left[\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{v}_i^k}\right]}^{1/\text{k}}$$

(4)

Generalized extreme value distribution

GEV distribution is a flexible model that combines the Gumbel, Frechet and Weibull maximum extreme value distributions [11, 17]. GEV PDF is given by

$$\begin{array}{c}e\left(v,\zeta ,\delta ,1\right)=\left(\frac{1}{\mathrm{\delta }}\right){\left(1+\frac{\zeta \left(v-1\right)}{\delta }\right)}^{-\frac{1}{\zeta }-1}\hfill \\ \mathit{\text{exp}}{\left[-\left(1+\frac{\zeta \left(v-l\right)}{\delta }\right)\right]}^{\frac{1}{\zeta }}if\zeta \ne 0\hfill \end{array}$$

(5)

GEV CDF [17] is given by

$$E\left(v,\zeta ,\delta ,l\right)=\mathit{\text{exp}}{\left[-\left(1+\frac{\zeta \left(v-1\right)}{\delta }\right)\right]}^{\frac{-1}{\zeta }}\text{if}\zeta \ne 0$$

(6)

GEV parameters are calculated using the maximum likelihood method which maximizes the Logarithm of likelihood function given by

$$LL=1\text{n}{\prod }_{i=1}^n\left\{e\left(v_i;\zeta ,\delta ,l\right)\right\}={\Sigma }_{i=1In}^n\left\{e\left(v_i;\zeta ,1\right)\right\}$$

(7)

Lognormal distribution

Lognormal distribution is probability distribution of a random variable whose logarithm is normally distributed.

Lognormal PDF is given by [18, 19]

$$ln\left(v,Ø,\lambda \right)=\frac{1}{vØ\sqrt{2\pi }}\mathit{\text{exp}}\left[\frac{-\left(1\text{n}\left(v\right)-{\lambda }^2\right)}{2{Ø}^2}\right]$$

(8)

Lognormal CDF is written as [18]

$$LN\left(v,Ø,\lambda \right)=\frac{1}{2}+\frac{1}{2}\mathit{\text{erf}}\left[\frac{1\text{n}\left(v\right)-\lambda }{Ø\sqrt{2}}\right]$$

where

$$\mathit{\text{erf}}\left(v\right)=\frac{2}{\sqrt{\pi }}{\int }_0^v\mathit{\text{exp}}\left(-t^2\right)\mathit{dt}$$

(9)

Lognormal parameters λ and Φ estimated using maximum likelihood method which do not need an iterative procedure are given by [20]

$$\lambda =\frac{1}{N}{\displaystyle {\sum }_{i=1}^{N}1\text{n}\left(vi\right);}{Ø}^2=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{\left[1\text{n}\left(vi\right)-\lambda \right]}^2}$$

(10)

Gamma distribution

The probability density function of gamma distribution is expressed using the below function [15]

$$\text{g}\left(v,\alpha ,\beta \right)=\frac{v^{\alpha -1}}{{\beta }^{\alpha }\Gamma \left(\alpha \right)}\mathit{\text{exp}}\left[-\frac{v}{\beta }\right]$$

(11)

The cumulative Gamma distribution function is given by [20]

$$G\left(v,\alpha ,\beta \right)=\int \frac{v^{\alpha -1}}{{\beta }^{\alpha }\text{Γ}\left(\alpha \right)}\mathit{\text{exp}}\left[-\frac{v}{\beta }\right]dv$$

(12)

Gamma distribution parameters are estimated using maximum likelihood method that maximizes the logarithm of likelihood function which is given by:

$$LL=1\text{n}{\prod }_{i-1}^n\left\{h\left(v_i;\alpha ,\beta \right)\right\}={\displaystyle {\sum }_{i-1}^{n}1\text{n}\left\{h\left(v_i;\alpha ,\beta \right)\right\}}$$

(13)

Two-component mixture Weibull distribution

The probability density function, which depends on five parameters (v; k₁, c₁, k₂, c₂, w) is given by [5]

$$\begin{array}{c}ff\left(v;k_1,c_1,k_2,c_2,w\right)=wf\left(v;k_1,c_1\right)\hfill \\ +\left(1-w\right)f\left(v;k_2,c_2\right)\hfill \end{array}$$

(14)

The cumulative distribution function is given by [5]

$$\begin{array}{c}FF\left(v;k_1,c_1,k_2,c_2,w\right)=wF\left(v;k_1,c_1\right)\hfill \\ +\left(1-w\right)F\left(v;k_2,c_2\right)\hfill \end{array}$$

(15)

Relevant likelihood function is

$$LL={\displaystyle {\sum }_{i=1}^{n}1\text{n}\left\{wf\left(v;k_1,c_1\right)+\left(1-w\right)f\left(v;k_2,c_2\right)\right\}}$$

(16)

Mixture gamma and Weibull distribution

The probability density function and cumulative distribution function of the mixture gamma and Weibull distribution are given by [15]

$$\begin{array}{c}h\left(v;\alpha ,\beta ,k,c,w\right)=wg\left(v;\alpha ,\beta \right)\hfill \\ +\left(1-w\right)f\left(v;k,c\right)\hfill \end{array}$$

(17)

$$\begin{array}{c}H\left(v;\alpha ,\beta ,k,c,w\right)=wG\left(v;\alpha ,\beta \right)\hfill \\ +\left(1-w\right)F\left(v;k,c\right)\hfill \end{array}$$

(18)

Relevant likelihood function is

$$LL={\displaystyle {\sum }_{i-1}^{n}1\text{n}\left\{wg\left(v;\alpha ,\beta \right)+\left(1-w\right)f\left(v;k,c\right)\right\}}$$

(19)

Mixture normal distribution

The probability density function of singly truncated normal distribution is given by [15]

$$q\left(v;\mu ,\sigma \right)=\frac{1}{I\left(\mu ,\sigma \right)\sigma \sqrt{2\pi }}\mathit{\text{exp}}\left[-\frac{v-{\mu }^2}{2{\sigma }^2}\right]\mathit{for}v\ge 0\text{,}$$

(20)

where I(μ,σ) is the normalization factor that leads the integration of the truncated distribution to one is expressed as

$$I\left(\mu ,\sigma \right)\frac{1}{\sigma \sqrt{2\pi }}{\int }_0^{\infty }\mathit{\text{exp}}\left[-\frac{{\left(v-\mu \right)}^2}{2{\sigma }^2}\right]dv\text{.}$$

(21)

The cumulative truncated normal distribution is given by

$$Q\left(v;\mu ,\sigma \right)={\displaystyle {\int }_0^v}\frac{1}{I\left(\mu ,\sigma \right)\sigma \sqrt{2\pi }}\mathit{\text{exp}}\left[-\frac{v-{\mu }^2}{2{\sigma }^2}\right]dv$$

(22)

The mixture function of two component truncated normal distribution from the above can be written as [15]

$$\begin{array}{c}r\left(v;{\mu }_1{\sigma }_1,{\mu }_2,{\sigma }_{2}w\right)=wq\left(v;{\mu }_1{\sigma }_1\right)\hfill \\ +\left(1-w\right)q\left(v;{\mu }_2{\sigma }_2\right)\hfill \end{array}$$

(23)

The cumulative distribution function is given by

$$\begin{array}{c}R\left(v;{\mu }_1{\sigma }_1,{\mu }_2,{\sigma }_{2}w\right)=wQ\left(v;{\mu }_1{\sigma }_1\right)\hfill \\ +\left(1-w\right)Q\left(v;{\mu }_2{\sigma }_2\right)\hfill \end{array}$$

(24)

Relevant likelihood function to estimate the five parameters is

$$LL={\displaystyle {\sum }_{i=1}^{n}1\text{n}}\left\{wq\left(v;{\mu }_1{\sigma }_1\right)+\left(1-w\right)q\left(v;{\mu }_2{\sigma }_2\right)\right\}$$

(25)

Mixture normal and Weibull distribution

The probability density function of the mixture distribution comprising of truncated normal and conventional Weibull is written as [15]

$$s\left(v;\mu ,\sigma ,k,c\right)=wq\left(v;\mu ,\sigma \right)+\left(1-w\right)f\left(v;k,c\right)$$

(26)

Its cumulative distribution function is given as

$$S\left(v;\mu ,\sigma ,k,c\right)=wQ\left(v;\mu ,\sigma \right)+\left(1-w\right)F\left(v;k,c\right)$$

(27)

Relevant likelihood function to estimate the five parameters is

$$LL={\displaystyle {\sum }_{i=1}^{n}1\text{n}}\left\{wq\left(v;\mu ,\sigma \right)+\left(1-w\right)f\left(v;k,c\right)\right\}$$

(28)

Mixture Weibull and GEV distribution

The probability density function of the mixture distribution comprising Weibull and GEV functions which is applied for the first time to model wind speed distribution is written as

$$\begin{array}{c}t\left(v;k,c,\zeta ,\delta ,l\right)=wf\left(v;k,c\right)\hfill \\ +\left(1-w\right)e\left(v;\zeta ,\delta ,l\right)\hfill \end{array}$$

(29)

Its cumulative distribution function is given as

$$\begin{array}{c}T\left(v;k,c,\zeta ,\delta ,l\right)=wF\left(v;k,c\right)\hfill \\ +\left(1-w\right)E\left(v;k,c,\zeta ,\delta ,l\right)\hfill \end{array}$$

(30)

Relevant likelihood function to estimate the six parameters is

$$LL={\displaystyle {\sum }_{i=1}^{n}1\text{n}}\left\{wf\left(v;k,c\right)+\left(1-w\right)e\left(v;\zeta ,\delta ,l\right)\right\}$$

(31)

Mixture Weibull and lognormal distribution

The probability density function of the mixture distribution comprising Weilbull and lognormal of functions which is applied for the first time to model wind speed distribution is written as

$$u\left(v;k,c,\lambda ,\phi \right)=wf\left(v;k,c\right)+\left(1-w\right)l\left(v;\lambda ,\phi \right)$$

(32)

Its cumulative distribution function is given as

$$\begin{array}{c}U\left(v;k,c,\lambda ,\phi \right)=wF\left(v;k,c\right)\hfill \\ +\left(1-w\right)L\left(v;\lambda ,\phi \right)\hfill \end{array}$$

(33)

Relevant likelihood function to estimate the five parameters is

$$LL={\displaystyle {\sum }_{i=1}^{n}1\text{n}}\left\{wf\left(v;k,c\right)+\left(1-w\right)L\left(v;\lambda ,\phi \right)\right\}$$

(34)

Mixture GEV and lognormal distribution

The probability density function of the mixture distribution comprising GEV and lognormal functions which is applied for the first time to model wind speed distribution is written as

$$\begin{array}{c}v\left(v;\zeta ,\delta ,l,\lambda ,\phi \right)=we\left(v;\zeta ,\delta ,l\right)\hfill \\ +\left(1-w\right)l\left(v;\lambda ,\phi \right)\end{array}$$

(35)

Its cumulative distribution function is given as

$$\begin{array}{c}V\left(v;\zeta ,\delta ,l,\lambda ,\phi \right)=wE\left(v;\zeta ,\delta ,l\right)\hfill \\ +\left(1-w\right)L\left(v;\lambda ,\phi \right)\hfill \end{array}$$

(36)

Relevant likelihood function to estimate the five parameters is

$$LL={\displaystyle {\sum }_{i=1}^{n}1\text{n}}\left\{we\left(v;\zeta ,\delta ,l\right)+\left(1-w\right)l\left(v;\lambda ,\phi \right)\right\}$$

(37)

Goodness-of-fit tests

Goodness-of-fit tests are used to measure the deviation between the predicted data using theoretical probability function and the observed data. In this paper five statistical errors are considered as judgment criteria to evaluate the fitness of PDFs.

Kolmogorov-Smirnov test

The first one is the Kolmogorov-Smirnov test (K-S), which is defined as the maximum error in cumulative distribution functions [21].

$$\mathit{K-S}=\mathit{\text{max}}\left|C\left(v\right)-0\left(v\right)\right|$$

(38)

where C(v) and O(v) are the cumulative distribution functions for wind speed not exceeding v calculated by distribution function and observed wind speed data respectively. Lesser K-S value indicates better fitness of the PDF.

R² test

R² test is used widely for goodness-of-fit comparisons and hypothesis testing because it quantifies the correlation between the observed cumulative probabilities and the predicted cumulative probabilities of a wind speed distribution. A larger value of R² indicates a better fit of the model cumulative probabilities $\widehat{F}$ to the observed cumulative probabilities F. R² is defined as [22]:

$$R^2=\frac{{\displaystyle {\sum }_{i=1}^n{\left({\widehat{F}}_i-\overline{F}\right)}^2}}{{\displaystyle {\sum }_{i=1}^n{\left({\widehat{F}}_i-\overline{F}\right)}^2}+{\displaystyle {\sum }_{i=1}^n{\left(F_i-{\widehat{F}}_i\right)}^2}}$$

(39)

where $\overline{F}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\widehat{F}}_i}$ The estimated cumulative probabilities $\widehat{F}$ are obtained from cumulative distribution functions (CDFs).

Chi-square error

Chi-square error is used to assess whether the observed probability differs from the predicted probability. Chi-square error is given by

$$x^2={\displaystyle {\sum }_{i=1}^n\frac{{\left(F_i-{\widehat{F}}_i\right)}^2}{{\widehat{F}}_i}}$$

(40)

Root mean squared error

Root mean squared error (RMSE) provides a term-by-term comparison of the actual deviation between observed probabilities anead predicted probabilities. A lower value of RMSE indicates a better distribution function model.

$$\text{RMSE}={\left[\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\left(F_i-{\widehat{F}}_i\right)}^2}\right]}^{1/2}$$

(41)

Power density error (PDE)

The relative error between the wind power density calculated from actual time-series data and that from theoretical probability function is expressed as [23]

$$\text{PDE}=\left(\frac{P{D}_{\mathit{tp}}-P{D}_{\mathit{ts}}}{P{D}_{\mathit{ts}}}\right)\ast 100$$

(42)

where PD _ts is the wind power density calculated from actual time-series data which is given by

$$P{D}_{\mathit{ts}}=\frac{1}{2}\rho \overline{v^3}$$

(43)

where PD _tp is the wind power density based on a theoretical probability density function fn(v) which is given by

$$P{D}_{\mathit{tp}}=\frac{1}{2}\rho \int v^{3}fn\left(v\right)dv$$

(44)

Results and discussion

Wind speed data from four wind stations were used in evaluating different PDFs to assess their suitability. Wind speed data provided by National Data Buoy Center [24] at five stations 42056 (Yucatan Basin), 46012 (Half Moon Bay, 24NM South Southwest of San Francisco, CA), 46014 (PT Arena, 19NM North of Point Arena, CA), and 46054 (Santa Barbara W 38 NM West of Santa Barbara, CA) are used for wind speed analysis. Ten-minute mean wind speed data recorded at 5 m above the sea level are used for present studies.

Wind data of over the period 2008 to 2010 is used for wind station 42056.

For station 46012, wind data over a period of 10 years (2001 to 2010) is used for statistical analysis.

Wind data of station 46014 over a period of three years (2008 to 2010) is analyzed for wind distribution modeling.

For wind station 46054 data over the period (1999 to 2000) is used for statistical analysis.

In the present study, suitability of the PDFs is assessed using goodness-of-fit tests. All computational procedures are carried out in MATLAB software package. Computed parameter values of different PDFs used for all the four stations are presented in Table 1.

Table 1 Computed parameter values of different probability density functions

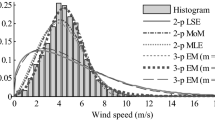
The mean and standard deviation of observed wind speed for Station 42056 are 6.91888 m/s and 2.56768 m/s, respectively. Wind frequency histogram resembles familiar bell-shaped curve; hence, Weibull PDF fits the observed distribution well. The statistical parameters for fitness evaluation of PDFs currently analyzed are presented in Table 2. All the PDFs except lognormal, GEV, and gamma are able to describe the wind speed characteristics well which is evident from their small power density errors shown in Table 2. Considering K-S error, χ² error, RMSE and PDE, the distribution functions lognormal, GEV and Gamma have large errors indicating their inadequacy in modeling wind speeds. Results presented in Table 2 show clearly that proposed mixture GEVL PDF provided the best fit of observed wind speed distribution. From Figure 1, it is evident that GEVL distribution provides a close fit throughout the entire wind speed spectrum when compared to other distributions. The higher value of R² and the lower values of K-S error, RMSE and chi-square error indicate that proposed GEVL distribution is more accurate than other PDFs in modeling wind speeds of Station 42056.

Table 2 Statistical errors for different distribution functions of Station 42056

Figure 1

Predicted and observed wind frequencies of Station 42056.

Station 46012 has a mean and standard deviation of 5.59185 m/s and 3.13391 m/s, respectively, for the observed wind speed. Statistical errors, K-S, R², χ², and RMSE given in Table 3 indicate that proposed mixture WGEV distribution provides best fit for the observed wind frequency distribution, which is closely followed by GW, WL, GEVL, and WW mixture distributions. Convention PDFs such as lognormal and gamma, over predicted wind speeds which are in the range of 2 to 5 m/s and 13 to 24 m/s, respectively. These PDFs have under predicted speeds between 5 to 11 m/s. Apart from WGEV and WL, other mixture PDFs and conventional PDFs over predicted wind speeds in the range of 3 to 5 m/s which are reflected by the overestimated predicted probabilities as depicted in Figure 2. Results indicate that mixture PDFs perform better compared to conventional single PDFs.

Table 3 Statistical errors for different distribution functions of Station 46012

Figure 2

Predicted and observed wind frequencies of Station 46012.

Mean and standard deviation of wind speed for Station 46014 are 6.19907 m/s and 3.71888 m/s, respectively. From Figure 3, it is seen that WGEV, WG, WW, and WN distributions are able to model wind speed characteristics better than other PDFs. All other distributions have either over- or under-predicted wind speeds apart from these three. Results presented in Table 4 clearly show that, considering K-S error, χ², and RMSE, GW PDF has the smallest error followed by WGEV, WW, and NW. If R² error is considered, GW has a value very close to 1.0, confirming its superiority in performance followed by WGEV, WW, and NW distributions.

Figure 3

Predicted and observed wind frequencies of Station 46014.

Table 4 Statistical errors for different distribution functions of Station 46014

Wind regime of Station 46054 has bimodal distribution with mean and standard deviation of 8.1261 m/s and 4.2390 m/s, respectively. Compared to conventional single PDFs, mixture PDFs have performed well in modeling the wind speeds. Lognormal, gamma, Weibull, and GEV fared poorly in describing the wind characteristics compared to other mixture PDFs. As seen from Figure 4 and statistical parameters from Table 5, two component mixture Weibull distribution (WW) provided the best fit for the observed wind data, closely followed by proposed mixture function WGEV.

Figure 4

Predicted and observed wind frequencies of Station 46054.

Table 5 Statistical errors for different distribution functions of Station 46054

Figures 1 to 4 show that mixture PDFs fit much better than the conventional Weibull, lognormal, and gamma distributions. Proposed mixture distributions GEVL for Station 42056 and WGEV for Station 46012 have outperformed other existing mixture and conventional single distributions. For Station 46054, WW distribution provided a better fit than others, while WGEV being the close second best fit.

Conclusions

In the present article, a comparison of distribution models has been undertaken for describing wind regimes of four wind stations. Common conventional PDFs and mixture PDFs along with three proposed new mixture PDFs, viz., WGEV, GEVL, and WL are used for wind speed modeling. It is shown that conventional PDFs, such as Weibull, lognormal, and gamma, are inadequate; hence, mixture functions are used to model the observed wind speed distributions better. Though the superiority of proposed mixture functions in Station 46014 is not very significant, the proposed mixture distributions GEVL for Station 42056 and WGEV for Station 46012 have provided better fit of the empirical data than other existing mixture distributions. For Station 46054, both WW and WGEV are found more suitable for describing wind speed distributions than other distributions. The performance difference between WW and WGEV distributions is not significant for this station. Results show clearly that proposed mixture PDFs, WGEV and GEVL, provide viable alternative to other mixture PDFs in describing wind regimes. Mixture PDFs which include GEV are able to provide close fit, particularly for high speed ranges of the wind spectrums. This is critical for wind speed applications as wind power is proportional to the cube of wind speed. Hence, mixture combinations of GEV with other conventional distributions need to be tried out for further analysis.

Authors' information

RK is an assistant professor in the Electrical Engineering Department, Jawaharlal Nehru Technological University, Kakinada, India. His areas of interest include distribution system planning and distributed generation. SRR is an associate professor of the same university. His areas of interest include electric power distribution systems and power systems operation and control. SVLN is a professor of Computer Science and Engineering in the School of IT, Jawaharlal Nehru Technological University, Hyderabad, India. His areas of interests include real time power system operation and control, IT applications in power utility companies, web technologies, and e-governance. KMP is a postgraduate student of the Department of Electrical and Electronics Engineering at JNTU Kakinada, India. His areas of interest include probabilistic DG planning and energy systems.