Optical properties of pure and modified poly(vinyl chloride)

Abstract

Background

In this study, poly(vinyl chloride) (PVC) is considered one of the most versatile plastics. It is the second largest manufactured resin by volume worldwide.

Results

To study the optical properties of modified PVC containing 1,3,4-thiadiazole and phthalyl groups in the repeating units, thin films of the prepared polymers (P I, P II, P III, P IV, P V, and PVC) were casted from tetrahydrofuran solvent with a thickness of 30 μm. The optical properties were studied in the range of 200 to 600 nm, and the optical data were analyzed and interpreted in terms of the theory of phonon-assisted direct electronic transitions; the measured E_g of pure and modified PVC increases in the following order:

$$\overrightarrow{\mathrm{P}\mathrm{II},\mathrm{P}\mathrm{IV},\mathrm{P}\mathrm{V},\mathrm{P}\mathrm{I},\mathrm{P}\mathrm{III},\mathrm{and}\mathrm{PVC}}\text{.}$$

Also, the refractive index was measured.

Conclusions

The results showed that for all compositions, the refractive index decreases with increasing wavelength.

Background

Modification of polymers has received greater attention as it brings specific properties to the modified material, such as enhanced thermal stability, multiphase physical responses, compatibility, impact response, flexibility, and rigidity [1]. Poly(vinyl chloride) (PVC) is one of the most versatile plastics. It is the second largest manufactured resin by volume worldwide [2].

The modification of PVC lies basically in the dechlorination process, including both substitution and elimination. Because of the peculiarities of the material relevant to its applications, the chemical functionalization of PVC seems permanent to improve and modify the polymer properties [3].

Synthesis of polymer-bound chelating ligands has been reported. A number of ligands including polydentate amines, crown ethers, phosphines, and bipyridines have been bound with mainly polystyrene divinylbenzene copolymers [4, 5].

These studies are mostly concerned with ion-binding and catalytic aspects. Very little information appears to exist as to whether, and to what extent, such organic compounds can influence the properties of the macromolecule. Recently, scientists were able to modify PVC by introducing aromatic and heterocyclic moieties through halogen displacement reaction. PVC, thus modified, showed improved overall photochemical stability and optical properties [6, 7]. In this paper, we present results of such a study on the optical properties of pure and modified PVC films.

Methods

Optical measurements

The best definition of the energy gap is the minimum energy difference between the lowest minimum of the conduction band and the highest maximum of the valance band [8]. The value and shape of the mobility gap in PVC depend on the proportion conditions such as substrate temperature, degree of impurity, and defect of the material. Any variation in such parameters leads to a shift in the absorption edge towards higher or lower energy. The absorption coefficient can be determined from the normal incidence transmission through plane-parallel plate of thickness (d), and interference and multiple reflections are neglected. The reflectance (R) and transmittance (T) are related by Equation 1:

$$T=B{\left(1-R\right)}^{2}exp\left(-\mathit{\alpha d}\right)$$

(1)

where B is a constant. This equation can be rewritten as follows:

$$\mathit{\alpha d}=2.303A+\mathrm{Ln}\left[B{\left(1-R\right)}^2\right]\text{,}$$

(2)

where A is the optical absorbance (A = −log T).

So, the absorption coefficient α(ω) in terms of absorbance becomes

$$\alpha \left(\omega \right)=2.303\left(A/d\right)\text{.}$$

(3)

For band-to-band transitions, the energy dependence of the absorption coefficient is of the form

$$\alpha ={\alpha }_0{\left(\mathit{h\nu }-E_{\mathrm{g}}\right)}^r/\mathit{h\nu }\text{,}$$

(4)

where hν is the photon energy, E_g is the energy gap, r is a constant depending on the type of electronic transitions which takes the value 1/2 for allowed direct transition and 3/2 for forbidden direct transition, and the absorption coefficient α ≥ 10⁴ cm⁻¹. The energy dependence absorption coefficient is in the form

$$\alpha ={\alpha }_0{\left(\mathit{h\nu }-E_{\mathrm{g}}\pm E_{\mathrm{p}}\right)}^r/\mathit{h\nu }\text{,}$$

(5)

where E_g is the minimum energy gap, E_p is the phonon energy, (+) represents absorbance, (−) represents emission, r takes the values 2 for allowed indirect transition and 3 for forbidden indirect transition, and the absorption coefficient α < 10⁴ cm⁻¹. By plotting (αhν)^1/r vs. hν for a fixed r value, the extrapolation of the linear part could be used to define E_g[7].

Results and discussion

The relation of (αhν)² and (αhν)^1/2 vs. photon energy for the PVC sample is shown in Figure 1 for allowed transition. For modified samples shown in Figures 2, 3, 4, 5, and 6, the shift in the energy gap could be attributed to the formation of polarons in the modified films. The evidence of polaron formation is that the reaction in the band-to-band transition is due to the shifting of the band density of state toward the energy gap. The effect of the organic addition on the values of phonon energies is also investigated, and the results are shown in Table 1.

Figure 1

Direct and indirect allowed energy gap for PVC. (a) Direct allowed energy gap for PVC (αhν)². (b) Indirect allowed energy gap for PVC (αhν)^1/2.

Figure 2

Direct and indirect allowed energy gap for P I. (a) Direct allowed energy gap for P I (αhν)². (b) Indirect allowed energy gap for P I (αhν)^1/2.

Figure 3

Direct and indirect allowed energy gap for P II. (a) Direct allowed energy gap for P II (αhν)². (b) Indirect allowed energy gap for P II (αhν)^1/2.

Figure 4

Direct and indirect allowed energy gap for P III. (a) Direct allowed energy gap for P III (αhν)². (b) Indirect allowed energy gap for P III (αhν)^1/2.

Figure 5

Direct and indirect allowed energy gap for P IV. (a) Direct allowed energy gap for P IV (αhν)². (b) Indirect allowed energy gap for P IV (αhν)^1/2.

Figure 6

Direct and indirect allowed energy gap for P V. (a) Direct allowed energy gap for P V (αhν)². (b) Indirect allowed energy gap for P V (αhν)^1/2.

Table 1 The energy band gap according to the direct allowed and indirect allowed transitions

The energy gaps were measured by adopting the data of energy gap (see Table 1 and Figures 1, 2, 3, 4, 5, and 6). The E_g for PVC in the presence of additives increases in the following order:

$$\overrightarrow{\mathrm{P}\mathrm{II},\mathrm{P}\mathrm{IV},\mathrm{P}\mathrm{V},\mathrm{P}\mathrm{I},\mathrm{P}\mathrm{III},\mathrm{and}\mathrm{PVC}}\text{.}$$

The presence of an ion pair of electrons at different atoms, such as sulfur and nitrogen, for the stereochemistry of the polymer leads to the change of the value of energy gap rather than PVC.

The tail of the absorption edge is exponential, indicating the presence of localized states in the energy band gap. The amount of tailing can be predicted to a first approximation by plotting the absorption edge data in terms of an equation originally given by Urbach. The absorption edge of nonmetallic materials gives a measure of the energy band gap, and the exponential dependence of the absorption coefficient, α, on photon energy, hν, is found to hold over several decades for a polymeric material and takes the following form:

$$\alpha ={\alpha }_0{e}^{\left(\frac{\mathit{h\nu }}{E_{\mathrm{t}}}\right)}\text{,}$$

(6)

where α₀ is a constant and E_t is interpreted as the width of the tails of localized states in the gap region. To evaluate the values of α₀ and E_t, α should be in the logarithmic scale as a function of photon energy hν as shown in Figure 2. The reciprocal of the slope of each line yields the magnitude of E_t and its values for different polymeric films. It is clear that modification increases the width of the tail of localized states and decreases the energy gap of PVC thin films. Using Equation 6 at a constant temperature, a graph representing α on the y-axis and energy E (eV) on the x-axis (Figure 7) in the range of the Urbach tail would yield a straight line.

Figure 7

Plots of α vs. E of the pure and modified PVC.

The refractive index is a suitable state parameter directly correlated to the material density. The refractive index, n(λ), was determined from the absolute values of the transmittance and reflectance of the investigated films using the following formula:

$$n=\left[\frac{1+R}{1-R}\right]+{\left[\frac{4R}{{\left(1-R\right)}^2}-k^2\right]}^{1/2}\text{,}$$

(7)

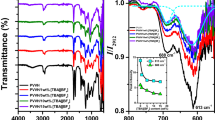
where k is the extinction coefficient and R is the optical reflectance. The extinction coefficient can be obtained from the relation where k = αλ/ 4π. Plots in Figure 8 represent the dispersion in the refractive index for pure and modified PVC thin films in the investigated range of wavelengths. Inspection of Figure 8 indicates that for all compositions, the refractive index decreases with increasing wavelength.

Figure 8

The refractive index dispersion curves of pure and modified PVC.

Table 2 illustrates the refractive index values for all polymers at a wavelength of 600 nm (for the values of other polymer wavelength, see Additional file 1).

Table 2 The refractive index of pure and modified PVC at λ = 600 nm

Experimental

All the polymers were prepared as described by [9] (Scheme 1). A solution of PVC or modified PVC (5%) in tetrahydrofuran (THF) was used to prepare the films. The polymeric films were prepared by casting the polymers (P I, P II, P III, P IV, P V, and PVC) onto leveled glass plates. The films were prepared by evaporation technique at room temperature for 24 h. To remove the possible residual THF solvent, the film samples were further dried at room temperature for 3 h under reduced pressure. The samples have the same thickness of 30 μm (measured using a micrometer type 2610 A, Mainz, Germany). The optical absorbance (A) of the samples was measured as a function of the wavelength (λ) which ranged from 200 to 600 nm using a computerized Shimadzu UV-160A UV–vis spectrophotometer (Kyoto, Japan) with a full-scale absorbance up to 2.5. The light sources are halogen lamp and socket deuterium lamp, and the detector is a Si photodiode. All measurements were performed at room temperature.

Scheme 1

Structures of polymers.

Conclusions

The study on the effect of PVC modification with 1,3,4-thiadiazole and phthalyl groups in the repeating units on its optical properties has shown that the energy gap of modified polymers decreases in comparison with that of pure PVC, and for all compositions, the refractive index decreases with increasing wavelength.