Abstract
This paper presents molecular dynamics (MD) modeling for calculating the specific heat of nanofluids containing copper nanoparticles. The Cu nanoparticles with 2-nm diameter were considered to be dispersed in water as base liquid. The MD modeling procedure presented and implemented to calculate the specific heat of nanofluids with volume fractions of 2 to 10%. Obtained results show that the specific heat capacity of Cu-water nanofluids decreases gradually with increasing volume concentration of nanoparticles. The simulation results are compared with two existing applied models for prediction of the specific heat of the nanofluid. The obtained specific heat results from the MD simulation and the prediction from the thermal equilibrium model for calculating specific heat of nanofluids exhibit good agreement and the other simple mixing model fails to predict the specific heat capacity of Cu-water nanofluids particularly at high volume fractions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Background
Nanofluids are a new class of nanotechnology-based heat transfer fluids produced by dispersing nanoparticles with sizes typically smaller than 100 nm into traditional heat transfer fluids such as water, ethylene glycol, and engine oil. Due to small sizes and very large specific surface areas of the nanoparticles, nanofluids have novel properties like high thermal conductivity, superior critical heat flux (CHF), minimal clogging in flow, and improved heat transfer coefficient [1–4]. These characteristics of nanofluids make them potentially useful in a plethora of engineering applications ranging from use in the automotive industry to the medical field to use in power plant cooling systems as well as computers [5].
In order to study the heat transfer performance of nanofluids and use them in practical applications, it is necessary first to study their thermal properties. Until now, there are numerous experimental and theoretical reports for the thermal conductivity and the viscosity of a variety of nanofluids [6–12]. The density of the nanofluids has been reported to be consistent with the mixing theory [13, 14]. However, the specific heat capacity, c p , one of the main parameters involved in calculating heat transfer rate of nanofluids, has received very little attention. This property has an important role in describing the nanofluid flow thermal status, measuring the thermal diffusivity and the spatial temperature inside the flow.
Two models have been extensively applied in the experimental and numerical nanofluid investigations; the first one is similar to the mixing theory for ideal gas mixtures. In this model, the specific heat capacity of a nanofluid is given as
where φ is the volume fraction of nanoparticles. The subscripts nf, bf, and n refer to the nanofluid, base fluid, and nanoparticles, respectively. Many researchers have used this model to calculate the specific heat capacity of nanofluids in their studies [13, 15–21].
The second model assumes that the base fluid and the nanoparticles are in thermal equilibrium. Therefore, the nanofluid specific heat capacity is expressed as
where ρ is the density.
This model has also been chosen as a base formula in many nanofluid studies [22–26]. It should be noted that the deviation between the two models is too large to be ignored, especially for high volume fractions of nanoparticles.
Zhou and Ni [27] conducted an experimental study of the specific heat capacity of water-based Al2O3 nanofluid with a differential scanning calorimeter (DSC). Their results indicated that the specific heat capacity of nanofluids decreases gradually as the nanoparticle volume fraction increases. Moreover, their results are in good agreement with the thermal equilibrium model, Equation (2), and the other simple mixing model, Equation (1), failed to predict the specific heat capacity of nanofluids. Vajjha and Das [28] measured the specific heat of three nanofluids containing aluminum oxide, zinc oxide, and silicon dioxide nanoparticles. The base fluids were ethylene glycol and water (60:40 EG/W) and deionized water. Measurements were conducted over a temperature range of 315 to 363 K. Their results were not in close agreement with the existing equations for the specific heat of nanofluids. They developed a new general correlation for the specific heat as functions of particle volumetric concentration, temperature, and the specific heat of both the particle and the base fluid from their set of experimental data.
In another study, Zhou et al. [29] reviewed briefly the definition of heat capacity and measured the specific heat capacity of nanofluids made by ethylene glycol with the inclusion of CuO nanoparticles at room temperature using the quasisteady-state principle. The comparison of their measured experimental data and the predictions of models illustrated that they are in good agreement with the thermal equilibrium model.
The purpose of our study is to investigate the specific heat capacity of nanofluids using the molecular dynamics (MD) simulation method and to compare the results with the mentioned models.
The MD is a powerful computational technique that simulates the real behavior of materials by solving the equation of motion for a system of particles [30–32]. It can predict the physical properties of materials by assuming an interacting potential between particles. Using this method, the trajectory and physical movements of atoms, molecules, and nanoparticles in the system can be determined. The atoms are allowed to interact with each other and various quantities such as pressure, temperature, energy, and so on are calculated. Moreover, it can predict the physical properties of materials by assuming a suitable potential between particles. The interactions between atoms are described by different potentials and force fields. Since there is no further essential assumption in MD, it can be used as an accurate tool to study the results obtained from other classical models with a wide range of applicability in nanotechnology, biochemistry, and biophysics fields. However, there are some limitations in MD simulations such as number of particles and simulation time due to the available computational power. During the past few years, MD has been widely employed for prediction of thermal properties of nanofluids which provided comprehensive knowledge of heat transfer mechanism at nanoscale [33–40]. In this way, most of the studies have been focused on thermal conductivity enhancement and one could not find adequate MD literature on specific heat capacities of nanofluids.
In this paper, we have modeled the Cu-water nanofluids with different volume fractions of copper nanoparticles using MD simulation and compared the specific heat capacity of nanofluids with theoretical models. The simulation details, results on specific heat capacities, and their variations with different volume fractions are explained in the following sections.
Methods
MD Simulation details
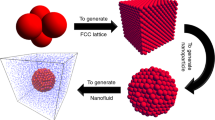
Copper nanoparticles with 2-nm diameter have been considered in water as base fluid. The equilibrium structure of a nanofluid is shown in Figure 1. The water molecules are randomly distributed around the nanoparticles. The inter-atomic interaction between nanoparticles is modeled by pair-wise Lennard-Jones (LJ) potential as
where ϵ and σ are the LJ energy and length parameters, respectively, and r is the inter-atomic distance. The LJ potential has lower computational costs compared with the other existing potentials for modeling copper. The LJ parameters, i.e., ϵ and σ, for copper are shown in Table 1. Here, water molecules are considered by the rigid TIP3P model as implemented in CHARMM which specifies a three-site rigid water molecule with charges and Lennard-Jones parameter assigned to each of the three atoms [41]. This model is very popular for MD simulations because of simplicity and computational efficiency. To compute for the long-range Coulombic interactions, we used the particle-particle-particle-mesh (pppm) method [42]. An additional switching function S(r) that ramps the energy and force smoothly to zero is used in both LJ and Columbic potentials as
where rc,in and rc,out are inner and outer cut off radii equal to 8 and 10 Å, respectively.
The water-Cu and water-water interactions are described by common Lorentz-Berthelot combination rule as
where i and j are denoted to non-bonded atoms in the system. The LJ parameters for nonbonding interactions are shown in Table 1.
The Molecular dynamics simulations are performed initially in NVE ensembles as well as the Langevin thermostat over 100 ps to relax the system. The system is then performed in NPT integration for 400 ps, using the Nose/Hoover temperature thermostat [44] and the Nose/Hoover pressure barostat [45], implemented as described in [46]. After reaching the system to T = 298.5 K and atmospheric pressure, the thermodynamics quantities are recorded every 1 fs time steps. All MD simulations were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator Package (LAMMPS) [47].
The constant-pressure specific heat is considered as c p = (∂E/∂T) p , which is usually defined in terms of energy fluctuations as
where 〈δE2〉 = 〈E2〉 − 〈E〉2[48, 49].
The energy fluctuation for a particular case (φ = 2%) is shown in Figure 2. Since, in the NPT ensemble, the temperature is artificially controlled by the thermostat, the total energy fluctuates around its mean value.
Results and discussion
Validation for pure water and copper
As the existing literature does not give any information about experimental results for the specific heat of Cu-water nanofluids, to validate our MD simulation procedure, the specific heat of pure water and pure copper at standard condition (T = 298.5 K and P = 1 atm) were calculated separately. To compute for the specific heat, we consider 1,000 molecules of water and 500 copper atoms. These values are the minimum number of particles used in all our simulations. The specific heat capacities of water and copper are computed for different total number of time steps for averaging in Equation (6). Figure 3 shows that the results are converging and 105 number of time steps for averaging is sufficient to be in good agreement with experimental values of specific heat capacities of water and copper.
Specific heat capacity for water-Cu nanofluid
After validating our method, the MD simulation results of the specific heat of nanofluid are presented here. Moreover, the obtained results by MD are compared with the mentioned theoretical models. The nanofluids with 2%, 4%, 6%, 8%, and 10% volume fractions are considered in the MD simulations. In all cases, the diameters of Cu nanoparticles are set to 2 nm. It should be noted that the Cu nanoparticles have not tethered to its initial position and can freely have its Brownian motions in our simulation.
The specific heat results are plotted in Figure 4. As shown, the c p decreases when the volume fraction is increased. As shown in Figure 3, the specific heat of Cu nanoparticles is much lower than the water base fluid. Therefore, by the increase in nanoparticle fraction, the portion of heat absorption with these lower specific heat nanoparticles is increased and lead to the decreasing in nanofluid specific heat. This reduction is consistent with the theoretical models. Moreover, the same reduction in specific heat by increasing in nanoparticle fraction has been observed in experimental studies [27].
Figure 4 illustrates that there are good agreements between MD results and thermal equilibrium model predictions, Equation (2) (black points), and the other mixing model, Equation (1) (green points), failed to predict the specific heat of nanofluids particularly for large values of nanoparticle volume fractions. However, at very small values of volume fractions, both models and MD simulation data are converging.
Moreover, the effects of the number and size of the nanoparticles have been investigated by considering two Cu nanoparticles with diameter of 1 nm. It is found that the result is very close to the case of simulating one Cu nanoparticle with a 2-nm diameter in the water with the same volume fraction. Therefore, it can be concluded that the particle aggregation has no effect on the results.
Conclusion
In this paper, the specific heat capacities of the Cu-water nanofluids with different volume fractions were determined using MD simulation. The MD results were validated with experimental data for the specific heat of pure water and pure copper. The specific heat of nanofluid was found to decrease with the increase in the volume fraction of copper nanoparticles. It was also observed that the MD results are in good agreement with the thermal equilibrium model for predicting the specific heat of nanofluids, and the other model based on the mixing theory for ideal gas mixtures failed to predict the specific heat of nanofluids.
Abbreviations
- c p :
-
Specific heat capacity
- E :
-
Energy
- k B :
-
Boltzmann constant
- r :
-
Inter-atomic distance
- T :
-
Temperature
- φ :
-
Nanoparticle volumetric fraction
- ρ :
-
Density
- ε :
-
LJ energy
- σ :
-
Length parameter in LJ
- bf :
-
Base fluid
- nf :
-
Nanofluid
- n :
-
Nanoparticle.
References
Murshed SMS, Leong KC, Yang C: Enhanced thermal conductivity of TiO 2 -water based nanofluids. Int J Therm Sci. 2005, 44: 367–373. 10.1016/j.ijthermalsci.2004.12.005
Zhang X, Gu H, Motoo F: Effective thermal conductivity and thermal diffusivity of nanofluids containing spherical and cylindrical nanoparticles. Exp Therm Fluid Sci. 2007, 31: 593–599. 10.1016/j.expthermflusci.2006.06.009
Zeinali Heris S, Etemad SG, Nasr Esfahany M: Experimental investigation of oxide nanofluids laminar flow convective heat transfer. Int Comm Heat Mass Tran. 2006, 33: 529–535. 10.1016/j.icheatmasstransfer.2006.01.005
Kim H, Kim J, Kim MH: Effect of nanoparticles on CHF enhancement in pool boiling of nano-fluids. Int J Heat Mass Tran. 2006, 49: 5070–5074. 10.1016/j.ijheatmasstransfer.2006.07.019
Saidur R, Leong KY, Mohammad HA: A review on applications and challenges of nanofluids. Renew. Sustain. Energy Rev. 2011, 15: 1646–1668. 10.1016/j.rser.2010.11.035
Li XF, Zhu DS, Wang XJ, Wang N, Gao JW, Li H: Thermal conductivity enhancement dependent pH and chemical surfactant for Cu-H 2 O nanofluids. Thermo chimica Acta. 2008, 469: 98. 10.1016/j.tca.2008.01.008
Moghadassi AR, Masoud Hosseini S, Henneke D, Elkamel A: A model of nanofluids effective thermal conductivity based on dimensionless groups. J Therm Anal Calorimetry. 2009, 96: 81. 10.1007/s10973-008-9843-z
Teng TP, Hung YH, Teng TC, Mo HE, Hsu HG: The effect of alumina/water nanofluid particle size on thermal conductivity. Appl Therm Eng 2010, 30: 2213. 10.1016/j.applthermaleng.2010.05.036
Meibodi ME, Vafaie-Sefti M, Rashidi AM, Amrollahi A, Tabasi M, Sid Kalal H: Simple model for thermal conductivity of nanofluids using resistance model approach. Int Comm Heat Mass Tran. 2010, 37: 555. 10.1016/j.icheatmasstransfer.2009.12.010
Hojjat M, Etemad SG, Bagheri R, Thibault J: Rheological characteristics of non-Newtonian nanofluids: Experimental investigation. Int Comm Heat Mass Tran. 2011, 38: 144. 10.1016/j.icheatmasstransfer.2010.11.019
Talaei Z, Mahjoub AR, Rashidi AM, Amrollahi A, Meibodi ME: The effect of functionalized group concentration on the stability and thermal conductivity of carbon nano tube fluid as heat transfer media. Int Comm Heat Mass Tran. 2011, 38: 513. 10.1016/j.icheatmasstransfer.2010.12.035
Yu W, Xie H, Wang X, Wang X: Significant thermal conductivity enhancement for nanofluids containing grapheme nano sheets. Phys Lett. 2011, 375: 1323. 10.1016/j.physleta.2011.01.040
Pak BC, Cho YI: Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp Heat Tran. 1998, 11: 151. 10.1080/08916159808946559
Hwang KS, Jang SK, Choi SUS: Flow and convective heat transfer characteristics of water-based Al2O3 nanofluids in fully developed laminar flow regime. Int J Heat Mass Tran. 2009, 52: 193. 10.1016/j.ijheatmasstransfer.2008.06.032
Maigaa SEB, Nguyena CT, Galanisb N, Roya G: Heat transfer behaviors of nanofluids in a uniformly heated tube. Superlattices and Micro structures. 2004, 35: 543. 10.1016/j.spmi.2003.09.012
Maiga SEB, Palm SJ, Nguyen CT, Roy G, Galanis N: Heat transfer enhancement by using nanofluids in forced convection flows. Int J Heat Fluid Flow. 2005, 26: 530. 10.1016/j.ijheatfluidflow.2005.02.004
Palm SJ, Roy G, Nguyen CT: Heat transfer enhancement with the use of nanofluids in radial flow cooling systems considering temperature-dependent properties. Appl Therm Eng. 2006, 26: 2209. 10.1016/j.applthermaleng.2006.03.014
Hwang KS, Lee JH, Jang SP: Buoyancy-driven heat transfer of water-based Al2O3 nanofluids in a rectangular cavity. Int J Heat Mass Tran. 2007, 50: 4003. 10.1016/j.ijheatmasstransfer.2007.01.037
Behzadmehr A, Saffar-Avval M, Galanis N: Prediction of turbulent forced convection of a nanofluid in a tube with uniform heat flux using a two phase approach. Int J Heat Fluid Flow. 2007, 28: 211. 10.1016/j.ijheatfluidflow.2006.04.006
Polidori G, Fohanno S, Nguyen CT: A note on heat transfer modeling of Newtonian nanofluids in laminar free convection. Int J Therm Sci. 2007, 46: 739. 10.1016/j.ijthermalsci.2006.11.009
Lee J, Mudawar I: Assessment of the effectiveness of nanofluids for single-phaseand two-phase heat transfer in micro-channels. Int J Heat Mass Tran. 2007, 50: 452. 10.1016/j.ijheatmasstransfer.2006.08.001
Buongiorno J: Convective Transport in Nanofluids, ASME. J Heat Tran. 2006, 128: 240. 10.1115/1.2150834
Tiwari RK, Das MK: Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int J Heat Mass Tran. 2007, 50: 2002. 10.1016/j.ijheatmasstransfer.2006.09.034
Ho CJ, Chen MW, Li ZW: Numerical simulation of natural convection of nanofluid in a square enclosure: Effects due to uncertainties of viscosity and thermal conductivity. Int J Heat Mass Tran. 2008, 51: 4506. 10.1016/j.ijheatmasstransfer.2007.12.019
Heyhat MM, Kowsary F: Effect of Particle Migration on Flow and Convective Heat Transfer of Nanofluids Flowing Through a Circular Pipe, ASME. J Heat Tran. 2010, 132: 062401. 10.1115/1.4000743
Kowsary F, Heyhat MM: Numerical Investigation into the Heat Transfer Enhancement of Nanofluids Using a Non-homogeneous Model. J. Enhanced Heat Transfer. 2011, 18: 81–90. 10.1615/JEnhHeatTransf.v18.i1.70
Zhou SQ, Ni R: Measurement of the specific heat capacity of water-based Al 2 O 3 nanofluid. Appl Phys Lett. 2008, 92: 093123. 10.1063/1.2890431
Vajjha RS, Das DK: Specific Heat Measurement of Three Nanofluids and Development of New Correlations, ASME. J Heat Tran. 2009, 131: 071601. 10.1115/1.3090813
Zhou LP, Wang BX, Peng XF, Du XZ, Yang YP: On the Specific Heat Capacity of CuO Nanofluid. Adv Mech Eng. 2010, 172085.
Allen MP, Tildesley DJ: Computer Simulations of Liquids Clarendon. Oxford; 1987.
Frenkel D, Smit B: Understanding Molecular Simulation; Algorithms to Applications. Academic Press, Cornwall, UK; 1996.
Rahman A, Stillinger FH: Molecular dynamics study of liquid water. J Chem Phys. 1971., 33:
Keblinski P, Phillpot SR, Choi SUS, Eastman JA: Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int J Heat Mass Tran. 2002, 45: 855. 10.1016/S0017-9310(01)00175-2
Vladkov M, Barrat JL: Modeling Transient Absorption and Thermal Conductivity in a Simple Nanofluid. Nano Lett. 2006, 6: 1224. 10.1021/nl060670o
Sarkar S, Selvam RP: Molecular dynamics simulation of effective thermal conductivity and study of enhanced thermal transport mechanism in nanofluids. J. Appl. Phys. 2007, 102: 074302. 10.1063/1.2785009
Sankar N, Mathew N, Sobhan CB: Molecular dynamics modeling of thermal conductivity enhancement in metal nanoparticle suspensions. Int Comm Heat Mass Tran. 2008, 35: 867. 10.1016/j.icheatmasstransfer.2008.03.006
Li L, Zhang Y, Ma H, Yang M: Molecular dynamics simulation of effect of liquid layering around the nanoparticle on the enhanced thermal conductivity of nanofluids. J Nanopart Res. 2010, 12: 811. 10.1007/s11051-009-9728-5
Evans W, Fish J, Keblinski P: Role of Brownian motion hydrodynamics on nanofluid thermal conductivity. Appl Phys Lett. 2006, 88: 093116. 10.1063/1.2179118
Lu WQ, Fan QM: for the particle’s scale effect on some Thermophysical properties of nanofluids by a simplified molecular dynamics method. Eng Anal Bound Elem. 2008, 32: 282. 10.1016/j.enganabound.2007.10.006
Galliero G, Volz S: Thermo diffusion in model nanofluids by molecular dynamics simulations. J. Chem. Phys. 2008, 128: 064505. 10.1063/1.2834545
MacKerell AD, Bashford D, Bellot RL, Dunbrack RL, et al.: J. Phys. Chem.. 1998, 102: 3586. 10.1021/jp973084f
Hoover WG: Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A. 1985, 31: 1695–1697. 10.1103/PhysRevA.31.1695
Hoover WG: Constant-pressure equations of motion. Phys. Rev. A. 1986, 34: 2499–2500. 10.1103/PhysRevA.34.2499
Melchionna S, Ciccotti G, Holian BL: Hoover NPT dynamics for systems varying in shape and size. Mol Phys. 1993, 78: 533–544. 10.1080/00268979300100371
Plimpton S: Fast Parallel Algorithms for Short-Range Molecular Dynamics. J Comp Phys. 1995, 117: 1. 10.1006/jcph.1995.1039
Plimpton SJ, Pollock R, Stevens M Proc of the Eighth SIAM Conference on Parallel Processing for Scientific Computing. In Mesh Ewald and rRESPA for Parallel Molecular Dynamics Simulations. Minneapolis, MN; 1997.
Landau LD, Lifshitz EM: Statistical Physics. Butterworth-Heinemann; 1980.
Allen MP, Tildesley DJ: Computer simulation of liquids. Oxford University Press; 1989.
Li L, Zhang Y, Ma H, Yang M: An investigation of molecular layering at the liquid–solid interface in nanofluids by molecular dynamics simulation. Phys Lett. 2008, 372: 4541. 10.1016/j.physleta.2008.04.046
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AR led and involved in the MD simulation, manuscript preparation and interpretation of the results. FYA generated the proper lattice and MD simulation code. MMH as the corresponding author acted as initiating the idea, manuscript preparation and data elucidation. KG participated in numerical run procedure.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rajabpour, A., Akizi, F.Y., Heyhat, M.M. et al. Molecular dynamics simulation of the specific heat capacity of water-Cu nanofluids. Int Nano Lett 3, 58 (2013). https://doi.org/10.1186/2228-5326-3-58
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2228-5326-3-58