Simulation of SnO₂/WO₃ nanofilms for alcohol of gas sensor based on metal dioxides: MC and LD studies

Abstract

This work presents a study of the adsorption properties of nanostructures. The moving gas technique was employed to determine the transient and steady-state response behavior of nanocrystalline gas sensors. SnO₂ sensors have shown high sensitivity to low concentrations of ethanol at moderate temperature. Tin dioxide is the most used material for gas sensing because its three-dimensional nanofilms and properties are related to the large surface exposed to gas adsorption. This study proposes the use of SnO₂ nanofilms in interaction with ethanol; we used different percentages of SnO₂ and WO₃ in the adsorption of ethanol by nanofilms. The total energy, potential energy, and kinetic energy were calculated for the interaction between nanofilms and ethanol at different concentrations and at 300 K. The calculations were achieved by Langevin dynamics and Monte Carlo simulation methods. The total energy decreased with additional tungsten percentage in the nanofilms and increased with additional number of ethanol molecules and interactions between them are endothermic.

Background

It has been suggested that nanometer-sized particles, if properly treated, can be used to form high-surface-area catalysts, efficiencies of which improve on existing catalytic function or sensor function[1, 2]. This might further be improved through changes in molecular electronic structure and as a result of the development of confined regions that accompany the transition to the macroscopic regime for both the active elements and their substrate supports[3]. In this paper, we used tin dioxide because it presents great potential properties for applications such as optoelectronic devices, gas sensors, and solar energy or even for detecting leakages of reducing gases such as H, H₂S, CO, and others[4].

Solids with a grain size of a few nanometers are normally referred to as nanocrystalline materials: they exhibit properties that are significantly different from their coarse-grained polycrystalline counterparts. A first classification of the change in the properties of a material relies on either ‘bulk’ or ‘surface’ effects. Typically, bulk effects involve the confinement of electrons in nanometric cells, which causes quantum phenomena to take place[5]. Surface effects normally appear because of the magnification of the specific surface of nanostructures, leading to the enhancement of the properties related to that, such as catalytic activity or surface adsorption[6].

Developing new solid-state gas sensors with improved properties carries with it an obvious close relationship between the sensing performance of the active materials and their surface chemical activity. The theoretical study of such surface adsorption interactions provides a valuable tool to get superior performances that are unattainable using only a trial-and-error approach together with a powerful analytic methodology to explain the experimental data. Tin dioxide (SnO₂) plays a key role as one of the more representative sensing materials in solid-state gas sensors[7], presenting a significant surface reactivity with many important reducing (CO, NO) and oxidizing gases (O₂, NO₂)[8, 9].

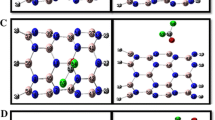
However, to explain the sensing behavior, it is necessary to keep in mind that there exist interfering processes poisoning the surface[10] and that these can dramatically change the effective adsorptions of the target species and therefore their eventual detection as in the case of the SnO₂ surface[11, 12]. Thus, in the present analysis, their effects have also been studied in order to point up their consequences on the sensing mechanisms[13, 14]. In this paper, we used SnO₂ nanofilms with different replication counts in the (i.j.k) plane that are shown in Figure1. After structural characterizations, photoluminescence characteristics of the SnO₂ nanofilms were studied, so some tin atoms were replaced by tungsten atoms of different percentages in nanofilms (Figure2).

Figure 1

Optimized configuration (top view) of SnO ₂ nanofilm replication count in ( i . j . k ) planes of the surface. (a) (1.1.2) with chirality (3,3), (b) (1.1.2) with chirality (6,6), (c) (1.1.4) with chirality (3,3), (d) (1.1.4) with chirality (6,6).

Figure 2

Sn and W dioxide nanofilms with different percentages for nanofilm (1.1.4) with chirality (6,6). (a) 20% (W/Sn), (b) 40% (W/Sn), (c) 60% (W/Sn), (d) 80% (W/Sn).

Nowadays, first-principles methodologies are based on using Langevin dynamics to simulate the presence of a solvent during annealing and Monte Carlo simulation to sample configurations from a Boltzmann-weighted distribution. Langevin dynamics and Monte Carlo simulation can provide precise calculations of the total energy and potential energy of adsorption. Moreover, faster codes and new computational facilities allow dealing with numbers of surface adsorption configurations in moderate computing times. In this context, the aim of the present work is to provide theoretical hints for the development of improved C₂H₅OH gas sensors using SnO₂ and WO₃ as base sensing materials, and an interaction pattern between nanofilms and 45 molecules of ethanol in a mean distance of 13 Å is shown in Figure3. The relevance of surface orientation is discussed, and the most significant adsorption sites of C₂H₅OH are identified.

Figure 3

Interaction between SnO ₂ nanofilm (1.1.4) with chirality (6,6) and 45 ethanol molecules in gas phase.

Results and discussion

Semiconducting sensors offer an inexpensive and simple method for monitoring gases. The change of the electrical conductivity of semiconducting materials upon exposure to a reducing gas such as C₂H₅OH has been used for gas detection. Therefore, nanofilms have been utilized as a sensing material in pressure, flow, thermal, gas, optical, mass, position, stress, strain, chemical, and biological sensors. The sensor was based on the principle that the electronic properties of Sn and W nanofilms change when subjected to strains. The isotropic nature of nanofilms helps in measuring strains in multiple locations and in different directions. This manuscript demonstrated, using first-principles quantum transport calculations and Langevin dynamics (LD) and Monte Carlo (MC) simulation methods, that hydrostatic pressure can induce radial deformation and therefore electrical transition of Sn-W nanofilms. The measurements were carried out in a humid air atmosphere, which has the same condition as that of a general operation of a sensor. The total energy, potential energy, and kinetic energy were calculated for the interaction of Sn and W dioxide nanofilms and different numbers of ethanol molecules at 300 K. The calculations are shown in Tables1,2,3,4,5, and6, which show that with additional number of ethanol molecules, the energies increased. Figure4 shows that the total energy increased with additional distance mean of ethanol molecules and its number is related to Sn-W nanofilms.

Table 1 E _total , E _pot , and E _kin calculated for SnO ₂ nanofilms (1.1.2) with chirality (3,3) and chirality (6,6)

Table 2 E _total , E _pot , and E _kin calculated for SnO ₂ nanofilms (1.1.4) with chirality (3,3) and chirality (6,6)

Table 3 E _total , E _pot , and E _kin calculated for different percentages of SnO ₂ /WO ₃ nanofilms (1.1.2) with chirality (3,3)

Table 4 E _total , E _pot , and E _kin calculated for different percentages of SnO ₂ /WO ₃ nanofilms (1.1.2) with chirality (6,6)

Table 5 E _total , E _pot , and E _kin calculated for different percentages of SnO ₂ /WO ₃ nanofilms (1.1.4) with chirality (3,3)

Table 6 E _total , E _pot , and E _kin calculated for different percentages of SnO ₂ /WO ₃ nanofilms (1.1.4) with chirality (6,6)

Figure 4

Total energy (kcal/mol) calculated for interaction of SnO ₂ and ethanol molecules at 300 K. (a, b) Nanofilm (1.1.2) with chirality (3,3), (c, d) nanofilm (1.1.4) with chirality (3,3).

The characteristics of the sensor were investigated by changing of resistance in ethanol ambient with different products in air. Formation of acetaldehyde by the oxidative dehydrogenation of ethanol depends critically upon the reaction step that requires the oxide surface to acquire a negative charge: when ethanol is injected into the micro-reactor containing either a pure nanofilm compound or a large fraction of ethanol, it was found to be transformed to acetaldehyde. It then may be adsorbed in the form of ethoxide (CH₃CH₂O), producing an adsorbed hydrogen atom. On the contrary, this may be transformed to acetaldehyde (CH₃CHO), forming an adsorbed hydrogen atom:

$$\begin{array}{l}{\text{CH}}_3{\text{CH}}_2{\text{OH}}_{\left(\text{g}\right)}\to {\text{CH}}_3{\text{CH}}_2{\text{O}}_{\text{ads}}+{\text{H}}_{\text{ads}}\hfill \\ {\text{CH}}_3{\text{CH}}_2{\text{O}}_{\text{ads}}\to {\text{CH}}_3{\text{CHO}}_{\text{ads}}+{\text{H}}_{\text{ads}}\hfill \\ {\text{H}}_{\text{ads}}+{\text{H}}_{\text{ads}}\to {2\text{H}}_{\text{ads}}^{+}+2e^{-}\hfill \end{array}\text{.}$$

The thermodynamic properties of this interaction are calculated by LD and MC simulation methods that are shown in Tables1,2,3,4,5, and6. Now, in the reaction environment, there are ethanol and acetaldehyde, from which methyl ethyl ketone represents the second most important reaction product in our calculations. This reaction requires H transfer from one adsorbed acetaldehyde, which becomes oxidized, to another adsorbed ethanol, which is reduced to alkoxide. Some Sn atoms are replaced by W atoms, making different nanofilms for the adsorption of ethanol molecules in gas phase. The energies of interaction are calculated by Langevin dynamics and Monte Carlo simulation that are shown in Tables1,2,3,4,5, and6. It was also found that the reduction in Sn atoms and length enhances the sensitivities of the sensors.

The trajectories obtained by applying this algorithm agree with those obtained by Langevin dynamics simulations. The efficiency of a Monte Carlo-based search engine depends on the interplay of the energy update protocol and the type of conformational movements used to modify a given conformation. The total energy and potential energy are approximating similarly in both methods with additional distance mean. On the other hand, the kinetic energy is changed with additional distance for the Langevin dynamics method, but it is the same for the Monte Carlo simulation. With increased W in nanofilms, the total energy decreased at 300 K as shown in Figure5 and Tables1,2,3,4,5, and6.

Figure 5

Total energy (kcal/mol) calculated for interaction of nanofilms and ethanol molecules at different percentages (W/Sn).

Conclusions

It is believed that nanofilm-incorporated sensors can bring dramatic changes to the biomedical industry. There are certain cases such as diabetes where regular tests by patients themselves are required to measure and control the sugar level in the body. The SnO₂ and WO₃ chemical sensors for liquids can be used for blood analysis (for example, detecting sodium or finding pH value). Sensors and biosensors have been widely used in the food industry to provide safety and quality control of food products as the contamination of foods caused by bacterial pathogens may result in numerous diseases.

The sensitivity could be measured when the detecting gas is mixed homogeneously with air. The sensitivity depends on the ethanol concentration at each work temperature. The sensitivity increases with increasing ethanol gas concentration. The response and sensitivity of the alcohol-treated sensor are found to be very high when compared to those of the air-treated sensor. The total energy depends linearly on the temperature in that it increased with additional temperature, so this interaction is endothermic.

The total energy in the two methods decreased initially, but it increased with additional number of ethanol molecules that have indicated interaction between SnO₂ nanofilms. The percentages of WO₃ were increased in the nanofilms, so the total energy decreased which indicated that the nanofilms stabled upon adsorption. The diffusion behavior can be clearly distinguished as either normal mode or single file mode in time scales of about 1,000 ps. It is possible to show that setting a threshold of 1 on the movement of the dihedrals of the backbone in a single Monte Carlo step, the mean quantities associated with the off-equilibrium dynamics are well reproduced, while the good description of higher moments requires smaller moves.

Methods

Langevin dynamics simulation

In this work, we use Langevin dynamics and Monte Carlo simulation methods for calculation of interaction systems. The Langevin dynamics method simulates the motion of molecules subjected to random collisions and frictional forces and can be used to model solvated systems without explicitly including solvent molecules[15]. It provides information on the time evolution of the molecular system. A Langevin dynamics simulation is set up in much the same way as a molecular dynamics simulation, with small differences due to the addition of the friction coefficient. Langevin dynamics is similar in principle to regular molecular dynamics. It includes frictional effects to simulate the presence of a solvent implicitly, where regular molecular dynamics requires inclusion of explicit solvent molecules. One term represents a frictional force, and the other, a random force$\overrightarrow{R}$. For example, the effects of solvent molecules not explicitly present in the system being simulated would be approximated in terms of a frictional drag on the solute as well as random kicks associated with the thermal motions of the solvent molecules. Since friction opposes motion, the first additional force is proportional to the particle's velocity and oppositely directed. Langevin's equation for the motion of atom i is[16]:

$$\overrightarrow{F_i}-{\gamma }_i{\overrightarrow{\upsilon }}_i+{\overrightarrow{R}}_i\left(t\right)=m_i{\overrightarrow{a}}_i\text{,}$$

(1)

where$\overrightarrow{F_i}$ is still the sum of all forces exerted on atom i by other atoms explicitly present in this system. This equation is often expressed in terms of the collision frequency ζ = γ/m. The friction coefficient is related to the fluctuations of the random force by the fluctuation-dissipation theorem:

$$〈{\overrightarrow{R}}_i\left(t\right)〉=0\text{,}{\displaystyle \int 〈{\overrightarrow{R}}_i\left(0\right).{\overrightarrow{R}}_i\left(t\right)〉dt=6K_{\text{B}}T{\gamma }_i}\text{.}$$

(2)

In simulations, it is often assumed that the random force is completely uncorrelated at different times, that is, the above equation takes the form:

$$〈{\overrightarrow{R}}_i\left(t\right).{\overrightarrow{R}}_i\left(t^{\prime }\right)〉dt=6K_{\text{B}}T{\gamma }_i\delta \left(t-t^{\prime }\right)\text{.}$$

(3)

The temperature of the system being simulated is maintained via this relationship between$\overrightarrow{R}\left(t\right)$ and γ. The jostling of a solute by a solvent can expedite barrier crossing, and hence, Langevin dynamics can search conformations better than Newtonian molecular dynamics (γ = 0).

The Monte Carlo method samples phase space by generating random configurations from a Boltzmann distribution at a given temperature. Averages computed from a properly equilibrated Monte Carlo simulation correspond to thermodynamic ensemble averages. Thus, the Monte Carlo method can be used to find average energies and equilibrium structural properties of complex interacting systems[17]. A sequence of successive configurations from a Monte Carlo simulation constitutes a trajectory in phase space[18, 19]. The Monte Carlo method provides a more direct route to equilibrium structural and thermodynamic properties. However, these calculations can be quite long, depending upon the system studied[20]. Because of imperfections of the force field, the lowest energy base usually does not correspond to the native state in most cases, so the rank of native structure in those decoys produced by the force field itself is poor. Therefore, the rank of native structure can be relatively better when ranked by the second force field[21–23]. The acceptance ratio is a running average of the ratio of the number of accepted moves to attempted moves. Optimal values are close to 0.5; varying the step size can have a large effect on the acceptance ratio.