Abstract
Background
Advances in ultrasonic telemetry, including the ability to accurately position a transmitter within an array of hydrophone receivers, have led to increased opportunities to investigate a broad spectrum of ecological questions in aquatic systems. The quality and efficiency of positioning a transmitter relies upon factors controlled by the researcher (for example, geometry of the receiver array) as well as environmental conditions (for example, water quality or environmental noise). While the physics of sound wave propagation are well understood, the high amount of environmental variability in and among aquatic habitats makes it difficult to predict exactly how any given ultrasonic signal will behave. To evaluate variability in system performance across different receiver arrays in diverse environments we present positional records for fixed-location tags recorded with a popular positioning array, the VEMCO Positioning System (VPS). Using these records we evaluate the relationships between system performance, measured as both horizontal positioning error and positioning efficiency, and user-controlled and environmental variables. We used generalized linear mixed models to assess performance at a coastal site, a site in a freshwater tidal estuary, and a riverine site.
Results
The positioning errors were similar across sites, with median errors ranging from 1.6 to 3.3 m. In contrast, there was large variation in positioning efficiency across sites, with poor positioning efficiency in the coastal habitat (7%), possibly due to high levels of bioacoustic noise, and moderate efficiency in the river (21%) and estuary habitats (27%). Our statistical models indicate that array geometry was consistently the most important predictor of positioning performance. Environmental noise and water movement also emerged as additional predictors of performance at several sites.
Conclusions
The results provide insight into VPS performance capabilities and emphasize the importance of testing array geometries. Additionally, water quality parameters should be monitored and receiver mooring designs should be carefully considered before embarking upon a telemetry study. We hope this work will guide future researchers in creating more effective designs for positioning arrays, and facilitate the collection of high quality information about movement and behavior patterns of aquatic organisms.
Similar content being viewed by others
Background
Animal movement is fundamental to much of ecology and animal biology [1]. Organisms must move to find food, avoid predators, encounter mates, and respond to the environment. Thus knowing the fine-scale movement of targeted animals is an important aspect of understanding their habitat use and ecology. Ultrasonic telemetry allows for the monitoring of movement in aquatic environments, which can otherwise be difficult to observe [2, 3]. Approaches can be varied, ranging from simple detections of animal presence at stationary receivers (for example, [4–6]) to detailed recording of animal positions and three-dimensional acceleration [7–9]. Telemetry systems can collect fine-scale positions of transmitters when receivers are deployed in an array, and the differences in the arrival time of a single transmission at multiple receivers are used to calculate its position [10–14]. Recent development of precision timing mechanisms and autonomous receivers with long battery lives have allowed for the deployment of flexible, long-term positioning arrays for research in varied aquatic ecosystems [15, 16].
The quality and efficiency of positioning by telemetry systems relies upon variables controlled by the researcher as well as upon environmental conditions. The conceptual model in Figure 1 summarizes how user-controlled and environmental variables may influence sound propagation and the performance of a positioning system. User-controlled variables include, but are not limited to, the geometry of the receiver array, the estimated speed of sound at the study site, and the receiver mooring design. The geometry of the receivers and transmitters has been shown to affect system performance [12, 16–19], likely due to the spatial variability in mathematical certainty inherent in triangulation equations [20, 21]. Inaccurate estimates of the speed of sound (which varies with temperature and conductivity) and movement or tilt of receivers can also result in increased positioning error. Additionally, environmental variables can directly impact the propagation of a sound wave or mask the signal with non-target noise. As waves spread from a point source acoustic energy is reduced, and the wave can be reflected, refracted, scattered, and/or absorbed by elements in the environment [20]. Loss or alteration of the sound wave can result in an incomplete or erroneous signal arriving at the receiver. In addition, high levels of environmental noise due to human activity or natural processes may reduce the ability of receivers to detect and extract the information in an ultrasonic signal [3, 20–22]. Given the inherent variability of real-world environments, it is difficult to predict exactly how each sound wave will behave and thus how a positioning system will perform at any given research site. However, by examining the performance of several positioning systems with varying array geometries and environmental factors we can better understand which conditions are most likely to pose challenges in future studies.
Conceptual model of factors influencing the performance of an ultrasonic positioning system. Positioning system performance metrics (a) are directly influenced by various user-controlled and environmental variables (b), which in turn are influenced by a number of contributing factors present at a study site (c). Variables measured for this study are bold. Those in gray could not be reliably measured so were not considered in statistical models.
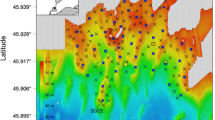
In order to evaluate the variability in system performance across diverse study sites, we assessed transmitter locations recorded with an increasingly popular positioning array, the VEMCO Positioning System (hereafter VPS; VEMCO Division of AMIRIX Systems; Halifax, Nova Scotia, Canada), which were collected in pursuit of three separate research objectives in three different environments [23], Steel et al. unpublished observations, Thomas et al. unpublished observations. These environments encompass a broad spectrum of aquatic habitats where ultrasonic telemetry is frequently utilized: oceans, estuaries, and rivers. The oceanic site was located on the coastal shelf off San Diego, California within the Point Loma kelp forest (32.691°, -117.263°), and was designed to monitor movement of pink abalone (Haliotis corrugata) away from an artificial spawning aggregation site. The estuarine site was in a shallow tidal lagoon known as Mildred Island (37.975°, -121.530°) in the freshwater portion of the San Francisco Estuary, near the town of Stockton, California. It was intended to document the habitat use of largemouth bass (Micropterus salmoides) in areas of high submerged aquatic vegetation. The riverine site was in the Sacramento River at the confluence with Antelope Creek (40.082°, -122.116°), south of the town of Red Bluff, California (Figure 2), and was deployed to record the habitat use of spawning green sturgeon (Acipenser medirostris). For more information about the study sites and array deployment, refer to the methods. The designs of the positioning arrays varied by site, but all included transmitters in fixed locations that were used to assess both the horizontal positioning error (quantified as the Euclidian distance between the GPS location of a fixed tag and the VPS-calculated positions) and the efficiency of positioning (quantified as the proportion of the expected transmissions that were recorded as positions). To achieve our primary objective of assessing VPS performance, we modeled the relative importance of user-controlled and environmental variables (Table 1) on positioning error and efficiency within these three disparate aquatic environments.
Location of VPS study areas. The three VPS arrays were located (a) in a coastal kelp forest on the continental shelf of southern California, (b) in the tidal freshwater portion of the San Francisco estuary, and (c) in the main channel of the Sacramento River in the Central Valley of northern California. Sites contained six to 10 independent hydrophone receivers (Vemco VR2W) and six to 13 coded transmitters (Vemco 69 kHz). Transmitters were moored in known, fixed locations either independently or co-located with a receiver. Number of recorded positions (N pos) of each transmitter are displayed at right by transmitter reference code (Trns). Base maps from Esri (DigitalGlobe, GeoEye, i-cubed, USDA, USGS, AEX, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community).
Results
Tag detection
The positional data were recorded over approximately equal time spans at each site (49 to 60 days), but the number of fixed transmitters and the quantity of recorded positions varied by site and by transmitters within sites (Figure 2). Over the 60-day study period for the coastal site, 4,266 positions were recorded from six V9-2H transmitters with 450 to 500 s random delays (11.9 positions recorded per transmitter-day). At the estuarine site a subset of 40 days were selected for analysis at eight even intervals within the 340 days the array was in place (see methods for further explanation of sampling constraints). Over the reduced study period, 38,498 positions were recorded from 10 V13-1L transmitters with 600 to 800 s random delays and three V13-1L transmitters with 170 to 310 s random delays (averaging 74.0 positions recorded per transmitter-day). Over the 49-day study period for the riverine array, 7,735 positions were recorded from five V13-1H transmitters and one V16-1H transmitter, all with 600 to 800 s random delays (averaging 26.3 positions recorded per transmitter-day).
Array performance
The magnitudes and distribution of horizontal positioning errors were similar across the three sites (Figure 3a). The most noteworthy difference was in the coastal site where the distribution of error showed a bimodal pattern with peaks at 0.9 and 3.5 m, and a larger median error (median = 3.3 m, 95%ile = 7.3 m) as compared to the estuarine (median = 2.5 m, 95%ile = 15.8 m) or riverine sites (median = 1.6 m, 95%ile = 7.9 m). There were more pronounced differences across sites for positioning efficiency (Figure 3b). The coastal site had low median efficiency and a narrow probability density (median = 0.02, 95%ile = 0.32). The estuarine site included a strong bimodal probability density with peaks at positioning efficiencies of 0.01 and 0.76, and it also had the highest median efficiency (median = 0.28, 95%ile = 0.42). The riverine site had a low median efficiency, similar to the coastal site, but the probability density included a slight bimodal pattern with the strongest peak where positioning efficiency equaled 0.01 and a weaker peak at 0.34 (median = 0.00, 95%ile = 0.79). Finally, it is important to note that individual transmitter locations within each study site showed a large amount of variability in positioning efficiency. For example, at the riverine site the two upstream transmitters were rarely positioned by the array (C-01: median = 0.0, 95%ile = 0.3; C-02: median = 0.0, 95%ile = 0.11) while the two in the center were recorded much more consistently (C-03: median = 0.54, 95%ile = 0.92; C-06: median = 0.69, 95%ile = 0.92).
Probability density functions of system performance metrics, by site. Estimated probability density functions for (a) horizontal positioning errors (defined as the distance between a transmitter’s fixed location and the location recorded by the positioning system) shown for all transmitter positions recorded (N positions: Coastal = 4,266; Estuarine = 38,498; Riverine = 7,735), and for (b) positioning efficiencies (defined as the proportion of expected transmissions that were recorded as positions during each 12 h interval of the study period) shown for each study site (N 12 h intervals: Coastal = 120; Estuarine = 80; Riverine = 98).
User-controlled variables
The geometry of the receiver array was summarized by the viewing angle, originally defined by Berge et al. [18]. It is calculated for each transmitter location as the angle between two bearings, running from the focal transmitter to the outer edges of the polygon formed by the receivers. This measure is referred to as ‘viewing’ angle because it is the angle required to view the entire receiver array from the perspective of the transmitter. A wide angle indicates that the tag is closer to the center of the array, and conversely a narrow angle indicates the tag is farther away. The range of viewing angles varied across sites with largest average angles at the coastal site (242 degrees) and smallest average angles at the riverine site (127 degrees). The viewing angle generally showed a clear bivariate relationship with positioning performance (Figure 4).
Bivariate relationship between array geometry and performance metrics, by site. Geometry of the positioning array was quantified by the viewing angle at each transmitter location. Viewing angle can be defined as the angle between two bearings running from the focal transmitter to the outer edges of the polygon formed by the receivers. Black lines show the linear fit between these viewing angles and each of the performance metrics, horizontal positioning error and positioning efficiency, using ordinary least squares regression.
Environmental variables
For the coastal array, a visual assessment of time series plots suggested that environmental variables are related to positioning performance. The winds generally came from the south and west during the period from 23 September to 27 November 2009 when the coastal array was in place (Figure 5c). The wind contributed to waves ranging in height from 0.5 to 2 m, with two distinct periods of large waves reaching up to 3.5 m (Figure 5d). The dominant wave period varied between 10 and 20 s in a rhythmical manner (Figure 5e) while the average wave period over 20 min intervals varied from 6 to 9 s, increasing towards the end of the study (Figure 5f). The water temperature decreased, although intermittently, from 20.5°C on 23 September to 17.0°C on 27 November with slightly lower temperatures at the beginning of November (Figure 5g). In general, the positioning efficiency was highest during late September and early October, during a period of more southerly winds, lower waves, warmer temperatures, and shorter average wave periods (Figure 5b). We also saw a noticeable drop in positioning efficiency corresponding with the largest spike in wave height and a rapid drop in water temperature during the last week of October. Positioning errors became more variable in November when the site experienced westerly winds, greater average wave periods, and cooler water temperatures (Figure 5a).
Time series of performance metrics and environmental variables for the coastal array. Measurements of (a, b) performance metrics and (c-g) environmental variables during the study period from 24 September to 27 November 2009. The yellow line in (b) shows the daily mean positioning errors during the daytime period (7:00 to 19:00), while the grey line shows the daily mean positioning errors during the night period (19:00 to 7:00). For data sources, see text.
At the estuarine site there were also noticeable patterns among the environmental variables and array performance. During the deployment period from 2 September 2009 to 9 August 2010 the predominant flow direction was upriver due to tidal forcing and water extractions, with an exception in April and May when river outflow dominated (Figure 6c). Because inorganic dissolved solids are contributed both as ocean salinity and agricultural run-off in river inputs, we saw multiple peaks in electrical conductivity that corresponded both with tidal forcing in January and river outflow in May (Figure 6d). Water temperatures were highly seasonal, ranging from less than 10°C in winter to almost 25°C in summer (Figure 6e). The temperature and seasonality also drove the abundance of submerged aquatic vegetation at the site (Figure 6f). In general, we saw the greatest positioning error during peaks of discharge and conductivity in April and May (Figure 6a). Positioning efficiency was relatively stable over the study period, with greater variability during the spring and summer months coinciding with increasing temperatures, greater river outflow, and growth of aquatic macrophytes (Figure 6b).
Time series of performance metrics and environmental variables for the estuarine array. Measurements of (a, b) performance metrics and (c-f) environmental variables during the study period from 2 September 2009 to 9 August 2010. Performance metrics were only calculated for discrete 5-day intervals to correspond with sampling of macrophytes. Dotted lines show linear interpolation between these 5-day intervals while vertical grey bars in (c) through (e) indicate the corresponding time periods in plots of other environmental metrics. The yellow line in (b) shows the daily mean positioning errors during the daytime period (7:00 to 19:00), while the gray line shows the daily mean positioning errors during the night period (19:00 to 7:00). For data sources, see text.
The relationship between environmental variables and performance metrics appears strongest at the riverine site. At the beginning of the study period on 11 April 2012 there was a high flow event where the river stage rose more than 0.5 m (1.7 ft) in 12 h (Figure 7c). This triggered a spike in turbidity (Figure 7d) and a drop in water temperature (Figure 7e). In addition to this event, a smaller flow peak occurred in late April. Each of these higher flows corresponded with increases in the positioning error and sharp decreases in the positioning efficiency. The punctuations in flow interrupted a gradual increase in river stage between 10 April and 30 May 2009, accompanied by a gradual decrease in water temperatures (Figure 7c,e). During this time, positioning error became increasingly variable and positioning efficiency decreased in magnitude (Figure 7a,b).
Time series of performance metrics and environmental variables for the riverine array. Measurements of (a, b) performance metrics and (c-e) environmental variables during the study period from 10 April to 12 June 2012. Inclusion of a diel factor did not explain important differences in positioning performance at this site so positions from both day and night periods are combined in (b). For data sources, see text.
The diel period did not have an effect on positioning errors, but at some sites it did strongly influence positioning efficiency. At the coastal site, there was higher efficiency during the day (Mann-Whitney U test: P <0.0001; Figure 5) and at the estuarine site we saw the opposite pattern with higher efficiency at night (Mann-Whitney U test: P <0.0001; Figure 6). There was no significant difference in efficiency by diel period at the riverine site.
Statistical models
For each site full generalized linear mixed models (GLMMs) were constructed using horizontal positioning error (HPEm) or positioning efficiency as the response variable. A backwards step-wise selection process was subsequently used to identify those variables with the strongest relationships to performance. All models at all sites suggested an influence of viewing angle on performance (Table 2). For the models of HPEm we saw negative effects of viewing angle, where wider angles lead to smaller errors (Figure 8). However, for the models of positioning efficiency the coastal site included a surprising negative relationship with viewing angle, suggesting that when all other variables were controlled for, transmitters were positioned more frequently when they had narrower angles and were thus located farther from the center of the array. The model constructed for positioning efficiency at the estuarine site also suggested the same surprising negative relationship between viewing angle and frequency of recorded positions (Figure 9).
Predicted relationships between horizontal positioning error and explanatory variables. Individual panels show the relationship predicted from GLMM models for each variable remaining in the final site-specific models, when all other variables are held constant. The overall relationship of each variable is shown (thick colored line) as well as the relationship modeled for each fixed transmitter at a site (thin black lines), estimated with a random intercept term. The horizontal positioning error was modeled using a natural logistic transformation, but is plotted here in the original scale.
Predicted relationships between positioning efficiency and explanatory variables. Individual panels show the relationship predicted from GLMM models for each variable remaining in the final site-specific models, when all other variables are held constant. The overall relationship of each variable is shown (thick colored line) as well as the relationship modeled for each fixed transmitter at a site (thin black lines), estimated with a random intercept term. The positioning efficiency was modeled using a logit link function.
In addition to containing parameter estimates for array geometry, most final GLMMs also included variables describing water movement (that is, wave action, discharge, or river stage; Table 2). At the coastal site, the model of HPEm contained a parameter indicating a positive relationship between error and mean wave period (Figure 8). At the estuarine site, the final model for HPEm included a parameter for the absolute magnitude of discharge (selected to account for bidirectional tidal flows), but the overall effect size for this variable was small (Figure 8). At the riverine site, river stage, used as a proxy for water movement, showed a positive relationship with error in the final HPEm model. Notably, it was the only parameter other than array geometry in the model (Figure 8). For the final models of positioning efficiency, no parameter for water movement was included at the coastal site. However, at both the estuarine and riverine sites, water movement (measured as mean discharge and mean river stage, respectively) had a negative relationship with positioning efficiency, suggesting that when water movement was high transmitter positioning was more infrequent. The size of this effect was greater at the riverine site (Figure 9).
Three of the six final GLMMs included a two-level categorical variable for diel period, considered in model selection as a proxy for daily cycles of environmental noise. Consistent with the preliminary examination of variables, diel period was not particularly important for models of HPEm. It was only included in the final HPEm model for the coastal array, indicating that when all other variables were controlled for, positioning errors were slightly smaller during the night (Table 2). Diel period was retained in models of positioning efficiency at both the coastal and estuarine sites (Table 2). Model results confirm that more positions were recorded during the day in the coastal array, and that more positions were recorded at night in the estuarine array.
Aside from geometry, water movement, and diel period, the other parameters included in the final models represented water quality metrics such as temperature, electrical conductivity, or turbidity. Water temperature showed positive relationships with HPEm at both the coastal and estuarine sites, and electrical conductivity showed a very slight positive relationship with HPEm at the estuarine site (Figure 8). Water temperature showed a positive relationship with positioning efficiency at the coastal site, but a negative relationship with efficiency at both the estuarine and riverine sites. Turbidity was only included in the model for positioning efficiency at the riverine site, and was modeled as a negative relationship (Figure 9).
Discussion
Among the three arrays compared here, the median error in positions ranged from 1.6 to 3.3 m. These errors were calculated based on all recorded data, without any position filtering as is frequently done before fine-scale analysis of animal movements [19, 25]. This error range is smaller than the unfiltered mean error of 5 m (SD = 7.8 m) reported by Roy et al. [19] for a VPS deployed in a large hydropower reservoir. It is similar to the unfiltered mean error estimate of 2.6 m (SD = 2.3 m) reported by Espinoza et al. [16] for an estuary site, and larger than the filtered mean error range of 1.0 to 1.8 m reported by Andrews et al. [15] from a VPS placed in a protected ocean environment.
The positioning efficiencies were calculated at 12-h intervals for each transmitter across sites (see methods for more information). The median site-level values ranged from 0.0 to 0.28 positions recorded per transmission (mean range was 0.07 to 0.26) and when calculated for individual transmitters the medians showed even greater variation, ranging from 0.0 to 0.69 positions recorded per transmission. The site-level values for positioning efficiency were lower than other positioning efficiencies from VPS arrays reported in the literature. Roy et al. [19] found a mean efficiency of 0.40 after filtering positions with high estimated errors out of the dataset, and Espinoza et al. [16] reported an efficiency range of 0.28 to 0.53 positions recorded per transmission. Simpfendorfer et al. [26] examined the detection efficiency at single Vemco receivers, and reported a broad range of efficiency from 0.01 to 0.77 detections per transmission. While the overall positioning efficiencies reported here were at the lower limits of those reported in similar studies, they are reasonable considering the challenges of signal propagation at our study sites. These challenges at the coastal site included high noise interference from biological sources and stands of macroalgae, at the estuarine site they included patchy beds of freshwater macrophytes, and at the riverine site the greatest impediments were the complex hydrodynamics, entrained air, and noise from bedload movement. In addition to lost transmissions and those masked by environmental noise, there may have been additional loss of efficiency due to the collisions of concurrent transmitter signals. This can occur within a VPS array when there are high numbers of active transmitters. When we examined the potential for collisions at these sites we did not see a clear relationship between positioning efficiency and the number of transmitters and corresponding pulse rates (Table 3).
GLMM results indicated that the geometry of receivers in a positioning array was the most consistent factor affecting performance. For all analyses addressing HPEm, we saw that when viewing angles became more acute (that is, tags were farther from the internal area of the array) the error increased, which is in agreement with previous work on the spatial distributions of error in a positioning array [12, 18, 19]. However, when examining the positioning efficiency, two of the three models suggested that more acute angles resulted in increased efficiency. This result is surprising, and may be due to greater concentrations of transmitter signals closer to the center of the arrays, resulting in more transmitter collisions and reduced positioning efficiency as the viewing angle increases. Alternatively, the pattern may be spurious, resulting from unmeasured attributes that varied by specific transmitter location. These attributes could include elements such as localized vegetation, hydrodynamics, or softer substrates that may increase signal absorption. Because these factors vary in space but are are unrelated to the array geometry, they could lead to confounding results.
Five of the six final models included a metric for water movement, suggesting this is a common feature affecting positioning performance. Depending upon the habitat type, water movement was measured as wave behavior, tidal influence and flow, or river stage, all of which have the ability to move moored receivers and introduce error into recorded transmitter positions. This source of error is likely to be most extreme for non-rigid mooring systems. All the receivers tested here were attached to stainless steel cable, anchored using bottom weights and floated into a vertical position with small buoys. This mooring design allowed the receivers to move slightly within the water column. Among the three arrays tested, this movement was likely the most pronounced in the riverine array where the model predicted that a 0.5 m (1.7 ft) rise in stage, and accompanying increase in water velocity, should result in an additional 1.8 m of positioning error. Therefore careful attention should be paid to mooring designs in research areas that are likely to have high or variable currents. While the error due to receiver movement may be reduced through the use of more rigid mount designs, without a self-righting capability these designs pose an additional risk of the mounts becoming unintentionally fixed in a horizontal position. In addition to contributing to receiver movement, extremely strong flows such as those commonly encountered in riverine systems may also create an ‘acoustic wall’ along the region of fastest water movement. A subjective assessment of the transmitter detections in the riverine system indicated that very few detections were recorded across the thalweg, and this may have contributed to the low positioning efficiency.
The statistical models also suggest an interesting relationship between positioning performance and water temperature. In the models of HPEm, the coastal and estuarine sites show increased positioning error as water temperatures increased. We believe this is not due to effects of warmer water but rather be due to the use of mean water temperature estimates in the postprocessing positioning equations. User-defined parameters of temperature and salinity at the study site are used to estimate the speed of sound in the triangulation equations, and larger errors in these estimates lead to larger positioning errors. When we examined the difference between the actual water temperatures and the average temperatures assumed in the postprocessing positioning equations, we did in fact find larger differences at higher water temperatures, which may explain the results from the statistical models. Likewise, the model for HPEm at the estuarine site also included a positive relationship between positioning error and conductivity. A comparison of the measured variation in salinity and the average values used in the positioning equations suggest the same mechanism may have led to the positive conductivity relationship indicated in the model. For long study periods in habitats with variable temperature and/or salinity, system performance could be improved by estimating the speed of sound from water quality parameters measured more frequently than those used in these case studies.
At all three sites there was reasonable evidence for declining performance due to environmental noise. In the coastal array we saw decreased positioning efficiency at night, which has been noted in other marine applications of ultrasonic telemetry as well [4, 21]. Nocturnal organisms such as snapping shrimp can create sharp, loud noises that are difficult to discriminate from transmitter pulses [22] and can raise the variable noise threshold of receivers, making the transmission more difficult to detect (D. Webber, personal communication). The diel period was also an important factor at the estuarine array, but it showed the opposite relationship. The study site is a popular area for recreational fishing and boating, and it is likely that the increased motorized boating during daylight hours contributes high levels of background noise. It is also possible that sound waves from recreational sonar units (fish-finders) impede system performance during daytime periods (D. Webber, personal communication). Finally, at the riverine site we saw a strong relationship between river stage and both performance metrics. As discussed above, we expect the hydrodynamics at the site contributed to positioning errors through receiver movement. But we also noted that higher flows were related to reduced positioning efficiency, possibly because flow increases mobilized additional bedload. The collision of gravels and cobbles along the substrate can be clearly heard via mobile receivers, and it is plausible that high bedload movement can cause enough ambient noise to interfere with the reception of ultrasonic transmitters at greater discharges. In addition, turbulent flow patterns can entrain air into the water column, which can absorb an ultrasonic transmission and lead to reduced positioning efficiency [3].
Interestingly, final models for the estuarine array did not include the index for macrophytes, even though we anticipated that aquatic vegetation would absorb a substantial amount of any ultrasonic transmission passing through an existing patch. While a log-likelihood ratio test and AIC values indicated that the model without the macrophyte index was more parsimonious, the removal of this index during model selection only reduced the AIC value by 1.5, and did not cause any noticeable changes in parameter estimates for other variables. When we examined the model containing aquatic macrophytes both as a fixed effect and as a random slope by transmitter, we noted there were two transmitters that showed a strongly negative relationship with increasing macrophyte index (Figure 10). These two transmitters (B-02 and B-03; red and blue in Figure 10) were moored in substantially thicker beds of macrophytes during the peak growing season. This supports a hypothesis that aquatic vegetation may influence system performance at a smaller scale than the metrics used in this analysis.
Predicted relationships between positioning efficiency and macrophyte index at the estuarine site. Estimated overall relationship of macrophyte index (thick green line) as well as the divergent effects of each fixed transmitter (thin black lines) when macrophyte index was modeled with both random intercepts and random slopes. Two transmitters, B-02 and B-03, highlighted in red and blue, respectively, show much different trends than the remaining 11 tags. These two transmitters were located in denser macrophyte beds.
Conclusions
Based on the results of this analysis, it is clear that researchers planning to use an ultrasonic positioning system should carefully evaluate the appropriateness of such a system for each research question and environment [4]. Time should be invested in testing various receiver geometries, as this consistently appears as the most important predictor of performance. Careful consideration of methods to reduce receiver movement may also increase system performance. When research will be conducted at a site with variable temperature and salinity, water quality parameters should be monitored and utilized in postprocessing to reduce errors in the calculated positions. Finally, researchers should be prepared for moderate to high rates of data loss due to environmental noise. Even for the estuarine array, which performed best among those evaluated, on average only 28% of the expected transmitter pulses were converted into positions; the values for the coastal and riverine sites were even lower. Finally, while the environmental conditions examined here are common to many aquatic systems, this analysis did not include environments with thermoclines, nor environments affected by surface ice. It is important to note that each individual study area will present its own unique set of variables that researchers should consider on a case-by-case basis.
The ability to observe animal movement and habitat use in aquatic ecosystems can provide critical insight into basic ecological questions. Innovations in ultrasonic positioning systems have expanded our ability to conduct important research. Through sharing information on the performance abilities of these systems under real environmental challenges, we hope that future researchers will be able to design more effective positioning arrays and collect high quality information about the movement and behavior patterns of focal species.
Methods
Study sites
The three sites considered in this study encompass three broad aquatic habitats where ultrasonic telemetry is frequently utilized: oceans, estuaries, and rivers. At each site the positioning arrays differed in receiver density and coverage area due to constraints of the individual studies (Table 4). The coastal site was located on the coastal shelf off San Diego, California within the Point Loma kelp forest (Figure 2a). The Point Loma kelp forest is approximately 10 km long by 1 km wide, and dominated by giant kelp (Macrocystis pyrifora) and understory kelps (Pterygophora californica and Laminaria farlowii). The substrate consists of boulders on claystone bedrock, with shallow ledges undercutting the bottom. Areas of hard substrate with dense algal growth are interspersed with channels of sand supporting little to no algal growth. The positioning array was located approximately 1 km from shore (32.691°, -117.263°) at a depth of 12 to 14 m within the preferred habitat of the focal species, pink abalone (Haliotis corrugata). Algal growth was thick, including canopy of giant kelp resting at the surface. The mean tidal range was 1.13 m, salinity was relatively stable around 33 ppt, and surface temperature ranged from 13° to 22°C throughout the year. Because current velocities inside a large kelp bed are greatly reduced, much of the Point Loma kelp forest experiences velocities that are negligible to less than 5 cm s-1 [27]. Wind-generated surface waves can produce dramatic disturbances as they produce drag forces on surface canopy that can tear whole kelp plants from the substratum [28]. The area experiences intermittent boat traffic, predominantly from recreational fishers and divers.
The estuarine site was in a shallow tidal lagoon known as Mildred Island (37.975°, -121.530°) in the freshwater portion of the San Francisco Estuary, near the town of Stockton, California. Before 1983, this area was a deeply subsided agricultural island. The protective levees broke in 1983 and the flooded land was not reclaimed [29]. The resulting lake-like habitat is approximately 1.5 km wide and 3 km long, surrounded by overgrown levees with varying amounts of rock revetment. It has a fairly uniform depth of 4 to 5 m, soft substrates, a maximum tidal range of 1.2 m, and damped currents driven by both tidal and freshwater inputs [30]. Water temperatures generally range from 8° to 25°C over the course of the year. The study site was located in the SW corner of the flooded island, bounded on the northern and southern sides by levee revetment lined with beds of emergent California tule (Scirpus californicus). The shallow subtidal habitats of the northern shoreline were dominated by sand with sparse patches of submerged aquatic vegetation (SAV) while the subtidal habitats along the south-western shoreline were dominated by mud with dense beds of SAV. One of the two primary levee breaches in Mildred Island is located at the SE corner of the study site, which resulted in stronger currents along the eastern edge of the array. There is generally a moderate amount of boat traffic in the area from sport fishing and pleasure boats.
The riverine site was in the Sacramento River south of the town of Red Bluff, California. The study site was located just below the confluence of Antelope Creek (40.082°, -122.116°) at a deep hole known to be a spawning aggregation site for the focal species, green sturgeon (Acipenser medirostris). The river is approximately 120 m wide in the reach where the VPS was deployed, and has a variable depth profile reaching 11.5 m at the deepest point, with mean depths around 4.5 m. Under regulation from Shasta dam, the mean discharge is 330 m3 s-1 (1946 to 2009) [31]. During the study period cross-sectional surveys of the site recorded a mean discharge of 342 m3 s-1 and mean water velocities ranging from 0.425 m s-1 to 0.689 m s-1, with complex hydrodynamics and local velocities reaching more than 1.5 m s-1 (Thomas et al. unpublished observations). Water temperatures generally range from 6°C to 17°C over the course of the year. Most of the substrate in this reach is gravel and cobble, with areas of sand and areas of scoured bedrock. Both banks of the river are used for agriculture, with orchards on the east bank and grazing lands on the west.
Positioning array design
The initial design of each VPS positioning array was based on in-situ range tests to inform the optimal distances between receivers, and upon constraints due to geography of the local habitat and behavior of the study species. Each array used a variable number of VR2W receivers to detect transmitters operating at a frequency of 69 kHz, with an output power in the range of 147 to 156 dB re 1 μPa @ 1 m. Transmitters were programmed to emit a coded signal, and code bursts were sent at a set random interval (for example, 30 to 90 s) to reduce the chance that two transmitters would repeatedly collide with one another. Receivers were suspended on a stainless-steel cable approximately 1 to 2 m above the substrate and held vertically with foam floats. Time-synchronizing transmitters were moored at fixed locations within the study array, either co-located with receivers or placed at independent locations (Figure 2). These fixed transmitters were primarily intended to allow synchronization of the internal clocks of the independent VR2W receivers, but they also provided an opportunity to assess the performance of the array. The location of all receivers and fixed-location transmitters were recorded at each deployment using differentially corrected GPS technology. See Espinoza et al. [16] for additional details on deployment and data processing for a VPS.
Model variables
Two metrics were selected to compare the performance of each positioning array under varying environmental conditions: the horizontal positioning errors and the positioning efficiency. Each of these was estimated for fixed-location transmitters located within arrays. Horizontal positioning errors were calculated as the distance in meters between a VPS positioned location and the GPS location recorded for that transmitter. At the riverine site, strong currents resulted in one unexpected transmitter movement that required a new location to be derived from the VPS positioning data during postprocessing. This derived position was then used as the reference location for calculating subsequent horizontal positioning errors. Positioning efficiency was normalized for different transmitter programming by dividing the number of positions the VPS recorded by the expected number of transmissions over 12 h intervals.
Based on the intrinsic constraints of the VPS system and variation in aquatic acoustic conditions, we selected a set of variables to assess for relationships with system performance (Table 1). We considered the geometry of the array as an important user-defined factor for performance based on previous research [12, 16, 17, 19]. The spatial configuration of fixed transmitters and receivers was summarized with a ‘viewing angle’, defined by Berge et al. [18] and described above. Viewing angles were calculated using a geographic information system (ArcMap 10.1, ESRI Corporation, Redlands, CA, USA).
Environmental variables were obtained from publically available long-term monitoring programs (for example, Wave Rider Buoys and USGS monitoring stations). While this is not as preferable as direct measurements at a site, these sources do provide good estimates of the relative change in continuous water quality and weather parameters, as confirmed with temperature loggers installed at the estuarine site. To evaluate potential diel patterns in environmental noise we also included a two-level categorical variable. Transmitter detections between 19:00 and 7:00 were considered ‘night’ detections and those between 7:00 and 19:00 were considered ‘day’ detections.
At the coastal study site we used environmental data from the NOAA National Buoy Data Center [32] recorded at a buoy located approximately 11.9 km NW of the study site in water 200 m deep (Station 46231, Scripps Institute of Oceanography @ 32.748°, -117.370°). We used measurements summarized over 20 min sampling periods for water temperature (°C), average and dominant wave period (s), mean wave direction (degrees true), and significant wave height (m). The distribution of giant and understory kelps relative to tags and receivers was not measured during the study and these may have influenced performance. In particular, giant kelp has the greatest potential to block transmissions with gas bladders continuously positioned from the bottom to top of the water column. However, care was taken at the time of placement by divers on SCUBA to not place tags and receivers immediately next to algae to prevent entanglement.
At the estuarine study site we used environmental data from the USGS National Water Information System [33] recorded at a gauge located approximately 3.5 km downstream of the study site on the Middle San Joaquin River, near Holt, California (USGS gauge 11312685 @ 32.530°, -117.431°). We used measurements taken at 15 min intervals for water temperature (°C), electrical conductivity (μS/cm), and discharge (cfs) which was modeled in two parts: absolute discharge and a categorical variable indicating ebb or flood tide. Temperature measurements closely matched values collected by on-site data loggers. We excluded available variables that were tightly correlated with other selected metrics (river stage and velocity) as well as those that vary at small spatial scales within the estuary (chlorophyll and water turbidity) because we did not feel the measurements at the gauge would appropriately reflect conditions at the study site. In addition to variables from the USGS gauge, every 6 weeks we sampled the density of submerged aquatic vegetation at the estuarine site along set transects using a thatching rake. These measurements were converted into an index of overall macrophyte density to be included in our models.
At the riverine study site we used environmental data accessed from California Department of Water Resources’ California Data Exchange Center [34], recorded at a gauge located approximately 11.5 rkm upstream of the study site on the Sacramento River, near the Red Bluff Diversion Dam (USBR gauge @ 40.1544°, -122.2020°). We used hourly measurements of water temperature (°C), river stage (ft), and water turbidity (ntu). We excluded available measurements for dissolved oxygen because we did not feel the measurements at the gauge would reliably reflect conditions at the study site.
Data analysis
To assess performance of the VPS arrays, we constructed a general linear mixed model for each performance metric at each site. All potential explanatory variables were evaluated for collinearity within each model. Where there were high variance inflation factors, variables were selected for removal based upon the bivariate relationships between those variables in question and the performance metric. The variables with the strongest relationships were retained for the subsequent model selection process. In addition, because of the periodic nature of the sampling for macrophytes at the estuarine site, we reduced the full dataset of system performance to only 5 days surrounding each of the eight sampling periods. The resulting dataset included 40 days, evenly spaced throughout the deployment period. This created a sample size that was more comparable to the 60- and 49-day datasets analyzed from the coastal and riverine sites, respectively.
There were many positions with small horizontal positioning errors and few with large errors. Thus, to reduce the heterogeneity of variance in the model residuals, the measured horizontal positioning error (HPEm) was transformed with a ln(Y i + 1) transformation. The new response variable was modelled using a Gaussian linear mixed model. Based on the data structure we tested both transmitter ID and Julian date as random effects by evaluating all combinations of random effects using AIC values, following the procedure recommended by Zuur et al. [35]. To model positioning efficiency, we used a binomial general linear mixed model with a logit link function as appropriate for a proportional response variable. Both transmitter ID and Julian date were tested for inclusion as random effects. Because the explanatory variables were continuous and approximately normally distributed, they were summarized with mean values calculated over the same 12 h periods used to compute positioning efficiency. For the estuarine site we also considered a random intercept and slope for the macrophyte index, letting the slope vary by transmitter because macrophyte growth was the only variable which displayed substantial spatial variation. To select the final suite of fixed effects for each model, we used backwards step-wise selection based on AIC values and log-likelihood ratio tests [35]. Statistical analyses were performed in R [36], and mixed models were fit using the lme4 package [37].
References
Nathan R, Getz WM, Revilla E, Holyoak M, Kadmon R, Saltz D, Smouse PE: A movement ecology paradigm for unifying organismal movement research. Proc Natl Acad Sci U S A 2008, 105: 19052–19059. 10.1073/pnas.0800375105
Lucas MC, Baras E: Methods for stuyding spatial behavoir of freshwater fishes in the natural environment. Fish Fish 2000, 1: 283–316. 10.1046/j.1467-2979.2000.00028.x
Cooke SJ, Midwood JD, Thiem JD, Klimley AP, Lucas MC, Thorstad EB, Eiler J, Holbrook C, Ebner BC: Tracking animals in freshwater with electronic tags: past, present and future. Anim Biotelem 2013, 1: 1–5. 10.1186/2050-3385-1-1
Heupel MR, Semmens JM, Hobday AJ: Automated acoustic tracking of aquatic animals: scales, design, and deployment of listening station arrays. Mar Fresh Re 2006, 57: 1–13. 10.1071/MF05091
Klimley AP, Voegeli F, Beavers SC, Le Boeuf BJ: Automated listening stations for tagged marine fishes. Mar Technol Soc J 1998, 32: 94–101.
Klimley AP, Holloway C: Homing synchronicity and schooling fidelity by yellowfin tuna. Mar Biol 1999, 133: 307–317. 10.1007/s002270050469
Cooke SJ, Hinch SG, Wikelski M, Andrews RD, Kuchel LJ, Wolcott TG, Butler PJ: Biotelemetry: a mechanistic approach to ecology. Trends Ecol Evol 2004, 19: 334–343. 10.1016/j.tree.2004.04.003
Klimley AP, Le Boeuf BJ, Cantara KM, Richert JE, Davis SF, Van Sommeran S, Kelly JT: The hunting strategy of white sharks ( carcharodon carcharias ) near a seal colony. Mar Biol 2001, 138: 617–636. 10.1007/s002270000489
Whitney NM, Pratt HL Jr, Pratt TC, Carrier JC: Identifying shark mating behavior using three-dimensional acceleration loggers. Endang Species Res 2010, 10: 71–82.
Clark DS, Green JM: Activity and movement patterns of juvenile Atlantic cod, gadus morhua , in conception Bay, Newfoundland, as determined by sonic telemetry. Can J Zoolog 1990, 68: 1434–1442. 10.1139/z90-214
O’Dor RK, Andrade Y, Webber DM, Sauer WHH, Roberts MJ, Smale MJ, Voegeli FM: Applications and performance of radio-acoustic positioning and telemetry (RAPT) systems. Hydrobiologia 1998, 371: 1–8.
Klimley A, Le Boeuf B, Cantara K, Richert J, Davis S, Van Sommeran S: Radio acoustic positioning as a tool for studying site-specific behavior of the white shark and other large marine species. Mar Biol 2001, 138: 429–446. 10.1007/s002270000394
Voegeli FA, Smale MJ, Webber DM, Andrade Y, O’Dor RK: Ultrasonic telemetry tracking and automated monitoring technology for sharks. Environ Biol Fish 2001, 60: 267–281. 10.1023/A:1007682304720
Watkins WA, Schevill WE: Sound source location by arrival-times on a non-rigid three-dimensional hydrophone array. Deep-Sea Res 1972, 19: 691–706.
Andrews KS, Tolimieri N, Williams GD, Samhouri JF, Harvey CJ, Levin PS: Comparison of fine-scale acoustic monitoring systems using home range size of a demersal fish. Mar Biol 2011, 158: 2377–2387. 10.1007/s00227-011-1724-5
Espinoza M, Farrugia TJ, Webber DM, Smith F, Lowe CG: Testing a new acoustic telemetry technique to quantify long-term, fine-scale movements of aquatic animals. Fish Res 2011, 108: 364–371. 10.1016/j.fishres.2011.01.011
Smith GW, Urquhart GG, Maclennan DN, Sarno B: A comparison of theoretical estimates of the errors associated with ultrasonic tracking using a fixed hydrophone array and field measurements. Hydrobiologia 1998, 372: 9–17.
Berge J, Capra H, Pella H, Steig T, Ovidio M, Bultel E, Lamouroux N: Probability of detection and positioning error of a hydro acoustic telemetry system in a fast-flowing river: intrinsic and environmental determinants. Fish Res 2012, 125: 1–13.
Roy R, Beguin J, Argillier C, Tissot L, Smith F, Smedbol S, De-Oliveira E: Testing the VEMCO positioning system: spatial distribution of the probability of location and the positioning error in a reservoir. Anim Biotelem 2014, 2: 1–6. 10.1186/2050-3385-2-1
Nelson DR: Telemetering techniques for the study of free-ranging sharks. In Sensory Biology of Sharks, Skates, and Rays. Edited by: Hodgson ES, Mathewson RF. Arlington, VA: Office of Naval Research, Dept of the Navy; 1978:419–482.
Payne NL, Gillanders BM, Webber DM, Semmens JM: Interpreting diel activity patterns from acoustic telemetry: the need for controls. Mar Ecol Prog Ser 2010, 410: 295–301.
Fish MP: Biological sources of sustained ambient sea noise. In Marine bio-Acoustics. Edited by: Tavolga WN. New York, NY: Pergamon Press; 1964:175–194.
Coates JH, Hovel KA, Butler JL, Klimley AP, Morgan SG: Movement and home range of pink abalone haliotis corrugata : implications for restoration and population recovery. Mar Ecol Prog Ser 2013, 486: 189–201.
Guisan A, Zimmermann NE: Predictive habitat distribution models in ecology. Ecol Model 2000, 135: 147–186. 10.1016/S0304-3800(00)00354-9
Meckley TD, Holbrook CM, Wagner CM, Binder TR: An approach for filtering hyperbolically positioned underwater acoustic telemetry data with position precision estimates. Anim Biotelem 2014, 2: 7. 10.1186/2050-3385-2-7
Simpfendorfer CA, Heupel MR, Collins AB: Variation in the performance of acoustic receivers and its implications on positioning algorithms in a riverine setting. Can J Fish Aquat Sci 2008, 65: 482–492. 10.1139/f07-180
Jackson GA: Currents in the high drag environment of a coastal kelp stand off California. Cont Shelf Res 1997, 17: 1913–1928. 10.1016/S0278-4343(97)00054-X
Dayton PK, Tegner MJ, Edwards PB, Riser KL: Sliding baselines, ghosts, and reduced expectations in kelp forest communities. Ecol Appl 1998, 8: 309–322. 10.1890/1051-0761(1998)008[0309:SBGARE]2.0.CO;2
Lopez CB, Cloern JE, Schraga TS, Little AJ, Lucas LV, Thompson JK, Burau JR: Ecological values of shallow-water habitats: implications for the restoration of disturbed ecosystems. Ecosystems 2006, 9: 422–440. 10.1007/s10021-005-0113-7
Monsen NE, Cloern JE, Lucas LV, Monismith SG: A comment on the use of flushing time, residence time, and Age as transport time scales. Limnol Oceanogr 2002, 47: 1545–1553. 10.4319/lo.2002.47.5.1545
Report W-D: 11389500 Sacramento River at Colusa, CA. US Geological Survey: Department of the Interior; 2009. [http://wdr.water.usgs.gov/wy2013/pdfs/11389500.2013.pdf]
NOAA national buoy data center [http://www.ndbc.noaa.gov]
USGS national water information system [http://waterdata.usgs.gov/nwis]
California department of water resources’ California data exchange center [http://cdec.water.ca.gov]
Zuur AF, Ieno EN, Walker N, Saveliev AA, Smith GM: Mixed Effects Models and Extensions in Ecology With R. New York, NY: Springer; 2009.
R core team: R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing; 2013. [http://www.R-project.org]
Bates D, Maechler M, Bolker B, Walker S: lme4: linear mixed-effects models using eigen and S4. 2013.
Acknowledgements
The authors would like to thank the numerous people who provided vital field support, including Michael Thomas, Phillip Sandstrom, Gabriel Singer, Dennis Cocherell, Eric Chapman, Ryan Battleson, and Cynthia Catton. Many thanks to Dale Webber, Kevin A. Hovel, John L. Butler, Steven G. Morgan, and Megan Wyman who provided intellectual and/or financial support. Thanks also to two anonymous referees who provided constructive feedback. The coastal ocean study was funded by the NOAA Species of Concern Program and the Joint Doctoral Program in Ecology at San Diego State University and University of California, Davis. The estuarine study was funded by the Interagency Ecological Program, the University of California, Davis, and the National Science Foundation under Grant No. 0841297. The riverine study was funded by the US Bureau of Reclamation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AES performed field work, conducted the initial processing of array positions, completed the analyses, and wrote drafts of the manuscript. JC and AH each performed field work, conducted the initial processing of array positions, and provided insight to their respective study systems as well as comments on manuscript drafts. APK provided guidance in the initial study formulation, as well as assistance with manuscript preparation. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Steel, A.E., Coates, J.H., Hearn, A.R. et al. Performance of an ultrasonic telemetry positioning system under varied environmental conditions. Anim Biotelemetry 2, 15 (2014). https://doi.org/10.1186/2050-3385-2-15
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2050-3385-2-15