Abstract
The seismic vulnerability of highway bridges remains an important problem and has received increased attention as a consequence of unprecedented damage observed during several major earthquakes. A significant number of research studies have examined the performance of skew bridges under service and seismic loads. The results of these studies are particularly sensitive to modeling assumptions in view of the interacting parameters. In the present study, three-dimensional improved beam-stick models of two-span highway bridges with skew angles varying from 0° to 60° are developed to investigate the seismic response characteristics of skew box girder bridges. The relative accuracy of beam-stick models is verified against counterpart finite element models. The effect of various parameters and conditions on the overall seismic response was examined such as skew angle, ground motion intensity, soil condition, abutment support conditions, bridge aspect ratio, and foundation-base conditions. The study shows that the improved beam-stick models can be used to conduct accurate nonlinear time history analysis of skew bridges. Skew angle and interacting parameters were found to have significant effect on the behavior of skewed highway bridges. Furthermore, the performance of shear keys may have a predominant effect on the overall seismic response of the skew bridges.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Design codes and guidelines for static and dynamic analyses of regular bridges are well-established and understood. However, there remains significant uncertainty with regard to the response characteristics of skew highway bridges as it is reflected by the lack of detailed procedures in the current guidelines. As evidenced by past seismic events (e.g., 1994 Northridge - Gavin Canyon Undercrossing and 1971 San Fernando - Foothill Boulevard Undercrossing), skew highway bridges are particularly vulnerable to severe damage due to earthquakes. Even though a number of studies have been conducted over the last three decades, research findings have not been sufficiently comprehensive to address the response characteristics of skew highway bridges under static and dynamic loading. Therefore, a large number of highway bridges are still at risk with consequential threat to loss of function, life safety, and economy following a major earthquake.
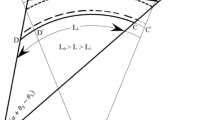
AASHTO (2011) stated that two-dimensional model is sufficient for bridges with skew angle less than 30°; however, for bridges with larger skew angles, three-dimensional (3D) models that account for the skew angle are necessary. It is generally agreed that bridges with skew angles greater than 20° exhibit complex response characteristics under seismic loads. Saiidi and Orie (1992) noted the skew effects and suggested that simplified models and methods of analysis would result in sufficiently accurate predictions of seismic response for bridges with skew angles less than 15°. On the other hand, Maleki (2002) concluded that slab-on-girder bridges with skew angles up to 30° and spans up to 20 m have comparable response characteristics to straight bridges, and therefore, simplified modeling techniques such as rigid deck modeling were justified in many cases. Bjornsson et al. (1997) conducted an extensive parametric study of two-span skew bridges modeled with rigid deck assumption. In this study, the maximum relative abutment displacement was found to be influenced strongly by the impact between the deck and the abutments. A critical skew angle was introduced as a function of span length and width that maximizes the rotational impulse due to impact, and it was found to be between 45° and 60°.
In comparing results across various analytical studies, one must consider the underlying assumptions implemented in the analytical treatment of the skew highway bridges. These may pertain to material modeling, inelastic (hysteretic) response characteristics of the components, boundary conditions, soil-structure interaction, component modeling (i.e., idealized beam-stick vs. finite element), superstructure (i.e., rigid vs. flexible), seismic mass (i.e., distributed vs. lumped), etc. For instance, Meng and Lui (2000) suggested that the effects of modeling boundary conditions properly may outweigh the effects of skew angle on the overall dynamic response characteristics of a bridge. In fact, differences in assumptions may lead to inconsistent results as seen in the analysis of the Foothill Boulevard Undercrossing, which sustained severe damage during the San Fernando earthquake. A study conducted by Wakefield et al. (1991) concluded that the failure was controlled by rigid-body motion, which agreed with study conducted by Maragakis (1984). On the other hand, a study conducted by Ghobarah and Tso (1974) explained that highway bridges are sensitive to damage due to earthquake when located near faults. Ghobarah and Tso (1974) assumed the deck was fixed at the abutments, while Wakefield et al. (1991) assumed free translation of the deck at the abutments. Meng et al. (2001) concluded that the response of skew bridges depends on the deck aspect ratio, stiffness eccentricity ratio, skew angle, natural frequency, and frequency ratio. Meng and Lui (2002) introduced and validated an accurate dual beam stick modeling technique for skew bridges. The present study utilizes this approach and introduces further improvements.
The present study introduces an improved, simplified modeling technique generally applicable for box girder bridges. Subsequently, results of a comprehensive investigation on the effect of some of the interacting parameters and conditions with the skew angle, namely, ground motion intensity, soil type, abutment support conditions with nonlinear soil interaction and shear keys, bridge aspect ratio, and foundation base conditions, are reported.
Methods
Benchmark bridge
A total of twelve reinforced-concrete box girder bridges located in California were considered in establishing the geometry and properties of a so-called benchmark bridge. The average properties were best represented by bridge 42-0427 L/R and it was selected for further analytical investigation. Hence, the benchmark bridge is a two-span concrete box girder bridge with a span length of 40.85 m. In addition, the selected bridge has the largest skew angle of 52° among the 12 bridges with an aspect ratio of approximately 0.3. The aspect ratio is defined as the ratio of the width (including the overhang) to the span length of the bridge. Figure 1 shows the cross section of the benchmark bridge. Subsequently, the benchmark bridge model was altered to develop models with various skew angles and aspect ratios (Figures 2 and 3) as discussed in what follows.
Modeling of bridges
In order to facilitate a comprehensive analytical study, improved 3D beam-stick models of the bridges were developed (Figure 4). Significant effort was necessary to arrive at consistent inelastic modeling assumptions for various structural details as will be discussed later. Attention was given to ensure that the models were general enough to capture the global response characteristics and, at the same time, detailed enough to allow accurate estimation of component level seismic response, both in elastic and inelastic ranges.
In the light of these objectives, both 3D finite element (FE) and improved 3D beam-stick (BS) models of some of the selected bridge geometries were developed. SAP2000 Computers and Structures, Inc. (2005) was used to develop detailed nonlinear 3D FE as well as improved BS models, whereas DRAIN3DX Prakash et al. (1994) was employed to develop the improved BS models only. The superstructure was assumed to be linear elastic, and all of the nonlinearity was assumed to take place in the substructure elements, including bents, shear keys, pounding, and abutment-soil interaction. In order to ensure and assess the accuracy of the simplified models (BSs), different models (FE and BSs) of the same bridge geometries were subjected to the same excitation and results were compared in terms of both global and component level response. As it will be further demonstrated, improved 3D BS models were deemed sufficiently accurate and efficient compared to their 3D FE counterparts. Also, the analysis time was reduced by approximately 70% and that is deemed necessary to efficient fragility studies. Models of the bridges with three different aspect ratios have been developed as shown in Figures 123. Table 1 summarizes the properties of superstructure, bent cap beam, and bent columns for these bridges. It is noted that the span length of 40.85 m was kept constant while the deck width was increased to achieve aspect ratios of 0.3, 0.54, and 1.1.
Finite element models: SAP2000
The models under study have skew angles: 0°, 20°, 30°, 45°, 52° (benchmark), and 60°. The benchmark bridge is a two-span bridge with a two-column interior bent, with bent caps and end diaphragms at the abutments. For each skew, a finite element mesh was used to model the deck, soffit, girders, and diaphragms. The internal bent cap and end diaphragms at the abutments were modeled explicitly as part of the superstructure. The nodes making up each diaphragm were constrained so that the joints move together as a diaphragm that is rigid against membrane deformations. It should be mentioned that each diaphragm and bent is aligned along the skew angle. The bent columns and footings were modeled using 3D beam-column elements (Figure 1) whose properties are summarized in Table 1. The nonlinearity was assumed to take place in columns, shear keys, pounding, and abutment-soil interaction. Plastic hinge properties were assigned and located at the top and bottom of the columns; the fiber P-M2-M3 (PMM)-type hinge was used to model the plasticity in columns. However, it was found necessary to conduct a parametric study to establish accurate parameters to define fiber hinges including the proper number of fibers, plastic hinge length, and plastic hinge location with respect to the height of the bent columns. The footing was assumed to present either a pinned or fixed condition. The bearing links were assigned in the longitudinal and the transverse direction of the bridges. Nonlinear hysteretic response of shear keys, abutment-soil interaction, and pounding was modeled using various nonlinear springs arranged in series and/or parallel. This was necessary due to the absence of a single element with suitable hysteretic properties to model such behavior in SAP2000. However, the so-called ‘type 09’ element in DRAIN3DX allows direct explicit modeling of compression-only gap opening behavior to represent the response due to abutment-soil interaction, pounding, and the shear keys.
Accordingly, pounding is assumed to take place when the initial gap was closed. The gap element used for this purpose was assigned a ‘pounding stiffness’ consistent with the contact element formulation proposed by Muthukumar (2003) and also adopted by various researchers (e.g., Shamsabadi 2007; ElGawady et al. 2009) for an assumed penetration of 25 mm. The bridge deck is free to move in the longitudinal direction until the gap between the deck and abutment backwall is closed and hence soil stiffness will be activated. The properties of the abutment-soil interaction springs were calculated using the backbone curve of the force displacement relationship of the soil. The backbone p-y relation for passive pressure at the abutment backwall was obtained from Caltrans Seismic Design Criteria Caltrans (2006, Section 7.8). The following equations are used to determine the stiffness at abutments (Kabt). It is important to note that the behavior is assumed to be elastic perfectly plastic.
where k i is the initial embankment fill stiffness which is 11.5 kN/mm/m, w is the width of the backwall, and h is the abutment height. The initial embankment stiffness was adjusted based on the height proportional factor. It is noted that the passive pressure increases linearly with the displacement. The maximum passive pressure is 239 kPa at displacement of 35 mm. beyond this point, the passive pressure levels out. This compression-only hysteretic response was modeled with a series arrangement of two elements (gap link element and elasto-plastic link element) as depicted in Figure 5. It was possible to achieve accurately the desired response characteristics in SAP2000. Abutment-soil springs that account for possible pounding were placed at the top and bottom of the deck at each girder in the FE models and similarly at the location of girders in the BS models.
The properties of the four external shear keys were determined based on the study by Megally et al. (2002). In general, shear keys are designed to provide resistance in the transverse direction of bridges, and their capacity is limited by the lateral capacity of piles. Similarly, since there is no single element in SAP2000 that can be used to model the hysteretic behavior of shear keys, a series and parallel arrangement of various nonlinear link elements is used. A multilinear elastic link element and multilinear plastic link element were connected in parallel and attached to a gap link element to simulate the hysteretic behavior of shear keys.
Beam-stick models: SAP2000
The beam-stick models were developed based on a refined stick model proposed by Meng and Lui (2002). The refined approach was introduced particularly for the modeling of highway bridges with relatively large skew angles and to capture dynamic response characteristics (coupling) more accurately, since the superstructure is modeled with two lines of girder elements. Obviously, the more the number of lines of girders, the more accurate simulations can be achieved. In the present study, a minimum of three lines of girder elements were found to better represent the distributed nature of the seismic mass and geometry of the superstructure (Figure 4) following the comparison to FE models. The equations below are general enough to the extent that they can be used to generate the properties of any number of lines of girders used. Hence, in the present study, three lines of girder elements were used to model bridges with aspect ratios of 0.3 and 0.54, while four lines of girder elements was found to be necessary for bridges with aspect ratio of 1.1. The properties of each beam stick (Table 1) were calculated using Equations 2, 3, 4, 5, and 6. It is important to note that the selection of the spacing between sticks can be determined using the condition that the mass moment of inertia of the actual deck in Equation 4 is equal to that of the stick model in Equation 6.
For the actual deck of the bridge,
For the beam-stick model,
where As is cross-sectional area of each stick, n is number of stick beams, Isy is moment of inertia of each stick about the Y-axis, Wm is tributary width of each stick, WT is total width of the deck, Iy is moment of inertia about the weak axis, Imz is mass moment of inertia of the bridge deck about the vertical axis, M i is mass of top/bottom flange of the bridge deck, L is span length, W i is width of top/bottom flange of the bridge deck, Θ is the skew angle, M j is the mass of the j th web, d j is perpendicular distance between the j th girder and the centerline of the deck, Iz is moment of inertia about the strong axis, Isz is moment of inertia of each stick about the Z-axis, S is spacing between stick beams, and Ms is mass of one stick. Note that x, y, and z axes are defined as longitudinal, transverse, and vertical axes respectively.
Figure 1 presents the bent elevation of the benchmark bridge with the aspect ratio of 0.3. The interior bent cap beam and the end diaphragms were modeled using 3D frame elements with large moment of inertia. The group of nonlinear link elements that represent the abutment-soil interaction and pounding was attached to the end diaphragms. The properties of nonlinear link elements, columns, and column PMM hinges were the same as those used in the FE models.
Beam-stick models: DRAIN3DX
In DRAIN3DX, compression-only hysteretic behavior can be modeled using a single element. The compression-only element (type 09) available in DRAIN3DX was employed to accurately model the hysteretic behavior of shear key, pounding, and abutment-soil interaction. An initial gap can be assigned to this element, and the assigned stiffness will not be active unless the developed gap (if any) is overcome at each time step during the time-history analysis. Instead of using fiber hinge assigned at particular locations, the element with a distributed plasticity (type 15) in DRAIN3DX was employed to model the nonlinearity in columns. This element can be used to model steel, reinforced concrete, and composite steel-concrete beams and columns. The element is divided into multiple segments. Each segment may be assigned a different cross section, and each cross section is made up of various fiber elements that may correspond to the longitudinal steel, concrete, etc. Each fiber element, hence, is assigned its associated nonlinear stress–strain properties. The cross-sectional properties were assumed to be the same throughout the individual segments. Later, a comparison to verify the accuracy of the use of this model will be presented.
Parametric study
Nonlinear models of the benchmark bridge was further refined and updated following a detailed parametric study. The primary purpose of the parametric study was to arrive at proper modeling techniques and assumptions to represent nonlinear response characteristics of bent columns, pounding, abutment-soil interaction, and shear keys to enable accurate and reliable system response prediction and assessment. Various modeling alternatives in both SAP2000 and DRAIN3DX were investigated and calibrated using some of the available experimental data. Also, a preliminary comparative nonlinear time history analysis was conducted to ensure the accuracy of beam-stick models developed in either SAP2000 or DRAIN3DX.
Modeling of the bent columns
There are several parameters that may affect the modeling of hysteretic response characteristics of bent columns. Depending on the software and the type of elements used, these parameters may be (1) number of fibers, (2) distribution of fibers on the cross section, and (3) plastic hinge definitions: length and location. The effect of these parameters was investigated by comparing analysis results with experimental responses from various component tests published in the literature Esmaeily and Xiao (2002; Saatcioglu and Baingo 1999; Cheok and Stone 1990). Various fiber distributions on the cross section were considered (e.g., Figure 6). For example, the entire cross section was divided into 12 identical wedges (12 fibers); each of the inner and outer cores of the cross section was divided into 12 identical wedges (24 fibers); finally, concrete fibers surrounding the location of reinforcements were introduced hence, the cross section was divided into 12 identical wedges to model the core and another 12 identical wedges to surround the reinforcement (24 fibers at reinforcement). The reinforcement was modeled by eight lumped steel fibers regardless of the actual distribution. The pushover analyses on the models of the columns were performed to simulate the different types of loading conditions on specimens. Figure 7 shows a representative comparison along with the relative error between analyses and experimental observations in Table 2. Based on this investigation, fiber distribution (Figure 6) in which concrete fibers surrounded the location of reinforcement (option c; 24 fibers at reinforcement) led to the most accurate results and therefore, it was recommended and used in the remaining of this study.
Comparison of analytical and experimental results: N6 Cheok and Stone (1990).
In addition, an investigation was carried out using a total of 45 different bent and column geometries to study the effect of the number of fiber sections (along the bent column length), plastic hinge locations, and lengths in DRAIN3DX and SAP2000. It was recommended that the column should be divided into a number of fibers which satisfy the condition that the fiber section length is at least 10% of the column height. The use of this condition in DRAIN3DX was sufficiently accurate to capture the nature of distributed plasticity, and a plastic hinge length of 10% of the column length was confirmed in SAP2000 as well.
Abutment-soil interaction
Skew bridge abutments, foundations, and surrounding soil constitute a strongly coupled system, and the dynamic behavior of a skew bridge structure and the abutment-soil interaction has been identified as having the first-order influence on dynamic response of the bridge Shamsabadi et al. (2004). It was suggested based on past experiences that even though the bridge structure during a seismic event could remain linear, the nonlinear abutment-soil interaction can lead to significant system nonlinearity. Therefore, it is recommended that for the realistic system response prediction, the abutment-soil interaction is included in the bridge response studies. In SAP2000 models, pounding and nonlinear abutment-soil response are modeled using a combination of springs as shown in Figure 5. The nonlinear gap element ensures that no pressure is applied to the abutment wall during a reversal, whereas the nonlinear elasto-plastic spring constitutes the soil properties (with optional post yield stiffness). Further refinement to this modeling approach is possible by introducing dashpot elements to model damping associated with soil response.
Shear keys
An earlier analytical study Abdel-Mohti and Pekcan (2008) has shown that the effectiveness of the internal shear keys in providing lateral capacity is affected significantly by the skew angle and may significantly affect the response characteristics of the bridge in general. For this reason, it was decided that an explicit modeling of the nonlinear shear key response is critical for the reliable and accurate assessment of the overall seismic response of skew highway bridges. Megally et al. (2002) studied experimentally cyclic pushover response of both internal and external shear keys. Capacity determination of external shear keys presented in that study has been adopted, and nonlinear external shear key response is modeled using a combination of link elements as shown in Figure 8 to simulate the entire hysteretic response using SAP2000. Experimental cyclic pushover response of a shear key is compared to that of analytical prediction in Figure 8 Megally et al. (2002).
Comparison of analytical and experimental response of external shear key Megally et al. ( 2002 ).
Preliminary comparative time history analysis
In order to measure the accuracy of BS models against the counterpart FE models, 1940 El Centro S00E record (scaled to PGA of 0.6 g) was used in a series of preliminary time-history analyses. A nonlinear static analysis including both dead load and post-tensioning preceded the time-history analyses. As can be seen in Figure 9, a good agreement between the various models was achieved. Further details of this preliminary investigation can be found in Abdel-Mohti (2009).
Seismic response of skew bridges
A wide range of parameters and their effects on the seismic response of bridges with various skew angles were investigated. As the accuracy of the improved BS models was established (Figure 9), subsequent investigation was conducted using DRAIN3DX. The effects of the following parameters on the seismic performance of the skew bridges were investigated: (1) skew angle (0° to 60°); (2) ground motion intensity (0.3 to 0.6 g); (3) soil type (B and D); (4) abutment support conditions including pounding, abutment-soil interaction, and shear keys (it is noted that all of the models included spring elements to model pounding, abutment-soil interaction, and shear key hysteretic response explicitly, unless otherwise noted); (5) bridge aspect ratio (0.3, 0.54, 1.1); and (6) foundation boundary conditions (fixed, pinned).
Selection of ground motions
The benchmark bridge (52° skew) was designed according to site-specific response spectra for soil type-D with moment magnitude, MW of 6.5 and peak ground acceleration (PGA) of 0.3 g. Two soil types (D and B), two PGA levels (0.3 and 0.6 g), and six ground motions for each of the PGA levels were selected. The acceleration time histories were obtained from PEER Strong Motion Database (2000) (http://peer.berkeley.edu/smcat) for epicentral distances of up to 30 km. The average acceleration spectra of the weaker and stronger components are compared to the Caltrans design acceleration response spectra (ARS) in Figure 10 for soil D. The stronger component of each ground motion is applied in the transverse direction of the bridge models, while the weaker component is applied in the longitudinal direction. It is noted that no significant effect of the orientation of excitation with respect to the skew angle is expected. The ground motions selected for soil type D are El Centro 1940, El Centro 1979, Loma Prieta 1989, Northridge 1994, Superstition Hills 1987, and Kocaeli Turkey 1999; and El Centro (Bond Corner) 1979, Duzce Turkey 1999, El Centro (Array no. 5) 1979, Loma Prieta 1989, Northridge (New Hall) 1994, and Northridge (Sylmar) 1994. Similarly, the ground motions selected for soil type B are Castaic 1971, Duzce Turkey 1999, Lake Hughes 1971, Loma Prieta 1989, Morgan Hill 1984, and Tabas Iran 1978; and Coalinga 1983, Duzce Turkey 1999, Kobe 1995, Loma Prieta 1989, Northridge (Castaic) 1994, and Northridge (Katherine) 1994, respectively.
Response parameters
Bridge models with skew angles 0°, 20°, 30°, 45°, 52°, and 60° were subjected to a total of 12 pairs of ground motions; 6 pairs with scaled PGAs of 0.3 g; and another 6 pairs with scaled PGAs of 0.6 g for each soil type B and D. All of the models have pinned bent foundations with abutment-soil interaction and shear keys modeled explicitly unless otherwise noted (Table 3). Several response parameters are monitored and reported with respect to the skew angle: (1) displacement in the longitudinal (U x ) and the transverse (U y ) directions at three nodes: 90 (at the bent), 74 (at 40% of the bridge span), and 64 (at the abutment) as shown in Figure 4; node 74 was selected at 40% of the bridge span in order to represent the displacement response of the bridge in the span of the bridge as well; (2) bending moment about the axes parallel to skew (M yy ) and normal to skew (M zz ), axial force, shear forces in axes parallel to skew (qy) and normal to skew (qz), and the maximum curvature ductility (μmax) for bent columns C1 and C2; (3) abutment-soil interaction (ug); and (4) shear key response (Usk).
Results and discussion
Effect of ground motion intensity and soil type
In order to investigate the effect of ground motion intensity and soil type on the seismic performance of skew highway bridges, nonlinear time history analyses were conducted on the bridge models using the two sets of ground motions with two levels of intensity (0.3 and 0.6 g) and for soil types B and D. Figures 11,12,13 present response comparison for deck longitudinal (U x ) and transverse (U y ) displacements and shear key deformation (Usk). The response of bridges in terms of column forces, abutment deformations, and maximum curvature ductility (μmax) was investigated and only discussed in what follows. μmax is the envelope of the average curvature ductility demand with respect to the skew angle in both directions (μ yy and μ zz ).
Figures 11 and 12 present the displacement of the deck in the longitudinal and transverse directions (x and y) respectively. In the longitudinal direction (Figure 11), the same trend was observed for the two levels of ground motions. As the skew angle increases, the displacement also increases since the longitudinal stiffness of the bridge reduces with increasing skew angle. It should also be noted that since the pounding and abutment-soil interaction springs are oriented normal to skew, their contribution in the longitudinal stiffness of the bridge tends to reduce with increasing the skew angle. The three nodes on the deck translated together with almost the same displacement longitudinally for the same skew angle which suggests that the deck behaves as a rigid body in the longitudinal direction. Also, the longitudinal displacement of the deck due to the application of ground motions with PGA of 0.6 g followed the same trend and was more than twice that due to the application of ground motions with PGA of 0.3 g. From Figure 11, it can be also concluded that the larger response was experienced by bridges on soil type D than those on soil type B by a factor about 1.5 for 0.6 g. This can be attributed to the fact that soil type D is softer which may magnify the response quantities.
In the transverse direction (Figure 12), insignificant variation was observed for nodes 90 and 74, while the displacement of node 64 (at abutment) which increased with skew angles, however, is small. The small transverse displacement at the abutment can be attributed to the presence of shear keys and the gap opening and closing of abutment springs. Transverse deck displacement due to the application of ground motions with PGA of 0.6 g was approximately twice than the application of ground motions with PGA of 0.3 g. It can be observed that the transverse displacement of the bridge deck is small at the abutment and increases towards the bent causing the bridge deck to bend in its plane in the transverse direction. This observation was valid for both soil types.
The moment developed in the columns due to the application of larger level of intensity was about two times higher than due to the application of the lower level intensity. M zz increases as the skew angle increases. This could be owing to the M zz affected by the presence of the shear keys which are designed to support the bridge in the transverse direction. No significant variation was reported for axial force in column with skew. The shear forces in columns in both directions (q y and q z ) showed similar trend to the moments in columns. The shear forces remained consistently below the calculated shear capacity for all skew angles Abdel-Mohti (2009). Another factor which can clearly show the effect of ground motion intensity is μmax. The calculated ductility factors were larger than unity which confirms that both columns yielded under 0.6 g level of ground motions while they remained elastic under 0.3 g for the bridge on soil type D. No yielding was observed in columns of bridges on soil type B. Also, there is a factor of more than 4 between the two levels of motions. However, it is interesting to note that the maximum ductility demand remains relatively constant for all skew angles. There has lower demand on columns on soil type B. All four abutment springs on one side of the bridge show similar trend for both soil types. There is a factor of 2 to 3 due to the application of larger level of intensity. As the skew angle increases, the displacement decreases. This suggests that the presence of shear keys may reduce the demand on abutment-soil interaction springs for larger skew angles, and failure of the shear keys may lead to a different trend particularly when the yielding of those springs may take place. It should be also mentioned that larger values were recorded for the abutment-soil interaction in bridges on soil type D.
Each bridge model has four external shear keys, one at each corner of the bridge as per Figure 4. Figure 13 presents the shear key deformations as a function of the skew angle. It can be observed that shear keys on the diagonals show similar trend. This observation is not pronounced for 0.3 g, but it becomes obvious for 0.6 g. The trend due to 0.6 g intensity level was different from that of 0.3 g intensity due to the yielding of the shear keys during the larger intensity motions for both types of soil. The increase in the level of intensity led to larger deformations in shear keys regardless of soil type. Also, under PGA of 0.3 g, it can be observed that shear key deformations are larger at the acute corner and tend to decrease towards the obtuse corner for most of the skew angles. Note that the effectiveness of the shear keys becomes less as skew angle increases. For PGA of 0.6 g, shear keys yielded and also, soil springs received higher demand.
Increasing the level of ground motion intensity led to larger response. Soil type does not have any significant effect on the trend of observed responses. Bridges on soil type-B showed smaller response values for all parameters compared to those on soil type D. Abutment-soil interaction springs and shear keys yielded for both soil types when subjected to ground motions with PGAs of 0.6 g. The effectiveness of the shear keys decreases as the skew angle increases. Consequently, the demand on shear keys increases with the skew. No yielding took place in columns of the bridge on soil B.
Effect of abutment support conditions
In order to account for the two extreme cases with respect to the shear keys, two sets of analyses were conducted on the bridges with and without shear keys. When the shear keys are modeled, they are modeled explicitly with full hysteresis definition. The results are presented for the bridge models under study (with aspect ratio of 0.3 and pinned foundations; Figures 14,15,16). It is important to note that the results are presented in terms of average of response quantities due to the application of all ground motions.
The displacement of the deck in the longitudinal (x) and transverse directions (y) under the application of 12 pairs of ground motions with the PGAs of 0.3 and 0.6 g (6 motions each) was investigated. In the longitudinal direction, the same trend was observed for the two levels of ground motions as previously demonstrated; as the skew angle increases, the displacement increases. The deck of the bridges without shear keys experienced slightly larger displacements than those with shear keys. However for straight bridges, displacements in the longitudinal direction do not seem to be affected by the absence of shear keys. It is anticipated that deformations in the longitudinal direction will not be affected significantly by the absence of shear keys, while it is expected that transverse deformations will be affected significantly.
In the transverse direction, insignificant variation of transverse displacements with the skew angle was observed at nodes 90 and 74 as shown earlier, while displacement at the node 64 (at abutment; Figure 14) increased significantly with the skew angles due to the effect of shear keys. Transverse deck displacements at the abutments for ‘without shear key’ cases were about four times than those ‘with shear keys’. Also, the average transverse deck displacements for bridges without shear keys were larger than those with shear keys for a given skew angle. At 60° skew, transverse displacements for without shear key cases were larger than without skew cases by about 60%. This clearly shows the effect of shear keys on the response and, furthermore, it shows that the demand on shear keys increase as the skew increases. It can be concluded that shear keys assist in reducing the transverse deck displacements, especially at the abutments, by a factor of more than 4. Shear keys do not affect the longitudinal deck displacement significantly.
In order to highlight the effect of the presence of shear keys on column forces, the bending moment at the top of columns (C1 and C2) about the y-y axis (M yy ) and the z-z axis (M zz ) was investigated. For M yy , a similar trend between the two cases was observed. Similar response values were obtained suggesting that shear keys are not effective in reducing the moment about y-y axis. For M zz (Figure 15), the presence or failure of shear keys is expected to affect the bridge response. The response of bridges with shear keys increases with skew, while the response of those without shear keys decreases with skew showing larger response. This observation confirms that the effectiveness of shear keys reduces as skew angles increases. It is also noted that shear keys affected the response of M zz while it did not affect M yy significantly. This is owing to the presence of shear keys which restraint deformations in the transverse direction. It is clear that shear keys can reduce the demand on columns of skewed bridges with small and moderate skew angles. The same conclusion was drawn for the two levels of ground motions. It is also noted that the axial force in columns with respect to the skew angle did not change significantly as noted earlier.
The deformation of abutment-soil springs are recorded, as deformations ‘into’ the soil (U+, passive) and ‘away’ from the soil (U−, active) with respect to the skew angle. Only the results of the four abutment springs on one side of the bridge are discussed. Herein, the effect of the presence of shear keys on U + and U − is discussed, and Figure 16 presents U − for the case of without shear keys and the two soil types considering two levels of ground motions. For U+, as the skew angle increases, the displacement decreases. The absence of shear keys is expected to increase abutment-soil interaction. Abutment springs for bridges with shear keys showed slightly larger deformation throughout. For U − (Figure 16), a different trend was observed for without shear key case, as the gap opening increases with the skew. Removing the transverse restraint (i.e., shear key) led to a larger gap opening as the skew increases. This can be attributed to the fact that deformations of abutment-soil springs, which are aligned to be perpendicular to skew, at large skew angles, is more pronounced toward the transverse direction. It was established earlier that transverse displacement increases with the skew; therefore, the demand on abutments increase. However, a more pronounced in-plane rotation at the abutments is evident from deformations at the four abutment springs for the same skew angle. Under 0.6 g level of ground motions, the ductility factors (μmax) are larger than unity, which confirms that both columns yielded but remained elastic under 0.3 g level. The shear keys have a considerable effect in reducing the ductility demand on columns of skewed bridges. In summary, removing the shear key may lead to larger gap opening and more pronounced in-plane rotation.
The absence of shear keys did not affect the displacements in the longitudinal direction significantly, while it increased those in the transverse direction dramatically by a factor of 4 at the abutments. Both columns have yielded in both cases under 0.6 g. The effectiveness of shear keys to reduce the demand on columns reduces as the skew angle becomes larger, but shear key is effective in reducing the gap opening at abutment for large skew angles. In both cases abutment-soil springs yielded while in without shear key case, gap openings were larger and increased with skew. However, if the current seismic criteria for abutment seat width, which is measured normal to the centerline of the bearing (i.e., normal to abutment back wall), were followed, no unseating would take place in these bridges. Similar observations can be made for `both soil types but with lower response quantities in case of soil type B. It is noted that abutment-soil springs or columns of skewed bridges without shear keys on soil type B may not yield even under large ground motions. These conclusions were also confirmed for bridges with larger aspect ratios (Figures 17 and 18).
Effect of aspect ratio
For this part of the study, DRAIN3DX was used to perform the nonlinear time history analyses of the twelve models with aspect ratios of 0.54 and 1.1. The analyses were conducted for only one soil type (D), the larger level of ground motions (0.6 g), and pinned bent foundations case at the presence of the shear keys.
Increasing the aspect ratio is anticipated to increase the in-plane rotation of the bridge decks with skew. This may lead to a more complex response for the skewed bridges. The demand on columns may increase due to the increase of bent forces. Also, it is crucial to monitor the response with respect to the skew angle in order to examine the effect of aspect ratio on the seismic performance. The nonlinear time history analyses were performed for the two aspect ratios, and the results are presented in the form of comparison among these two aspect ratios and the original aspect ratio (0.3).
In the longitudinal direction, for all aspect ratios, the average displacement increases as the skew angle increases. The decks of the bridges with aspect ratios of 0.54 and 1.1 experienced larger displacements than that with aspect ratio of 0.3 by about 13% and 58% respectively, at 60° skew. However, increasing the aspect ratio did not affect the trend with the skew angle as mentioned earlier, but it affected the response values.
In the transverse direction, significant increase was observed for the deck displacements at nodes 90 and 74, while as the aspect ratio increases - although small - the displacement of node 64 (at abutment; Figure 17) increased with skew angle. As the aspect ratio increases, the transverse deck displacement increases. Also, the transverse deck displacement becomes smaller from the bent location to the abutments for all aspect ratios. For all aspect ratios, there is an increase in the transverse displacement with the skew, especially, for bridges with skew larger than 30°. Nonetheless, at abutment location (node 64), deck displacement with aspect ratio of 0.54 was slightly larger than that with aspect ratio of 0.3, whereas that with aspect ratio of 1.1 was significantly larger by about 300% regardless of the skew angle. This can be attributed to the failure of the shear keys for bridges with aspect ratio of 1.1.
The bending moment of the external columns (C1 and C2) about the y-y axis (M yy ) and the z-z axis (M zz ) was investigated. For M yy , the similar trend was observed among all the cases. It was noted earlier that M yy is not affected significantly by the skew angle. Similar values of M yy with the skew was achieved by bridges with aspect ratios of 0.3 and 0.54, while larger response was achieved by bridges with the aspect ratio of 1.1. For M zz , the response increases with the skew. The response achieved by the bridges with the aspect ratio of 1.1 was consistently larger compared to the lower aspect ratios. It is also noted that the axial force in two columns with respect to the skew angle did not experience any significant variations. The envelope of average curvature ductility demand (μmax) with respect to the skew angle in both directions (μ yy and μ zz ) was investigated. For all aspect ratios, yielding took place in columns. Introducing the larger aspect ratio led to the increased ductility demand on columns especially for larger skew angles.
In terms of deformations recorded at the abutments for U+, all models followed similar trend as the response decreases when the skew angle increases except for the aspect ratio of 1.1 and when the shear keys are removed. The similar response was achieved by bridges with aspect ratios of 0.54 and 0.3, while abutment-soil springs of bridges with aspect ratio of 1.1 experienced larger response values for most of the cases. Also, yielding of abutment-soil springs was observed for all of the aspect ratios. In-plane rotations became more pronounced as the aspect ratio increases, especially, for without shear key cases. For U − (Figure 18), the gap opening tends to decrease with the skew, while the bridges with aspect ratio of 0.54 show larger gap opening than those with aspect ratio of 0.3 especially for large skew angles. Gap opening response for bridge with aspect ratio of 0.54 tends to level out with the skew for some of the cases and constantly increases with the skew for bridge with aspect ratio of 1.1. The constant increase can be attributed to the loss of shear keys. But more importantly, it is evident that the in-plane rotation of the deck becomes more pronounced for larger skew angles and larger aspect ratios. For without shear key case, the gap opening increases with the skew regardless of the aspect ratio; however, as the aspect ratio increases, the gap opening increases accompanied with more pronounced in-plane rotations.
Introducing larger aspect ratios slightly increased displacement in the longitudinal and significantly increased displacement in the transverse direction of the bridge deck. The bent forces on columns increased which led to the increased demand. However, complex response behavior was observed in bridges with larger aspect ratios. On the other hand, gap opening and closing at the abutments become more pronounced, the demand on shear keys increased, and increased in-plane deck rotations with skew were evident. Skewed bridges that were modeled without the shear keys experienced larger gap openings at the acute corner that became smaller toward the obtuse corner. The observation was valid for all skew angles and for all aspect ratios as well. Finally, the gap openings were significantly smaller in bridges modeled with the shear key elements. Uneven distribution of abutment forces may take place which can lead to progressive failure and complex global system behavior which is evident from the unequal deformations among the abutment-soil interaction springs and among the shear key springs.
Effect of foundation boundary conditions
The effect of foundation boundary conditions was studied considering the two extreme cases, as is the usual practice; namely pinned and fixed bent foundations. The nonlinear time-history analyses were performed for only soil D, with two levels of ground motions and with nonlinear shear key elements and abutment-soil springs for bridges with aspect ratio of 0.3. It was determined that the deck of the bridges with pinned bent foundation experienced larger displacements than that with fixed bent foundation by about 22% for PGA of 0.6 g regardless of skew angle. The effect of introducing fixity was larger for the larger level of ground motions, leading to larger difference between response values for any skew angle for 0.6 g case. Introducing fixity led to larger demand on column forces (moment, axial, and shear) and column ductility. Abutment-soil springs attached to bridges on pinned bent foundation showed larger displacement either into or away from abutments by largest percentage of about 36%. For fixed bent foundation and pinned bent foundation cases, yielding of shear keys was reported in an average sense under PGA of 0.6 g with lower shear key deformations for the fixed case. In summary, introducing fixed bent foundation condition reduced displacements in the longitudinal and transverse directions of the bridge deck significantly. The bent forces on columns increased, which led to the demand on columns to increase significantly. On the other hand, the deformation and force demands at the abutments and on the shear keys reduced noticeably. Also, pinned bent foundation assumption led to larger in-plane deck rotations as the skew angle increases compared to the bridges with fixed bent foundation.
Conclusions
Needless to say, one very important aspect of nonlinear analysis is the need to identify and model accurately the inelastic response characteristics of individual components. Behavior of skew highway bridges is complex, and modeling assumptions affect the predicted seismic performance. In this study, improved simplified modeling techniques were developed that are generally applicable for box girder bridges. Subsequently, various parameters were studied such as skew angle, ground motions intensity, soil type, effect of shear keys, bridge aspect ratio, and foundations boundary conditions as well as the adequacy of simplified models for dynamic analysis of skew bridges. Based on these, the following conclusions are made:
-
(1)
The use of sufficient number of fibers with fibers surrounding the column reinforcement may lead to accurate nonlinear modeling for the PMM fiber element in both of SAP2000 and DRAIN3DX. This should satisfy the condition that the cross-sectional properties of the column which are made up of fibers are close to that of the actual column. A combination of nonlinear link elements has been demonstrated to model very accurately the complex hysteretic response due to abutment-soil interaction and of the shear keys in SAP2000 resulting in reliable results as discussed in detail earlier. Improved BS models are preferable to conduct nonlinear time history analyses of skew bridges. Improved BS models are capable of capturing coupling of higher modes. A minimum of three lines of girder elements is recommended; however, the number of lines of girder elements can be increased as necessary. Also, the accuracy of BS models to capture nonlinear time history response of skew highway bridges is demonstrated. Furthermore, the time required to complete the analysis of a highly nonlinear model can be reduced by up to 70%.
-
(2)
Larger response quantities (i.e., displacements, forces) were observed with larger levels of ground motions in general. Nonetheless, bent columns as well as shear keys remained linear elastic with negligible abutment-soil interaction during the design level of excitations.
-
(3)
Relatively stiff soil conditions (soil type B) versus soft soil (soil type D) lead to smaller response for the comparable levels of excitations, regardless the skew angle.
-
(4)
It was found in general that shear keys have a predominant effect on the overall seismic response of the bridges studied herein. Shear keys are commonly used at the abutment as a fuse to provide resistance to lateral loads. Therefore, bridge columns and bents are designed to provide capacity to resist the full seismic demand assuming failure of shear keys. This study suggest that however, these assumptions may lead to an overly conservative design of the bridge columns and bents, as well as the provided design deformation capacities of the components particularly at the abutments. This study suggests that the failure of shear keys is followed by elevated transverse displacements and increased demand on columns. The ‘absence’ of shear keys may lead to increased abutment-soil structure interactions. In other words, gap opening is larger and increases with skew. It was also noted that the relative ‘effectiveness’ of shear keys in controlling the seismic response of bridges diminishes as the skew angle becomes larger. Skewed bridges that were modeled without the shear keys experienced larger gap openings at the acute corner that became smaller toward the obtuse corner. The observation was valid for all skew angles and for all aspect ratios as well. In addition, the gap openings were significantly smaller in bridges modeled with the shear key elements.
-
(5)
An overall comparison of pinned versus fixed foundation cases suggests that the former results in significantly larger deformations, whereas larger force demand on the bent component was introduced in the later case as expected.
-
(6)
Introducing larger aspect ratios slightly increased displacement in the longitudinal and significantly increased displacement in the transverse direction of the bridge deck. The bent forces on columns increased which led to the increased demand on columns. However, complex response behavior was observed in bridges with larger aspect ratios. On the other hand, gap opening and closing at the abutments become more pronounced and the demand on shear keys increased, and increased in-plane deck rotations with skew were evident.
References
AASHTO: Guide specifications for LRFD seismic bridge design. 2nd edition. American Association of State Highway and Transportation Officials, Washington, DC; 2011.
Abdel-Mohti A: Seismic response assessment and recommendations for the design of skewed highway bridges. Dissertation, University of Nevada Reno; 2009.
Abdel-Mohti A, Pekcan G: Seismic response of skewed RC box-girder bridges. Journal of Earthquake Engineering and Engineering Vibration 2008,7(4):415–426. 10.1007/s11803-008-1007-4
Bjornsson S, Stanton J, Eberhard M: Seismic response of skew bridges. In Proceedings of the 6th U.S. National Conference on Earthquake Engineering. Seattle, WA; 1997:1–12. 31 May–3 June 1997 31 May–3 June 1997
Caltrans: Seismic design criteria. Version 1.4. California Department of Transportation, Sacramento, CA; 2006. . Accessed 20 May 2007 http://www.dot.ca.gov/hq/esc/techpubs/manual/othermanual/other-engin-manual/seismic-design-criteria/sdc.html . Accessed 20 May 2007
Cheok GS, Stone WC: Behavior of 1/6-scale model bridge columns subjected to inelastic cyclic loading. J Struct Eng ACI 1990,87(6):630–638.
Computers and Structures Inc: SAP2000, Version 10.0.5. Integrated Structural Analysis and Design Software, Berkeley, CA; 2005. . Accessed 30 July 2006 http://www.csiberkeley.com/sap2000 . Accessed 30 July 2006
ElGawady M, Cofer WF, Shafiei-Tehrany R: Seismic assessment of WSDOT bridges with prestressed hollow core piles - part II. WSDOT Research Report WA-RD 732.2. Washington State Department of Transportation; 2009.
Esmaeily GA, Xiao Y: Seismic behavior of bridge columns subjected to various loading patterns. Peer Report 2002/5. College of Engineering. University of California, Berkeley; 2002.
Ghobarah AA, Tso WK: Seismic analysis of skewed highway bridges with intermediate supports. Earthquake Eng Struc 1974, 2: 235–248.
Maleki S: Deck modeling for seismic analysis of skewed slab-girder bridges. Eng Struct 2002, 24: 1315–1326. 10.1016/S0141-0296(02)00066-4
Maragakis E: A model for the rigid body motions of skew bridges. Dissertation. California Institute of Technology; 1984.
Megally SH, Silva PF, Seible F: Seismic response of sacrificial shear keys in bridge abutments. Report No. SSRP-2001/23. Department of Structural Engineering, University of California, San Diego; 2002.
Meng JY, Lui EM: Seismic analysis and assessment of a skew highway bridge. Eng Struct 2000, 22: 1433–1452. 10.1016/S0141-0296(99)00097-8
Meng JY, Lui EM: Refined stick model for dynamic analysis of skew highway bridges. J Bridge Eng 2002,7(3):184–194. 10.1061/(ASCE)1084-0702(2002)7:3(184)
Meng JY, Lui EM, Liu Y: Dynamic response of skew highway bridges. J Earthquake Eng 2001,5(3):205–223.
Muthukumar S: A contact element approach with hysteresis damping for the analysis and design of pounding in bridge. Thesis. Georgia Institute of Technology 2003.
PEER Strong Motion Database: Pacific Earthquake Engineering Research Center, Berkeley. 2000. . (25 December, 2006) http://peer.berkeley.edu/smcat . (25 December, 2006)
Prakash V, Powell GH, Campbell S: Drain-3DX: static and dynamic analysis of inelastic 3D structures. Department of Civil Engineering. University of California, Berkeley; 1994. Report No. UCB/SEMM-94/07. . Accessed date 22 August 2008 http://nisee.berkeley.edu/elibrary/Text/300016 Report No. UCB/SEMM-94/07. . Accessed date 22 August 2008
Saatcioglu M, Baingo D: Circular high-strength concrete columns under simulated seismic loading. J Struct Eng 1999,125(3):272–280. 10.1061/(ASCE)0733-9445(1999)125:3(272)
Saiidi M, Orie D: Earthquake design forces in regular highway bridges. Comput Struct 1992,44(5):1047–1054. 10.1016/0045-7949(92)90327-V
Shamsabadi A: Three-dimensional nonlinear soil-abutment-foundation-structure interaction analysis of skewed bridges. Thesis. University of Southern California 2007.
Shamsabadi A, Yan L, Martin G: Three dimensional nonlinear seismic soil foundation-structure interaction analysis of a skewed bridge considering near fault effects. USC Digital Library. 2004. . Accessed 25 August 2007 http://ebookbrowse.com/gdoc.php?id=309799094&url=b512d2b24e7a704683837b470d5e7034 . Accessed 25 August 2007
Wakefield RR, Nazmy AS, Billington DP: Analysis of seismic failure in skew RC bridge. J Struct Eng ASCE 1991,117(3):972–986. 10.1061/(ASCE)0733-9445(1991)117:3(972)
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they do not have any competing interests.
Authors’ contributions
Both authors have equal contribution. Both authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abdel-Mohti, A., Pekcan, G. Assessment of seismic performance of skew reinforced concrete box girder bridges. Int J Adv Struct Eng 5, 1 (2013). https://doi.org/10.1186/2008-6695-5-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/2008-6695-5-1