Seismic response of asymmetric systems with linear and non-linear viscous dampers

Abstract

The seismic response of linearly elastic, single-storey, one-way asymmetric building with linear and non-linear viscous dampers is investigated. The response is obtained by numerically solving the governing equations of motion. The effects of eccentricity ratio, uncoupled lateral time period, ratio of uncoupled torsional to lateral frequency and supplemental damping eccentricity ratio are investigated on peak responses which include lateral, torsional and edge displacements and their acceleration counter parts as well as control forces. To study the effectiveness of dampers, the controlled response of asymmetric system is compared with the corresponding uncontrolled response. Further, to study the effects of torsional coupling, the controlled response of asymmetric system is compared with the corresponding symmetric system. It is shown that the non-linear viscous dampers are quite effective in reducing the responses and the damper force depends on system asymmetry and supplemental damping. Also, the effectiveness of dampers significantly depends on structural and damping eccentricity ratio and torsional to lateral frequency ratio and the effects of torsional coupling are found to be more significant for torsionally flexible and strongly coupled systems. Further, effects of torsional coupling are less for asymmetric systems with non-linear dampers as compared to linear dampers.

Introduction

Post-earthquake damage assessments proved that the asymmetric buildings are much more vulnerable to the severe damage due to earthquake induced vibrations. This attracted attention of many researchers to investigate the seismic response of asymmetric buildings with supplemental energy dissipation devices to mitigate such severe damages. In past, many researchers have investigated the performance of various control techniques such as passive control viz. base isolation and supplemental dampers for lateral-torsional response control of asymmetric structures. Jangid and Datta (1994) investigated the nonlinear response of one-storey torsionally coupled base isolated system and found that if the eccentricity of the building is ignored, the effectiveness of base isolation is overestimated. Jangid and Datta (1995) investigated the stochastic response of one-storey torsionally coupled base isolated building and noticed that the effectiveness of base isolation is reduced for higher eccentricity of superstructure. Jangid (1996) studied the seismic response of one storey, one-way asymmetric base isolated structure. The effects of eccentricity ratio, torsional to lateral frequency ratio, mass ratio and coefficient of friction was studied. Jangid and Datta (1997) investigated the performance of multiple tuned mass dampers (MTMDs) for asymmetric model and found that the effectiveness of MTMDs in controlling translational response is less for an asymmetric system than corresponding symmetric system. Singh et al. (2002) derived the optimum parameters for tuned mass dampers installed in 6-story torsionally coupled building and found damper as effective in reducing the responses. De La Llera et al. (2005) proposed the weak torsional balance condition for system installed with friction dampers such as to minimize the correlation between translation and rotation. It was concluded that the maximum displacements at both edges of the building plan are always similar and less than twice the response of the nominally symmetric counterpart. Matsagar and Jangid (2010) evaluated the response of asymmetric base-isolated structure during impact with adjacent structures and without impact. It was concluded that with the increase in torsional coupling, the impact response increases, and it is mandatory to incorporate 3D analysis.

Passive viscous dampers are the efficient and well suited energy dissipation devices, which shall significantly reduce the response of buildings to earthquakes (Symans and Constantinou, 1998; Lee and Taylor, 2001). In recent past, some studies have been done to investigate the effectiveness of linear viscous dampers (LVDs) and non-linear viscous dampers (NLVDs) for symmetric and asymmetric systems. Goel (1998) studied the effects of supplemental viscous damping on seismic response of one-way asymmetric system and found that edge deformations in asymmetric systems can be reduced than those of the same edges in the corresponding symmetric systems by proper selection of supplemental damping parameters. Goel and Booker (2001) investigated the effects of supplemental viscous damping on inelastic seismic response of one-storey asymmetric building and found that the supplemental viscous damping reduces the deformation, ductility, and hysteretic energy dissipation demands in lateral load-resisting elements of asymmetric-plan systems. Lin and Chopra (2001) investigated the linear elastic, one-storey asymmetric building installed with fluid viscous dampers. It was observed that asymmetric distribution of supplemental damping is more effective in reducing the response as compared to symmetric distribution. Lin and Chopra (2002) studied the effectiveness of NLVDs for elastic single storey symmetric system. The study was carried out by assuming symmetric arrangement of dampers. It is shown that NLVDs are advantageous as they achieve the higher reduction in response with reduced damper forces. Lin and Chopra (2003) investigated the effectiveness of NLVDs and viscoelastic dampers for elastic single storey asymmetric system. They studied the effects of dampers for strongly coupled system with structural eccentricity ratio as 0.2 and for two values of exponent for damper as 0.35 and 1. The responses are also studied for different values of damping eccentricities and found that the effectiveness of supplemental damping depends on plan wise distribution of dampers. Goel (2005) studied the seismic response of one-storey, one-way asymmetric system with NLVDs. The parametric study has been done to investigate the effectiveness of NLVDs with equivalent LVDs. The responses are obtained for strongly coupled system for particular value of eccentricity ratio. Further, the response of asymmetric systems with LVDs and NLVDs are compared to evaluate the effects of non linearity and its influence on the effects of plan asymmetry. Petti and De Iuliis (2008) proposed a method to optimally locate the viscous dampers for torsional response control in asymmetric plan systems by using modal analysis techniques. It was found that optimal damping eccentricity moves from the flexible edge to the mass center by reducing the structural eccentricity.

Although, the above studies reflect the effectiveness of NLVDs in controlling the lateral-torsional responses, however, no study has been carried out to investigate effectiveness of LVDs and NLVDs in controlling the lateral, torsional and edge responses including the accelerations quantities. For the buildings, it is equally important and necessary to limit excessive torsional and edge accelerations considering the functional requirements as well as the stability of non-structural components. Hence, it shall be useful to study the effectiveness of dampers in reducing the accelerations. Also, the effectiveness of NLVDs for wide range of eccentricities is not studied so far. Moreover, in earlier findings, responses are studied for strongly coupled systems only and hence it is required to investigate the effectiveness of dampers and effects of asymmetry for torsionally flexible and torsionally stiff systems. Further, it will be interesting to study the effects of change in supplemental damping eccentricities on various displacement and acceleration responses. Moreover, an alternative approach is considered for the present study for deriving the supplemental damping coefficients in comparison to the equivalent energy approach considered by previous researchers. Furthermore, the effects of torsional coupling for various responses and damper forces for asymmetric systems in comparison to corresponding symmetric systems are also not studied in detail in past.

In this paper, the seismic response of linearly elastic, single storey, one-way asymmetric building is investigated under different real earthquake ground motions. The specific objectives of the study are summarized as (i) to study the comparative performance of LVDs and NLVDs in controlling lateral, torsional and edge displacements as well as their acceleration counterparts, (ii) to study the effects of torsional coupling on the effectiveness of LVDs and NLVDs, and (iii) to investigate the influence of important parameters on the effectiveness of LVDs and NLVDs for asymmetric systems. The important parameters considered are eccentricity ratio of superstructure, uncoupled lateral time period, ratio of uncoupled torsional to lateral frequency and supplemental damping eccentricity ratio.

Structural model and solution of equations of motion

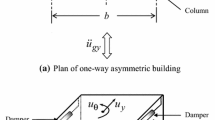
The system considered is an idealized one-storey building which consists of a rigid deck supported on columns as shown in Figure 1. Following assumptions are made for the structural system under consideration: (i) floor of the superstructure is assumed as rigid, (ii) force-deformation behaviour of superstructure is considered as linear and within elastic range and (iii) the structure is excited by uni-directional horizontal component of earthquake ground motion. The mass of deck is assumed to be uniformly distributed and hence centre of mass (CM) coincides with the geometrical centre of the deck. The columns are arranged in a way such that it produces the stiffness asymmetry with respect to the CM in one direction and hence, the centre of rigidity (CR) is located at an eccentric distance, $e_x$ from CM in x-direction. The system is symmetric in x-direction and therefore, two degrees-of-freedom are considered for model namely the lateral displacement in y-direction, u _y and torsional displacement, $u_{\theta }$ as represented in Figure 1. The governing equations of motion of the building model with coupled lateral and torsional degrees-of-freedom are obtained by assuming that the control forces provided by the dampers are adequate to keep the response of the structure in the linear range. The equations of motion of the system in the matrix form are expressed as

$$Mü+C\dot{u}+Ku=-M\Gamma {ü}_g+\Lambda F$$

(1)

where $M$, $C$and $K$ are mass, damping and stiffness matrices of the system, respectively; $u={\left\{u_y{u}_{\theta }\right\}}^{\text{T}}$is the displacement vector; $\Gamma$ is the influence coefficient vector; ${ü}_g={\left\{{ü}_{\mathit{gy}}0\right\}}^T$ is ground acceleration vector; ${ü}_{\mathit{gy}}$ is ground acceleration in y-direction; $\Lambda$ is the matrix that defines the location of control devices; $F={\left\{F_{\mathit{dy}}{F}_{\mathit{d\theta }}\right\}}^T$ is the vector of control forces; and F _dy and $F_{\mathit{d\theta }}$ are resultant control forces of dampers along y- and $\theta$- direction, respectively.

Figure 1

Plan and isometric view of one-way asymmetric system showing arrangement of dampers. (a) Plan of one-way asymmetric system. (b) Isometric view of system showing arrangement of dampers.

The mass matrix can be expressed as,

$$M=\left[\begin{array}{cc}\hfill m\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill m{r}^2\hfill \end{array}\right]$$

(2)

where m represents the lumped mass of the deck; and $r$ is the mass radius of gyration about the vertical axis through CM which is given by, $r=\sqrt{\left(a^2+b^2\right)/12}$; where a and $b$ are the plan dimensions of the building.

The stiffness matrix of the system is modified as follows (Goel, 1998)

$$K=K_y\left[\begin{array}{cc}\hfill 1\hfill & \hfill e_x\hfill \\ \hfill e_x\hfill & \hfill {e_x}^2+r^2{{\Omega }_{\theta }}^2\hfill \end{array}\right]$$

(3)

$$e_x=\frac{1}{K_y}{\displaystyle \sum _i{K}_{\mathit{yi}}{x}_i}\text{and}{\Omega }_{\theta }=\frac{{\omega }_{\theta }}{{\omega }_y}$$

(4)

$${\omega }_{\theta }=\sqrt{\frac{K_{\mathit{\theta r}}}{m{r}^2}}\text{and}{\omega }_y=\sqrt{\frac{K_y}{m}}$$

(5)

$$\begin{array}{c}{K}_{\mathit{\theta r}}=K_{\mathit{\theta \theta }}-{e_x}^2{K}_y\text{and}{K}_{\mathit{\theta \theta }}\\ ={\displaystyle \sum _i{K}_{\mathit{xi}}{y_i}^2}+{\displaystyle \sum _i{K}_{\mathit{yi}}{x_i}^2}\end{array}$$

(6)

where $K_y$ denotes the total lateral stiffness of the system in y-direction; e _x is the structural eccentricity between CM and CR of the system; Ω _θ is the ratio of uncoupled torsional to lateral frequency of the system; $K_{\mathit{yi}}$ indicates the lateral stiffness of i^th column in y-direction; $x_i$ is the x-coordinate distance of i^th element with respect to CM; ω _y is uncoupled lateral frequency of the system; ${\omega }_{\theta }$ is uncoupled torsional frequency of the system; $K_{\mathit{\theta r}}$ is torsional stiffness of the system about a vertical axis at the CR; $K_{\mathit{\theta \theta }}$ is torsional stiffness of the system about a vertical axis at the CM; $K_{\mathit{xi}}$ indicates the lateral stiffness of i^th column in x-direction; and y _i is the y-coordinate distance of i^th element with respect to CM.

Let $e_d$ represent the supplemental damping eccentricity defined as the distance between CM and centre of supplemental damping (CD) which reflects the lack of symmetry in the damper properties about the y-axis and expressed as

$$e_d=\frac{1}{C_d}{\displaystyle \sum _i{C}_{\mathit{di}}{x}_i}$$

(7)

where $C_d$ is the total damping coefficient of damper system along y-axis; and $C_{\mathit{di}}$ is the damping coefficient of the i^th damper along y-axis. The value of $C_d$ is calculated as $C_d=2m{\omega }_y{\xi }_d$, where, ${\xi }_d$ is the supplemental damping ratio.

The damping matrix of the system is not known explicitly and it is constructed from the Rayleigh’s damping considering mass and stiffness proportional as,

$$C=a_{0}M+a_{1}K$$

(8)

in which a₀ and $a_1$ are the coefficients depends on damping ratio of two vibration modes. For the present study 5% damping is considered for both modes of vibration of system.

The governing equations of motion are solved using the state space method (Hart and Wong, 2000; Lu, 2004) and re-written as

$$\dot{z}=Az+BF+E{ü}_g$$

(9)

where $z={\left\{u\dot{u}\right\}}^{\text{T}}$is a state vector; A is the system matrix; $B$ is the distribution matrix of control forces; and $E$ is distribution matrix of excitations. These matrices are expressed as,

$$\begin{array}{c}A=\left[\begin{array}{cc}\hfill 0\hfill & \hfill I\hfill \\ \hfill -M^{-1}K\hfill & \hfill -M^{-1}C\hfill \end{array}\right];\\ B=\left[\begin{array}{l}0\\ M^{-1}\Lambda \end{array}\right]\text{and}E=-\left[\begin{array}{l}0\\ \Gamma \end{array}\right]\end{array}$$

(10)

in which $I$ is the identity matrix.

The Eq. (9) is discretized in time domain and the excitation and control forces are assumed to be constant within any time interval, the solution may be written in an incremental form (Hart and Wong, 2000; Lu, 2004),

$$z\left[k+1\right]=A_{d}z\left[k\right]+B_{d}F\left[k\right]+E_d{ü}_g\left[k\right]$$

(11)

where $k$denotes the time step; and $A_d=e^{\mathit{A\Delta t}}$ represents the discrete-time system matrix with $\mathit{\Delta t}$ as time interval. The constant coefficient matrices $B_d$and $E_d$are discrete-time counterparts of matrices $B$and E and can be written as

$$B_d=A^{-1}\left(A_d-I\right)B\text{and}{E}_d=A^{-1}\left(A_d-I\right)E$$

(12)

Modeling of fluid viscous damper

Fluid dampers operate on the principle of fluid flow through orifices and provide forces that always resist structure motion during a seismic event. Figure 2 shows a schematic and mathematical model of typical fluid viscous damper. A typical viscous damper consists of a cylindrical body and central piston which strokes through a fluid filled chamber. The commonly used fluid is silicone based fluid which ensures proper performance and stability. The differential pressure generated across the piston head results in the damper force (Symans and Constantinou, 1998; Lee and Taylor, 2001).

Figure 2

Schematic and mathematical model of the fluid viscous damper. (a) Schematic diagram of fluid viscous damper (Symans and Constantinou 1998). (b) Mathematical model of fluid viscous damper.

The force in a viscous damper, $F_{\mathit{di}}$ (=$F_{\mathit{df}}$ or F _ds ) is proportional to the relative velocity between the ends of a damper and given by

$$F_{\mathit{di}}=C_{\mathit{di}}{\left|{\dot{u}}_{\mathit{di}}\right|}^{\alpha }sgn\left({\dot{u}}_{\mathit{di}}\right)$$

(13)

where, $C_{\mathit{di}}$ is damper coefficient of the i^th damper, ${\dot{u}}_{\mathit{di}}$ is relative velocity between the two ends of a damper which is to be considered corresponding to the position of dampers, α is the damper exponent ranging from 0.2 to 1 for seismic applications (Soong and Dargush, 1997) and $sgn\left(·\right)$ is signum function. The value of exponent is primarily controlled by the design of piston head orifices. When $\alpha$ = 1, a damper is called as linear viscous damper (LVD) and with the value of $\alpha$ smaller than unity, a damper will behave as non-linear viscous damper (NLVD). Dampers with α larger than unity have not been seen often in seismic practical applications.

Numerical study

The seismic response of linearly elastic, idealized single-storey, one-way asymmetric building installed with passive fluid viscous dampers is investigated by numerical simulation study. The response quantities of interest are lateral and torsional displacements of floor mass obtained at the CM ($u_y$ and $u_{\theta }$), displacements at stiff and flexible edges of building (u _ys and $u_{\mathit{yf}}$), lateral and torsional accelerations of floor mass obtained at the CM (${ü}_y$ and ${ü}_{\theta }$), accelerations at stiff and flexible edges of building (${ü}_{\mathit{ys}}$ and ü _yf ), control forces of the dampers installed at stiff edge ($F_{\mathit{ds}}$) and at flexible edge ($F_{\mathit{df}}$) of building as well as resultant damper force,$F_{\mathit{dy}}$($=F_{\mathit{ds}}+F_{\mathit{df}}$). The response of the system is investigated under following parametric variations: structural eccentricity ratio ($e_x/r$), uncoupled lateral time period of system (T _y  = 2π/ω _y ), ratio of uncoupled torsional to lateral frequency of the system (${\Omega }_{\theta }={\omega }_{\theta }/{\omega }_y$) and supplemental damping eccentricity ratio ($e_d/r$). The peak responses are obtained corresponding to the important parameters which are listed above for four considered earthquake ground motions namely, Imperial Valley (1940), Loma Prieta (1989), Northridge (1994) and Kobe (1995) with corresponding peak ground acceleration (PGA) values of 0.31 g, 0.96 g, 0.89 g and 0.82 g as per the details summarized in Table 1. The average values of peak responses from four earthquakes are obtained and parametric study is carried out based on these average trends such as to have more definite study under the range of seismic ground motions. For the study carried out herein, the aspect ratio of plan dimension is kept as unity and the mass and stiffness of system are considered such as to have required lateral time period. Further, total two fluid viscous dampers (one at each edge) are installed in the building as shown in Figure 1.

Table 1 Details of earthquake motions considered for the numerical study

In order to study the effectiveness of control system and effects of torsional coupling, the responses are expressed in terms of indices, R _e and $R_t$ defined as follows:

$$R_e=\frac{\text{Peak response of controlled asymmetric system}}{\text{Peak response of corresponding uncontrolled system}}$$

(14)

$$R_t=\frac{\text{Peak response of controlled asymmetric system}}{\text{Peak response of corresponding symmetric system}}$$

(15)

The value of R _e less than unity indicates that the control system is effective in reducing the responses. On the other hand, the value of $R_t$ reflects the effects of torsional coupling on the effectiveness of control system for asymmetric system as compared to corresponding symmetric system. The value of R _t greater than unity indicates that the response of asymmetric system increases due to torsional coupling and hence the effectiveness of control system is less for asymmetric system as compared to corresponding symmetric system.

In order to investigate the effectiveness of LVDs and NLVDs, the velocity exponent, $\alpha$ as expressed in Eq. (13) is varied from 0.2 (highly non-linear) to 1 (linear) for the systems with ${\Omega }_{\theta }$ = 0.5 (torsionally flexible), ${\Omega }_{\theta }$ = 1 (strongly coupled) and ${\Omega }_{\theta }$ = 2 (torsionally stiff). The responses are obtained for system with $T_y$= 1 s and intermediate value of eccentricity ratio, $e_x/r$ = 0.3 under four considered earthquakes and variations are shown for the average responses in Figure 3. The supplemental damping ratio, ξ _d is considered as 20%. In the present study, the effects of supplemental damping eccentricity ratio, $e_d/r$ is investigated separately in later sections, hence unless it is specified for the other parametric study, the value of e _d /r is taken as zero implying the symmetric arrangement of dampers on both sides. The response ratios, $R_e$ are obtained for torsional displacement ($u_{\theta }$), stiff edge displacement (u _ys ), flexible edge displacement ($u_{\mathit{yf}}$) as well as their accelerations counterparts (i.e. ${ü}_{\theta }$ , ${ü}_{\mathit{ys}}$ and ${ü}_{\mathit{yf}}$) and its variations against α are plotted. It can be observed from the figure that with the increase in values of $\alpha$, the ratio, $R_e$ increases for responses u _θ , $u_{\mathit{ys}}$ and $u_{\mathit{yf}}$ corresponding to all values of ${\Omega }_{\theta }$. On the other hand, for torsional and edge acceleration responses, the variations of $R_e$ remains less sensitive to α. Thus, the effectiveness of fluid viscous dampers decreases in reducing various displacement responses with increase in $\alpha$. Further, figure also shows the variation of peak control forces of dampers located at stiff edge ($F_{\mathit{ds}}$), at flexible edge (F _df ) as well as resultant damper force ($F_{\mathit{dy}}$). The damper forces are normalized with the weight of deck, $W$. It is observed that with the increase in values of $\alpha$, $F_{\mathit{ds}}$ and $F_{\mathit{df}}$ increases except for torsionally flexible system, in which $F_{\mathit{df}}$ decreases. Moreover, $F_{\mathit{dy}}$ slightly decreases initially and then increases with further increase in $\alpha$ and this trend is more significant for torsionally stiff systems. Also, the optimum range for the value of α is found to be 0.3 to 0.6 considering the damper forces. Further, the damper force in NLVDs ($\alpha$ < 1) is smaller than corresponding force in LVDs ($\alpha$ = 1) with higher reduction in responses achieved with NLVDs for system with $T_y$= 1 s. Thus, the difference between the resultant damper force of NLVDs and LVDs is more for torsionally stiff system as compared to torsionally flexible and strongly coupled systems.

Figure 3

Effect of exponent, α on response ratio, R _e for various displacement and acceleration responses and damper forces.

In order to study the effects of supplemental damping ratio, ${\xi }_d$ for LVDs and NLVDs, the variations of R _e against ${\xi }_d$ (which is varied from 0 to 80%) are shown in Figures 4 and 5. The value of $R_e$ = 1 corresponding to ξ _d = 0 is representing the uncontrolled response. The responses are obtained for the system with $T_y$= 1 s and $e_x/r$ = 0.3 for three values of ${\Omega }_{\theta }$ = 0.5, 1 and 2 are shown in Figures 4(a), (b) and 5(a), respectively. The responses are plotted for four values of $\alpha$ (i.e. 0.35, 0.5, 0.7 and 1 representing the NLVD to LVD) which have been seen for the seismic practical applications. It can be observed from the first set of rows of Figures 4(a), (b) and 5(a) that with the increase in ${\xi }_d$, the ratio, $R_e$ decreases for torsional ($u_{\theta }$) and edge displacement (u _ys and $u_{\mathit{yf}}$) responses corresponding to all values of $\alpha$. This implies that the effectiveness of control system increases with the increase in ξ _d . Moreover, as observed in earlier section, values of $R_e$ corresponding to $\alpha$ = 1 (LVD) are highest followed by the corresponding values obtained from $\alpha$ = 0.7, 0.5 and 0.35 (NLVDs). Furthermore, the second set of rows of Figures 4(a), (b) and 5(a) represents the variations of $R_e$ for torsional (${ü}_{\theta }$) and edge accelerations (${ü}_{\mathit{ys}}$ and ü _yf ). It is observed that for the systems with ${\Omega }_{\theta }$ = 0.5 and 1, ratio, $R_e$ for ü _yf first decreases and then increases with further increase in ${\xi }_d$. This means, there exist an optimum value of ξ _d for the flexible edge accelerations, which is one of the important response quantities. On the other hand, for ${ü}_{\theta }$ and ${ü}_{\mathit{ys}}$, ratio, $R_e$ decreases with increase in ${\xi }_d$. However, the variations for R _e remains very less sensitive beyond the supplemental damping ratio equal to 30% especially for reducing the edge accelerations. Further, it is noticed that the NLVDs are little more effective than LVDs in reducing the stiff edge accelerations and torsional accelerations for systems with ${\Omega }_{\theta }$ = 0.5 and 1, whereas, for torsionally stiff system, the effectiveness of NLVDs is less as compared to LVDs in reducing torsional accelerations. Further, in general, it is also observed that the reduction in various responses is higher in the range of ${\xi }_d$ when it is varied from 0 to 30% as compared to the reduction observed beyond 30%. In addition, Figure 5(b) shows the variations of normalized damper force ($F_{\mathit{dy}}$) against ${\xi }_d$. It is observed that with increase in ξ _d , the damper force increases for all values of $\alpha$, which is as expected. Thus, the increase in supplemental damping ratio increases the effectiveness of dampers in reducing torsional displacement and accelerations, stiff edge displacement and accelerations as well as flexible edge displacements for systems with ${\Omega }_{\theta }$ = 0.5, 1 and 2. On the other hand, the effectiveness decreases for higher supplemental damping ratio in reducing flexible edge accelerations for systems with Ω _θ = 0.5 and 1. Further, resultant damper force of NLVDs is less than the corresponding force of LVDs in the initial range of supplemental damping ratio (up to 30%) and for higher values of damping ratio, the reverse trend is observed.

Figure 4

Effect of ξ _d on R _e for various displacement and acceleration responses. (a) for Ω_θ = 0.5. (b) For Ω_θ =1.

Figure 5

Effect of ξ _d on R _e and normalized resultant damper force. (a) For Ω_θ = 2. (b) For normalized resultant damper force (F _dy ).

Figure 6 shows the time histories of various displacement and acceleration responses of uncontrolled system compared with corresponding system controlled with LVDs ($\alpha$ = 1) and NLVDs ($\alpha$ = 0.35). The responses are shown for the system with T _y = 1 s, ${\Omega }_{\theta }$ = 1 and $e_x/r$= 0.3 under Kobe, 1995 earthquake. The significant reduction in displacement and acceleration responses at CM, at flexible and stiff edges as well as torsional responses is observed with dampers and the NLVDs are found to be little more effective than LVDs.

Figure 6

Time histories for various uncontrolled and controlled displacements and accelerations under Kobe, 1995 earthquake.

Figure 7 represents the hysteresis loops for the normalized damper force with displacement and velocity for LVDs and NLVDs placed at stiff and flexible edges of the system with T _y = 1 s, ${\Omega }_{\theta }$ = 1 and $e_x/r$ = 0.3 under Kobe, 1995 earthquake. It can be observed from the force-velocity loops that the dampers with $\alpha$ = 1 exhibits a linear behavior whereas, the dampers with $\alpha$ = 0.35 exhibits a non-linear behavior.

Figure 7

Typical hysteresis loops for LVDs and NLVDs under Kobe, 1995 earthquake.

In earlier discussions, the effectiveness of control system is studied for the building with intermediate eccentricity. Hence, further it is important and necessary to investigate the effectiveness of dampers in reducing various responses for systems with lower to higher eccentricity range. In order to investigate this, variations of ratio, R _e against eccentricity ratio, $e_x/r$ are shown in Figure 8 for system with $T_y$ = 1 s and Ω _θ = 0.5, 1 and 2. It is clear from the earlier finding that the lesser value of exponent, $\alpha$ gives the higher reduction in responses whereas, higher value of $\alpha$ leads to an increase in damper force. Also, the significant reduction in responses are obtained when ${\xi }_d$ is near to 20%, whereas, the higher values of that increases the damper force as well as flexible edge accelerations. Hence, for the study carried out from here onwards, ${\xi }_d$ and $\alpha$ are considered as 20% and 0.35, respectively. It can be observed from the Figure 8 that with increase in e _x /r, the ratio, $R_e$ increases for torsional responses, $u_{\theta }$ and ü _θ . This implies that the effectiveness of dampers reduces for the system with higher eccentricities in reducing torsional responses. Moreover, it can be seen that the NLVDs perform better than LVDs for the range of $e_x/r$ values in reducing various displacements and accelerations except for ${ü}_{\theta }$ for the system with Ω _θ = 2 and ${ü}_{\mathit{yf}}$ for system with ${\Omega }_{\theta }$ = 0.5 in which LVDs perform better than NLVDs. Further, in general, it is observed that the values of R _e for various displacement responses are lesser than the corresponding acceleration responses. This show the dampers are more effective in reducing the displacement responses as compared to acceleration responses. Furthermore, the variation in $R_e$ is more sensitive to the change in $e_x/r$ for acceleration responses as compared to displacement responses for NLVDs. Thus, the effectiveness of NLVDs is more sensitive to the eccentricity ratio for acceleration responses as compared to displacement responses. This phenomenon is more predominant for torsionally flexible and strongly coupled systems.

Figure 8

Effect of eccentricity on response ratio, R _e for various displacement and acceleration responses.

In order to study the effectiveness of dampers for building ($e_x/r$ = 0.3) with different lateral time periods, the variations of $R_e$ against T _y are shown in Figure 9. It is observed that the values of $R_e$ comes out to be less than unity for all responses for considered range of $T_y$, in general, which shows the effectiveness of dampers. It is further noticed that R _e for displacement and acceleration responses increases with increase in $T_y$, in general. However, variations in values of $R_e$ are more sensitive and significant for acceleration responses as compared to displacement responses for NLVDs. It is also observed that NLVDs are more effective in reducing torsional responses ($u_{\theta }$ and ${ü}_{\theta }$) for strongly coupled system (Ω _θ = 1) followed by systems with ${\Omega }_{\theta }$= 0.5 and 2. Moreover, for systems with Ω _θ = 1, higher reduction in ${ü}_{\theta }$ can be achieved with NLVDs as compared to LVDs and for ${\Omega }_{\theta }$ = 2, higher reduction in ü _θ can be achieved with LVDs. For laterally stiff systems with ${\Omega }_{\theta }$ = 0.5, the NLVDs perform better than LVDs in reducing ${ü}_{\theta }$ and ü _yf , whereas for laterally flexible systems with ${\Omega }_{\theta }$ = 0.5, LVDs perform better than NLVDs. Thus, effectiveness of dampers decreases with increase in lateral flexibility of building and effectiveness of NLVDs is more in reducing displacement responses as compared to accelerations. Further, NLVDs are more effective than LVDs for laterally flexible to stiff systems with ${\Omega }_{\theta }$= 0.5, 1 and 2 in reducing various displacements. On the other hand, the comparative performance of LVDs and NLVDs may vary depending on the value of ${\Omega }_{\theta }$ and $T_y$ for reducing acceleration responses.

Figure 9

Effect of lateral time period, T _y on response ratio, R _e for various displacement and acceleration responses.

Figure 10 (a) shows the variation of normalized damper forces against e _x /r for system with $T_y$ = 1 s. It is observed that for the system with ${\Omega }_{\theta }$= 0.5, the stiff edge damper force, F _ds increases initially and then decreases with further increase in $e_x/r$, whereas an opposite trend is observed for flexible edge damper force, $F_{\mathit{df}}$. Further, for systems with Ω _θ = 1 and 2, $F_{\mathit{ds}}$ decreases and $F_{\mathit{df}}$ increases with increase in $e_x/r$ for both values of $\alpha$. It is further observed that for systems with Ω _θ = 0.5, 1 and 2, resultant damper force, $F_{\mathit{dy}}$ decreases with increase in eccentricity ratio. Further, for systems with ${\Omega }_{\theta }$= 0.5 and 1, up to an intermediate eccentricity, F _dy for NLVDs is less than corresponding force for LVDs, whereas for systems with higher eccentricities, the force in NLVDs increases as compared to LVDs. Moreover, for system with ${\Omega }_{\theta }$= 2,$F_{\mathit{dy}}$ is less for NLVDs as compared to LVDs corresponding to all values of e _x /r. In addition, Figure 10 (b) shows the variations of damper forces against lateral time period, $T_y$. It can be observed that for laterally stiff systems ($T_y$ < 0.75 s), $F_{\mathit{dy}}$ for NLVDs is more than corresponding force of LVDs, whereas for laterally flexible systems ($T_y$ > 0.75 s), F _dy for NLVDs is lesser than the corresponding force of LVDs. The similar trends are also observed for individual damper forces i.e. $F_{\mathit{ds}}$ and $F_{\mathit{df}}$. Thus, the difference between damper force in NLVDs and corresponding force in LVDs strongly depends on structural eccentricity for torsionally flexible and strongly coupled systems as compared to torsionally stiff systems. Also, for laterally stiff systems ($T_y$ < 0.75 s), damper force for NLVDs is more than corresponding force of LVDs. On the other hand, for laterally flexible systems ($T_y$ > 0.75 s), reverse trend is observed and as the lateral flexibility of building increases, the difference between damper force of NLVDs and LVDs decreases.

Figure 10

Variation of normalized damper forces for NLVDs and LVDs. (a) Variation against e _x /r. (b) Variation against T _y .

In the study carried out up to this section, the damping coefficients of both the dampers are kept constant which is implying the zero damping eccentricity. Now, in this section, to investigate the effects of supplemental damping eccentricity, the damping coefficients of both edge dampers are varied such as to have required damping eccentricity, $e_d$ as expressed by Eq. (7). Thus, the variations of $R_e$ against supplemental damping eccentricity ratio, $e_d/r$ for lateral, edge and torsional displacements and accelerations are shown in Figures 11 and 12, respectively. The figures are plotted for four values of $T_y$ (= 0.5, 1, 2 and 3 s). The other parameters considered are e _x /r = 0.3, ${\xi }_d$ = 20% and α = 0.35. The ratio, $e_d/r$ is varied from negative extreme (i.e. all dampers are located at flexible edge of building) to positive extreme (i.e. all dampers are located at stiff edge of building). It is observed from the first set of rows of Figures 11 and 12, that the ratio, $R_e$ for u _θ and ${ü}_{\theta }$, initially decreases with the increase in $e_d/r$, attains some minimum value near to $e_d/r$ = 0 and then increases with further increase in $e_d/r$. For the systems with Ω _θ = 2, the extreme values of $e_d/r$ leads to very high torsional responses, sometimes higher than the uncontrolled responses. Further, it is observed from second set of rows of Figures 11 and 12 that for laterally stiff systems with ${\Omega }_{\theta }$ = 0.5, 1 and 2, values of $e_d/r$ in the range of 0 to - 0.3 (i.e. opposite to $e_x/r$ =0.3) leads to the higher reduction in lateral displacement at CM, u _y and for laterally flexible systems, $e_d/r$ in the range of 0 to 0.3 leads to the higher reduction in $u_y$. Also, the variation in $R_e$ for $u_y$ is more sensitive to the change in e _d /r for systems with ${\Omega }_{\theta }$ = 0.5 and 1. Moreover, positive values of $e_d/r$ (i.e. CD is on same side of CR) lead to the higher reduction in lateral acceleration at CM, ü _y .

Figure 11

Effect of supplemental damping eccentricity e _d / r on ratio R _e for various displacement responses.

Figure 12

Effect of supplemental damping eccentricity e _d / r on ratio R _e for various accelerations responses.

Further, from third set of rows of Figures 11 and 12 it is observed that as the $e_d/r$ varies from negative to positive, the ratio, $R_e$ for u _ys continuously decreases for all values of $T_y$ as well as ${\Omega }_{\theta }$. This implies that the control system is more effective in reducing u _ys , when CD is on same side of CR and CD should be as far as away from the CM to achieve higher reduction in $u_{\mathit{ys}}$. The similar trends are also observed for stiff edge acceleration, ü _ys for the laterally stiff system ($T_y$ = 0.5). On the other hand, for laterally flexible systems, ratio, $R_e$ for ü _ys initially decreases, attains some minimum value (near to the value of $e_d/r$ equal to zero or positive) and then increases with further increase in $e_d/r$. As the lateral flexibility of building increases, the value of $e_d/r$ for which $R_e$ for ${ü}_{\mathit{ys}}$ attains the minimum values slightly shift from positive end to zero. Similarly, from the last set of row of Figures 11 and 12 it is observed that as the $e_d/r$ varies from negative to positive, the ratio, R _e for $u_{\mathit{yf}}$ continuously increases for all values of $T_y$. This implies that the control system is more effective in reducing flexible edge displacement, when CD is on opposite side of CR and CD should be as far as away from the CM to achieve higher reduction in $u_{\mathit{yf}}$. The similar trends are also observed for flexible edge acceleration, ü _yf for the laterally stiff system ($T_y$ = 0.5). For laterally flexible system with ${\Omega }_{\theta }$ = 0.5, higher reduction in ${ü}_{\mathit{yf}}$ can be achieved with positive values of $e_d/r$ (i.e. CD is on the same side of CR), whereas for systems with Ω _θ = 1 and 2, higher reduction in ${ü}_{\mathit{yf}}$ can be achieved when $e_d/r$ remains near to the value of zero. Moreover, it is observed that for torsionally stiff (Ω _θ = 2) and laterally flexible systems ($T_y$ = 3), by positioning the CD at the edges or near to either of the edges leads to the significant increase in torsional displacement and torsional as well as edge accelerations as compared to uncontrolled responses. Hence for such systems, it is always preferable to keep the CD near to the CM. Further, in general, corresponding to all values of $e_d/r$, the reduction in various responses are higher for the system with T _y = 0.5, followed by $T_y$ = 1, 2 and 3. Thus, the symmetric arrangement of dampers leads to higher reduction in torsional responses for building with intermediate eccentricity. For laterally stiff systems, location of CD on the same side of CR leads to higher reduction in stiff edge displacement and acceleration and CD is on the opposite side of CR leads to the higher reduction in flexible edge displacement and acceleration. In order to achieve this, CD should be as far as way from CM. For laterally flexible systems, CD on same side of CR and near to CM, leads to higher reduction in edge accelerations, whereas, locating CD at the extreme distance from CM on the side of CR leads to higher reduction in stiff edge displacement and opposite for flexible edge displacement.

In addition to the parametric study carried out to investigate the effectiveness of control system, it is equally important to study the effects of torsional couplings on the effectiveness of control system for asymmetric buildings as compared to corresponding symmetric buildings. Hence, the variations of response ratio, R _t (the ratio between peak response of controlled asymmetric and corresponding symmetric system) for various displacements and accelerations are plotted against eccentricity ratio, $e_x/r$ in Figure 13 for the system with $T_y$ = 1. It is observed that for systems with ${\Omega }_{\theta }$ = 0.5, 1 and 2, ratio, $R_t$ for $u_y$ and ${ü}_y$ decreases with increase in e _x /r and remains less than unity. This implies that $u_y$ and ${ü}_y$ reduces due to torsional coupling and hence effectiveness of control system is more for asymmetric system as compared to corresponding symmetric system. Thus, by neglecting the eccentricity, the effectiveness of control system will be underestimated for $u_y$ and ${ü}_y$ for asymmetric systems as compared to corresponding symmetric systems. Moreover, for torsionally flexible systems up to an intermediate eccentricity (i.e. e _x /r < 0.4), $R_t$ for $u_{\mathit{ys}}$ first increases and then decreases with further increase in eccentricity ratio. For flexible edge displacement, $u_{\mathit{yf}}$, ratio, $R_t$ remains less than unity up to an intermediate eccentricity and then increases for higher eccentricity. This implies that for torsionally flexible systems with an intermediate eccentricity, $u_{\mathit{ys}}$ increases and $u_{\mathit{yf}}$ reduces due to torsional coupling and hence effectiveness of control system is less for asymmetric system and by ignoring the eccentricity, effectiveness will be overestimated for $u_{\mathit{ys}}$and underestimated for u _yf . On the other hand,, for the system with higher eccentricity, $u_{\mathit{ys}}$ decreases and $u_{\mathit{yf}}$ increases and u _yf increases. This implies that, the effectiveness of control system is more for asymmetric system in reducing $u_{\mathit{ys}}$ and it will be underestimated by ignoring the effects of torsional couplings and the effectiveness is less for reducing u _yf as compared to the corresponding symmetric systems and it will be overestimated. It is further observed that for systems with ${\Omega }_{\theta }$ = 1 and 2, with the increase in eccentricity, $R_t$ for $u_{\mathit{ys}}$ decreases and for $u_{\mathit{yf}}$ it increases. Hence, by neglecting the effects of eccentricity, the effectiveness of control system will be underestimated for reducing $u_{\mathit{ys}}$ and overestimated for $u_{\mathit{yf}}$ as compared to the corresponding symmetric systems. Furthermore, it is observed that for the system with Ω _θ = 0.5 and 1, with increase in e _x /r, the ratio, $R_t$ for stiff edge acceleration, ü _ys increases and remains more than unity whereas for flexible edge acceleration, ${ü}_{\mathit{yf}}$, it decreases and remains less than unity. This implies that for asymmetric systems, ${ü}_{\mathit{ys}}$ increases and ${ü}_{\mathit{yf}}$ reduces due to torsional coupling. Hence, the effectiveness of control system is less for asymmetric system in reducing ${ü}_{\mathit{ys}}$ and it will be underestimated by ignoring the asymmetry and the effectiveness is more for reducing ü _yf and will be underestimated. Further, for system with ${\Omega }_{\theta }$= 2, the ratio, $R_t$ for ü _ys and ${ü}_{\mathit{yf}}$ remains near to the unity. Thus, the effects of torsional coupling are more pronounced for torsionally flexible and strongly coupled systems as compared to torsionally stiff systems while estimating the effectiveness of control system for asymmetric systems in reducing edge displacements and edge accelerations as compared to the corresponding symmetric systems.

Figure 13

Effect of eccentricity on response ratio, R _t for various displacement and acceleration responses and damper forces.

Moreover, in addition to structural responses, the damper forces also play an important role while studying the effects of torsional coupling. In order to investigate these, variations of ratio, R _t are shown in Figure 13 for peak control forces. It is observed that for torsionally flexible systems, the ratio, $R_t$ for F _ds remains more than unity except for system with very high eccentricities and for $F_{\mathit{df}}$, it remains less than unity whereas, for strongly coupled and torsionally stiff systems, the ratio, $R_t$ for $F_{\mathit{ds}}$ remains less than unity and for $F_{\mathit{df}}$, it remains more than unity. Thus, by neglecting the eccentricity for torsionally flexible systems, the control forces at flexible edge, will be overestimated and at stiff edge, that will be underestimated as compared to corresponding symmetric systems. Similarly, for strongly coupled and torsionally stiff systems, $F_{\mathit{df}}$ will be underestimated and $F_{\mathit{ds}}$ will be overestimated by ignoring the eccentricity. Moreover, it can be noticed that with increase in e _x /r, ratio, $R_t$ for $F_{\mathit{dy}}$ decreases and remains less than unity for the systems with Ω _θ = 0.5, 1 and 2. This implies that the total damper forces of asymmetric system remains always less than those of corresponding symmetric system.

In this section, to study the effects of torsional coupling for laterally stiff to laterally flexible systems, the ratio, $R_t$ for various responses are plotted against $T_y$ (varied from 0.1 to 3 s) in Figure 14. The discussion presented herein mainly focuses on observations based on NLVDs. It is observed that for laterally stiff systems ($T_y$< 0.75 s) with ${\Omega }_{\theta }$= 0.5, 1 and 2, ratio, $R_t$ for u _ys is less than unity and for $u_{\mathit{yf}}$, it remains more than unity and hence $u_{\mathit{ys}}$ of laterally stiff asymmetric systems is lower $u_{\mathit{yf}}$ is more than those of corresponding symmetric systems. It is further noticed that for laterally flexible systems with ${\Omega }_{\theta }$= 0.5, $R_t$ for $u_{\mathit{yf}}$ remains less than unity and for $u_{\mathit{ys}}$, it remains more than unity. Hence, the effectiveness of control system for laterally flexible asymmetric systems is more in reducing $u_{\mathit{yf}}$ as compared to corresponding symmetric systems. Further, for laterally flexible systems with Ω _θ = 1, the ratio, $R_t$ for $u_{\mathit{ys}}$ remains less than unity and for $u_{\mathit{yf}}$, it is more than unity except for laterally very flexible systems in which, reverse trend is observed. However, the variation in R _t is more significant and sensitive against the change in $T_y$ for torsionally flexible and strongly coupled systems and it is insensitive for torsionally stiff systems. Also, the ratio, $R_t$ for u _y and ${ü}_y$ remains almost near to the unity with the change in $T_y$. This implies that the difference between these responses of asymmetric and corresponding symmetric systems is very less and hence the effects of torsional coupling and asymmetry are negligible for responses at CM. Furthermore, from the second set of rows of Figure 14, it is observed that for the considered range of $T_y$ for systems with ${\Omega }_{\theta }$= 0.5 and 1, $R_t$ for ${ü}_{\mathit{ys}}$ remains more than unity and increases continuously with increase in $T_y$ and for ${ü}_{\mathit{yf}}$, the ratio remains less than unity and decreases continuously with increase in $T_y$. On the other hand, for the system with ${\Omega }_{\theta }$= 2, for the considered values of T _y , ratio, $R_t$ for ü _ys and ${ü}_{\mathit{yf}}$ remains almost near to the unity. This shows that for laterally stiff systems, the difference between the edge accelerations of asymmetric and corresponding symmetric system is less and the difference increases with the increase in value of $T_y$. Thus, the effects of asymmetry are more for laterally flexible asymmetric systems for edge acceleration responses as compared to corresponding symmetric systems.

Figure 14

Effect of lateral time period on response ratio, R _t for various displacement and acceleration responses and damper forces.

Furthermore, the variations of $R_t$ for $F_{\mathit{ds}}$, $F_{\mathit{df}}$ and $F_{\mathit{dy}}$ against T _y are shown in third set of rows of Figure 14. It is observed that for laterally stiff to laterally flexible systems with ${\Omega }_{\theta }$ = 0.5, ratio, $R_t$ for F _ds remains slightly more than unity and for $F_{\mathit{df}}$, it remains slightly less than unity, whereas, an opposite trend is observed for torsionally stiff systems. Moreover, for laterally stiff systems with ${\Omega }_{\theta }$= 1, the ratio, $R_t$ for $F_{\mathit{ds}}$ remains slightly less than unity and for F _df , it remains slightly more than unity, whereas, an opposite trend is observed for laterally flexible systems with ${\Omega }_{\theta }$= 1. However, the ratio, $R_t$ for resultant damper force, $F_{\mathit{dy}}$ remains almost equal to unity corresponding to all values of $T_y$ for ${\Omega }_{\theta }$ = 0.5, 1 and 2 with NLVDs. This implies that the damper force for controlled asymmetric building is almost same as the corresponding symmetric systems with NLVDs.

Further, from Figures 13 and 14, it is observed that the trends for the variation of $R_t$ for various displacement and acceleration responses as well as for damper forces obtained with LVDs are similar to those obtained with NLVDs. However, the variations in values of R _t for various responses as well as for damper forces are much more predominant and sensitive to the change in $e_x/r$ and $T_y$ for the systems installed with LVDs as compared to NLVDs. Further, the values of R _t obtained with NLVDs are much closer to unity as compared to the corresponding values obtained with LVDs. Thus, the difference between the displacement and accelerations responses and control forces of asymmetric and corresponding symmetric system is less for NLVDs as compared to LVDs and hence, the effects of torsional couplings are less for asymmetric system as compared to the corresponding symmetric systems for the systems installed with NLVDs in comparison to systems with LVDs.

Conclusions

The seismic response of linearly elastic, single-storey, one-way asymmetric building with LVDs and NLVDs subjected to different earthquake ground motions is investigated. The response is evaluated with parametric variations to study the comparative performance of LVDs and NLVDs for asymmetric system and the influence of important parameters on the effectiveness of control system for asymmetric systems. The important parameters considered are: eccentricity ratio of superstructure, uncoupled lateral time period, ratio of uncoupled torsional to lateral frequency and supplemental damping eccentricity ratio. From the trend of the results of the present study, the following conclusions can be drawn:

• 1. The difference between the resultant damper force of NLVDs and LVDs is more for torsionally stiff system as compared to torsionally flexible and strongly coupled systems.

• 2. The increase in supplemental damping ratio increases the effectiveness of dampers in reducing torsional displacement and accelerations, stiff edge displacement and accelerations as well as flexible edge displacements for systems with ${\Omega }_{\theta }$ = 0.5, 1 and 2. On the other hand, the effectiveness decreases for higher supplemental damping ratio in reducing flexible edge accelerations for systems with ${\Omega }_{\theta }$ = 0.5 and 1. Further, resultant damper force of NLVDs is less than the corresponding force of LVDs in the initial range of supplemental damping ratio (up to 30%) and for higher values of damping ratio, the reverse trend is observed.

• 3. The effectiveness of NLVDs is more sensitive to the eccentricity ratio for acceleration responses as compared to displacement responses. This phenomenon is more predominant for torsionally flexible and strongly coupled systems.

• 4. The effectiveness of dampers decreases with increase in lateral flexibility of building and effectiveness of NLVDs is more in reducing displacement responses as compared to accelerations. Further, NLVDs are more effective than LVDs for laterally flexible to stiff systems with ${\Omega }_{\theta }$= 0.5, 1 and 2 in reducing various displacement responses. On the other hand, the comparative performance of LVDs and NLVDs may vary depending on the value of ${\Omega }_{\theta }$ and T _y for reducing acceleration responses.

• 5. The difference between resultant damper force in NLVDs and corresponding force in LVDs strongly depends on structural eccentricity for torsionally flexible and strongly coupled systems as compared to torsionally stiff systems. Also, for laterally stiff systems ($T_y$ < 0.75 s), damper force for NLVDs is more than corresponding force of LVDs. On the other hand, for laterally flexible systems ($T_y$ > 0.75 s), reverse trend is observed and as the lateral flexibility of building increases, the difference between damper force of NLVDs and LVDs decreases.

• 6. The symmetric arrangement of dampers leads to higher reduction in torsional responses for building with intermediate eccentricity. For laterally stiff systems, location of CD on the same side of CR leads to higher reduction in stiff edge displacement and acceleration and CD is on the opposite side of CR leads to the higher reduction in flexible edge displacement and acceleration. In order to achieve this, CD should be as far as way from CM. For laterally flexible systems, CD on same side of CR and near to CM, leads to higher reduction in edge accelerations, whereas, locating CD at the extreme distance from CM on the side of CR leads to higher reduction in stiff edge displacement and opposite for flexible edge displacement.

• 7. The effects of torsional coupling are more pronounced for torsionally flexible and strongly coupled systems as compared to torsionally stiff systems while estimating the effectiveness of control system for asymmetric systems in reducing edge displacements and edge accelerations as compared to the corresponding symmetric systems.

• 8. The effects of asymmetry are more for laterally flexible asymmetric systems for edge acceleration responses as compared to corresponding symmetric systems.

• 9. The difference between the displacement and accelerations responses and control forces of asymmetric and corresponding symmetric system is less for NLVDs as compared to LVDs and hence, the effects of torsional couplings are less for asymmetric system as compared to the corresponding symmetric systems for the systems installed with NLVDs in comparison to system with LVDs.