Introduction

The asymmetry in buildings may be due to the uneven distribution of mass and/or stiffness of the structural members. In the past, many such asymmetric buildings have got severe damage during the seismic events. To prevent such damage, the eccentricity which is produced due to irregular distribution of mass and/or stiffness should be avoided. However, it may not be possible all the times to avoid the eccentricity due to stringent architectural and functional requirements, hence in such cases, the use of energy dissipation devices shall be beneficial to minimize the lateral–torsional responses.

In the past, many researchers have investigated the performance of base isolation, passive controls and active controls for asymmetric buildings. Hejal and Chopra (1989) studied the effects of lateral–torsional couplings and found that the response of building depends on structural eccentricity and frequency ratio. Jangid and Datta (1994) found that the effectiveness of base isolation reduces for higher eccentricity for torsionally coupled system. Jangid and Datta (1997) investigated that the effectiveness of multiple tuned mass dampers is overestimated by ignoring the system asymmetry. Goel (1998) investigated that the edge deformations in asymmetric-plan systems can be reduced than those in the corresponding symmetric systems by implementing proper supplemental damping. Date and Jangid (2001) carried out the study for asymmetric system with active control system and found that the effectiveness is overestimated by ignoring the effects of torsional coupling. Lin and Chopra (2003) investigated the effectiveness of non-linear viscous and visco-elastic dampers and concluded that the asymmetric distribution of damping reduces the response more effectively as compared to the symmetric distribution. De La Llera et al. (2005) proposed the weak torsional balance condition for system installed with friction dampers such as to minimize the correlation between translation and rotation. Matsagar and Jangid (2005) investigated the effects of torsional coupling on seismic response of base-isolated buildings and observed that for torsionally flexible system, the displacement response is more than that in case of the torsionally rigid system. Petti and De Iuliis (2008) proposed a method to optimally locate the viscous dampers for torsional response control in asymmetric-plan systems. Matsagar and Jangid (2010) studied the seismic response of asymmetric base-isolated structure during impact with adjacent structures and without impact. It was found that the torsionally coupled response becomes adverse with increasing eccentricities. Mevada and Jangid (2012a) investigated the performance of linear and non-linear viscous dampers for asymmetric systems and found that the effects of torsional coupling are less for asymmetric systems with non-linear dampers as compared to linear dampers.

Moreover, some of the researchers have studied the effects of semi-active control systems for asymmetric buildings in the recent past. Chi et al. (2000) investigated the performance of base isolation and semi-active magneto-rheological (MR) damper in asymmetric building and found them very effective for controlling the lateral–torsional responses. Yoshida et al. (2003) investigated the effectiveness of semi-active MR damper to control the torsional response of asymmetric building and concluded that the asymmetry leads to an increase in torsional response and decrease in translational response. Shook et al. (2009) studied the effectiveness of semi-active MR damper with fuzzy logic controller and found that it is effective in reducing the displacement and acceleration responses. Li and Li (2009) investigated the effectiveness of MR damper based on semi-geometric model for asymmetric building and found a greater reduction in displacement and acceleration responses compared to passive control case. Mevada and Jangid (2012b) investigated the seismic response of asymmetric building installed with semi-active variable dampers. It was observed that for torsionally flexible and strongly coupled systems, the effects of torsional coupling are more pronounced as compared to torsionally stiff systems. Mevada and Jangid (2012c) studied the effects of torsional coupling for asymmetric building installed with semi-active MR dampers and found that the effects of torsional coupling on effectiveness of semi-active MR damper system are more sensitive to the variation of eccentricity and torsional to lateral frequency ratio. Although, above studies reflect the effectiveness of passive and some of the semi-active systems in controlling the lateral–torsional responses, however, no specific study has been done to investigate the effectiveness of semi-active stiffness dampers for asymmetric buildings. Also, a comparative study to investigate the performance of passive stiffness and semi-active stiffness dampers for torsionally coupled building has not been done so far. Further, the effects of torsional coupling on the effectiveness of passive and semi-active stiffness dampers for the asymmetric systems are also not studied.

In this paper, the seismic response of single-storey, one-way asymmetric building is investigated under various earthquake ground motions. The objectives of the study are summarized as (i) to investigate the comparative seismic response of asymmetric building installed with passive stiffness damper (PSD) and two types of semi-active variable stiffness dampers (SAVSDs) namely, switching semi-active stiffness damper (SSASD) and resetting semi-active stiffness damper (RSASD) in controlling lateral, torsional and edge displacements as well as accelerations, and (ii) to study the effects of torsional coupling on the effectiveness of passive and semi-active variable stiffness dampers for asymmetric building as compared to the corresponding symmetric building. The important parameters considered are eccentricity ratio of superstructure, uncoupled time period and ratio of uncoupled torsional to lateral frequency.

Structural model and solution of equations of motion

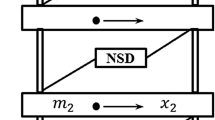
The system considered is an idealized single-storey building which consists of a rigid deck supported on columns as shown in Fig. 1. Following assumptions are made for the structural system under consideration: (i) floor of the superstructure is assumed as rigid, (ii) force–deformation behaviour of the superstructure is considered as linear and within elastic range (iii) the structure is excited by uni-directional horizontal component of earthquake ground motion and the vertical component of earthquake motion is neglected, and (iv) mass of the columns is ignored and the columns are considered to only provide lateral stiffness. The mass of deck is assumed to be uniformly distributed and hence centre of mass (CM) coincides with the geometrical centre of the deck. The columns are arranged in a way such that it produces the stiffness asymmetry with respect to the CM in one direction and hence, the centre of rigidity (CR) is located at an eccentric distance, e x from CM in x-direction. The system is symmetric in x-direction and therefore, two degrees of freedom are considered for model namely the lateral displacement in y-direction, u y and torsional displacement, \( u_{\uptheta} \) as represented in Fig. 1. The governing equations of motion of the building with lateral and torsional degrees of freedom are obtained by assuming that the control forces provided by the dampers are adequate to keep the response of the structure in the linear range. The equations of motion of the system in the matrix form are expressed as

Fig. 1
figure 1

Plan and isometric view of one-way asymmetric building showing arrangement of dampers

Full size image
$$ M{\ddot{\boldsymbol{u}}} + C\dot{u} + Ku = - M{\varvec{\Gamma}}{\ddot{\boldsymbol{u}}}_{g} + {\varvec{\Lambda}}\varvec{F,} $$
(1)

where M, C and K are mass, damping and stiffness matrices of the system, respectively; \( \varvec{u} = \left\{ {u_{y} \, u_{\uptheta} } \right\}^{\text{T}} \) is the displacement vector; Γ is the influence coefficient matrix; \( \varvec{{\ddot{\boldsymbol{u}}}}_{\varvec{g}} = \left\{ {{\ddot{\boldsymbol{u}}}_{gy} \, 0} \right\}^{\text{T}} \) is the ground acceleration vector; \( {\ddot{\boldsymbol{u}}}_{gy} \) is the ground acceleration in y-direction; Λ is the matrix that defines the location of control devices and \( \varvec{F} = \left\{ {F_{dy} \, F_{{d\uptheta}} } \right\}^{\text{T}} \) is the vector of control forces; and F dy and \( F_{{d\uptheta}} \) are resultant control forces of dampers along y- and \( \uptheta \)-direction, respectively.

The mass matrix can be expressed as:

$$ \varvec{M} = \left[ {\begin{array}{*{20}c} m & \text{0} \\ \text{0} & {mr^{2} } \\ \end{array} } \right] , $$
(2)

where m represents the lumped mass of the deck; and r is the mass radius of gyration about the vertical axis through CM which is given by, \( r = \sqrt {\left( {a^{2} + b^{2} } \right)/\text{12}} \); where a and b are the plan dimensions of the building.

The stiffness matrix of the system is obtained as follows,

$$ \varvec{K} = K_{y} \left[ {\begin{array}{*{20}c} \text{1} & {e_{x} } \\ {e_{x} } & {e_{x}^{2} + r^{2}\Omega _{\uptheta}^{2} } \\ \end{array} } \right] $$
(3)
$$ e_{x} = \frac{\text{1}}{{K_{y} }}\sum\limits_{i} {K_{yi} x_{i} } $$
(4)
$$ \Omega _{\uptheta} \text{ = }\frac{{\upomega_{\uptheta} }}{{\upomega_{y} }} $$
(5)
$$ \omega_{\theta } = \sqrt {\frac{{K_{\theta r} }}{{mr^{2} }}} \quad\text{and}\quad\omega_{y} = \sqrt {\frac{{K_{y} }}{m}} $$
(6)
$$ K_{\theta r} = K_{\theta \theta } - e_{x}^{2} K_{y} \quad \text{and} \quad K_{\theta \theta } = \sum\limits_{i} {K_{xi} y_{i}^{2} } + \sum\limits_{i} {K_{yi} x_{i}^{2} } , $$
(7)

where K y denotes the total lateral stiffness of the building in y-direction; e x is the structural eccentricity between CM and CR of the system; \( \Omega _{\uptheta} \) is the ratio of uncoupled torsional to lateral frequency of the system; K yi indicates the lateral stiffness of ith column in y-direction; x i is the x-coordinate distance of ith column with respect to CM; \( \upomega_{y} \) is uncoupled lateral frequency of the system; \( \upomega_{\uptheta} \) is uncoupled torsional frequency of the system; \( K_{\theta r} \) is torsional stiffness of the system about a vertical axis at the CR; \( K_{{\uptheta \uptheta }} \) is torsional stiffness of the system about a vertical axis at the CM; K xi indicates the lateral stiffness of ith column in x-direction; and y i is the y-coordinate distance of ith column with respect to CM.

The damping matrix of the system is not known explicitly and it is constructed from the Rayleigh’s damping considering mass and stiffness proportional as,

$$ \varvec{C} = a_{\text{0}} \varvec{M} + a_{\text{1}} \varvec{K,} $$
(8)

in which \( a_{\text{0}} \) and \( a_{\text{1}} \) are the coefficients depending on damping ratio of two vibration modes. For the present study, 5 % damping is considered for both modes of vibration of system.

The governing equations of motion are solved using the state-space method (Hart and Wong 2000; Lu 2004) and rewritten as:

$$ {\dot{\varvec z}} = \varvec{Az} + \varvec{BF} + {\varvec{E}}{\ddot{\varvec{u}}}_{\varvec{g}}, $$
(9)

where \( {\varvec{z}} = \left\{ {\varvec{u}\;\;\dot{\varvec{u}}} \right\}^{{\text{T}}} \) is a state vector; \( \varvec{A} \) is the system matrix; \( \varvec{B} \) is the distribution matrix of control forces; and \( \varvec{E} \) is the distribution matrix of excitations. These matrices are expressed as,

$$ \varvec{A = }\left[ {\begin{array}{*{20}c} {\mathbf{0}} & \varvec{I} \\ {\mathcal{ - }\varvec{M}^{{\mathcal{ - }\text{1}}} \varvec{K}} & {\mathcal{ - }\varvec{M}^{{\mathcal{ - }\text{1}}} \varvec{C}} \\ \end{array} } \right];\;\;\varvec{B = }\left[ \begin{gathered} {\mathbf{0}} \hfill \\ \varvec{M}^{{\mathcal{ - }\text{1}}} {\varvec{\Lambda}} \hfill \\ \end{gathered} \right]\;\text{and}\;\;\varvec{E = }\mathcal{ - }\left[ \begin{gathered} {\mathbf{0}} \hfill \\ {\varvec{\Gamma}} \hfill \\ \end{gathered} \right], $$
(10)

in which \( \varvec{I} \) is the identity matrix.

While Eq. (9) is discretized in time domain and the excitation and control forces are assumed to be constant within any time interval, the solution may be written in an incremental form (Hart and Wong 2000; Lu 2004),

$$ \varvec{z}\text{[}k\text{ + 1]} = \varvec{A}_{\varvec{d}} \varvec{ z}\text{[}k\text{]}+\varvec{ B}_{\varvec{d}} \varvec{ F}\text{[}k\text{]}+\varvec{ E}_{\varvec{d}} \varvec{ {\ddot{\boldsymbol{u}}}}_{\varvec{g}} \text{[}k\text{],} $$
(11)

where k denotes the time step; and \( \varvec{A}_{\varvec{d}} = e^{{\varvec{A}\Delta t}} \) represents the discrete-time system matrix with \( \Delta t \) as the time interval. The constant coefficient matrices \( \varvec{B}_{\varvec{d}} \) and \( \varvec{E}_{\varvec{d}} \) are the discrete-time counterparts of the matrices \( \varvec{B } \) and \( \varvec{E} \) and can be written as

$$ \varvec{B}_{\varvec{d}} = \varvec{A}^{{\text{ - 1}}} \varvec{(A}_{\varvec{d}} \mathcal{ - }\varvec{I) B}\;\quad \text{and}\quad \;\varvec{E}_{\varvec{d}} = \varvec{A}^{{\mathcal{ - }\text{1}}} (\varvec{A}_{\varvec{d}} \mathcal{ - }\varvec{I}{\mathbf{)}}\varvec{ E}\varvec{.} $$
(12)

Model of damper and control laws

Semi-active stiffness control devices are utilized to modify the stiffness and thus the natural vibration characteristics of the structure to which they are attached. The system primarily controls the stiffness of a building to establish a non-resonant condition during earthquakes. The semi-active stiffness devices are engaged or released so as to include or not include, respectively, the stiffness of the bracing system of the structure. Normally, the device is composed of a hydraulic cylinder with a normally closed solenoid control valve inserted in the tube connecting the two cylinder chambers. The solenoid valve can either be on or off, thus opening or closing, respectively, the fluid flow path through the tube. When the valve is closed, the fluid cannot flow and effectively locks the beam to the braces below. In contrast, when the valve is open, the fluid flows freely and disengages the stiffness control devices. The system may be regarded as fail-safe in the sense that the interruption of power causes the semi-active stiffness devices to automatically engage, thus increasing the stiffness of the structure (Kamagata and Kobori 1994; Kobori et al. 1993; Yang et al. 1996).

In past, many researchers have investigated the seismic response of symmetric structures using stiffness dampers. The non-resonant-type control system called as active variable systems were proposed by Kamagata and Kobori (1994) and Kobori et al. (1993). This system produces a non-stationary, non-resonant condition during earthquakes which is achieved by altering the building’s stiffness based on the nature of the earthquake. Yang et al. (1996) proposed the control methods based on sliding mode control to control the response of building installed with active variable systems. The semi-active stiffness and damping control device which are capable of modifying stiffness and damping in a continuous manner is proposed by Nagarajaiah and Mate (1997). Yang et al. (2000) proposed a general resetting control law for semi-active stiffness dampers and compared the performance of resetting and switching control laws for seismic response of symmetric buildings. Nasu et al. (2001) described the non-resonant control algorithm for the active variable stiffness system and verification of effectiveness of this control system. Kori and Jangid (2007) modified the switching control law based on the feedback from the displacement response.

Figure 2 shows the schematic and mathematical model of stiffness damper. When the valve is closed, the damper serves as a stiffness element in which the stiffness (k f ) is provided by the bulk modulus of the fluid in the cylinder. When the valve is open, the piston is free to move and the damper provides only a small damping without stiffness. The effective stiffness of the device consists of damper stiffness (k f ) and bracing stiffness (k bs ) and it is given by Yang et al. (2000) as follows:

Fig. 2
figure 2

Schematic and mathematical model of semi-active variable stiffness damper (Yang et al. 2000)

Full size image
$$ k_{hi} \text{ = }\frac{{k_{fi} k_{bsi} }}{{\text{(}k_{fi} + k_{bsi} \text{)}}}. $$
(13)

Switching semi-active control law

This control law has been derived based on sliding mode control by Kamagata and Kobori (1994) and Yang et al. (1996). In this control, the valve of hydraulic damper is pulsed to open during a certain time interval and close during another time interval, which can be referred as switching semi-active stiffness damper (SSASD). When a valve of the ith damper is closed, the effective stiffness, k hi , is added to the storey unit and when a valve is open, the effective stiffness, k hi , is zero. When the valve is switched off from on, a certain amount of energy is taken out of the structural system and when it is on, energy is added to the structural system.

The control force of ith SSASD can be obtained as

$$ F_{di} = k_{hi} v_{si} u_{i} , $$
(14)

where k hi is the effective stiffness of ith damper; u i is the relative displacement at the location of ith damper; and v si is the switching parameter of ith damper which is based on the switching control law expressed as (Yang et al. 2000)

$$ v_{si} \text{(}t\text{) = }\left\{ \begin{gathered} 1 \quad \text{ if }u_{i} \dot{u}_{i} \ge \text{0} \hfill \\ 0 \quad \text{ otherwise} \hfill \\ \end{gathered} \right., $$
(15)

when \( v_{si} \text{(}t\text{)} \) = 1, indicates that the ith SSASD is locked (i.e. valve is closed) and \( v_{si} \text{(}t\text{)} \) = 0, indicates the ith SSASD is unlocked (i.e. valve is open).

Resetting semi-active control law

In this control, the valve of hydraulic damper is closed for most of the time. Hence, the energy is stored in the damper-bracing systems in the form of potential energy. At appropriate time instants, the valve is pulsed to open and close quickly. The position of the piston of damper at that moment is referred as resetting position, u ri , and energy is released during this stage. The hydraulic damper in resetting mode is referred as resetting semi-active stiffness damper (RSASD) (Yang et al. 2000). The control force of ith RSASD can be obtained as

$$ F_{di} = k_{hi} \text{(}u_{i} - u_{ri} \text{),} $$
(16)

where u ri is resetting position of ith damper. When the RSASD is reset (valve is pulsed to open and close), u ri  = u i . At that instant, the applied damper force is zero. Yang et al. (2000) derived a resetting control law considering the Lyapunov function V as follows:

$$ V = \text{0}\text{.5 }\varvec{u}^{T} \varvec{Ku} + \text{0}\text{.5 }\dot{\varvec{u}}^{T} \varvec{M\dot{u}} +\upalpha_{L} \varvec{u}^{T} \varvec{M\dot{u},} $$
(17)

where \( \upalpha_{L} \) is constant such that the Lyapunov function is positive definite as follows:

$$ \left[ {\begin{array}{*{20}c} \varvec{K} & {\upalpha_{L} \varvec{M}} \\ {\upalpha_{L} \varvec{M}} & \varvec{M} \\ \end{array} } \right] > \text{0}\text{.} $$
(18)

Based on this, by minimizing \( \dot{V} \), Yang et al. (2000) derived the resetting control law as follows:

$$ u_{ri} \; = \;u_{i} \;\text{when}\;\dot{u}_{i} +\upalpha_{L} u_{i} = \text{0}\text{.} $$
(19)

Passive control

In passive mode of control, the valve is either always open or always closed. When the valve is always closed, the switching parameter v si is always considered equal to unity and the damper force of passive stiffness damper (PSD) is calculated as expressed in Eq. (14).

Numerical study

The seismic response of linearly elastic, single-storey, one-way asymmetric building installed with passive stiffness dampers (PSDs) and semi-active variable stiffness dampers (SAVSDs) is investigated by numerical simulation study. Total two stiffness dampers (either passive or semi-active, one at each edge) are installed in building as shown in Fig. 1. The force–deformation behaviour of the superstructure with dampers is assumed as linear and within elastic range. The response quantities of interest are lateral and torsional displacements of the floor obtained at the CM (u y and \( u_{\uptheta} \)), displacements at stiff and flexible edges of the system (u ys and \( u_{yf} = u_{y} \pm b \, u_{\uptheta} /2 \)), lateral and torsional accelerations of the floor obtained at the CM (\( {\ddot{\boldsymbol{u}}}_{y} \) and \( {\ddot{\boldsymbol{u}}}_{\uptheta} \)), accelerations at stiff and flexible edges of the system (\( {\ddot{\boldsymbol{u}}}_{ys} \) and \( {\ddot{\boldsymbol{u}}}_{yf} = {\ddot{\boldsymbol{u}}}_{y} \pm b \, {\ddot{\boldsymbol{u}}}_{\uptheta} /2 \)) as well as control forces of dampers located at stiff edge (F ds ) and at flexible edge (F df ) of the building. The response is investigated under following parametric variations: structural eccentricity ratio (e x /r), uncoupled lateral time period of system (\( T_{y} = 2\pi /\upomega_{y} \)) and uncoupled torsional to lateral frequency ratio (\( \Omega _{\uptheta} =\upomega_{\uptheta} /\upomega_{y} \)). The peak responses are obtained corresponding to the system parameters which are listed above and variations are plotted for the four real earthquake ground motions namely, Imperial Valley (1940), Loma Prieta (1989), Northridge (1994) and Kobe (1995) as per the details summarized in Table 1. The time histories of the ground motions of the earthquakes are shown in Fig. 3. These considered earthquakes are most accurately recorded and are widely used by the researchers and they cover the range of all varieties of earthquakes and hence shall be helpful to lead to the generalized conclusions. Total seismic weight of building considered for the present study is W = 250 kN and the aspect ratio between plan dimensions is considered as unity. For the numerical study carried out herein, the MATLAB tool has been used to solve the equations of motion. To study the effectiveness of implemented control system, the response is expressed in terms of indices, R e and R t , defined as follows:

Table 1 Details of earthquake motions considered for the numerical study
Full size table
Fig. 3
figure 3

Earthquake ground motions considered for the study

Full size image
$$ R_{e} = \frac{\text{Peak response of controlled asymmetric system}}{\text{Peak response of corresponding uncontrolled system}} $$
(20)
$$ R_{t} = \frac{\text{Peak response of controlled asymmetric system}}{\text{Peak response of corresponding symmetric system}}. $$
(21)

The value of R e less than one indicates that the implemented control system is effective in reducing the responses. On the other hand, the value of R t reflects the effects of torsional coupling on the effectiveness of control system. The value of R t greater than one indicates that the response of controlled asymmetric system increases due to torsional coupling as compared to the corresponding symmetric system.

For the stiffness damper, the effective damper stiffness (k hi ) plays an important role while designing the control system. For the present study, the stiffness ratio, (k r ) is defined as follows

$$ k_{r} \text{ = }\frac{{k_{hi} }}{{k_{si} }}, $$
(22)

where k si is the storey stiffness.

To arrive at the optimum value of stiffness ratio (k r ), a parametric study is carried out for torsionally flexible (\( \Omega _{\uptheta} \) = 0.5), strongly coupled (\( \Omega _{\uptheta} \) = 1) and torsionally stiff (\( \Omega _{\uptheta} \) = 2) systems with lateral time period, T y  = 1 s, and intermediate eccentricity ratio, e x /r = 0.3, installed with RSASDs. The response ratio, R e , are obtained for various displacements and accelerations and plotted against k r (which is varied from 0 to 2) in Figs. 4, 5 and 6 for systems with \( \Omega _{\uptheta} \) = 0.5, 1 and 2, respectively. Initially, the constant \( \upalpha_{L} \) of resetting control law is considered as zero (Yang et al. 2000). It is observed from the individual trends of various earthquakes as well as from average trends (of four earthquakes) from Figs. 4, 5 and 6 that with the increase in k r , the ratio, R e , for various displacements (\( u_{\uptheta} \), u y , u ys and u yf ), decreases continuously. This implies that the control system is more effective in reducing displacement with higher values of k r . On the other hand, R e for various accelerations (\( {\ddot{\boldsymbol{u}}}_{\uptheta} \), \( {\ddot{\boldsymbol{u}}}_{y} \), \( {\ddot{\boldsymbol{u}}}_{ys} \) and \( {\ddot{\boldsymbol{u}}}_{yf} \)) decreases initially with increase in k r and then increases with further increase in k r . This implies that there exists an optimum range of stiffness ratio, k r , to achieve the optimum reduction in torsional, lateral and edge accelerations. It is to be noted that the similar trends are observed for other values of \( \Omega _{\uptheta} \) (i.e. =1 and 2) Moreover, the variation of normalized peak resultant damper force against ratio, k r , is also shown in Figs. 4, 5, and 6. The damper forces are normalized with the total weight of building, W. It is observed that for larger values of k r , the control forces developed in the dampers are more. Thus, for asymmetric buildings, the torsional, lateral and edge displacements decrease with the increase in stiffness ratio (i.e. ratio between effective damper stiffness to storey stiffness). On the other hand, there exists an optimum value of stiffness ratio for torsional, lateral and edge accelerations. Hence, to achieve the optimum compromise between reduction in various displacement and acceleration responses as well as damper capacity, the suitable value of stiffness ratio, k r , is considered as 0.5 for the present study.

Fig. 4
figure 4

Effect of stiffness ratio (k r ) on response ratio, R e , for various responses for system installed with RSASD (\( \Omega _{\uptheta} \) = 0.5)

Full size image
Fig. 5
figure 5

Effect of stiffness ratio (k r ) on response ratio, R e , for various responses for system installed with RSASD (\( \Omega _{\uptheta} \) = 1)

Full size image
Fig. 6
figure 6

Effect of stiffness ratio (k r ) on response ratio, R e , for various responses for system installed with RSASD (\( \Omega _{\uptheta} \) = 2)

Full size image

The constant \( \upalpha_{L} \) used for resetting control law also plays an important role in performance of control system. Figure 7 shows the variations of ratio, R e , for lateral–torsional displacements and accelerations against \( \upalpha_{L} \). Initially the constant \( \upalpha_{L} \) is considered as zero and varied as long as the check for Lyapunov function (given by Eqs. 17 and 18) holds good. For the considered structural model, the Lyapunov function does not hold good beyond the value of \( \upalpha_{L} \) = 5. It is observed from the Fig. 7 that the ratios, R e , for various responses mildly increase with increase in \( \upalpha_{L} \), in general. However, the variation of R e for \( u_{\uptheta} \) is little more sensitive to the change in \( \upalpha_{L} \). Thus, for the study carried out herein, the constant \( \upalpha_{L} \) is considered as zero which led to higher reduction in various responses for structural system under consideration.

Fig. 7
figure 7

Effect of parameter, \( \upalpha_{L} \) on response ratio, R e , for various responses

Full size image

Comparative performance of PSDs and SAVSDs

To study the comparative performance of passive stiffness damper and semi-active stiffness dampers, various responses are obtained for the system with T y  = 1 s, \( \Omega _{\uptheta} \) = 1 and e x /r = 0.3 by considering the optimum value of stiffness ratio. The controlled responses are obtained by considering three control strategies namely, passive damper (PSD), switching semi-active stiffness damper (SSASD), and resetting semi-active stiffness damper (RSASD). The time histories of various uncontrolled and controlled responses like torsional displacement (\( u_{\uptheta} \)) and lateral displacement at CM (u y ) as well as torsional acceleration (\( {\ddot{\boldsymbol{u}}}_{\uptheta} \)) and lateral acceleration at CM (\( {\ddot{\boldsymbol{u}}}_{y} \)) are obtained under Imperial Valley (1940) earthquake and plotted in Figs. 8 and 9, respectively. It can be observed from the time histories that the reduction in various lateral–torsional responses is significantly higher for the system installed with RSASDs as compared to SSASDs and PSDs. On the contrary, the installation of PSDs increases the accelerations as compared to that of uncontrolled system. This is due to the fact that passive stiffness dampers in the building may increase the stiffness of the building to great extent and hence accelerations are higher. The valve for PSD is always opened or closed and a damper behaves as a bracing. It is further observed that the RSASDs are more effective in reducing torsional displacement and accelerations as compared to their lateral components. It is to be noted that the similar results are obtained under other three earthquakes.

Fig. 8
figure 8

Time histories for various displacements for different control strategies under Imperial Valley, 1940 earthquake

Full size image
Fig. 9
figure 9

Time histories for various accelerations for different control strategies under Imperial Valley, 1940 earthquake

Full size image

To compare the effectiveness of various control strategies in reducing the peak responses, the ratios, R e , are obtained for peak values of various displacements and accelerations such as torsional displacement (\( u_{\uptheta} \)), lateral displacement at CM (u y ), stiff edge displacement (u ys ) and stiff edge displacement (u yf ) as well as torsional acceleration (\( {\ddot{\boldsymbol{u}}}_{\uptheta} \)), lateral acceleration at CM (\( {\ddot{\boldsymbol{u}}}_{y} \)), stiff edge acceleration (\( {\ddot{\boldsymbol{u}}}_{ys} \)), and flexible edge acceleration (\( {\ddot{\boldsymbol{u}}}_{yf} \)). The results are obtained for the system with T y  = 1 s, \( \Omega _{\uptheta} \) = 1 and e x /r = 0.3 for PSD, SSASD and RSASD under considered earthquakes and shown in Table 2. It is observed from Table 2 that ratios, R e , for torsional, lateral and edge displacements as well as their acceleration counterparts are more for PSD as compared to SSASD and RSASD implying the effectiveness of semi-active systems. It is further observed that R e for various accelerations responses for system installed with PSD is more than unity indicating that the passive dampers are not effective in reducing the accelerations. Moreover, the bold numbers in parentheses for the cases of SSASD and RSASD indicate the percentage reduction in response ratio, R e , as compared to passive case. It is noticed that nearly all numbers in bold letters are positive indicating that the higher reduction can be achieved with semi-active devices as compared to passive device. Furthermore, the percentage reduction for RSASD case is more as compared to SSASD. The last column of table represents the average values of percentage reduction. It can be observed from that the percentage reduction in ratio, R e . for RSASD case is significantly higher as compared to that of SSASD and PSD cases. This implies that RSASDs are quite effective in reducing lateral–torsional and edge responses. In addition, the last set of rows of Table 2 shows the normalized peak resultant damper force for each case. It is noticed that the control force developed for RSASD is less than the corresponding force for PSD. Thus, the resetting semi-active stiffness dampers (RSASDs) perform better in reducing lateral, torsional and edge displacement as well as acceleration responses as compared to switching semi-active stiffness dampers (SSASDs) and passive stiffness dampers (PSDs) for asymmetric building.

Table 2 Response ratio, R e , for peak responses for different control strategies (T y  = 1 s, \( \Omega _{\uptheta} \) = 1 and e x /r = 0.3)
Full size table

Figure 10 shows the typical hysteresis loops for normalized damper force–displacement for dampers located at stiff and flexible edges of the building installed with PSDs, SSASDs and RSASDs for T y  = 1 s, \( \Omega _{\uptheta} \) = 1 and e x /r = 0.3 under Imperial Valley, 1940 earthquake. It is observed from the hysteresis loops that the semi-active switching and resetting dampers are more effective than passive stiffness dampers. The similar trends are observed for other cases also. Figure 11 shows the time instants of switching and resetting positions of dampers which are located at stiff and flexible edges of the building under Imperial Valley, 1940 earthquake for the period of 10 s for the system with T y  = 1 s, \( \Omega _{\uptheta} \) = 1 and e x /r = 0.3.

Fig. 10
figure 10

Normalized damper force–displacement loops for dampers located at stiff and flexible edges for different control strategies under Imperial Valley, 1940 earthquake

Full size image
Fig. 11
figure 11

Control actions of switching and resetting dampers located at stiff and flexible edges under Imperial Valley, 1940 earthquake

Full size image

Effects of torsional coupling for system installed with PSDs and SAVSDs

The effects of torsional coupling also play an important role while designing the control system. To study this, the ratio, R t , (which is between the peak response of controlled asymmetric and corresponding symmetric system) is obtained for lateral and edge displacement as well as acceleration responses for the system with T y  = 1 s and \( \Omega _{\uptheta} \) = 0.5, 1 and 2 and plotted against e x /r in Figs. 12, 13 and 14, respectively. The values of eccentricity ratio, e x /r, are varied from 0 to 1. The first row of Fig. 12a represents the variations obtained with PSDs and the second row represents the variations obtained with RSASDs for torsionally flexible system (\( \Omega _{\uptheta} \) = 0.5). It can be observed from that the ratio, R t , for lateral displacement at CM (u y ) and edge displacements (u ys and u yf ) varies significantly with change in e x /r for the system installed with PSDs as compared to RSASD. Further, from the average trend, it is observed that the ratio, R t , for stiff edge displacement, u ys , decreases and remains less than unity with increase in e x /r. This indicates that the effectiveness of control system is more for asymmetric system in reducing u ys as compared to the corresponding symmetric system. Thus, the effectiveness will be underestimated by ignoring the effects of eccentricity. On the other hand, the opposite trend is observed for flexible edge displacement, u yf . Further, a little variation is observed in the values of ratio, R t , for the response, u y , corresponding to the change in e x /r. Moreover, the difference between the responses of edge displacements of asymmetric and corresponding symmetric system increases with increase in superstructure eccentricity.

Fig. 12
figure 12

Variation of response ratio, R t for various peak displacements and accelerations against eccentricity ratio for PSD and RSASD under various earthquakes (\( \Omega _{\uptheta} \) = 0.5)

Full size image
Fig. 13
figure 13

Variation of response ratio, R t , for various peak displacements and accelerations against eccentricity ratio for PSD and RSASD under various earthquakes (\( \Omega _{\uptheta} \) = 1)

Full size image
Fig. 14
figure 14

Variation of response ratio, R t , for various peak displacements and accelerations against eccentricity ratio for PSD and RSASD under various earthquakes (\( \Omega _{\uptheta} \) = 2)

Full size image

Furthermore, Fig. 12b represents the variations of ratio, R t , against e x /r for lateral and edge acceleration responses. It can be observed from that the ratio, R t , for lateral acceleration at CM (\( {\ddot{\boldsymbol{u}}}_{y} \)) and edge accelerations (\( {\ddot{\boldsymbol{u}}}_{ys} \) and \( {\ddot{\boldsymbol{u}}}_{yf} \)) varies significantly with change in e x /r for the system installed with PSDs as compared to RSASDs. The values of ratio, R t , for various responses remain near to the unity for the system installed with RSASDs as compared to the system installed with PSDs. This implies that the effects of torsional coupling ARE higher for the system installed with PSDs. The similar results and trends are also observed for strongly coupled system (\( \Omega _{\uptheta} \) = 1) and torsionally stiff system (\( \Omega _{\uptheta} \) = 2) as represented in Figs. 13, 14. It is further observed that the ratio, R t , for various displacement and acceleration responses varies greatly for the systems with \( \Omega _{\uptheta} \) = 0.5 and 1 as compared to system with \( \Omega _{\uptheta} \) = 2. Thus, the effects of torsional coupling are higher for torsionally flexible and strongly coupled systems as compared to torsionally stiff systems installed with passive and semi-active stiffness dampers. Thus, the difference between various displacement and acceleration responses of asymmetric and corresponding symmetric system is significantly higher for system installed with PSDs and comparatively very less for the system installed with RSASDs and the difference increases with increase in superstructure eccentricity. Hence, the effects of torsional coupling are very less for the system installed with RSASDs as compared to PSDs.

While designing the control system, the damper capacity is the key issue. Hence, to study the effects of torsional coupling on damper control forces, the variations of response ratio, R t , for normalized peak damper forces against eccentricity ratio for PSDs and RSASDs under various earthquakes are shown in Fig. 15 for the system with T y  = 1 s and \( \Omega _{\uptheta} \) = 1. From the figure, in general, it can be observed that the ratio, R t , for normalized stiff edge damper force (F ds /W), flexible edge damper force (F df /W) and resultant damper force (F dT /W) varies significantly with change in e x /r for the system installed with PSDs as compared to RSASDs. From the average trends, it can be observed that, the ratio, R t , for F ds decreases with increase in e x /r and remains less than unity and for F df , it increases and remains more than unity. Hence, by ignoring the effects of torsional coupling, control forces at stiff edge, F ds , will be overestimated and at flexible edge, F df , it will be underestimated as compared to the corresponding symmetric systems. Further, the resultant damper force, F Dt , remains slightly less than unity for the system installed with RSASDs. Hence, resultant damper force will be slightly overestimated by ignoring the asymmetry. Further, the values of ratio, R t , for control forces for system installed with RSASDs are close to the unity as compared to system installed with PSDs. Thus, the effects of torsional coupling on damper control forces are less for the asymmetric system installed with resetting semi-active stiffness dampers (RSASDs) as compared to system installed with passive stiffness dampers (PSDs). Further, the difference between the control forces of dampers for asymmetric systems as compared to those of corresponding symmetric systems is very less for the systems installed with semi-active dampers, whereas the difference is significant for systems installed with passive dampers.

Fig. 15
figure 15

Variation of response ratio, R t , for normalized peak damper forces against eccentricity ratio for PSD and RSASD under various earthquakes

Full size image

Conclusions

The seismic response of linearly elastic, single-storey, one-way asymmetric building installed with passive stiffness dampers (PSDs) and semi-active dampers namely, switching semi-active stiffness dampers (SSASDs), and resetting semi-active stiffness dampers (RSASDs), subjected to real earthquake ground motions is investigated. The lateral–torsional responses are obtained with important system parameters such as eccentricity ratio of superstructure, uncoupled lateral time period, and ratio of uncoupled torsional to lateral frequency. The comparative performance of passive and semi-active control systems is studied. Further, the effects of torsional couplings are also studied for torsionally flexible, strongly coupled, and torsionally stiff systems installed with passive and resetting semi-active stiffness dampers. From the present numerical study, the following conclusions can be drawn:

  1. 1.

    For asymmetric buildings, the torsional, lateral and edge displacements decrease with the increase in stiffness ratio (i.e. ratio between effective damper stiffness to storey stiffness). On the other hand, there exists an optimum value of stiffness ratio for torsional, lateral and edge accelerations.

  2. 2.

    The resetting semi-active stiffness dampers (RSASDs) perform better in reducing lateral, torsional and edge displacement as well as acceleration responses as compared to switching semi-active stiffness dampers (SSASDs) and passive stiffness dampers (PSDs) for asymmetric building.

  3. 3.

    The difference between various displacement and acceleration responses of asymmetric and corresponding symmetric system is significantly higher for system installed with PSDs and comparatively very less for the system installed with RSASDs and the difference increases with increase in superstructure eccentricity. Hence, the effects of torsional coupling are very less for the system installed with RSASDs as compared to PSDs.

  4. 4.

    The effects of torsional coupling on damper control forces are less for the asymmetric system installed with resetting semi-active stiffness dampers (RSASDs) as compared to system installed with passive stiffness dampers (PSDs). Further, the difference between the control forces of dampers for asymmetric systems as compared to those of corresponding symmetric systems is very less for the systems installed with semi-active dampers, whereas the difference is significant for systems installed with passive dampers.