Area and power efficient DCT architecture for image compression

Abstract

The discrete cosine transform (DCT) is one of the major components in image and video compression systems. The final output of these systems is interpreted by the human visual system (HVS), which is not perfect. The limited perception of human visualization allows the algorithm to be numerically approximate rather than exact. In this paper, we propose a new matrix for discrete cosine transform. The proposed 8 × 8 transformation matrix contains only zeros and ones which requires only adders, thus avoiding the need for multiplication and shift operations. The new class of transform requires only 12 additions, which highly reduces the computational complexity and achieves a performance in image compression that is comparable to that of the existing approximated DCT. Another important aspect of the proposed transform is that it provides an efficient area and power optimization while implementing in hardware. To ensure the versatility of the proposal and to further evaluate the performance and correctness of the structure in terms of speed, area, and power consumption, the model is implemented on Xilinx Virtex 7 field programmable gate array (FPGA) device and synthesized with Cadence® RTL Compiler® using UMC 90 nm standard cell library. The analysis obtained from the implementation indicates that the proposed structure is superior to the existing approximation techniques with a 30% reduction in power and 12% reduction in area.

1 Introduction

Discrete cosine transform (DCT)[1] has become one of the basic tools in signal and image processing; the popularity of which is mainly due to its good energy compaction properties. In particular, DCT is the best substitute for the Karhunen-Loeve Transform (KLT), which is considered to be statistically optimal for energy concentration[2, 3], whereas the discrete cosine transform is suboptimal. The KLT is data dependent and requires more computation compared to the DCT. Due to this fact, discrete cosine transform is the finest substitute for the KLT. Indeed, DCT has found applications in many image and video compression standard such as JPEG[4], MPEG-1[5], MPEG-2[6], H.261[7], H.263[8], and H.264/AVC[9, 10]. During the JPEG process, an image is divided into several 8 × 8 blocks and then the two-dimensional discrete cosine transform (2-D DCT) is applied for encoding each block. The two-dimensional DCT of order N × N is defined as

$$\begin{array}{ll}{T}_{\text{DCT}}\left(u,v\right)& =\alpha \left(u\right)\alpha \left(v\right)\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}X\left(i,j\right)cos\left[\frac{\pi \left(2i+1\right)u}{2N}\right]\\ cos\left[\frac{\pi \left(2j+1\right)v}{2N}\right]\text{for}0\le i,j,u,v\le N-1\end{array}$$

(1)

Where

$$\alpha \left(u\right)=\alpha \left(v\right)=\left\{\begin{array}{ll}\sqrt{\frac{1}{N}}& \text{for}u,v=0\\ \sqrt{\frac{2}{N}}& \mathrm{otherwise}\end{array}\right\}$$

In general, the floating point DCT decorrelates the data being transformed so that most of its energy is packed in the low-frequency region, which is best suited for well-known image compression techniques[11–15] but does not meet the requirements of very fast real-time compression applications. For this reason, there has been huge interest in finding fixed point multiplication-free DCT algorithms[16–32] that can be implemented as low power and area efficient digital circuits, thus useful for mobile imaging devices.

In this scenario, recently a large number of DCT approximations have been proposed. Approximated algorithms provide a meaningful estimation at low complexity of 8-point DCT. Cham[16] proposed the integer cosine transforms (ICT) using the principle of dyad symmetry. The performance of ICT is very close to that of DCT. Haweel[17] proposed a signed DCT (SDCT) by applying a signum function to the DCT matrix, which maintains the good de-correlation and power compaction properties of the DCT but requires 24 additions and is not orthogonal. Lengwehasatit and Ortega[18] suggested the two 8 × 8 transform matrices, one for the coarsest and another for the finest. Using these two matrices, a trade-off between speedup and accuracy in various bit ranges can be achieved. The coding performance shows that 73% reduction in complexity with only 0.2 dB degradation in peak signal-to-noise ratio (PSNR). Tran[13] proposed the family of 8 × 8 biorthogonal transforms called binDCT, which are approximates of the popular 8 × 8 DCT. The binDCT requires 31 additions and 14 shift operations with a coding gain ranging from 8.77 to 8.82 dB, and shows finer approximations to exact DCT and are suitable for VLSI implementation. Bouguezel et al. proposed a series of DCT approximation techniques[19–23] which have a trade-off between computational complexity and image compression performance. Cintra and Bayer[24] proposed an approximate DCT based on the round-off function which requires 22 additions with less blocking artifacts. Bouguezel et al.[23] proposed a low complexity parametric transform for image compression, which requires 18 additions and 2 multiplications. This computational complexity can be reduced by varying the parameter a. Usually, the parameter a is selected as a small integer in order to minimize the computational complexity. In Bouguezel et al.[23], the suggested values of a∊ {0, 1/2, 1}. For the value a = 1/2, the two multiplications become just bit-shift operations. If a = 1, then no shift operation is necessary. The transform requires only 18 additions. In the case of a = 0, the complexity reduces to 16 additions. Brahimi and Bouguezel[25] proposed an efficient fast integer DCT transform which is also claimed to require only 16 additions, and it is not orthogonal. Senapati et al.[26] proposed a low complexity orthogonal 8 × 8 transform matrix for fast image compression, which requires 14 additions and two shift operations. This computational complexity is further reduced by Bayer and Cintra[27] to 14 additions, which gives better image compression performance than the classic SDCT[17] and Bouguezel et al.[23] transforms. Cintra et al.[28] proposed a very low complexity DCT approximation obtained via pruning, which is claimed to require only 10 additions. However, the performance results reported in[28] is not reproduced, since the proposed work concentrates on non-pruned techniques. On the other hand, integrating multiple standard encoding or decoding hardware into a single chip increases the area and power consumption. Numerous architectures have proposed a low power, high speed and area efficient hardware implementation for DCT computation[32–35].

In general, DCT approximation with low computational complexity and low bit rates are preferred. In this paper, a low complexity multiplier-less DCT approximation is proposed, which is more essential for hardware realization. The derived fast algorithm requires only 12 additions, which is lesser than the number of additions required for any existing DCT approximation[17–27, 29–31]. To examine the performance and trade-offs associated with the algorithm, we have coded the proposed as well as the existing algorithms[17, 19, 21–24, 26, 27] in MATLAB and Verilog HDL, and it is synthesized with Xilinx Virtex 7 XC7V585T-2LFFG1761C device (Xilinx, Inc., San Jose, CA, USA)[36] and Cadence® RTL Compiler®[37] using UMC 90 nm standard cell library.

The rest of the paper is structured as follows. In Section 2, the proposed transform and the factors influencing its performance improvements and computational complexity are compared with the existing methods. An image compression simulation and hardware implementation for the proposed and existing approximation DCT are detailed and analyzed in Section 3. Conclusion and final remarks are given in Section 4.

2 Proposed transform

Haweel[17] introduces the approximation DCT method by applying the signum function operator to the DCT element in Equation 1. The T_SDCT is given by

$$T_{\text{SDCT}}\left(u,v\right)=\frac{1}{\sqrt{N}}\text{sign}\left\{T_{\text{DCT}}\left(u,v\right)\right\}$$

(2)

where sign T_DCT(u, v) = {.}, which is the signum function defined as follows:

$$\text{sign}\left\{x\right\}=\left\{\begin{array}{ccc}+1& \text{if}& x>0\\ 0& \text{if}& x=0\\ -1& \text{if}& x<0\end{array}\right.$$

(3)

Signed DCT has many advantages, one of which is apparent from looking at Equations 1 to 3 as all the elements in the transform are 0 or ±1, which eradicates the need of a multiplication operation or a transcendental expression. The transform order need not be a specific integer or a power of 2. The SDCT also maintains the periodicity and spectral structure of its originating DCT and in turn maintains good de-correlation and energy compaction characteristics. Therefore, SDCT is highly preferred for low computation applications.

There have been many recent approaches for reducing the computational complexity of the DCT transform, but the reduction in computational complexity comes at the cost of PSNR. In this paper, a new DCT approximation scheme is developed by reproducing the reported butterfly structures[17, 23, 26, 27]. After reviewing these structures, the common computations are identified and shared to remove the redundancy in DCT matrix and simulated using MATLAB tool. The image compression performance was evaluated based on the PSNR values, the matrix is altered and the procedure is repeated. First, the transform matrix is reduced to 16 additions[29] and then to 14 additions[30] and to 12 additions. The forward and inverse transform matrices are obtained as follows:

$$T=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 1\\ 1& 1& 0& 0& 0& 0& 1& 1\\ 0& 0& 1& 0& 0& 1& 0& 0\\ 0& 0& 1& 1& 1& 1& 0& 0\\ 0& 0& 1& 1& -1& -1& 0& 0\\ 0& 0& 1& 0& 0& -1& 0& 0\\ 1& 1& 0& 0& 0& 0& -1& -1\\ 1& 0& 0& 0& 0& 0& 0& -1\end{array}\right]$$

(4)

$$T^{-1}=\left[\begin{array}{cccccccc}1& 0& 0& 0& 1& 0& 0& 0\\ -1& 1& 0& 0& -1& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 1& 0\\ 0& 0& -1& 1& 0& 0& -1& 1\\ 0& 0& -1& 1& 0& 0& 1& -1\\ 0& 0& 1& 0& 0& 0& -1& 0\\ -1& 1& 0& 0& 1& -1& 0& 0\\ 1& 0& 0& 0& -1& 0& 0& 0\end{array}\right]*D$$

(5)

where$D=\mathrm{diag}\left(1,1,1,1,1,1,1,1\right)*\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right..$

It can be seen from Equations 4 and 5 that the entries of T and T^-1 are {0, ±1}. This indicates that the proposed transform requires only 12 additions, thus avoiding the need for multiplication and bit shift operations. In terms of complexity assessment, the diagonal matrix D may not introduce any computational overhead. In JPEG, the DCT operation is a preprocessing step for a subsequent coefficient quantization procedure. Consequently, the scaling factors in the diagonal matrix D can be merged to the de-quantization matrix. This procedure is clearly suggested and adopted in several works[19–27].

The number of additions in the proposed transform can be clearly understood from the butterfly diagram shown in Figure 1. Input data x_n, where n = 0,1,2,…7, is related to the output X_k, where k = 0,1,2,…7. The continuous and dashed line represents multiplication by +1 and -1 respectively. The common use of additions is reduced without disturbing PSNR in considerable levels. The number of additions, multiplications, and bit-shift operations required for the proposed transform and the evolution of SDCT is presented in Table 1. This clearly shows that the proposed matrix has 14.29%, 25%, 33.3%, and 50% saving in computation than Bayer and Cintra[27], Senapati et al.[26] Bouguezel et al.[23], and SDCT[17], respectively.

Figure 1

Signal flow graph for the proposed transform of order N = 8.

Table 1 Arithmetic computation complexity assessment

3 Experimental results and analysis

3.1. Application to image compression

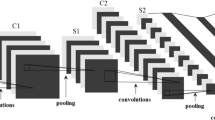
To evaluate the performance of the proposed transform matrix in image compression, we used the experimental methodology described in[17] and it was supported by[18–27] as shown in Figure 2. A set of 30 512 × 512 8-bit grayscale images obtained from a standard public image bank[39] were considered, which were grouped into three image types. For example, Lena, Cameraman, Goldhill, and Boat are low-frequency (LF) images; Barbara and House are medium frequency (MF) images; and Mandrill and Grass are high frequency (HF) images. The proposed fast DCT and existing transforms[17, 19, 21–24, 26, 27] have been implemented in MATLAB and the performance parameters such as PSNR and compression ratio (CR) are determined.

Figure 2

Implementation of proposed transform matrix in image coding.

A simulation has been carried out for the proposed and existing approximated discrete cosine transforms by incorporating the international standard lossy image compression algorithm produced by a joint photographic expert group, which employs the DCT. Each image is divided into non-overlapping blocks of 8 × 8 pixels. The pixel values in the original block are converted from the unsigned integer format to signed integer format, and then an approximate DCT is applied. After the transform coefficients are quantized, less significant coefficients are set to zero and rearranged into the standard zigzag sequence, only r out of the 64 transform coefficients in each block is employed to reconstruct the image. The inverse procedure was applied to reconstruct the processed data and image.

The transform matrices of the so far evolved SDCT are used to evaluate and position the performance of the proposed transform. The original and reconstructed images using the proposed and existing methods are illustrated, and the PSNR comparisons are presented in Table 2 and Figure 3. It is clear from Table 2 that the PSNR obtained by the Bouguezel et al.[22] is significantly higher than the other recent algorithms, but it requires a greater number of arithmetic operations. This proposal concentrates on low computational complexity algorithms. We separate the Bouguezel et al.[23], Cintra and Bayer[24], Senapati et al.[26], and Bayer and Cintra[27] for further comparisons. Table 2 and Figure 3 show that the proposed transform has a better PSNR than Bouguezel et al.[23], Cintra and Bayer[24], Senapati et al.[26], and Bayer and Cintra[27] for almost all types of images. When compared to the methods such as Bayer and Cintra[27], Bouguezel et al.[23], and Senapati et al.[26] the proposed method outperforms these by 1.28, 2.56, and 2.01 dB improvement in the average PSNR and 1.30, 2.59, and 1.88 dB improvement in the peak PSNR, respectively.

Table 2 PSNR obtained by different 8 × 8 transform matrices

Figure 3

Reconstructed with proposed transform, Bayer and Cintra [27] and Bouguezel et al. [23]. For (a) Lena, (b) Boat, (c) Barbara, and (d) Airplane images.

Further, to show the efficiency of the proposed transform matrix in image compression, the PSNR is obtained by varying the number of transform coefficients retained in steps of four to reconstruct the image. For the sake of reference, the DCT results are also included. Figure 4 shows that the proposed approximated transform is comparable when r < 32 and it outperforms when r ≥ 32 for all the types (LF, MF, and HF) of images. The overall results show that the proposed transform gives comparable or better image compression performance than the so far evolved SDCT. At the same time, it provides ample reduction in the number of arithmetic operations, which is more essential for hardware realization.

Figure 4

PSNR obtained by different transforms. (a) Lena, (b) Cameraman, (c) Barbara, and (d) Mandrill images.

3.2. Hardware implementation

In this section, the performance of the proposed and the existing DCT matrices are compared in terms of hardware cost and computing time. The digital architecture of the proposed approximate DCT is shown in Figure 5. The hardware cost is measured by the number of adders, multipliers, and shifters used in the architecture, and the computing time is normalized as clock cycles.

Figure 5

Digital architecture for proposed approximate DCT.

3.2.1 Field programmable gate array implementation

The proposed approximation DCT matrix and the reported matrices[17, 19, 21–24, 26, 27] were physically implemented on a Xilinx Virtex 7 XC7V585T-2LFFG1761C device[36]. The inputs were assumed at an 8-bit resolution and are realized with pipelining in order to increase the throughput. To get the accurate timing result, post-place and route (PAR) is done for each run of the design flow. Since the hardware resource requirements become low for the proposed method, it gains greater flexibility in placement and routing to get the optimized delay. The implementation is evaluated in terms of hardware complexity, time delay, and area consumption. The resource utilization (area) is measured as the numbers of the cell usage (input/output buffers and global clock buffers) and lookup tables (LUTs). The resources used by the implementation are listed in Table 3. It is observed from Table 3 that the proposed structure has area utilization (No. of LUTs) of 13.72%, 35.29%, and 29% lesser as compared to Bayer and Cintra[27], Bouguezel et al.[23], and Senapati et al.[26], respectively.

Table 3 Comparison of hardware resource consumption with the reported architectures on Xilinx Virtex-7 XC7V585T-2LFFG1761C device

3.2.2 ASIC implementation

The field programmable gate array (FPGA) verified register transfer language (RTL) code was targeted to UMC 90 nm standard cell library using Cadence encounter® RTL complier[37]. The supply voltage of the CMOS was fixed at V_DD = 1 V during the estimation of area and power consumption. The design was realized up to the synthesis and place and route levels leading to the estimated results tabulated in Table 4. Table 4 shows that the Bayer and Cintra[27] transform consumes lesser area among the existing structures. We can say that the proposed structure consumes 12% lesser area and offers 30% power optimization with 9% reduction in critical path delay compared to the Bayer and Cintra[27].

Table 4 Comparison of hardware resource consumption with the reported architectures for CMOS 90 nm ASIC implementation

4 Conclusions

Low power and area minimization are the two indispensable requirements for portable multimedia devices, which employs various signal and image processing algorithms. In this paper, we proposed a new 8 × 8 transformation matrix, which requires only 12 additions, thus avoiding the need for multiplication and bit shift operations. The proposed approximation DCT for image compression is a simple, efficient architecture having lower computational complexity with improvement in the peak signal-to-noise ratio. According to the results, the proposed transform has a comparable or better image compression performance than the Bouguezel et al.[23], Cintra and Bayer[24], Senapati et al.[26], and Bayer and Cintra[27] transforms. When compared to the most recent method of Bayer and Cintra[27] transform, the proposed method outperforms it by a 1.28 dB improvement in the average PSNR and a 1.30 dB improvement in the peak PSNR, while providing 14% reduction in the number of arithmetic operations. Further, the efficiency of the proposed transform which was implemented on Xilinx Virtex 7 device and was later synthesized with Cadence RTL complier using UMC 90 nm standard cell library has been determined. It has been found to have 30% reduction in power and 12% reduction in area when compared to the existing approximation transform Bayer and Cintra[27]. The implementation that has been carried out in this work clearly shows that the architecture is best suited for real-time low power and high speed applications.