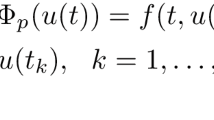Eigenvalue criteria for existence of positive solutions of impulsive differential equations with non-separated boundary conditions

Abstract

In this paper, we discuss the existence of positive solutions for second-order differential equations subject to nonlinear impulsive conditions and non-separated periodic boundary value conditions. Our criteria for the existence of positive solutions will be expressed in terms of the first eigenvalue of the corresponding nonimpulsive problem. The main tool of study is a fixed point theorem in a cone.

MSC:34B37, 34B18.

1 Introduction

Let ω be a fixed positive number. In this paper, we are concerned with the existence of positive solutions for the following boundary value problem (BVP) with impulses:

(1.1a)

(1.1b)

(1.1c)

Here, $u^{[1]}(t)=p(t)u^{\prime }(t)$ denotes the quasi-derivative of $u(t)$. The condition (1.1c) is called a non-separated periodic boundary value condition for (1.1a).

We assume throughout, and with further mention, that the following conditions hold.

(H1) Let $J=[0,\omega ]$, and $0<t_1<t_2<\cdots <t_m<\omega$, $f\in C(J\times R^{+},R^{+})$, $I_i\in C(R^{+},R^{+})$, $R^{+}=[0,+\mathrm{\infty })$. $\mathrm{\Delta }(u^{[1]}(t_i))=u^{[1]}(t_i^{+})-u^{[1]}(t_i^{-})$, where $u^{[1]}(t_i^{+})$ (respectively $u^{[1]}(t_i^{-})$) denotes the right limit (respectively, the left limit) of $u^{[1]}(t)$ at $t=t_i$.

• (H)
  $$\begin{array}{c}{\int }_0^{\omega }\frac{1}{p(t)}dt<\mathrm{\infty },{\int }_0^{\omega }q(t)dt<\mathrm{\infty },\hfill \\ p>0,q\ge 0\text{ and }q\not\equiv 0\text{ a.e. on }[0,\omega ].\hfill \end{array}$$

A function $u(t)$ defined on $J^{-}=J\mathrm{\setminus }\{t_1,t_2,\dots ,t_m\}$ is called a solution of BVP (1.1) ((1.1a)-(1.1c)) if its first derivative $u^{\prime }(t)$ exists for each $t\in J^{-}$, $p(t)u^{\prime }(t)$ is absolutely continuous on each close subinterval of $J^{-}$, there exist finite values $u^{[1]}(t_i^{\pm })$, the impulse conditions (1.1b) and the boundary conditions (1.1c) are satisfied, and the equation (1.1a) is satisfied almost everywhere on $J^{-}$.

For the case of $I_i=0$ ($i=1,2,\dots ,m$), the problem (1.1) is related to a non-separated periodic boundary value problem of ODE. Atici and Guseinov [1] have proved the existence of a positive and twin positive solutions to BVP (1.1) by applying a fixed point theorem for the completely continuous operators in cones. In [2], Graef and Kong studied the following periodic boundary value problem:

$$\{\begin{array}{c}-{(p(t)u^{\prime })}^{\prime }+q(t)u=h(t)f(t,u),t\in (0,\omega ),\hfill \\ u(0)=u(\omega ),u^{[1]}(0)=u^{[1]}(\omega ),\hfill \end{array}$$

(1.2)

where $h(t)>0$. Based upon the properties of Green’s function obtained in [1], the authors extended and improved the work of [1] by using topological degree theory. They derived new criteria for the existence of non-trivial solutions, positive solutions and negative solutions of the problem (1.2) when f is a sign-changing function and not necessarily bounded from below even over $[0,\omega ]\times R^{+}$. Very recently, He et al. [3] studied BVP (1.1) without impulses and generalized the results of [1, 4] via the fixed point index theory. The problem (1.2) in the case of $p\equiv 1$, the usual periodic boundary value problem, has been extensively investigated; see [4–7] for some results.

On the other hand, impulsive differential equations are a basic tool to study processes that are subjected to abrupt changes in their state. There has been a significant development in the last two decades. Boundary problems of second-order differential equations with impulse have received considerable attention and much literature has been published; see, for instance, [8–17] and their references. However, there are fewer results about positive solutions for second-order impulsive differential equations. To our best knowledge, there is no result about nonlinear impulsive differential equations with non-separated periodic boundary conditions.

Motivated by the work above, in this paper we study the existence of positive solutions for the boundary value problem (1.1). By using fixed point theorems in a cone, criteria are established under some conditions on $f(t,u)$ concerning the first eigenvalue corresponding to the relevant linear operator. More important, the impulsive terms are different from those of papers [8, 9].

2 Preliminaries

In this section, we collect some preliminary results that will be used in the subsequent section. We denote by $\phi (t)$ and $\psi (t)$ the unique solutions of the corresponding homogeneous equation

$$-{(p(t)u^{\prime }(t))}^{\prime }+q(t)u(t)=0,t\in J,$$

(2.1)

under the initial boundary conditions

$$\phi (0)=1,{\phi }^{[1]}(0)=0;\psi (0)=0,{\psi }^{[1]}(0)=1.$$

(2.2)

Put $D=\phi (\omega )+{\psi }^{[1]}(\omega )-2$, then by [[1], Lemma 2.3], $D>0$.

Definition 2.1 For two differential functions y and z, we define their Wronskian by

$$W_t(y,z)=y(t)z^{[1]}(t)-y^{[1]}(t)z(t)=p(t)[y(t)z^{\prime }(t)-y^{\prime }(t)z(t)].$$

Theorem 2.1 The Wronskian of any two solutions for equations (2.1) is constant. Especially, $W_t(\phi ,\psi )\equiv 1$.

Proof Suppose that y and z are two solutions of (2.1), then

$$\begin{array}{rcl}{\{W_t(y,z)\}}^{\prime }& =& {\{p(t)[y(t)z^{\prime }(t)-y^{\prime }(t)z(t)]\}}^{\prime }\\ =& y(t){[p(t)z^{\prime }(t)]}^{\prime }-{[p(t)y^{\prime }(t)]}^{\prime }z(t)=0;\end{array}$$

therefore, the Wronskian is constant. Further, from the initial conditions (2.2), we have $W_t(\phi ,\psi )\equiv 1$. The proof is complete. □

Consider the following equation:

$$\{\begin{array}{c}-{(p(t)u^{\prime }(t))}^{\prime }+q(t)u(t)=0,t\in J,\hfill \\ u(0)=u(\omega ),u^{[1]}(0)=u^{[1]}(\omega ).\hfill \end{array}$$

(2.3)

From Theorem 2.5 in [1], equation (2.3) has a Green function $G(t,s)>0$ for all $s,t\in J$, which has the following properties:

($G_1$) $G(t,s)$ is continuous in t and s for all $t,s\in J$.

($G_2$) If $A={min}_{0\le t,s\le \omega }G(t,s)$ and $B={max}_{0\le t,s\le \omega }G(t,s)$, then $B>A>0$.

($G_3$)

$$\begin{array}{rcl}G(t,s)& =& \frac{\psi (\omega )}{D}\phi (t)\phi (s)-\frac{{\phi }^{[1]}(\omega )}{D}\psi (t)\psi (s)\\ +\{\begin{array}{cc}\frac{{\psi }^{[1]}(\omega )-1}{D}\phi (t)\psi (s)-\frac{\phi (\omega )-1}{D}\phi (s)\psi (t),\hfill & 0\le s\le t\le \omega ,\hfill \\ \frac{{\psi }^{[1]}(\omega )-1}{D}\phi (s)\psi (t)-\frac{\phi (\omega )-1}{D}\phi (t)\psi (s),\hfill & 0\le t\le s\le \omega .\hfill \end{array}\end{array}$$

Combining with Theorem 2.1, we can also prove that

($G_4$)

$$G(0,s)=G(\omega ,s),p(t)\frac{\partial G}{\partial t}{|}_{(0,s)}=p(t)\frac{\partial G}{\partial t}{|}_{(\omega ,s)},{\int }_0^{\omega }q(t)G(t,s)ds=1.$$

Remark 1 From paper [1], we can get $G(t,s)$ when $q(t)=\frac{c^2}{p(t)}$ ($c>0$) and $p(t)>0$,

$$\begin{array}{c}G(t,s)=\frac{1}{2c({\mathrm{e}}^{c{\int }_0^{\omega }(dx/p(x))}-1)}\{\begin{array}{cc}{\mathrm{e}}^{c{\int }_s^t(dx/p(x))}+{\mathrm{e}}^{c[{\int }_0^{\omega }(dx/p(x))+{\int }_t^s(dx/p(x))]},\hfill & 0\le s\le t\le \omega ,\hfill \\ {\mathrm{e}}^{c{\int }_t^s(dx/p(x))}+{\mathrm{e}}^{c[{\int }_0^{\omega }(dx/p(x))+{\int }_s^t(dx/p(x))]},\hfill & 0\le t\le s\le \omega ,\hfill \end{array}\hfill \\ A=\frac{{\mathrm{e}}^{c/2{\int }_0^{\omega }(dx/p(x))}}{c[{\mathrm{e}}^{c{\int }_0^{\omega }(dx/p(x))}-1]},B=\frac{1+{\mathrm{e}}^{c{\int }_0^{\omega }(dx/p(x))}}{2c[{\mathrm{e}}^{c{\int }_0^{\omega }(dx/p(x))}-1]}.\hfill \end{array}$$

Especially, in the case of $p(t)\equiv 1$, $q(t)\equiv c^2$ ($c>0$), Green’s function $G(t,s)$ has the form

$$\begin{array}{c}G(t,s)=\frac{1}{2c({\mathrm{e}}^{c\omega }-1)}\{\begin{array}{cc}{\mathrm{e}}^{c(t-s)}+{\mathrm{e}}^{c(\omega +s-t)},\hfill & 0\le s\le t\le \omega ,\hfill \\ {\mathrm{e}}^{c(s-t)}+{\mathrm{e}}^{c(\omega +t-s)},\hfill & 0\le t\le s\le \omega ,\hfill \end{array}\hfill \\ A=\frac{{\mathrm{e}}^{(c\omega /2)}}{c({\mathrm{e}}^{c\omega }-1)},B=\frac{1+{\mathrm{e}}^{c\omega }}{2c({\mathrm{e}}^{c\omega }-1)}.\hfill \end{array}$$

Define an operator

$$(Tu)(t)={\int }_0^{\omega }G(t,s)u(s)ds,$$

then it is easy to check that $T:C(J)\to C(J)$ is a completely continuous operator. By virtue of the Krein-Rutman theorem, the authors in [3] got the following result.

Lemma 2.1 The spectral radius $r(T)>0$ and T has a positive eigenfunction corresponding to its first eigenvalue ${\lambda }_1={(r(T))}^{-1}$.

In what follows, we denote the positive eigenfunction corresponding to ${\lambda }_1$ by ϕ and ${max}_{t\in J}\varphi (t)=1$. Define a mapping Φ and a cone K in a Banach space $C(J)$ by

$$\begin{array}{c}(\mathrm{\Phi }u)(t)=\lambda {\int }_0^{\omega }G(t,s)f(s,u(s))ds+\sum _{i=1}^{m}G(t,t_i)I_i(u(t_i)),t\in J,\hfill \\ K=\{u\in C(J),u(t)\ge \delta \parallel u\parallel \},\hfill \end{array}$$

where $\delta =\frac{A}{B}$, $\parallel u\parallel ={max}_{t\in J}|u(t)|$.

Lemma 2.2 The fixed point of the mapping Φ is a solution of (1.1).

Proof Clearly, Φu is continuous in t. For $t\ne t_k$,

$${(\mathrm{\Phi }u)}^{\prime }(t)=\lambda {\int }_0^{\omega }\frac{\partial G}{\partial t}f(s,u(s))ds+\sum _{i=1}^m\frac{\partial G}{\partial t}(t,t_i)I_i(u(t_i)).$$

Using ($G_3$) and ($G_4$), we have $(\mathrm{\Phi }u)(0)=(\mathrm{\Phi }u)(\omega )$, ${(\mathrm{\Phi }u)}^{[1]}(0)={(\mathrm{\Phi }u)}^{[1]}(\omega )$ and

which implies that the fixed point of Φ is the solution of (1.1). The proof is complete. □

The proofs of the main theorems of this paper are based on fixed point theory. The following two well-known lemmas in [18] are needed in our argument.

Lemma 2.3 [18]

Let X be a Banach space and K be a cone in X. Suppose ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ are open subsets of X such that $0\in {\mathrm{\Omega }}_1\subset {\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$, and suppose that

$$\mathrm{\Phi }:K\cap ({\overline{\mathrm{\Omega }}}_2\mathrm{\setminus }{\mathrm{\Omega }}_1)\to K$$

is a completely continuous operator such that

• ${inf}_{u\in K\cap \partial {\mathrm{\Omega }}_1}\parallel \mathrm{\Phi }u\parallel >0$, $u\ne \mu \mathrm{\Phi }u$for$u\in K\cap \partial {\mathrm{\Omega }}_1$and$\mu \ge 1$, and$u\ne \mu \mathrm{\Phi }u$for$u\in K\cap \partial {\mathrm{\Omega }}_2$and$0<\mu \le 1$, or

• ${inf}_{u\in K\cap \partial {\mathrm{\Omega }}_2}\parallel \mathrm{\Phi }u\parallel >0$, $u\ne \mu \mathrm{\Phi }u$for$u\in K\cap \partial {\mathrm{\Omega }}_2$and$\mu \ge 1$, and$u\ne \mu \mathrm{\Phi }u$for$u\in K\cap \partial {\mathrm{\Omega }}_1$and$0<\mu \le 1$.

Then Φ has a fixed point in $K\cap ({\overline{\mathrm{\Omega }}}_2\mathrm{\setminus }{\mathrm{\Omega }}_1)$.

Lemma 2.4 [18]

Let X be a Banach space and K be a cone in X. Suppose ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ are open subsets of X such that $0\in {\mathrm{\Omega }}_1\subset {\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$, and suppose that

$$\mathrm{\Phi }:K\cap ({\overline{\mathrm{\Omega }}}_2\mathrm{\setminus }{\mathrm{\Omega }}_1)\to K$$

is a completely continuous operator such that

• There exists$u_0\in K\mathrm{\setminus }\{0\}$such that$u\ne \mathrm{\Phi }u+\mu u_0$for$u\in K\cap \partial {\mathrm{\Omega }}_1$and$\mu >0$, $\parallel \mathrm{\Phi }u\parallel \le \parallel u\parallel$for$u\in K\cap \partial {\mathrm{\Omega }}_2$, or

• There exists$u_0\in K\mathrm{\setminus }\{0\}$such that$u\ne \mathrm{\Phi }u+\mu u_0$for$u\in K\cap \partial {\mathrm{\Omega }}_2$and$\mu >0$, $\parallel \mathrm{\Phi }u\parallel \le \parallel u\parallel$for$u\in K\cap \partial {\mathrm{\Omega }}_1$.

Then Φ has a fixed point in ${\overline{\mathrm{\Omega }}}_2\mathrm{\setminus }{\mathrm{\Omega }}_1$.

3 Main results

Recalling that δ was defined after Lemma 2.1, for convenience, we introduce the following notations. Assume that the constant $r>0$ and γ is some positive function on J,

$$\begin{array}{c}{\overline{f}}_{\gamma }^r=sup\{\frac{f(t,u)}{\gamma (t)u},t\in J,u\in [\delta r,r]\},\hfill \\ f_{\gamma }^r=inf\{\frac{f(t,u)}{\gamma (t)u},t\in J,u\in [\delta r,r]\},\hfill \\ {\overline{f}}_{\gamma }^0=\underset{r\to 0^{+}}{lim}{\overline{f}}_{\gamma }^r,f_{\gamma }^0=\underset{r\to 0^{+}}{lim}{f}_{\gamma }^r,{\overline{f}}_{\gamma }^{\mathrm{\infty }}=\underset{r\to +\mathrm{\infty }}{lim}{\overline{f}}_{\gamma }^r,f_{\gamma }^{\mathrm{\infty }}=\underset{r\to +\mathrm{\infty }}{lim}{f}_{\gamma }^r,\hfill \\ {\overline{I}}_i^r=sup\{\frac{I_i(u)}{u},u\in [\delta r,r]\},I_i^r=inf\{\frac{I_i(u)}{u},u\in [\delta r,r]\},\hfill \\ {\overline{I}}_i^0=\underset{r\to 0^{+}}{lim}{\overline{I}}_i^r,I_i^0=\underset{r\to 0^{+}}{lim}{I}_i^r,{\overline{I}}_i^{\mathrm{\infty }}=\underset{r\to +\mathrm{\infty }}{lim}{\overline{I}}_i^r,I_i^{\mathrm{\infty }}=\underset{r\to +\mathrm{\infty }}{lim}{I}_i^r.\hfill \end{array}$$

Theorem 3.1 Assume that there exist positive constants α, β such that $f_q^{\alpha }\ge 0$, ${\overline{f}}_q^{\beta }\ge 0$, $I_i^{\alpha }\ge 0$, $I_i^{\beta }\ge 0$ and

$$0<\lambda \in (\frac{1-A{\sum }_{i=1}^m{I}_i^{\alpha }}{f_q^{\alpha }},\frac{1-B{\sum }_{i=1}^m{\overline{I}}_i^{\beta }}{{\overline{f}}_q^{\beta }}).$$

(3.1)

Then (1.1) has at least one positive solution u such that $min\{\alpha ,\beta \}\le \parallel u\parallel \le max\{\alpha ,\beta \}$.

Proof Clearly, $\alpha \ne \beta$, let $\alpha =min\{\alpha ,\beta \}$, $\beta =max\{\alpha ,\beta \}$. Define the open sets

$${\mathrm{\Omega }}_{\alpha }=\{u\in C(J):\parallel u\parallel <\alpha \},{\mathrm{\Omega }}_{\beta }=\{u\in C(J):\parallel u\parallel <\beta \}.$$

Then $\mathrm{\Phi }:K\cap ({\overline{\mathrm{\Omega }}}_{\beta }\mathrm{\setminus }{\mathrm{\Omega }}_{\alpha })$ is completely continuous. By (3.1) and the definition of $f_q^{\alpha }$, $I_i^{\alpha }$, ${\overline{f}}_q^{\beta }$, ${\overline{I}}_i^{\beta }$, there exists $\epsilon >0$ such that

(3.2)

(3.3)

and

$$f(t,u)\le (1+\epsilon ){\overline{f}}_q^{\beta }q(t)u,I_i(u)\le (1+\epsilon ){\overline{I}}_i^{\beta }u,i=1,2,\dots ,m,\delta \beta \le u\le \beta .$$

(3.4)

Let $u_0\equiv 1$. We show that

$$u\ne \mathrm{\Phi }u+\mu ,\mathrm{\forall }u\in K\cap \partial {\mathrm{\Omega }}_{\alpha }\text{ and }\mu >0.$$

(3.5)

If not, there exist $u_1\in K\cap \partial {\mathrm{\Omega }}_{\alpha }$ and ${\mu }_1>0$ such that $u_1=\mathrm{\Phi }{u}_1+{\mu }_1$. Let $u_1(\rho )={min}_{t\in J}{u}_1(t)$. Noting that $\delta \alpha \le u_1\le \alpha$ for any $t\in J$, we obtain that for $t\in J$,

$$\begin{array}{rcl}{u}_1(t)& =& (\mathrm{\Phi }{u}_1)(t)+{\mu }_1\\ =& \lambda {\int }_0^{\omega }G(t,s)f(s,u_1(s))ds+\sum _{i=1}^{m}G(t,t_i)I_i(u_1(t_i))+{\mu }_1\\ \ge & (1-\epsilon )\lambda f_q^{\alpha }{\int }_0^{\omega }G(t,s)q(s)u_1(s)ds+A(1-\epsilon )\sum _{i=1}^m{I}_i^{\alpha }{u}_1(t_i)+{\mu }_1\\ \ge & (1-\epsilon )\lambda f_q^{\alpha }{u}_1(\rho ){\int }_0^{\omega }G(t,s)q(s)ds+A{u}_1(\rho )(1-\epsilon )\sum _{i=1}^m{I}_i^{\alpha }+{\mu }_1\\ \ge & (1-\epsilon )(\lambda f_q^{\alpha }+A\sum _{i=1}^m{I}_i^{\alpha })u_1(\rho )+{\mu }_1\\ \ge & u_1(\rho )+{\mu }_1,\end{array}$$

which implies that $u_1(\rho )>u_1(\rho )$, a contradiction.

On the other hand, for $\mathrm{\forall }u\in K\cap \partial {\mathrm{\Omega }}_{\beta }$, $\delta \beta \le u(t)\le \beta$, we have

$$\begin{array}{rcl}(\mathrm{\Phi }u)(t)& =& \lambda {\int }_0^{\omega }G(t,s)f(s,u(s))ds+\sum _{i=0}^{m}G(t,t_i)I_i(u_i(t))\\ \le & (1+\epsilon )\lambda {\overline{f}}_q^{\beta }{\int }_0^{\omega }G(t,s)q(s)u(s)ds+B(1+\epsilon )\sum _{i=1}^m{\overline{I}}_i^{\beta }u(t_i)\\ \le & (1+\epsilon )\lambda {\overline{f}}_q^{\beta }\parallel u\parallel {\int }_0^{\omega }G(t,s)q(s)ds+B(1+\epsilon )\parallel u\parallel \sum _{i=1}^m{\overline{I}}_i^{\beta }\\ \le & (1+\epsilon )(\lambda {\overline{f}}_q^{\beta }+B\sum _{i=1}^m{\overline{I}}_i^{\beta })\parallel u\parallel \le \parallel u\parallel .\end{array}$$

From Lemma 2.4 it follows that Φ has a fixed point $u\in K\cap ({\overline{\mathrm{\Omega }}}_{\beta }\mathrm{\setminus }{\mathrm{\Omega }}_{\alpha })$. Furthermore, $\alpha \le \parallel u\parallel \le \beta$ and $u(t)\ge \delta \alpha >0$, which means that $u(t)$ is a positive solution of Eq. (1.1). The proof is complete. □

In the next theorem, we make use of the eigenvalue ${\lambda }_1$ and the corresponding eigenfunction ϕ introduced in Lemma 2.1.

Theorem 3.2 Assume that there exist positive constants α, β such that $f_{\gamma }^{\alpha }\ge 0$, $f_{\gamma }^{\beta }\ge 0$, $I_i^{\alpha }\ge 0$, $I_i^{\beta }\ge 0$ and

$$0<\lambda \in (\frac{{\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{I}_i^{\alpha }\varphi (t_i)}{\delta f_{\gamma }^{\alpha }{\int }_0^{\omega }\varphi (s)ds},\frac{\delta {\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{\overline{I}}_i^{\beta }\varphi (t_i)}{\delta {\overline{f}}_{\gamma }^{\beta }{\int }_0^{\omega }\varphi (s)ds}),$$

(3.6)

here $\gamma \equiv 1$ on J. Then (1.1) has at least one positive solution u such that $min\{\alpha ,\beta \}\le \parallel u\parallel \le max\{\alpha ,\beta \}$.

Proof Obviously, $\alpha \ne \beta$, put $\alpha =min\{\alpha ,\beta \}$, $\beta =max\{\alpha ,\beta \}$. Define the open sets

$${\mathrm{\Omega }}_{\alpha }=\{u\in C(J):\parallel u\parallel <\alpha \},{\mathrm{\Omega }}_{\beta }=\{u\in C(J):\parallel u\parallel <\beta \}.$$

At first, we show that $\mathrm{\Phi }:K\cap ({\overline{\mathrm{\Omega }}}_{\beta }\mathrm{\setminus }{\mathrm{\Omega }}_{\alpha })\to K$. For any $u\in K\cap ({\overline{\mathrm{\Omega }}}_{\beta }\mathrm{\setminus }{\mathrm{\Omega }}_{\alpha })$, from ($G_2$), we have

$$0<(\mathrm{\Phi }u)(t)\le B(\lambda {\int }_0^{\omega }f(s,u(s))ds+\sum _{i=1}^m{I}_i(u(t_i)))<\mathrm{\infty }.$$

On the other hand,

$$(\mathrm{\Phi }u)(t)\ge A(\lambda {\int }_0^{\omega }f(s,u(s))ds+\sum _{i=1}^m{I}_i(u(t_i)))\ge \frac{A}{B}\parallel \mathrm{\Phi }u\parallel .$$

It is easy to check that $\mathrm{\Phi }:K\cap ({\overline{\mathrm{\Omega }}}_{\beta }\mathrm{\setminus }{\mathrm{\Omega }}_{\alpha })\to K$ is completely continuous.

Next, we show that

$$\mu \mathrm{\Phi }u\ne u,\mathrm{\forall }u\in K\cap \partial {\mathrm{\Omega }}_{\beta }\text{ and }0<\mu \le 1.$$

(3.7)

If not, there exist ${\mu }_0\in (0,1]$ and $u_0\in K\cap \partial {\mathrm{\Omega }}_{\beta }$ such that ${\mu }_0\mathrm{\Phi }{u}_0=u_0$. Hence,

$$\{\begin{array}{c}-{(p(t)u_0^{\prime }(t))}^{\prime }+q(t)u_0(t)={\mu }_0\lambda f(t,u_0(t)),t\in J^{-},\hfill \\ -\mathrm{\Delta }(u_0^{[1]}(t_k))={\mu }_0{I}_k(u_0(t_k)),k=1,\dots ,m,\hfill \\ u_0(0)=u_0(\omega ),u_0^{[1]}(0)=u_0^{[1]}(\omega ).\hfill \end{array}$$

(3.8)

Multiplying the first equation of (3.8) by ϕ and integrating from 0 to ω, we obtain that

$$-{\int }_0^{\omega }{(p(t)u_0^{\prime }(t))}^{\prime }\varphi (t)dt+{\int }_0^{\omega }q(t)u_0(t)\varphi (t)dt={\mu }_0\lambda {\int }_0^{\omega }f(s,u_0(s))\varphi (s)ds.$$

(3.9)

One can find that

$${\int }_0^{\omega }{(p(t)u_0^{\prime }(t))}^{\prime }\varphi (t)dt={\mu }_0\sum _{i=1}^m{I}_i(u_0(t_i))\varphi (t_i)+{\int }_0^{\omega }(q(t)-{\lambda }_1)\varphi (t)u_0(t)dt.$$

(3.10)

Substituting (3.10) into (3.9), we get

$$-{\mu }_0\sum _{i=1}^m{I}_i(u_0(t_i))\varphi (t_i)+{\lambda }_1{\int }_0^{\omega }\varphi (t)u_0(t)dt={\mu }_0\lambda {\int }_0^{\omega }f(t,u_0(t))\varphi (t)dt.$$

Noting that $\delta \parallel u_0\parallel \le u_0\le \parallel u_0\parallel$, therefore,

$$-\parallel u_0\parallel \sum _{i=1}^m{\overline{I}}_i^{\beta }\varphi (t_i)+{\lambda }_1\delta \parallel u_0\parallel {\int }_0^{\omega }\varphi (t)dt\le \lambda {\overline{f}}_{\gamma }^{\beta }{\int }_0^{\omega }\varphi (t)dt\parallel u_0\parallel ,$$

which implies that

$$\lambda \ge \frac{\delta {\lambda }_1{\int }_0^{\omega }\varphi (s)ds-{\sum }_{i=1}^m{\overline{I}}_i^{\beta }\varphi (t_i)}{{\overline{f}}_{\gamma }^{\beta }{\int }_0^{\omega }\varphi (s)ds},$$

a contradiction.

Finally, we show that

$$\underset{u\in K\cap \partial {\mathrm{\Omega }}_{\alpha }}{inf}\parallel \mathrm{\Phi }u\parallel >0,\mu \mathrm{\Phi }u\ne u,\mathrm{\forall }u\in K\cap \partial {\mathrm{\Omega }}_{\alpha }\text{ and }\mu \ge 1.$$

Since $f(t,u)$ and $I_i(u)$ are negative for $u\in [\delta \alpha ,\alpha ]$ and $t\in J$, the condition (3.6) implies that $f_{\gamma }^{\alpha }>0$. Hence, ${\int }_0^{\omega }f(s,u(s))ds>0$ for $u\in K\cap \partial {\mathrm{\Omega }}_{\alpha }$ and for any $u\in K\cap \partial {\mathrm{\Omega }}_{\alpha }$,

$$\begin{array}{rcl}(\mathrm{\Phi }u)(t)& =& \lambda {\int }_0^{\omega }G(t,s)f(s,u(s))ds+\sum _{i=1}^{m}G(t,t_i)I_i(u(t_i))\\ \ge & A\lambda {\int }_0^{\omega }f(s,u(s))ds>0.\end{array}$$

Suppose that there exist ${\mu }_0\ge 1$ and $u_0\in K\cap \partial {\mathrm{\Omega }}_{\alpha }$ such that ${\mu }_0\mathrm{\Phi }{u}_0=u_0$, that is,

$$\{\begin{array}{c}-{(p(t)u_0^{\prime }(t))}^{\prime }+q(t)u_0(t)={\mu }_0\lambda f(t,u_0(t)),t\in J^{-},\hfill \\ -\mathrm{\Delta }(u_0^{[1]}(t_k))={\mu }_0{I}_k(u_0(t_k)),k=1,\dots ,m,\hfill \\ u_0(0)=u_0(\omega ),u_0^{[1]}(0)=u_0^{[1]}(\omega ).\hfill \end{array}$$

(3.11)

Multiplying the first equation of (3.11) by ϕ and integrating from 0 to ω, we obtain that

$$-{\int }_0^{\omega }{(p(t)u_0^{\prime }(t))}^{\prime }\varphi (t)dt+{\int }_0^{\omega }q(t)u_0(t)\varphi (t)dt={\mu }_0\lambda {\int }_0^{\omega }f(s,u_0(s))\varphi (s)ds.$$

(3.12)

One can get that

$$\begin{array}{rcl}{\int }_0^{\omega }{(p(t)u_0^{\prime }(t))}^{\prime }\varphi (t)dt& =& {\mu }_0\sum _{i=1}^m{I}_i(u_0(t_i))\varphi (t_i)+{\int }_0^{\omega }{(p(t){\varphi }^{\prime }(t))}^{\prime }{u}_0(t)dt\\ =& {\mu }_0\sum _{i=1}^m{I}_i(u_0(t_i))\varphi (t_i)+{\int }_0^{\omega }(q(t)-{\lambda }_1)\varphi (t)u_0(t)dt.\end{array}$$

(3.13)

Substituting (3.13) into (3.12), we get

$$-{\mu }_0\sum _{i=1}^m{I}_i(u_0(t_i))\varphi (t_i)+{\lambda }_1{\int }_0^{\omega }\varphi (t)u_0(t)dt={\mu }_0\lambda {\int }_0^{\omega }f(t,u_0(t))\varphi (t)dt.$$

Noting that $\delta \parallel u_0\parallel \le u_0\le \parallel u_0\parallel$, therefore,

$$\begin{array}{rcl}-\delta \parallel u_0\parallel \sum _{i=1}^m{I}_i^{\alpha }\varphi (t_i)+{\lambda }_1\parallel u_0\parallel {\int }_0^{\omega }\varphi (t)dt& \ge & {\mu }_0\lambda {\int }_0^{\omega }f(s,u_0(s))ds\\ \ge & \lambda \delta f_{\gamma }^{\alpha }{\int }_0^{\omega }{u}_0(s)\varphi (s)ds\\ \ge & \lambda \delta f_{\gamma }^{\alpha }{\int }_0^{\omega }\varphi (s)ds\parallel u_0\parallel >0.\end{array}$$

It is impossible for ${\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{I}_i^{\alpha }\varphi (t_i)\le 0$. When ${\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{I}_i^{\alpha }\varphi (t_i)>0$,

$$\lambda <\frac{{\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{I}_i^{\alpha }\varphi (t_i)}{\delta f_{\gamma }^{\alpha }{\int }_0^{\omega }\varphi (s)ds},$$

a contradiction.

From Lemma 2.3 it follows that Φ has a fixed point $u\in K\cap ({\overline{\mathrm{\Omega }}}_{\beta }\mathrm{\setminus }{\mathrm{\Omega }}_{\alpha })$. Furthermore, $\alpha \le \parallel u\parallel \le \beta$ and $u\ge \delta \alpha >0$, which means that $u(t)$ is a positive solution of Eq. (1.1). The proof is complete. □

Corollary 3.1 Assume that $f_{\gamma }^0>0$, $f_{\gamma }^{\mathrm{\infty }}>0$, $I_i^0>0$, $I_i^{\mathrm{\infty }}>0$ and

$$0<\lambda \in (\frac{{\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{I}_i^0\varphi (t_i)}{\delta f_{\gamma }^0{\int }_0^{\omega }\varphi (s)ds},\frac{\delta {\lambda }_1{\int }_0^{\omega }\varphi (s)ds-{\sum }_{i=1}^m{\overline{I}}_i^{\mathrm{\infty }}\varphi (t_i)}{{\overline{f}}_{\gamma }^{\mathrm{\infty }}{\int }_0^{\omega }\varphi (s)ds})$$

or

$$0<\lambda \in (\frac{{\lambda }_1{\int }_0^{\omega }\varphi (s)ds-\delta {\sum }_{i=1}^m{I}_i^{\mathrm{\infty }}\varphi (t_i)}{\delta f_{\gamma }^{\mathrm{\infty }}{\int }_0^{\omega }\varphi (s)ds},\frac{\delta {\lambda }_1{\int }_0^{\omega }\varphi (s)ds-{\sum }_{i=1}^m{\overline{I}}_i^0\varphi (t_i)}{{\overline{f}}_{\gamma }^0{\int }_0^{\omega }\varphi (s)ds}),$$

here $\gamma \equiv 1$ on J. Then (1.1) has at least one positive solution.

Corollary 3.2 Assume that there exists a constant α such that $f_{\gamma }^{\rho }>0$, $I_i^{\rho }>0$ ($\rho =0$, α and ∞) and

$$\frac{{\overline{f}}_{\gamma }^{\alpha }{\int }_0^{\omega }\varphi (s)ds+{\sum }_{i=1}^m{\overline{I}}_i^{\alpha }\varphi (t_i)}{\delta {\int }_0^{\omega }\varphi (s)ds}<{\lambda }_1<min\{\delta f_{\gamma }^0+\frac{\delta {\sum }_{i=1}^m{I}_i^0\varphi (t_i)}{{\int }_0^{\omega }\varphi (s)ds},\delta f_{\gamma }^{\mathrm{\infty }}+\frac{\delta {\sum }_{i=1}^m{I}_i^{\mathrm{\infty }}\varphi (t_i)}{{\int }_0^{\omega }\varphi (s)ds}\},$$

here $\gamma \equiv 1$ on J. Then there exists one open interval $\mathrm{\Theta }:1\in \mathrm{\Theta }$ such that (1.1) has at least two positive solutions for $\lambda \in \mathrm{\Theta }$.

Example 1 Consider the equation

$$\{\begin{array}{c}-u^{″}(t)+3u(t)=\lambda f(t,u),t\in J,t\ne t_i,\hfill \\ -\mathrm{\Delta }{u}^{\prime }(t)=I_i(u(t_i)),i=1,2,\dots ,m,\hfill \\ u(0)=u(1),u^{\prime }(0)=u^{\prime }(1),\hfill \end{array}$$

(3.14)

where $p(t)=1$, $q(t)=3$ and

$$f(t,u)=\{\begin{array}{cc}{u}^{\rho },\hfill & u\le 1,\hfill \\ 1,\hfill & u>1,\hfill \end{array}{I}_i(u)=\{\begin{array}{cc}3,\hfill & u\le 1,\hfill \\ 3\sqrt{u},\hfill & u>1,\hfill \end{array}$$

here $\rho >1$ and $i=1,2,\dots ,m$. Since $I_i^0=+\mathrm{\infty }$, ${\overline{I}}_i^{\mathrm{\infty }}=0$ and ${\overline{f}}_q^{\mathrm{\infty }}=0$, by Theorem 3.1, (3.14) has at least one positive solution for any $\lambda >0$.

Example 2 Consider the equation

$$\{\begin{array}{c}-u^{″}(t)+20u(t)=\lambda f(t,u),t\in J,t\ne t_i,\hfill \\ -\mathrm{\Delta }{u}^{\prime }(t_i)=I_i(u(t_i)),i=1,2,\dots ,m,\hfill \\ u(0)=u(1),u^{\prime }(0)=u^{\prime }(1),\hfill \end{array}$$

(3.15)

where $f(t,u)=\frac{{\mathrm{e}}^{-u}}{10}$, $I_i(u)=\frac{u^2}{100(m+i)}$.

It is well known that, for the problem consisting of the equation $-u^{″}=\lambda u$, $t\in (0,1)$, and the boundary condition

$$u(0)=u(1),u^{\prime }(0)=u^{\prime }(1),$$

(3.16)

the first eigenvalue is 0 (see, for example, [[19], p.428]). It follows that the first eigenvalue is ${\lambda }_1=20$ for the problem consisting of the equation

$$-u^{″}+20u=\lambda u,t\in (0,1),$$

and the boundary condition (3.16). Meanwhile, we can obtain the positive eigenfunction $\varphi (t)\equiv 1$ corresponding to ${\lambda }_1$. It is also easy to check that $\delta =\frac{2\sqrt{\mathrm{e}}}{1+\mathrm{e}}$, $f_{\gamma }^0=+\mathrm{\infty }$, $f_{\gamma }^{\mathrm{\infty }}=0$ and $I_i^{\mathrm{\infty }}=+\mathrm{\infty }$ (here $\gamma =1$). So, the right-hand side of the inequality in Corollary 3.2 is obviously satisfied. Considering the monotonicity of $f(t,u)$ and $I_i$, we can choose a sufficiently small positive constant α such that the left-hand side of the inequality is true. Therefore, by a direct application of Corollary 3.2, there exists one open interval $\mathrm{\Theta }:1\in \mathrm{\Theta }$ such that (3.15) has at least two positive solutions for $\lambda \in \mathrm{\Theta }$.