Abstract
In this paper, the modified Kudryashov method is proposed to solve fractional differential equations, and Jumarie’s modified Riemann-Liouville derivative is used to convert nonlinear partial fractional differential equation to nonlinear ordinary differential equations. The modified Kudryashov method is applied to compute an approximation to the solutions of the space-time fractional modified Benjamin-Bona-Mahony equation and the space-time fractional potential Kadomtsev-Petviashvili equation. As a result, many analytical exact solutions are obtained including symmetrical Fibonacci function solutions, hyperbolic function solutions, and rational solutions. This method is powerful, efficient, and it can be used as an alternative to establish new solutions of different types of fractional differential equations applied in mathematical physics.
Similar content being viewed by others
1 Introduction
Nonlinear partial differential equations of integer order play an important role in describing many nonlinear phenomena such as mathematical biology, electromagnetic theory, fluid mechanics, signal processing, engineering, solid state physics, and other fields of science. With the help of computerized symbolic computations many researchers implemented various methods to establish the solutions to different nonlinear differential equations. For example, the Exp-function method [1–3], the Jacobi elliptic function expansion method [4, 5], the first integral method [6, 7], -expansion method [8, 9], the direct algebraic method [10], the Cole-Hopf transformation method [11], and others.
Nonlinear fractional differential equations (FDEs) are a generalization of classical differential equations of integer order. Recently, FDEs have attracted great interest, using the fractional derivatives. It is caused both by the development of the theory of fractional calculus itself and by the applications of such constructions in various real life problems. In the past decades the theory of fractional derivatives was represented principally as a pure theoretical field of mathematics effective only for mathematicians. However, in recent years many authors have noticed that derivatives of non-integer order are convenient for the description of the properties of various physical phenomena. It has been shown that fractional-order models are more sufficient than the formerly used integer-order models. Some physical considerations by means of the models based on derivatives of non-integer order are given in [12–15]. New exact solutions for fractional differential equations may help to understand better the corresponding wave phenomena they describe. In order to obtain the solutions for fractional differential equations, many numerical and analytical methods have been proposed so far (e.g. see [12–32]). But the application of a modified Kudryashov method to fractional differential equations has not been researched.
In this paper, we will apply the modified Kudryashov method for solving fractional partial differential equations in the sense of the modified Riemann-Liouville derivative as given by Jumarie [33, 34]. To illuminate the utility and validness of the method, we will apply it to the space-time fractional modified Benjamin-Bona-Mahony (mBBM) equation and the space-time fractional potential Kadomstev-Petviashvili (PKP) equation.
2 Preliminaries and the modified Kudryashov method
Jumarie’s modified Riemann-Liouville derivative is defined as
where
Moreover, some properties for the proposed modified Riemann-Liouville derivative are given in [34] as follows:
which are direct results of the equality , which holds for non-differentiable functions.
We present the main steps of the modified Kudryashov method as follows [35–39].
For given nonlinear FDEs for a function u of independent variables, :
where , , , and are the modified Riemann-Liouville derivatives of u with respect to t, x, y and z. P is a polynomial in and its various partial derivatives, in which the highest-order derivatives and nonlinear terms are involved.
Step 1. We investigate the traveling wave solutions of Eq. (2.6) of the form
where k, n, m and λ are arbitrary constants. Then Eq. (2.6) reduces to a nonlinear ordinary differential equation of the form
Step 2. We suppose that the exact solutions of Eq. (2.8) can be obtained in the following form:
where and the function Q is the solution of the equation
Step 3. According to the method, we assume that the solution of Eq. (2.8) can be expressed in the form
In the calculation of the value of N in Eq. (2.11) we have the pole order for the general solution of Eq. (2.8). In order to determine the value of N we balance the highest-order nonlinear terms in Eq. (2.8), analogously as in the classical Kudryashov method. Supposing and are the highest-order nonlinear terms of Eq. (2.8) and balancing the highest-order nonlinear terms we have
Step 4. Substituting Eq. (2.9) into Eq. (2.8) and equating the coefficients of to zero, we get a system of algebraic equations. By solving this system, we obtain the exact solutions of Eq. (2.8). The obtained solutions can depend on the symmetrical hyperbolic Fibonacci functions proposed by Stakhov and Rozin [40]. The symmetrical Fibonacci sine, cosine, tangent, and cotangent functions are, respectively, defined as
3 Applications
3.1 Space-time fractional modified Benjamin-Bona-Mahony (mBBM) equation
We first apply the method to the space-time fractional mBBM equation in the form
where , , u is the function of and v is a nonzero positive constant.
This equation was first derived to describe an approximation for surface long waves in nonlinear dispersive media. It can also characterize the hydromagnetic waves in a cold plasma, acoustic waves in harmonic crystals, and acoustic gravity waves in compressible fluids.
We proceed by considering the traveling wave transformation,
where k, c, are constants.
Equation (3.1) can be reduced to the following ordinary differential equation:
Also we take
where . We note that the function Q is the solution of . Balancing and in Eq. (3.3), we compute
Thus, we have
and substituting derivatives of with respect to ξ in Eq. (3.4) we obtain
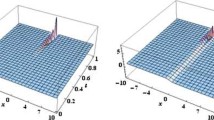
Substituting Eq. (3.7) and Eq. (3.8) into Eq. (3.3) and collecting the coefficients of each power of , setting each of the coefficients to zero, solving the resulting system of algebraic equations we obtain the following solutions (see Figures 1-8).
Case 1:
Inserting Eq. (3.9) into Eq. (3.6), we obtain the following solutions of Eq. (3.1):
Case 2:
Inserting Eq. (3.9) into Eq. (3.6), we obtain the following solutions of Eq. (3.1):
3.2 The space-time fractional potential Kadomstev-Petviashvili (PKP) equation
We next consider the following the space-time fractional potential Kadomstev-Petviashvili (PKP) equation:
where , .
We proceed by considering the traveling wave transformation,
where k, l, c, are constants.
Equation (3.15) can be reduced to the following ordinary differential equation:
Also we take
where .
We note that the function Q is the solution of . Balancing the linear term of the highest order with the highest-order nonlinear term in Eq. (3.17), we compute
Thus, we have
and substituting derivatives of with respect to ξ in Eq. (3.18) we obtain
Substituting Eq. (3.21), Eq. (3.22), and Eq. (3.23) into Eq. (3.17) and collecting the coefficient of each power of , setting each of the coefficients to zero, solving the resulting system of algebraic equations we obtain the following solutions (see Figures 9-16):
Inserting Eq. (3.24) into Eq. (3.20), we obtain the following solution of Eq. (3.15):
4 Conclusion
We have extended the modified Kudryashov method to solve fractional partial differential equations. As applications, for the space-time fractional potential Kadomstev-Petviashvili equation we found similar solutions to the ones previously obtained in [26, 32]. However, for the space-time fractional modified Benjamin-Bona-Mahony equation we have obtained new symmetrical hyperbolic Fibonacci function solutions with differences from the solutions obtained before [25]. If we take , we can also find the other hyperbolic solutions similar to [25, 26, 32]. The method is based on the homogeneous balancing principle. Therefore, it can also be applied to other fractional partial differential equations where the homogeneous balancing principle is satisfied. We can easily conclude that symmetrical hyperbolic Fibonacci function solutions for the space-time fractional modified Benjamin-Bona-Mahony equation have not been reported in the previous studies.
References
Zhang S: Application of Exp-function method to a KdV equation with variable coefficients. Phys. Lett. A 2007, 365: 448–453. 10.1016/j.physleta.2007.02.004
Misirli E, Gurefe Y: Exp-function method to solve the generalized Burgers-Fisher equation. Nonlinear Sci. Lett. A 2010, 1: 323–328.
Misirli E, Gurefe Y: Exp-function method for solving nonlinear evolution equations. Math. Comput. Appl. 2011, 16: 258–266.
Liu S, Fu Z, Liu S, Zhao Q: Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289: 69–74. 10.1016/S0375-9601(01)00580-1
Yan Z:Abundant families of Jacobi elliptic function solutions of the -dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18: 299–309. 10.1016/S0960-0779(02)00653-7
Tascan F, Bekir A, Koparan M: Travelling wave solutions of nonlinear evolution equations by using the first integral method. Commun. Nonlinear Sci. Numer. Simul. 2009, 10: 1810–1815.
Abbasbandy S, Shirzadi A: The first integral method for modified Benjamin-Bona-Mahony equation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15: 1759–1765. 10.1016/j.cnsns.2009.08.003
Zayed EME, Gepreel KA:The -expansion method for finding traveling wave solutions of nonlinear partial differential equations in mathematical physics. J. Math. Phys. 2009., 50: Article ID 013502 10.1063/1.3033750
Wanga M, Lia X, Zhanga J:The -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372: 417–423. 10.1016/j.physleta.2007.07.051
Soliman AA, Abdo HA: New exact solutions of nonlinear variants of the RLW, the PHI-four and Boussinesq equations based on modified extended direct algebraic method. Int. J. Nonlinear Sci. 2009, 7(3):274–282.
Salas AH, Gomez CA: Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation. Math. Probl. Eng. 2010., 2010: Article ID 194329 10.1155/2010/194329
Podlubny I Math. Sci. Eng. In Fractional Differential Equations. Academic Press, New York; 1999.
Bhrawy AH, Baleanu D: A spectral Legendre-Gauss-Labatto collacation method for a space-time fractional advection diffusion equations with variable coefficients. Rep. Math. Phys. 2013, 72: 219–233. 10.1016/S0034-4877(14)60015-X
Jafari H, Nazari M, Baleanu D, Khalique CM: A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66: 838–843. 10.1016/j.camwa.2012.11.014
Mehdinejadiani B, Naseri AA, Jafari H, Ghanbarzadeh A, Baleanu D: A mathematical model for simulation of a water table profile between two parallel subsurface drains using fractional derivatives. Comput. Math. Appl. 2013, 66: 785–794. 10.1016/j.camwa.2013.01.002
Momani S, Odibat Z, Erturk VS: Generalized differential transform method for solving a space- and time-fractional diffusion-wave equation. Phys. Lett. A 2007, 370: 379–387. 10.1016/j.physleta.2007.05.083
El-Sayed AMA, Behiry SH, Raslan WE: Adomian’s decomposition method for solving an intermediate fractional advection-dispersion equation. Int. J. Nonlinear Sci. 2010, 59: 1759–1765.
Hu Y, Luo Y, Lu Z: Analytical solution of the linear fractional differential equation by Adomian decomposition method. J. Comput. Appl. Math. 2008, 215: 220–229. 10.1016/j.cam.2007.04.005
Saadatmandi A, Dehghan M: A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 2010, 59: 1326–1336. 10.1016/j.camwa.2009.07.006
Inc M: The approximate and exact solutions of the space- and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345: 476–484. 10.1016/j.jmaa.2008.04.007
Wua G, Lee EWM: Fractional variational iteration method and its application. Phys. Lett. A 2010, 374: 2506–2509. 10.1016/j.physleta.2010.04.034
Elbeleze AA, Kilicman A, Taib BM: Fractional variational iteration method and its application to fractional partial differential equation. Math. Probl. Eng. 2013., 2013: Article ID 543848 10.1155/2013/543848
Zhang S, Zhang HQ: Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375: 1069–1073. 10.1016/j.physleta.2011.01.029
Meng F, Feng Q: A new fractional sub-equation method and its applications for space-time fractional partial differential equations. J. Appl. Math. 2013., 2013: Article ID 481729 10.1155/2013/481729
Alzaidy JF: Fractional sub-equation method and its applications to the space-time fractional differential equations in mathematical physics. Br. J. Math. Comput. Sci. 2013, 3: 153–163.
Alzaidy JF: The fractional sub-equation method and exact analytical solutions for some nonlinear fractional PDEs. Am. J. Math. Anal. 2013, 11: 14–19.
Guo S, Mei L, Li Y, Sun Y: The improved fractional sub-equation method and its applications to the space-time fractional differential equations in fluid mechanics. Phys. Lett. A 2012, 376: 407–411. 10.1016/j.physleta.2011.10.056
Zheng B: Exp-function method for solving fractional partial differential equations. Sci. World J. 2013., 2013: Article ID 465723 10.1155/2013/465723
Lu B: The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 2012, 395: 684–693. 10.1016/j.jmaa.2012.05.066
Younis M: The first integral method for time-space fractional differential equations. J. Adv. Phys. 2013, 2: 220–223. 10.1166/jap.2013.1074
Meng F: A new approach for solving fractional partial differential equations. J. Appl. Math. 2013., 2013: Article ID 256823 10.1155/2013/256823
Zayed EME, Amer YA, Shohib RMA:Exact traveling wave solutions for nonlinear fractional partial differential equations using the improved -expansion method. Int. J. Eng. Appl. Sci. 2014, 7: 18–31.
Jumarie G: Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput. Math. Appl. 2006, 51: 1367–1376. 10.1016/j.camwa.2006.02.001
Jumarie G: Fractional partial differential equations and modified Riemann-Liouville derivative new methods for solution. J. Appl. Math. Comput. 2007, 24: 31–48. 10.1007/BF02832299
Kudryashov NA: One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 2248–2253. 10.1016/j.cnsns.2011.10.016
Ege SM, Misirli E: The modified Kudryashov method for solving some evolution equations. AIP Conf. Proc. 2012, 1470: 244–246.
Ege SM, Misirli E: Solutions of the space-time fractional foam-drainage equation and the fractional Klein-Gordon equation by use of modified Kudryashov method. Int. J. Res. Advent Technol. 2014, 2(3):384–388.
Kabir MM: Modified Kudryashov method for generalized forms of the nonlinear heat conduction equation. Int. J. Phys. Sci. 2011, 6: 6061–6064.
Kabir MM, Khajeh A, Aghdam EA, Koma AY: Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Methods Appl. Sci. 2011, 34: 244–246.
Stakhov A, Rozin B: On a new class of hyperbolic functions. Chaos Solitons Fractals 2005, 23: 379–389. 10.1016/j.chaos.2004.04.022
Acknowledgements
This research is supported by Ege University, Scientific Research Project (BAP), Project Number: 2012FEN037.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ege, S.M., Misirli, E. The modified Kudryashov method for solving some fractional-order nonlinear equations. Adv Differ Equ 2014, 135 (2014). https://doi.org/10.1186/1687-1847-2014-135
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-135