Abstract
Background
Circadian clocks are biological oscillators that regulate molecular, physiological, and behavioral rhythms in a wide variety of organisms. While behavioral rhythms are typically monitored over many cycles, a similar approach to molecular rhythms was not possible until recently; the advent of real-time analysis using transgenic reporters now permits the observations of molecular rhythms over many cycles as well. This development suggests that new details about the relationship between molecular and behavioral rhythms may be revealed. Even so, behavioral and molecular rhythmicity have been analyzed using different methods, making such comparisons difficult to achieve. To address this shortcoming, among others, we developed a set of integrated analytical tools to unify the analysis of biological rhythms across modalities.
Results
We demonstrate an adaptation of digital signal analysis that allows similar treatment of both behavioral and molecular data from our studies of Drosophila. For both types of data, we apply digital filters to extract and clarify details of interest; we employ methods of autocorrelation and spectral analysis to assess rhythmicity and estimate the period; we evaluate phase shifts using crosscorrelation; and we use circular statistics to extract information about phase.
Conclusion
Using data generated by our investigation of rhythms in Drosophila we demonstrate how a unique aggregation of analytical tools may be used to analyze and compare behavioral and molecular rhythms. These methods are shown to be versatile and will also be adaptable to further experiments, owing in part to the non-proprietary nature of the code we have developed.
Similar content being viewed by others
Background
Eukaryotic organisms evolved clocks as an adaptation to geophysical cycles such as day and night or high and low tides or the passing seasons [1]. These clocks are oscillators that control timing in a broad range of processes such as rhythms in gene expression [2], and navigational mechanisms for migratory flight [3]. Studies on the nature of such clocks – whether at the level of gene expression or behavior – most often rely on the measurement of rhythmic processes by repeated sampling over time. Thus, the analysis of circadian clock function becomes the analysis of time series.
The fruitfly, Drosophila melanogaster, has been the outstanding model organism for studying genetic, molecular, neural and behavioral substrates of circadian rhythms [reviewed, for example, in [4–6]]. Recent studies have demonstrated that many molecular components of a circadian clock, several of which were initially identified in Drosophila, exhibit clock function in mammals as well. Thus, the fruitfly has provided mechanistic hypotheses that can be used to evaluate other organisms [2, 7].
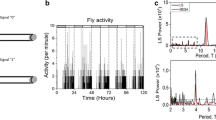
In any metazoan organism, the timing system is increasingly appreciated to be complex. For example, whereas rhythmicity of locomotor activity is governed by a pacemaker within a discrete set of neurons in the Drosophila brain [8, 9], molecular and physiological studies have also established the presence of autonomous circadian clocks in isolated appendages and excretory structures [10–12]. Moreover, the molecular mechanisms underlying clock function in these tissues may not be identical [13]. Finally, many rhythmic phenotypes expressed in flies can occur on different time scales. Figure 1 portrays 6 examples to illustrate the different levels of rhythmicity commonly studied in D. melanogaster. Each of these rhythms has heretofore been analyzed using a separate analytical technique. The periodic pattern of eclosion (emergence of the adult at the end of metamorphosis) and the pattern of adult locomotion (Figure 1a,b) are classic examples of circadian rhythms, which are typically analyzed by application of periodogram functions [14–17]. Figure 1c and 1d display examples of daily molecular rhythms for a whole fly and a pair of dissected wings, as reported in real time by luciferase-encoding DNA fused to regulatory sequences of the period (per) clock gene; these gene-product fluctuations have been analyzed using functions other than periodograms [10, 18]. Drosophila rhythms are also evident on other time scales besides circa-24 hours. Courtship song, for example, consists of a series of sinusoidal hums and trains of pulses that come from the male's wing vibrations. The intervals between these pulses (interpulse intervals, or IPIs) have been shown to vary rhythmically with a period near one minute in D. melanogaster[19, 20]. The trace shown in Figure 1e is taken from a digitized recording of the male courtship song, and such acoustical data have been subjected to still further kinds of time-series analysis [20–22]. Finally, at the highest frequency among these examples of periodic biological fluctuations, the heartbeat of the fruitfly exhibits a rhythm depicted in Figure 1f. It is driven by a pacemaker oscillator with a frequency on the order of about 2 Hz [23, 24]. Although heartbeat, courtship song, and locomotor-activity rhythms occur on different time scales, the mechanisms underlying these different rhythms could be related. For example, mutations of the per gene affect both circadian and courtship song rhythms [19, 20], but not heartbeat [25].
Rhythms of Drosophila melanogaster. The fruitfly generates behavioral, molecular, and physiological rhythms on several different time scales. Examples (a) through (d) depict circadian rhythms, while (e) and (f) involve ultradian (high-frequency) cycles. The eclosion rhythm, plotted in (a) as numbers of emerging flies over time, is a population rhythm associated with metamorphosis from the pupal to the adult stage. In constant darkness (DD) emergence of adults from the pupal stage typically occurs in the early part of the subjective day, corresponding to literal daytime in light-dark (LD) cycles (alternating white and shaded blocks, left side of plot). (b) Adult behavioral rhythms are usually assayed by monitoring daily locomotor activity. The behavioral record shown is that of an adult wild-type male. The temporal distribution of activity was measured by the number of times he tripped an optical switch with the counts typically collected every half hour for several days. The photic conditions are depicted as in (a). (c) Activity of a firefly luciferase transgene driven by the timeless promoter. A transgenic male ingested luciferin substrate; and a rhythmic signal of bioluminescense was registered each hour, leading in this case to plotting of bioluminescent counts over a six-day timespan. (d) An isolated wing pair, dissected from the same type of transgenic fly as in (c), also displayed rhythmicity when bathed in a luciferin-containing medium. In this example the data are normalized as described in the text. (e) A one-second bout of male courtship song, the beginning of which (between 0 and 0.2 seconds) consisted of "sine" singing (generation of humming sounds by male wing vibrations). The sine-song episode proceeded into a train of tone pulses, which are produced at a rate of ca. 30 per second (by D. melanogaster males) such that the interpulse interval (I PI) is ca. 35 msec. An IPI rhythm is defined by systematic increases then decreases, etc., in the rates of pulse production; the duration of one such cycle is ca. one minute (in songs of this species). The ordinate for this song-bout plot is in arbitrary units, because this record reflects changes in voltage that have more to do with the monitoring equipment than the changes in pressure corresponding to varying sound levels per se. (f) A pupal cardiogram. The rhythmic heartbeat moves blood (hemolymph) throughout the open circulatory system of the animal. The motion of the heart muscle is plotted in arbitary units because the relative changes in voltage reflect changes in illumination (with respect to a non-invasive optical recording technique) produced by the muscle as it moves.
Precise quantitative tools are needed for the analyses of such rhythms. In addition, a unified set of analytical methods would allow for comparisons to be made between rhythms of different types (e.g., behavioral vs. molecular) and time scales (e.g., circadian locomotor rhythm vs. the rhythmic IPI in courtship song). However, we have been unable to find such methods for the analysis of rhythms. This deficiency extends to the analysis of changes in the phase of rhythms induced (usually) by environmental stimuli. Although the resulting "phase response curves" are routinely plotted (showing the elementary magnitudes and directions of phase shifts), additional matters revolving round phase analysis are rarely addressed.
To make such comparisons possible we have substantially modified, extended, and integrated a set of computational tools, such that they may be applied to the analysis of any rhythmic process. We not only describe these tools, and apply them in several specific examples, but also present the reasoning and goals underlying our choice of tools.
We cover four general topics in time-series analysis. First, signal acquisition: sampling and inspection of the raw data. Second, signal conditioning: preparation of the data for further analysis by removal of high frequency noise, long-term trends and other extraneous and confusing perturbations in the data. Third, estimation of rhythmicity and period. Fourth, analysis of phase, including determination of phase response curves, phase coherence, and the comparison of phase among groups.
Results and Discussion
Signal acquisition
The tools described below are applications of signal analysis protocols. For our purposes, the signal is defined as the data recorded over time. For the locomotor activity and eclosion assays, these data correspond to the number of light beam interruptions per half hour over time. For the luciferase reporter assay data they correspond to the intensity of bioluminescence sampled hourly (see Materials and Methods for further details). In this section we consider the acquisition and description of the signals along with some pertinent analytical constraints.
In circadian studies sampling typically occurs at evenly spaced intervals of time, every hour or half hour. The sampling rate defines the shortest cycle that can be measured. For instance, if the sampling rate in a locomotor activity experiment is once per hour, then it would be possible to evaluate periodicities down to two hours, but no shorter, because a minimum of two points is required to describe a cycle. Put in frequency terms, this means the sampling rate must be twice that of the highest frequency to be analyzed; this limit is the so-called Nyquist frequency [26]. At the other end of the spectrum, it follows that the longest period that can be measured in a time series is determined by half of the length of that series. These high and low frequency are noteworthy because the presence of fluctuations at either end of this range can influence the analysis of circadian rhythmicity [see [21] for examples involving courtship song cycles].
Although we may be interested in circa-24 hour rhythms, it is often the case that other periodicities are represented within the signal. For example, ultradian rhythms, periodicities in the range of 5 to 18 h, may be present [for example, [27, 28]]. While the latter rhythms are inherently of interest [29, 30], they may nevertheless interfere with the analysis of the 24-hour components of the signal. Similarly, there may be long-range trends in the data; for instance, behavioral or enzymatic activity might slowly diminish over the duration of the experiment; thus, phenomena that could be the result of aging or chemical substrate depletion may produce temporally based changes that would be unrelated to clock function (see Figure 3; 10). These trends appear as very low frequency periodicities and can also interfere with the assessment of 24 hour periodicities. We will describe methods for filtering out both short and long period noise, aimed at emphasizing the periodicity of interest within the signal.
The length of the data set – hence the number of cycles present – affects the outcome of the analysis for period length. As discussed below, the confidence in the estimate of the period is directly related to the number of cycles in an experiment. Molecular studies on cycling gene products have commonly led to a single cycle's worth of data. It is not possible to estimate period rigorously or even to demonstrate the presence of true rhythmicity based on just 24 hours or 36 hours of sampling. With more cycles, say one or two weeks' worth of data, a more reasonable and precise assessment of period becomes possible. we wish to emphasize that sampling more frequently over a given duration of time has no effect on the accuracy of this estimate [31].
Although more sophisticated analyses such as autocorrelation and MESA (described below) are required to evaluate rhythmic signals quantitatively, it is often possible to make meaningful qualitative assessments by inspecting a plot of raw data. As an alternative to looking at records from a series of individual subjects, it is informative to evaluate the average signal for the group. To accomplish this, we combine data from individuals by calculating a mean level for each time point. This can clarify the phenotype, because any random variation present within various time segments of individual records is lost when such records are averaged.
By way of example, we recently studied luciferase (luc) reporter activity in dissected antennae in order to evaluate the effects of the cryptochrome-defective cryb mutation on a circadian clock that operates in the Drosophila antenna. The luc reporter was driven by a portion of the period (per) gene (its 5'-flanking sequences and those encoding the N-terminal 2/3 of the protein) in some cases or the 5'-flanking sequences of the timeless (tim) gene in the others; these molecular constructs were introduced into the D. melanogaster genome by germline transformation [32, 18, 33]. Reporter activity was sampled from an enzymatic reaction (luciferase oxidizing luciferin, present in the medium surrounding the antennae); the reaction produces a bioluminescent signal that is measured in counts per second once each hour [13]. One genetically based comparison made in this study involved the effects of the (normal) cry+ allele compared with that of cryb, tested in LD 12:12 (12 hours of light followed by 12 hours of darkness, over the course of about 5–6 cycles per specimen). Based on the analysis and tabulation of each individual specimen, 26% of the cryb samples (carrying either of the luc transgenes) showed rhythmicity in this assay as compared with 86% of the cry antennal pairs [13]. We inferred from this set of results that the mutation affects clock function in a manner separate from the photoreceptive role played by CRY protein [34].
In Figure 2 we plot and analyze the average luminescence of antennal pairs collected in LD12:12 to compare cry+ versus cryb. Tabulated data from individual specimens indicated that one quarter of the cryb samples were rhythmic (see Table 1 in [13]). However, plotting the average data for each genotype (Fig. 2) uncovers a more extreme difference between cry+ and cryb. Indeed, in contrast to the smooth sinusoidal appearance of the cry+ signal plotted in the leftmost panel of the top row, inspection of the averaged (but otherwise unconditioned) data plotted in the leftmost panel of the bottom row reveals little, if any, rhythmicity evident for the cryb tissues. Given that the effect of averaging is to smooth a time series and potentially emphasize rhythmicity, the absence of obvious periodicity in cryb, as shown qualitatively in the bottom left panel in Figure 2, suggests that the antennal cryb phenotype is typically arrhythmic in LD12:12. We will return to the other panels in Figure 2 when we discuss the quantitative analysis of periodicity using autocorrelation and MESA.
timeless-driven, luciferase-reported rhythmicity in cultured antennae. These appendages were taken from transgenic (but otherwise rhythm-normal) flies (cry+, n = 56) or those expressing a cryptochrome mutation (cryb, n = 80) and monitored for luminescence in LD as noted in Figure 1d. Top row, analysis of cry+ specimens; bottom, cryb. The column of panels on the left shows mean luminescence values (across specimens) plotted vs. time. Mean numbers of counts/hour/specimen-pair (for antennae of each genotype) are given in the upper right hand corners of this column. The gray shadings surrounding the plotted lines denote standard errors of the mean (SEM). The second column from the left shows detrended, normalized data. The fluctuating luminescence values re-plotted in this way reveal a genotype difference: the cry+ antennae were (on average) smoothly rhythmic (given the fairly clean, sinusoidal oscillations of tim-controlled luciferase activity), whereas the cryb group gave bumpier results. However the detrending treatment of both data sets reveals both groups of antennae to be periodic for this enzymatic reporting of clock-gene expression. The third column from the left shows the results of applying an autocorrelation function to the luminescence data, which evaluated the detrended, normalized data from each group. The shapes of and values associated with these correlograms indicate that each data set is rhythmic (confirming the impression from the second panel). The asterisk above the third peak (offset from 0, for which the data were perforce perfectly correlated with each other) indicates the point used to assess the Rhythms Index (Rl), a measure of rhythm strength (see text). The right-most column shows the results of maximum entropy spectral analyses (MESA), a method applied independently to estimate periodicity in these time series. The abscissa positions and heights of the peak in the MESA plots indicate the principal periodicities by which the cry+ and cryb antennae exhibited systematically fluctuating luciferase activity.
Trends affecting the analysis of adult locomotion. Behavior of a consistently behaving wild-type fly (top row) was compared to that of a wild-type adult that displayed decreasing activity toward the end of the behavioral record (bottom row). Locomotor activity was monitored in constant darkness, as indicated by shading throughout the actograms in the left-most column. Within each actogram, a given row shows two consecutive days of activity; the second such day is re-plotted in the left half of the next row down (thus, consecutive days of locomotion can be viewed both horizontally and vertically); heights of bars within a given actogram row reflect varying amounts of locomotion per half-hour data-collection bin. Note the white bar on day 15 in both actograms, which indicates that the data collection system crashed and rebooted. In the column second from the left, the locomotor data are re plotted as counts vs. time, This presentation reveals that the fly whose behavior is shown (and analyzed) in the bottom row became less active between days 9 12. The third column from the left shows the autocorrelation plot for these behavioral records, which indicate rhythmicity in the data; but the correlogram at the bottom is relatively irregular, with its wandering baseline compared to the one in the top row – a reflection of the "signal decline" in the corresponding locomotor record (bottom row). In the rightmost column, the MESA plots also reflect this behavioral difference, in that there is increased spectral density for relatively high abscissa values in the bottom plot compared with the spectral result in the top row. These features of the analytical results (in the right half of the figure) resonate with the long-term trend exhibited by the bottom-row fly vis a vis the top one.
Signal conditioning
When there are elements within a signal that interfere with the extraction of periodicities in the circadian range (or any range of interest), the raw data often need to be filtered for further study. Here, we discuss our choice and application of techniques for such preparation. Three problems will be addressed by application of a digital filter: 1) the presence of a shifting temporal baseline (i.e., trend), 2) the presence of high frequency noise, and 3) comparison between types of measurement (i.e., normalization).
There are two types of linear effects that can interfere with subsequent analyses. First, the signal could decrease or increase monotonically and at a constant rate producing a linear trend in the data. For example, as an animal ages, the amount of locomotor activity can decrease slowly. Alternatively, it might rise rapidly in a sort of "death dance"(as observed in Drosophila locomotor records) as the animal nears the end of its duty cycle. Figure 3 shows two examples of behavioral records from individual flies. The top row comes from a healthy, robust individual wild-type fruitfly; the bottom row is a record from another individual, whose activity dwindled. The leftmost plot is called an actogram (see caption for details); next to it is the raw data plot for each individual. We looked at 92 individual records from this experiment and found that 12 of these (13%) showed this sort of gradual decline or increase in the general level of activity over the course of the experiment. The behavioral trends associated with aging may have linear as well as non-linear components (see below).
In a second type of linear effect, the rhythmic component of a signal could be obscured by high baseline activity. This could occur, for instance, if the peak to trough variation were 30 arbitrary units, with the mean levels being in the thousands. In such a case, even though the rhythmicity might be quite strong in the circadian range (with very little variability from peak to peak), the rhythm could nevertheless be inaccessible to the method of analysis. This elevated baseline is also eliminated by removing the linear trend because the mean level is reduced to zero (see below).
Figure 4 illustrates the effects of removing this type of linear trend. The signal shown in Figure 4a is taken from a tim-luc;cry+ antennal specimen evaluated using the luciferase assay in constant darkness. The dashed line was fit by regression to the data using the method of least squares [35]. This line defines the linear trend in the data. Subtracting the value of each point on the trend line from the corresponding data point removes the linear trend as well as the constant baseline, producing the curve shown in Figure 4b. The dashed line in 4b is the resulting regression line with slope and mean of 0. As a safeguard against interference from linear trends and the possibility that rhythmicity is obscured by the baseline level of output, we always remove the linear trend from the data as a first step in our analysis.
Removal of linear trend from a luciferase timecourse. (a) Reporter-enzyme activity emanating from a pair of tim-luc;cry+ antennae maintained in DD. The dashed line is a least squares regression line that was fit to these data. (b) The linear trend defined by this line was removed by subtracting the value on the line from the corresponding data point. Removal of this trend line results in the dashed line (in b). The luminescence fluctuations around this mean (which are necessarily altered in appearance by the detrending) indicates the remaining presence of nonlinear trends. After removal of these non-linear trends circadian rhythmicity is apparent (see text and Figures 5 and 6).
Butterworth filtering to minimize various frequency components within luciferase fluctuations. (a) Raw luminescence data from tim-luc;cry+ antennae. (b) Result of applying a low pass filter to remove periodicities < 4 hours from the timecourse shown in (a), resulting in the smoother-appearing timecourse shown in (b). (c) Result of applying a high-pass filter to these data to remove periodicities > 72 hours, such that relatively high-frequency fluctuations remain. Note that the high pass removes the decreasing-slope trend (cf. Figure 4). (d) Result of applying a 72-hour low pass filter to highlight the overall temporal trend in these data, by virtue of removal in this case of nonlinear components (see text).
Timecourse normalization. (a) Trend curve for antennal luciferase fluctation, from Figure 5d, indicated as a dashed line superimposed on that for the data themselves (Figure 5a). (b) Normalized and detrended data. Normalization was accomplished by dividing each data point by the corresponding point on the trend curve. This leads to a mean timecourse value of 1 and preserves appearance of percentage changes for the values fluctuating about the trend line. One reflection of this treatment (as discussed in Results text) is that the (processed) luminescence oscillation in (b) appears more robust compared with (a).
Even after this manipulation there is still a U-shaped aspect to the data (Fig. 4). Although the mean is now zero, the individual points are not uniformly distributed above and below the trend line along its entire length. This indicates a residual nonlinear trend. Such nonlinear trends are common in luciferase assays and are likely to be caused by the depletion of substrate from the medium over time [18, 10]. We use digital filters to remove non-linear trends from signals and also to smooth them when they contain high frequency noise (see below).
Digital filters are like optical filters, which pass one group of wavelengths while absorbing others. Thus, as white light can be filtered to yield any component spectral color, by analogy, specific periodicities within a signal can be easily eliminated using a filter algorithm [31]. Although it is not our intention to present a formal or rigorous review of digital filters (see [36], for example), we will introduce a simple filter and then discuss the slightly more sophisticated Butterworth filter which we use in our studies.
Chatfield [37] defines a filter as a function that takes a time series x(t) and transforms it into another time series y(t). The simplest and oldest example of such a filter is the moving average. For example, in an average that considers 5 consecutive points, 5 consecutive values from the original series x(t) are each multiplied by 1, the results are added, then divided by 5 to produce the corresponding y(t). The process moves ahead one time point and is repeated. Thus for every x(t) there is a y(t) consisting of an average of 5 members of the original set. This process will produce a smoothed series that preferentially reduces the amplitude of high frequency spikes in the data while preserving that of the larger periods which are of interest [36]. In this example, the coefficients have equal "weight". In more sophisticated filters, the coefficients normally have non-integer values to "tune" the output of the filter to pass different frequencies.
The Butterworth filter is an example of a more refined analytical treatment [36]. It is a recursive filter that operates on the data twice, incorporating the output of the first operation into a second. Also, it is a "real-time" filter in that it uses only present and past values, never "future" ones (e.g. Xt+1), as is employed in the moving average method described above. The number of recursions is referred to as the number of "poles". Thus if the filter acts on the data three times, it is termed a three pole filter. The Butterworth filter produces a phase shift in the data; so we always run the filter twice, once forward and once in reverse to maintain the integrity of phase (times of peak occurrences, for example; see below).
Applying the Butterworth filter to the data shown in Figure 4 removes high- and low-frequency interference. Together with the elimination of the linear trend, the outcome demonstrates the presence of circadian rhythmicity in this signal (Figures 5 and 6). This approach is especially powerful in a situation where the biological or molecular readout (putatively revealing the rhythmic process) is not robust – for example, the output from tim-luc or per-luc reporters in isolated antennae [10, 13].
Figure 5a shows the raw data from Figure 4a replotted for better apprehension of the time series. Figure 5b demonstrates the results from the operation of a low-pass filter on these data; the lower frequencies – representing longer periods-pass through the filter unscathed, while the higher frequency spikes are removed. Figure 5c shows the application of a high-pass filter, which removed the periodicities greater than 72 hours. Note that in this case the linear trend has also been removed so that the mean value drops to 0. The shape of the curve is now horizontal rather than U-shaped, because both types of trends are now absent (compare to Figure 4b). Finally, Figure 5d shows the results of the action of a low-pass filter with a 72 hour cutoff, allowing only periods longer than 72 hours to pass. The result is a curve that defines the contour of the nonlinear long-range trend in the data.
Defining a long range trend (as illustrated in Figure 5d) is key to our method for detrending and normalizing a signal. Normalization of the signal allows us to compare different kinds of rhythms to each other, because the units of analysis are eliminated. For example, one might want to evaluate whether the period of a molecular rhythm is the same as a behavioral rhythm in DD or, alternatively, whether the timing of the peak of such rhythms is the same. The luciferase assay and the locomotor activity assay would facilitate this sort of experiment. But such comparisons are complicated because it is not clear what it means to compare locomotor activity counts against counts of bioluminescence. However, if these units of analysis are eliminated, then the temporal features of two signals can be compared.
We accomplish normalization as follows: after a low-pass Butterworth filter is set to define a trend curve (see Figure 5d), we then divide each data point by the corresponding value in the low pass trend curve. This division has three effects, as depicted in Figure 6b: First, the units of measurement are removed from the data and the data are normalized. Second, the mean is adjusted to 1. Third, the nonlinear trend in the data is eliminated. When the nonlinear trend is removed in this way, the ratio of a data value to the corresponding value of the trend line is emphasized. This both corrects for the damping evident in 5c (a result in this case of luciferin depletion in the medium) and reveals that the rhythm is actually just as robust later in the experiment, even though it appears to be damping prior to normalization. To illustrate this point another way, consider that a change from 4000 cps to 2000 cps appears more dramatic than a drop from 100 to 50 even though both represent a 2-fold change; the ratio, and hence relative amplitude, is the same in both cases. Again, detrending the data by division emphasizes the ratio rather than the absolute value. Thus, it becomes evident that the actual oscillation is not damping (Figure 6).
One further application of filtering has proven useful for determining phase values. The Butterworth filter can be used as a "bandpass" with both a high and a low cutoff. This allows the investigator to focus on a precisely defined range of periods. Figure 7a shows raw data from monitoring Drosophila eclosion. Fig 7b shows these adult-emergence counts after a bandpass filter has been applied; this setting of the filter removes all periods shorter than 4 hours and longer than 40 hours. Figure 7c indicates the result of removing periods less than 15 hours and greater than 30 hours, which results in distortion of the data. We show this outcome to illustrate that care is required when establishing the cutoff limits of the bandpass. In the most severe and worst case scenario, application of a sharply-defined band pass filter to pure noise would result in a spectrum with a pseudopeak at the center of the filter's band. Thus, we end this section with a cautionary note about filters: the choice requires familiarity with the raw data (one reason for the earlier emphasis on qualitative scrutiny of data plots prior to quantitative analysis); a specific criterion or goal; and a conservative sense about whether the important components of the signal might be distorted. We say conservative because of the possibility that an artifact might be introduced into the analysis by the choice of filter parameters as illustrated in Figure 7.
Bandpass filtering limitations. That such limits can be too narrow is exemplified by analysis of Drosophila's eclosion rhythmicity. Number of flies emerging are given on the ordinates, plotted vs. time. (a) Raw eclosion data from a wild-type culture monitored in DD. (b) Result of filtering the data in (a) with a bandpass set between 4–40 hours, such that only periodicities with values in this timespan survive application of the filter. (c) Result of filtering with bandpass set between 18–28 hours; such that, when the window of excluded frequencies is small enough, the data take on an artificial appearance. The clarity achieved with wider limits is replaced by a loss of potentially useful detail, or, worse, by distortion (see text).
Estimation of rhythmicity and period
The conditioning procedures described above (detrending and normalization) prepare a signal for analysis. In this section we demonstrate tools for evaluating (1) periodicity in the circadian range, (2) the strength of a rhythm (if there is one), (3) whether or not the rhythm is a fluke, (4) the period of the rhythm. We discuss alternative methods for evaluating the period of behavioral rhythms as well as rhythms in the luciferase assay, including a method used in earlier studies called FFT-NLLS [10, 18].
To evaluate whether the data are periodic, we use autocorrelation (correlogram) analysis [37]. Briefly, the conditioned signal is paired with itself element for element, ordered in time. A coefficient of correlation is calculated in the standard manner [35] for the two identical ordered data sets. The calculation is repeated as the two series are slipped or "lagged" out of register with one another, one point at a time. When the lag between the series is 0, the correspondence is perfect and the correlation coefficient is 1; but when the two sets start to be offset, the correlation coefficient begins to decrease. If the series is random with respect to time, correlation will rapidly fall to low levels and remain there. If, however, there is a regular rhythm in the signal, then the peaks and troughs in the amplitude of the signal will slip back into register when the lag approximates the periodicity, causing the correlation to increase again. Further peaks will appear each time there is an alignment (i.e., for periodic harmonics, 24 h, 48 h, etc.). Rhythmic variation in this autocorrelation function uncovers periodicity. Note that as the lag between the data series increases, the number of nonoverlapping points increases and the autocorrelation analysis involves a diminishing portion of the signal. In addition, the calculation is done by first calculating the covariance and then dividing by the variance, thus the output is normalized. See Figures 2 and 3 for examples of the correlogram as applied to the luciferase assay and locomotor behavior, respectively.
A reasonable question is whether or not the periodicity signified by the outcome of an autocorrelation treatment can occur by chance alone. While strong periodicities from random records are unlikely, the presence of weaker pseudoperiodicity in a noisy signal is more likely. Such effects have been observed in the analysis of courtship song as a consequence of the sampling rate; fluctuating values from one point to the next suggest periodicity in the range of the Nyquist frequency; for the song records in question and analysis of the pulse-rate fluctuations, 20-s periods, against a background of 10-s sampling intervals [21]. It is possible to assess quantitatively how likely a given peak in an autocorrelation can be the result of chance alone. A 95% confidence interval can be computed based on the number of observations in the series equal to 2/√N. By convention, N is taken to be a constant rather than varying as data are 'lost' by lagging (37). The correlogram panels within Figs. 2 and 3 exemplify results with significant rhythmicities by this criterion. In practice we seek to demonstrate significant rhythmicity; however, a rhythmic series may fail this formal test of significance and appear to be rhythmic nonetheless. There is precedence for a less quantitative assessment of rhythmicity using the autocorrelation function [37, 38]. Accordingly, the shape of the analytical plot may show rhythmicity even if statistical significance is not reached, i.e., the plot shows repetition of the peaks at a regular interval. For example, if the shape of the correlogram is sinusoidal with a period in the circadian range, then we would interpret this to mean that there is a circadian rhythm in the data, even if the correlogram fails to show that the rhythm is statistically significant (see below for more detail). This convention has been applied where the size of the data set may be small (at most 180 data points in luciferase studies, for instance) making the confidence limit unrealistically high [13]. Thus, given a regular rise and fall in the correlogram, we would consistently consider those data to be rhythmic [see [37, 38] for more detail, also see [10, 39]]. While this assessment of rhythmicity is subjective (in contrast to the objective cutoff imposed by the 95% confidence interval), we guard against investigator bias by evaluating each record "blind" to genotype or treatment. In this way, the presence of a rhythm is not dismissed simply because the output is weak or noisy and the record is short. Note that the correlogram also gives an estimate of the period (see below).
Even when the autocorrelation function portrays statistically significant rhythmicity, it is still possible that the data do not represent a truly rhythmic process. The signal could be an expression of chance, i.e., of random variation. To determine whether the phenomenon is indeed stochastic, we produce one or more random permutations of the original data in time. The power (variance) in the signal and the mean will be the same, but the original order of the time series will be completely lost. If the original periodicity is lost when the signal is randomized, this provides one more piece of evidence that the observed rhythm in the autocorrelation (and later spectrum) is real and believable. While this does not rigorously eliminate the possibility that the original series was pseudorhythmic by chance, it will show that the combination of analytical techniques used is not generating artifacts when given a randomized version of the original data. We term this process "shuffling" because we redistribute the data several times sequentially [see the following citations for examples [27, 39, 13]].
If the data demonstrate rhythmicity, it is important to specify numerically how "strong" the rhythmicity may be. This strength may be a function of the relative amplitude and regularity of the underlying physiological process or a reflection of the amount of noise in the signal, or the consequence of how many (putative) periods' worth of data were collected. Given that the autocorrelation function is a good measure of the amplitude across the entire span of the signal, and that the rate of "decay" in this function reliably assesses the long-range regularity in the data [37] we employ an index derived from this function as a measure of how rhythmic the data are. We assess the strength of the rhythm as the height of the third peak in the correlogram (counting the peak at lag 0 as the first peak), terming this number the Rhythmicity Index, or RI (see Figures 2 and 3). Statistical analysis employing the RI between different samples or groups is straightforward, because it is simply a correlation coefficient, which is normally distributed and dimensionless [35, 37]. This method was developed to measure and compare the strength of rhythms in Drosophila heart function [see [25], and especially 40, for a more rigorous presentation of the method), as well as for circadian luciferase expression in dissected antennae [13].
The choice of the third correlogram peak was not motivated by rigorous theoretical considerations but was also not arbitrary. Empirically, in analysis of heartbeat rhythms, the 3rd peak proved the most reliable. There are other practical considerations: in the case of circadian data, especially when only 4–5 days of data are available, the 3rd peak incorporates only half the original data (as the autocorrelation analysis is calculated each successive lag produces a loss of a data point for subsequent consideration, thus after one day 24 one hour points would be out of the analysis). Choosing peaks beyond the 4th one (and likely beyond the 3rd) could actually distort the outcome because the correlation would be based on such a small number of points [40].
Once the signal has been determined to contain a real rhythmic component, the next point to be addressed is what the period of the rhythm might be and how certain one can be of that estimate.
The heart of period estimation is Fourier analysis. Other methods have been used for biological time series with varying amounts of success. The most common non-Fourier-based technique currently in use in chronobiology is the " chi-squared periodogram" [41, 42]. Although serious objections have been raised in consideration of the periodogram (discussed from varying perspective by Whittaker and Robinson[42]; Kendall,[43]; Dowse and Ringo [39, 44] Enright [46], we continue to employ this method along with others discussed below.
Central to spectral analysis methods lies the discovery by Fourier that any function can be decomposed into a series of harmonic sine and cosine terms with coefficients determined by the goodness-of-fit to the data. Frequencies for which coefficients may be calculated are 1/N, 2/N, etc., where N is the number of data points, and range up to the Nyquist frequency dictated by the rate of sampling (see above). The vector sum of the coefficients for the sine and cosine terms at a given frequency represent the power in the signal attributable to that frequency [31]. Critically, this decomposition of the data is orthogonal, in the sense that the amplitude coefficients for each sinusoid frequency are independent of each other. The derivation of a given coefficient has no effect on any others [45]. A plot of the Fourier coefficients as a function of frequency or period yields a spectrum indicating any periodicity in the data and its frequency, the true periodogram (this use of periodogram is not the same as the Chi-squared periodogram traditionally used to evaluate circadian rhythms data [see [44]]). The area under the curve of the periodogram equals the variance in the data, which has now been partitioned according to the frequency and moved from the time to the frequency domain [37].
Figure 8a shows the linearly detrended plot from an isolated antennal pair expressing a tim-luc reporter sampled in hourly increments in the time domain (counts per second of bioluminescence over time). Figure 8b shows these same data plotted in the frequency domain. Note that, for convenience, circadian rhythm data plots are usually converted to period from frequency on the abcissa. Periods longer than 24 h normally result from long-term linear or nonlinear trends in the data (see above), just as shorter periods may be a result of either high frequency rhythms [27, 47] or high frequency noise.
Fourier filtering of luciferase-reported molecular rhythm. (a) Fluctuating antennal luminescence (from a tim-luc sped men pair), from which the linear trend was removed (cf. Figure 4); these data are plotted in the time domain. (b) Result of transforming the data in (a), such that they are now plotted in the frequency domain (abscissa: period, i.e., 1/frequency, for convenience). In (b) the most appreciable feature of the frequency domain occurs within the shaded region, wherein periods between 48 and out to 136 are represented. (c) Dismissal of Fourier coefficients corresponding to periods > 48 hours, to emphasize periodicity in the circadian range. (d) Transformation of the values represented in (c) back to the time domain, with such reconstructed data appearing to have lost the nonlinear trend.
In practice, Fourier analysis is no longer done by direct transformation of the raw data, but rather by variations of two basic methods. In the first general class of techniques, one takes the transform of either the autocovariance function or, more usually, the autocorrelation function [47]. As the latter effects a normalization of the data, the units of the spectrum are termed spectral density. When computing the autocorrelation function, data are lost at either end with each advancing lag, so computation values seldom proceeds past the point when about 1/3 of the original data set has been lost. To compensate for this loss, zeros are added to extend the series out to N lags [48, 49].
Alternatively, the data may be transformed directly, but with a computational shortcut called the Fast Fourier Transform, or FFT[47]. For this method the number of data points must be a power of two (2N; [37]). Obtaining exactly 2N data points is not always possible for experimental reasons so the convention has been to extend the data set by adding zeros out to the next higher integer power of 2. Zeros are also often added beyond this point to increase resolution (see discussion on resolution below [37]).
There are two problems associated with adding the zeros to pad out either the autocorrelation function or the raw data themselves. First, the abrupt end of the original data set followed by a string of zeros creates a sharp discontinuity and this artifact can cause problems in the resultant spectrum in the form of "side lobes" [47, 48]. One strategy for addressing this problem is to apply so-called smoothing or weighting functions to make the drop to zero less precipitous and reduce the appearance in the spectrum of the resultant artifactual bands called side-lobes [47, 48, 37]. But techniques for side-lobe suppression are in themselves problematic. There is no reason to presume that the next several data points would be zero and, in addition, perfectly good and real data near the end of the original series are corrupted when they are altered by the smoothing function [47, 48, 37]. We prefer to avoid using the FFT for these reasons. The technique described below avoids both problems offering excellent side-lobe suppression with no loss in resolution [50].
A major advance in spectral analysis was the development of Maximum Entropy Spectral Analysis, or MESA by Burg [48–51]. The reader is referred to [39] for a full treatment of the topic. MESA operates by first fitting an autoregressive model to the data. This model presumes that a datum at a given time point is a combination of a variable number of previous values and some stochastic process. Thus Xt = a1Xt-1 + a2Xt-2 + ... + an+Xt-n + Zt, where {a}'s are coefficients estimated from the data, n is the number of terms in the model, and Z is a stochastic process. A simple arithmetic operation turns the set of coefficients into what is termed the prediction error filter. Fourier methods are used to construct a spectrum, and we choose the number of estimates of period to assay in the data. Typically, for circadian analysis, we examine the data sets for periodicity at increments of 0.1 hours in the circadian range, but this resolution can be increased or decreased arbitrarily as warranted. Moreover, MESA is readily applicable to time series involving putative cycle durations well shorter or longer than one day.
The luciferase assay has been employed to address molecular rhythms in plants [52] and cyanobacteria [53] and mammals [54, 55] as well as in Drosophila. Typically, 5–7 cycles are evident in these studies. As explained below, the number of cycles in a signal indicates the theoretical resolution of the estimate for the period, i.e., whether an estimate of say 24.5 hours can be distinguished from an estimate of 24.0 hours depends on the number of cycles. We employ MESA to estimate the period of a rhythm in the luciferase assay, while using the correlogram to evaluate rhythmicity.
Drosophila locomotor activity rhythms are typically measured from 5 days to 2 weeks and in mice such measurements are often presented for a month or longer [56]. The behavioral rhythm has the form of a square wave with intervals of activity followed by intervals of inactivity (in contrast to the sinusoidal waveform of the luciferase rhythm). Moreover, the distribution of activity during the active part of the circadian cycle varies (not the temporal distribution of the interval of activity so much as the amount of activity at a given time within that interval from day to day). This variation can give rise to pseudorhythms that could skew the estimate of period using any of these statistical methods.
Our concern about such errors motivated a comparison between three different numerical methods for estimating circadian period. As shown in Table 1 we applied Autocorrelation, MESA and the "Chi-squared Periodogram" [57] to locomotor activity data generated by individuals who were either wild-type, cyc01/+, cyc02/+, or who had only one copy of the cyc locus (cyc-deletion/+) [58]. We advocate using these methods simultaneously to maximize accuracy (for example, if Autocorrelation analysis indicates that a signal is arrhythmic we reject any value from MESA because MESA does not evaluate rhythmicity and will return an estimate for any signal). We examined the estimates returned by each method separately to compute the averages shown in Table 1. Moreover, although direct inspection of the data lacks the objectivity of a computer program, a straightforward view of the actogram provides a check against accepting numerical output that might be obviously skewed as described above.
In fact, for these experiments, the analytic methods are in agreement (see Table 1). The consistency of results across genotypes in these analyses further validates this multi-pronged approach: The wild-type flies and those carrying cyc-gene variants (mutations or a deletion of the locus) gave the same overall rhythmicity as well as period values. These results differ with previous results (based on periodogram alone), which indicated that cyc01/+ and cyc-deletion/+ heterozygotes exhibit longer circadian periods compared with wild-type [58]. Table 1 also demonstrates that these methods fail to correlate in a rank order test even though they yield the same estimates on average (see Table 1 for details).
We have observed that MESA may show a greater spectral density around 12 hours than at 24 hours. This is often the case when estimating the period of a rhythm in LD 12:12, for example. Such results say that a 12 hour period captures the rhythmicity in the data more completely than periodicity at a value representing a longer period. This outcome is a logical consequence of the bimodal locomotor activity profile under a light-dark cycle. In such cases, when a peak near 12 hours is greater than a mini-peak located near, say, 18 hours (or 24 or 27), our estimate of the rhythm becomes twice the period value of the major peak in the spectrum.
In summary, the considerations for estimating period of locomotor activity rhythms are similar to those we apply when estimating luciferase activity rhythms as described above. We use a subjective but systematic approach that can be summarized as follows: The signal is evaluated by an investigator who is blind to genotype or treatment. Rhythmicity is assessed by the autocorrelation function. While the autocorrelation function may provide statistical confidence, we typically accept the shape of the correlogram as the criterion for rhythmicity. If the correlogram is sinusoidal with peaks and troughs occurring in the circadian range, we accept the signal as rhythmic – even when the autocorrelation function fails to be statistically significant. This subjective criterion follows from the fact that the confidence interval of the correlogram is not based on variability in the signal but solely on the number of data points taken in the experiment (see [37]). Following inspection of the signal and the correlogram, several methods are used to estimate period. We tend to use MESA and the correlogram for luc data and we also include the correlogram and chi-squared periodogram analysis for locomotor activity or eclosion. This permits a reality check on the nature and quality of the putative rhythmicity, including the provision of 3 independent estimates of the period. It is especially important to analyze such results in a versatile manner when the locomotor data were collected for a relatively small number of days (Table 1).
The Fourier transform can also be employed as a filter. The data are first transformed directly and the coefficients plotted. If there is an area of the spectrum that is interfering with the analysis, it may be removed cleanly by zeroing out the coefficients in those areas of the spectrum. The original data set is then reconstituted by use of the inverse Fourier transform, which simply runs the system in reverse. The resulting time series, "Fourier-filtered" in this manner, is the original minus the spectral elements that were causing the problem. Recall that the sine and cosine terms in the original Fourier decomposition were orthogonal; thus the only areas of the spectrum affected are the ones whose coefficients were removed.
Figure 8c shows the changes in the spectrum portrayed in 8b after all periods longer than 40 hours were removed by zeroing coefficients beyond that value. The filtered signal (Fig. 8d) gives a view of the data without influence by long period trends in the data set. Note the similarity between the result of the Fourier filter shown in Figure 8d and the result of the Butterworth Filter shown in Figure 5c. As treatment with the Butterworth filter produces comparable results and also normalizes the data, we regularly use this technique, reserving the Fourier filter for unusual situations. For example, when an ultradian rhythm is embedded in a strong circadian rhythm, Fourier filtering is the most effective method for looking solely at the ultradian rhythm (HB Dowse, unpublished observations). This is exemplified by the isolation through Fourier filtering of a circhoral (approximately hourly) rhythm in human core body temperature found against a background of a strong circadian temperature rhythm [59].
One further method of period estimation needs to be mentioned, as we and others have used it in the past [10, 18]. It is called Fast Fourier Transform – Non Linear Least Squares analysis (FFT-NLLS). This method estimates the period of a rhythm with the Fast Fourier Transform, then uses that value as a starting point to fit a sinusoid to the data by non linear least squares estimation [10, 18]. This would presumably find a period "in between the cracks" of the original FFT. There are problems with this approach which argue against its applicability. For the reasons given above, viz. relatively low resolution compared with MESA, along with the generation of artifactual side-lobes, we wish to avoid using the FFT and prefer to use MESA for estimates of the period. Finally, the pitfall of FFT-NLLS is that the curve-fitting operation associated with a probing sinusoid is sensitive to the presence of other periodicities in the data, variations in wave form from cycle to cycle, and random noise. We prefer to analyze the signal itself, rather than an idealized approximation of the data obtained from a curve-fitting algorithm.
We have referred to the limits of resolution in time series analysis. These issues are the same as those connected with resolution involved in optical interferometry and obey the same laws [60]. For example, the wider the spacing of the mirrors in the interferometer, the better the resolution [60]. Resolution in digital signal analysis is the capacity of a given system to separate two arbitrarily close frequencies into distinct peaks in the spectrum. As with optical systems, the longer the record, the closer the two peaks can be in frequency and still be separated. The fundamental reason for this can best be visualized by considering what happens to information when data are passed back and forth from the time domain to the frequency domain. If, for example, one is dealing with a lengthy locomotor record that contains bouts of rhythmic activity interspersed with inactivity, spectral analysis can indicate the presence of the rhythm but nothing about the local time-dependent features of the rhythm, such as when the periods of inactivity occur, amplitude changes over the course of the experiment, and transient phase shifts. The relatively large number of complete cycles in the data, however, yield very reliable information about the periodicity; and if there is more than one rhythm, the two periods can more likely be resolved by Fourier-based spectral analysis in the same manner that two wavelengths of light can be resolved into separate lines in a spectroscope [60]. The relationship between the number of cycles present in the data record and resolution is mathematically equivalent to the gain in spectral resolution with the increase in distance between mirrors in an interferometer [60]. On the other side of the coin, if a very short series is transformed, information about local conditions in the time domain becomes more precise at the expense of resolution in the frequency domain [the information in the time domain is more precise; but the resolution in the frequency domain is greatly reduced [38].
The relationship between the number of cycles and the resolution of period by Fourier analysis is known for an ideal spectrum [61]. Although the theory is beyond the scope of this paper, the resolution of two distinct periods based on 5 days of data is to within 0.3 hours and the resolution for one week is 0.2 hours. But these estimates are unrealistic in practice, because in the ideal situation period and phase are precise and time-invariant. By contrast, when actual experimental data are evaluated, the error for the estimate of the period will vary as a result of noise in the signal, peak-to-peak variation in the wave form, and variability in the period itself over the duration of the experiment. The standard deviation of the frequency estimate can be calculated [61]. In practice, for example, when comparing period estimates as a function of genotype, the means for each group are compared statistically rather than periods from two individuals. If a difference in the mean period in the two groups appears statistically significant, then we consider it believable even if the difference is small and approaches the theoretical limit of resolution for the length of the records.
Phase, phase response curves, phase coherence, and comparison of phase
If a process is rhythmic, it can be represented by a circle, with the phase of the rhythm represented by the angle of a vector. If two processes of identical period are occurring simultaneously, they may be compared with respect to their relative phase. Two questions regarding phase are typically addressed. The first asks how the clock can be reset and is addressed by examining the response of a rhythm to some incoming signal such as a pulse of light. Typically, this sort of question leads to the measurement of a phase response curve (PRC). The PRC plots changes of phase as a function of when a stimulus pulse (e.g., 5 minutes or 1 hour of light) is administered. Several methods for evaluating PRCs have been validated [62]; the method we use is Aschoffs Type II procedure. We will describe two methods for analyzing data used for evaluation of the PRC. The second question asks what is the phase of the rhythm within each cycle (or within a cycle on average)? This matter is addressed by estimating a given phase reference point (such as the peak) in a cycle. For instance one might want to evaluate whether a group of rhythmic subjects is coherent (phase-synchronized). Alternatively, one might want to know whether two or more groups of subjects exhibit maxima (and minima) for their fluctuating parameters at different times.
The most straightforward method for determining phase is to pick an easily identified landmark in the signal, usually a peak, and note its time either with respect to the actual time of day, or to that of the organism's subjective circadian day. The initial stage of applying this method usually requires a vigorous conditioning of the data to make them smooth enough, so that a peak, trough, or other landmark can be found reliably. Signal averaging and smoothing are typically necessary. Figure 9a and 9b show averaged raw locomotor activity data for flies that received a 5-minute pulse of light (Figure 9a) or control flies that were not perturbed by exogenous stimuli (Figure 9b). Figure 9c shows the smoothed curves obtained from these two groups superimposed on one another. Figure 9d plots the difference between these two groups on a daily basis, from which the estimate of the shift can be evaluated (see Figure caption for more details). Note that if the behavior of the group receiving the light pulse is affected, there may be transients. Transients result when the phase shift takes some number of cycles to be complete before the new steady phase is established. If transients are present they can be detected by this method.
Estimation of rhythm peaks for phase response curves. (a) Averaged locomotor activity (mean ± SEM, the latter indicated by dots), plotted for 6 males that had been individually monitored for locomotion. The photic conditions, indicated by the shading as in Figure 1, involved ca. 6 days of 12-h:12-h LD cycles followed by about the same number of DD ones. A 10-minute light pulse, timed according to the asterisk placed within a thin white stripe, was administered 4 hours after the final lights-off, i.e., early in the subjective nighttime. (b) Another set of 6 males maintained in the same conditions, except that they received no light pulse after proceeding into DD. (c) The data sets from (a) and (b), re-plotted together after smoothing them by application of a low-pass filter set with a cutoff of 12 hours. This treatment facilitates identification of peaks in both data sets, as indicated by the asterisks for the pulsed group and the crosses for the no-pulse group. (d) Difference between the two groups, plotted as changes in hours vs. time for each peak over the course of the LD -> DD monitorings. The timing of a given peak for the no-pulse group was subtracted from that for the light-pulsed group, resulting in depiction of a net phase delay for the latter flies in DD. The 3 rightmost points on the abscissa indicate stabilization of 3.5-hour, light-induced phase delay.
One disadvantage of the method depicted in Figure 9 is that it is subjective, i.e., whether a steady-state phase shift has occurred is a matter of judgement. A second method removes all subjectivity from the process and gives an estimate based on the data set in its entirety rather than on a day by day evaluation of the difference between two peaks. This method is based on cross-correlation analysis [37]. Cross correlation is much like autocorrelation but is used to compare two different signals instead of one data set against itself. A probing series, – exemplified here by the non-light-pulsed group of behaving flies (see Figure 10)-is lagged against the time series of interest – the light-pulsed group. If there is no difference in the phase between the two groups, there will be the usual peak of correlation at lag zero. If there is a phase difference, then that will be reflected quantitatively in a displacement forward or backward in the position of the central peak of the function. This is demonstrated in Figure 10, employing the same data treated in Figure 9. The advantage of this process is threefold: (1) it treats every data point, not just the time of the peaks; (2) it does not require excessive data conditioning before application of the principal piece of analysis; (3) it obviates the need for judgment calls by the analyst (such as when has the steady state been reached). Note that in Figure 10 we crosscorrelated the average of the two groups, but in principle an estimate of the variability in the data could be obtained by cross correlating each of the pulsed individuals against the control group.
Crosscorrelation to compute data points for phase-response curves. Using locomotor results from the two groups of flies in Figure 9, the data sets were cross-correlated starting from a time just after the light-pulse (Figure 9a) until the end of the locomotor records. Whereas autocorrelation evaluates the relationship between a data set with itself over time (see Figures 2, 3), crosscorrelation evaluates the relationship between two different data sets. The plot shows correlation coefficients plotted with respect to the lag (in hours) between the two (averaged) locomotor timecourses (see text). This comparison was used to determine whether there is a difference in phase between the untreated vs. light-pulsed flies. The lag is read as the phase-offset from 0 on the abscissa. This particular crosscorrelation analyses resulted in a "first" peak at -3.5, indicating a phase delay of that number of hours. This result agrees with that obtained in Figure 9, albeit less formally (i.e., by inspection of the plots in 9c and 9d).
The period of a rhythm does not predict its phase. For example, one might wish to determine the phase of a luciferase-reported molecular rhythm, with respect to the peak of tim-luc expression in a group of cultured tissue specimens maintained in LD12:12. As shown in Figure 11, the approach to this problem involves plotting the peak (the mean peak time within an experiment) for each individual specimen (isolated fly wings in this case) that has been examined on a unit circle using polar coordinates. A group mean vector is then determined. The direction of the vector indicates the phase of the group (by convention phase 0 corresponds to lights on), and the magnitude of this vector indicates the coherence of the group. Thus, in the extreme, if all the points were uniformly dispersed around the circle, the magnitude of the vector would be zero; whereas if they all occurred precisely in the same location, the magnitude of the vector would be 1. A statistic, Rayleigh's test, provides a z-score that makes it possible to assess whether the magnitude of the average vector is significant for the group, i.e., whether the individual phase values are clustered tightly enough to provide a significant estimate of the mean peak time [63].
Peak phase determination for a tim-luc timecourse. The fluctuating luminescence data were collected from a series of isolated, cultured fly wings in 12-h:12-h LD cycles. (a) The enzyme-reported molecular timecourse for each of 15 specimens. The appearance of synchronous waves suggests that the several heads exhibited similarly phased clock-gene-expression rhythmicities. (b) Scatter plot of mean peak phase values (per day) for each specimen. The zero-hour phase corresponds to the times of lights on, so 12 of the 15 specimens gave average peak luminescence in a 2 hour window preceding lights-on. (c) Unit-circle representation of the head-rhythm phase data. The circle defines a polar coordinate plot with radians transformed to hours. The inner dotted circle is the unit one and the dotted lines cross at the origin. The magnitude of a mean vector in this plot describes the coherence of the various phases of the head samples. The phase points taken from each specimen are plotted around the circle just beyond the unit circumference. The mean vector extends from the origin in the direction of -0.3 hours and has a magnitude that nearly reaches 1, indicating strong phase coherence.. The coefficient is a z-score and was determined to be signifiant at p < 0.01 by Rayleigh's test (see text).
In addition, one might ask whether two sample populations have the same phase. In Figure 12, we compare tim-luc activity in cultured wings vs. heads to ask whether the luciferase reporter activity peaked at the same time in these two tissues. In this case two average vectors are compared, and an F-statistic (Watson-Williams-Stevens test in [63]) is calculated to test whether the means are drawn from the same population or not.
Comparison of peak phases for wings vs. heads. tim-luc transgenic specimens were monitored for luminescence fluctuations in 12-h:12:-LD cycles. Labeling conventions are as in Figure 11c. Here, a 3.4-hour difference between the peak times for the wing (*) vs. head timecourses is indicated by the vector for the former data pointing to -0.3 and that for the head pointing to 3.1. This difference was found to be significant (F statistic, p < 0.01) by the Watson-Williams-Stevens test (see text).
More generally, the comparison of different rhythms will be required to analyze the relationships amongst molecular, physiological and behavioral rhythms. One feature of this analysis must be to examine how the phase of these various rhythms predict one another. For example, at a molecular level it seems that transcriptional component of a mammalian circadian clock involves the antiphase expression of transcriptional regulators [2]. to illustrate such comparisons across levels of analysis, we compare smoothed, normalized data from tim-luc expression amongst various isolated body parts, the entire fly, and locomotor activity in LD 12:12 (Fig. 13).
Comparison of behavioral phase for intact flies with that of luciferase-reported tim expression for whole animals and isolated body parts. (a) Rhythms of subject types given on the ordinate of the upper-left plot; all types except the top one involved luminescence rhythms. Mean signals are plotted for each (across flies or tissue specimens): behavior, n = 6; whole fly luciferase activity (live fly), n = 10; dissected antennae, n = 16; heads, n = 14; wings, n=15; bpdies (fly segnents posterior to the head), n = 15; legs, n = 24. In each case, the mean signal was smoothed with a 4-hour low-pass filter and normalized. In addition, the behavioral plot was been adjusted by binning the data, so that these average-locomotion plots are normalized against total activity events per hour. This behavioral rhythm (averaged for the 6 flies) shows two peaks, one at lights-on (0, 24, 48...), another at lights-off (12 hours later). The five luciferase rhythms exhibited early-morning peaks, albeit not all at identical times. Some of these molecular timecourses are smooth; others are noisy; and although some display high amplitudes while others do not, it is important to note that the strength of rhythmicity is obtained from the regularity of the data, not merely the amplitude of the oscillation. (b) Mean phase values determined for the entirety of the 144-hour (6-days) records in (a) are plotted over time for each whole-fly or dissected-specimen group. Note that the behavioral signal has been split into two components for this presentation: beh(m) is the morning peak near times of lights-on; beh(e), evening peak near lights-off. (c) Phase data in (b) re-plotted in polar coordinates on a unit circle. The direction of a given line extending from the center indicates the phase-time in hours, and the length of that line the consistency of the peak times over the 6-day timecourse. Whereas the average luciferase signals were quite consistent temporally (including on consecutive days), the behavioral peaks, especially the morning ones, were more variable.
Conclusions
We have presented a collection of methods for analyzing aspects of biological time series data across all modalities of data acquisition. Although we discuss the application of these tools to oscillating phenomena in one organism, they could as easily be applied to data involving other kinds of rhythms in any species. The collection of analytical processes we employed for evaluating rhythmicity and estimating period or phase represent, as far as we know, a unique aggregation of analytical tools for the analysis of biological data.
We were motivated to assemble this method for several reasons. First, it is likely that insights into the biology of circadian timing systems will emerge from the use of normalization procedures; this facilitates direct comparisons among behavioral, biochemical, molecular, and other signals – a possibility that has not been well-explored in the literature. Second, while some – but nowhere near all – of these tools are available in commercial packages, such products are expensive. More important, they proved unsatisfying to us, because such canned programs do not address the full range of temporally related questions one wishes to ask (and modifying these programs' code is usually not possible). Now that real-time, long-term methods are available to study molecular rhythms in mammalian tissues as well as in microbes, plants, and insects, methods such as ours will facilitate studies in a widening array of organisms.
Materials and Methods
Experimental data
All of the data used for analysis of luciferase activity in whole flies or body parts has been published previously [13].
Adult locomotor activity data are all presented here for the first time. Data used to assess the effects of trends (as depicted in Figure 3 and in the text) were collected using the Trikinetics Drosophila Activity Monitoring System (see below). In these experiments Canton-S males were reared in LD 12:12 at 25° C and collected as 2–3 day old young adults. These subjects were then moved into an incubator where they were placed in constant darkness; after 3 days they were loaded into the activity monitors under a dim red safe-light.
The experiments described in Table 1 employed Canton-S as a wild type control along with cyc01/+ [56] and cyc-deletion/+, a deficiency strain Df(3L)kto2 obtained from the Bloomington Stock Center. In these studies, 2–3 day old males were collected and loaded into the activity monitors. Locomotor activity rhythms were assessed in the incubator under LD 12:12 for either 5 or 6 days before the interval of constant darkness began (see Table 1).
Eclosion data were obtained from the wild type (Canton-S) using the Trikinetics system [65].
Heartbeat was recorded optically by placing a PI pupa on a temperature-controlled stage of a binocular microscope, one eyepiece of which was fitted with a phototransistor. Changes in illumination caused by the beating of the heart were registered by the phototransistor, amplified, and recorded directly on the disk of a desktop computer. The output is a direct plot of voltage as a function of time over a 30 s span of time [25].
Male mating song was recorded in an Insectavox [66] microphone system. A male previously housed to elicit maximal courtship was placed in the recording chamber with a female. Song was recorded directly through an AD converter into a microcomputer.
Data analysis system
Most of the analytical tools outlined below have been applied individually to previous Drosophila circadian rhythms data, most saliently MESA and autocorrelation were used in both behavioral and molecular studies [39, 15, 13]. Butterworth filters have been employed in studies of locomotor rhythms [13]. The Rhythmicity Index (RI) was devised to facilitate studies on Drosophila heart function behavioral studies [46, 25] and extended to the Drosophila luciferase assay [13]. Phase coherence and comparison analyses [32], have appeared in Yang et al. [17]. Cross correlation [37] has not been employed previously for the study of biological rhythms.
Input
The data files from eclosion and activity studies were generated using the Drosophila Activity Monitoring System (Trikinetics, Inc., Waltham MA) [for ex., [33]]. Data files generated by the DAM system provides a header to identify the name of the experiment, the location of the subject in the monitoring device, the date, the number of bins and the length of the bin in minutes. Immediately beneath this header, a string of numbers is arranged as a single column with the number of activity counts per bin listed for the duration of the experiment. In addition, there are special code numbers associated with being offline. These appear in place of the activity counts until the offline status has changed. These codes appear in association when the power goes down or a short circuit occurs in the system.
Our code reads these files by skipping the header and identifying any warning codes. We handle the occasional anomaly by using the average of the points on either side of the missing bin. In addition, the data are linked to a file that describes the lighting conditions (lights on or off) for each experiment, so that the data can be plotted (using data-display software newly written for this study) against a background with shading appropriate to the lighting condition.
The luciferase assay data were generated by a benchtop scintillation counter (Topcounter, Packard) [10, 18]. The Topcounter generates a file for each collection point that contains all the samples evaluated at that time; our code reorganizes this original data file such that a distinct record is retrieved for each sample (individual fly or tissue specimen dissected from it) with values listed in the order of occurrence from the beginning until the end of each experiment; the values are stored internally as a matrix whose columns represent individual subjects and whose rows represent observations at equally separated time frames.
The description given above applies typically to the files we analyze. However, there is nothing special about these files and we wish to emphasize that our analysis routines act on the matrix or data points we obtain from the data collection files. In principle then, the only barrier to analyzing data collected in any format is a way to read the data into a matrix and so our system could be easily adapted to other data collection schemes.
Processing
We used existing library functions (Matlab and Signal Processing Toolbox, Mathworks, Inc.) to implement the Butterworth filter, autocorrelation, crosscorrelation, and Fourier analyses. For these methods, we wrote functions to specify details such as the high and low frequency cutoffs with the filter, for example.
We wrote the code to analyze trends; to perform MESA; to identify peaks in the data and evaluate a phase shift by comparing two data sets; to plot such peaks around a circle and calculate mean vectors associated with a given set of peaks; to perform statistical tests on these vectors; to plot the data as shown above in Results and Discussion.
Output
In addition to numerical output associated with the analysis of a data set, all of the methods in our ensemble generate graphic output. We found this output to be an important part of our analytic process, in that looking at straightforward numerical outputs is a powerful aid to facilitate an intuitive understanding the results of the mathematical manipulations. At least for us, the statistical analysis is most meaningful when supported by what the human eye can infer (see text for more detail) from the graphical presentation of the data.
The phase plots and actograms are generated by functions written anew for this study. Actograms plot counts per bin as a histogram across the day. All of the actograms shown here are formatted as double plots with day 1 and day 2 on the first line, day 2 and day 3 on the second line and so on. These can be reformatted to change the daylength on the horizontal axis to the nearest increment defined by the sampling rate (for example, we can plot the data modulo...23.5 or 24.0 or 24.5 or..., when data are collected every 0.5 hours).
The present package was developed using MATLAB (Mathworks, Inc., Natick MA), version 5 and version 6, along with the Signal Processing tool box. While our code was written in Matlab, it could be adapted for use with similar products.
References
Pittendrigh CS: General Perspective. In: Handbook of Behavioral Neurobiology 4 Biological Rhythms. Edited by: J Aschoff. 1980, New York, Plenum Press, 57-77.
Dunlap JC: Molecular bases for circadian clocks. Cell. 1999, 96 (2): 271-90. 10.1016/S0092-8674(00)80566-8.
Gwinner E: Circadian and circannual programmes in avian migration. J Exptl Biol. 1996, 199: 39-48.
Hall JC: Genetics of biological rhythms in drosophila. Adv Genet. 1998, 38: 135-84.
Young MW: The molecular control of circadian behavioral rhythms and their entrainment in Drosophila. Annu Rev Biochem. 1998, 67: 135-52. 10.1146/annurev.biochem.67.1.135.
Williams JA, Sehgal A: Molecular components of the circadian system in drosophila. Ann. Rev. Physiol. 2001, 63: 729-755. 10.1146/annurev.physiol.63.1.729.
Allada R, Emery PE, Takahashi JS, Rosbash M: Stopping time: the genetics of fly and mouse circadian clocks. Ann. Rev. Neurosci. 2001, 24: 1091-119. 10.1146/annurev.neuro.24.1.1091.
Helfrich-Forster C, Stengl M, Homberg U: Organization of the circadian system in insects. Chronobiol Int. 1998, 15: 567-94.
Kaneko M: Neural substrates of Drosophila rhythms revealed by mutants and molecular manipulations. Curr Opin Neurobiol. 1998, 8 (5): 652-8. 10.1016/S0959-4388(98)80095-0.
Plautz J, Straume M, Stanewsky R, Jamison C, Brandes C, Dowse HB, Hall JC, Kay S: Quantitative analysis of Drosophila period gene transcription in living animals. J. Biol. Rhythms. 1997, 12: 204-217.
Krishnan B, Dryer SE, Hardin PE: Circadian rhythms in olfactory responses of Drosophila melanogaster. Nature. 1999, 400: 375-8. 10.1038/22566.
Giebultowicz JM, Stanewsky R, Hall JC, Hege DM: Transplanted Drosophila excretory tubules maintain circadian clock cycling out of phase with the host. Curr Biol. 2000, 10 (2): 107-10. 10.1016/S0960-9822(00)00299-2.
Krishnan B, Levine J, Sisson K, Dowse HB, Funes P, Hall JC, Hardin PE, Dryer SE: A new role for cryptochrome in a Drosophila circadian oscillator. Nature. 2001, 411: 313-317. 10.1016/S0014-5793(97)00747-3.
Hamblen M, Zehring WA, Kyriacou CP, Reddy P, Yu Q, Wheeler DA, Zwiebel LJ, Konopka RJ, Rosbash M, Hall JC: Germ-line transformation involving DNA from the period locus in Drosophila melanogaster: overlapping genomic fragments that restore circadian and ultradian rhythmicity to per0 and per-mutants. J Neurogenet. 1986, 3 (5): 249-91.
Wheeler DA, Hamblen-Coyle MJ, Dushay MS, Hall JC: Behavior in light-dark cycles of Drosophila mutants that are arrhythmic, blind, or both. J Biol Rhythms. 1993, 8 (1): 67-94.
Price JL, Blau J, Rothenfluh A, Abodeely M, Kloss B, Young" MW: double-time is a novel Drosophila clock gene that regulates PERIOD protein accumulation. Cell. 1998, 94: 83-95. 10.1016/S0092-8674(00)81224-6.
Yang Z, Emerson M, Su HS, Sehgal A: Response of the timeless protein to light correlates with behavioral entrainment and suggests a nonvisual pathway for circadian photoreception. Neuron. 1998, 21 (1): 215-23. 10.1016/S0896-6273(00)80528-0.
Stanewsky R, Jamison CF, Plautz JD, Kay SA, Hall JC: Multiple circadian-regulated elements contribute to cycling period gene expression in Drosophila. EMBO J. 1997, 16 (16): 5006-18. 10.1093/emboj/16.16.5006.
Kyriacou CP, Hall JC: Circadian rhythm mutations in Drosophila melanogaster affect short-term fluctuations in the male's courtship song. Proc Natl Acad Sci U S A. 1980, 77 (11): 6729-33.
Alt S, Ringo J, Talyn B, Bray W, Dowse H: The period gene controls courtship song cycles in Drosophila melanogaster. Anim. Behav. 1998, 56: 87-97. 10.1006/anbe.1998.0743.
Kyriacou CP, van den Berg MJ, Hall JC: Drosophila courtship song cycles in normal and period mutant males revisited. Behav. Genet. 1990, 20: 617-44.
Konopka RJ, Kyriacou CP, Hall JC: Mosaic analysis in the Drosophila CNS of circadian and courtship-song rhythms affected by a period clock mutation. J. Neurogenet. 1996, 11: 117-39.
Rizki T: The circulatory system and associated tissues. In: The genetics and biology of drosophila. Edited by: Ashburner M, T Wright. 1978, London, Academic Press, 397-452.
White L, Ringo J, Dowse HB: The effects of Deuterium Oxide and temperature on heart rate in Drosophila. J. Comp. Physiol. B. 1992, 162: 278-283.
Dowse HB, Ringo JM, Power J, Johnson E, Kinney K, White L: A congenital heart defect in Drosophila caused by an action potential mutation. J. Neurogenet. 1995, 10: 153-168.
Pierce JR: An introduction to information theory symbols, signals and noise. New York, Dover Publications, Inc. 1980
Dowse HB, Hall JC, Ringo JM: Circadian and ultradian rhythms in period mutants of Drosophila melanogaster. Behav. Genet. 1987, 17: 19-35.
Hamblen-Coyle M, Konopka RJ, Zweibel LJ, Colot HV, Dowse HB, Rosbash M, Hall JC: A new mutation at the period locus of Drosophila melanogaster with some novel effects on circadian rhythms. J. Neurogenet. 1989, 5: 229-56.
Dowse HB, Ringo JM: Do ultradian oscillators underlie the circadian clock in Drosophila?. In: Ultradian Rhythmicity in Biological Systems: An Inquiry into Fundamental Principles. Edited by: DL Lloyd E Rossi. 1992, New York, Springer Verlag, 105-117.
Dowse HB, Ringo JM: Is the biological clock a metaoscillator?. In: Molecular Approaches to Circadian Rhythms. Edited by: MW Young. 1993, New York, Marcel Dekker, 195-220.
Schwartz M, Shaw L: Signal Processing. New York: McGraw-Hill. 1975
Brandes C, Plautz JD, Stanewsky R, Jamison CF, Straume M, Wood KV, Kay SA, Hall JC: Novel features of drosophila period Transcription revealed by real-time luciferase reporting. Neuron. 1996, 16 (4): 687-92. 10.1016/S0896-6273(00)80088-4.
Stanewsky R, Kaneko M, Emery P, Beretta B, Wager-Smith K, Kay SA, Rosbash M, Hall JC: The cryb mutation identifies cryptochrome as a circadian photoreceptor in Drosophila. Cell. 1998, 95 (5): 681-92. 10.1016/S0092-8674(00)81638-4.
Hall JC: Cryptochromes: sensory reception, transduction, and clock functions subserving circadian systems. Curr Opin Neurobiol. 2000, 456-66. 10.1016/S0959-4388(00)00117-3. 4
Schefler WC: Statistics for the Biological Sciences. Reading, Massachusetts, Addison-Wesley. 1979
Hamming RW: Digital Filters. Englewood Cliffs, New Jersey, Prentice-Hall, Inc. 1983
Chatfield C: The analysis of time series. London, Chapman and Hall. 1980
Mercer DMA: Analytical methods for the study of periodic phenomena obscured by random fluctuations. Cold Spring Harbor Symposium on Quantitative Biology. 1960, 25: 73-86.
Dowse HB, Ringo JM: The search for hidden periodicities in biological time series revisited. J. Theor. Biol. 1989, 139: 487-515.
Johnson E, Bray N, Ringo J, Dowse HB: Genetic and pharmacological identification of ion channels central to the Drosophila cardiac pacemaker. J Neurogenet. 1998, 12: 1-24.
Enright JT: Data analysis. In: Handbook of Behavioral Neurobiology 4 Biological Rhythms. Edited by: J Aschoff. 1980, New York, Plenum Press, 21-38.
Whittaker E, Robinson G: The Calculus of Observations. Glasgow, Blackie and Son,. 1944
Kendall MG: Contributions to the Study of Oscillatory Time Series. London, Cambridge University Press. 1946
Dowse HB, Ringo JM: Comparisons between "periodograms" and spectral analysis: Apples are apples after all. J. Theoret. Biol. 1991, 148: 139-144.
Davis H: Fourier Series and Orthogonal Functions. Boston: Allyn and Bacon. 1963
Enright JT: Comparisons Between Periodograms and Spectral Analysis: Don't Expect Apples to taste like oranges. J Theor. Biol. 1990, 143: 425-430.
Power J, Ringo JM, Dowse HB: The effects of period mutations and light on the activity rhythms of Drosophila melanogaster. J. Biol. Rhythms. 1995, 10: 267-280.
Childers D: Modern spectrum analysis. New York: IEEE Press. 1978
Burg JP: Maximum entropy spectral analysis. Proc. 37th Meeting of the Society of Exploration Geophysicists. Edited by: Chiders. 1978, Modern Spectrum Analysis, New York: IEEE Press, 34-41.
Burg JP: A new analysis technique for time series data. NATO Advanced Study Institute on Signal Processing: Underwater Acoustics 1968 Reprinted. Edited by: Chiders. 1978, Modern Spectrum Analysis, New York: IEEE Press., 42-48.
Ulyrich T, Bishop T: Maximum entropy spectral analysis and autoregressive decomposition. Rev Geophys Space Phys. 1975, 13: 183-200.
Hicks KA, Millar AJ, Carre IA, Somers DE, Straume M, Meeks-Wagner DR, Kay SA: Conditional circadian dysfunction of the Arabidopsis early-flowering 3 mutant. Science. 1996, 274: 790-92. 10.1126/science.274.5288.790.
Kondo T, Strayer CA, Kulkarni RD, Taylor W, Ishiura M, Golden SS, Johnson CH: Circadian rhythms in prokaryotes: luciferase as a reporter of circadian gene expression in cyanobacteria Proc. Nat. Acad. Sci. USA. 1993, 90: 5672-5676.
Yamaguchi S, Kobayashi M, Mitsui S, Ishida Y, van der Horst GT, Suzuki M, Shibata S, Okamura H: View of a mouse clock gene ticking. Nature. 2001, 409 (6821): 684-10.1038/35055628.
Stokkan KA, Yamazaki S, Tei H, Sakaki Y, Menaker M: Entrainment of the circadian clock in the liver by feeding. Science. 2001, 291: 490-3. 10.1126/science.291.5503.490.
King DP, Zhao Y, Sangoram AM, Wilsbacher LD, Tanaka M, Antoch MP, Steeves TDL, Vitaterna MH, Kornhauser JM, Lowrey PL, Turek FW, Takahashi JS: Positional cloning of the mouse circadian clock gene. Cell. 1997, 89: 641-653. 10.1016/S0092-8674(00)80245-7.
Sokolove PG, Bushell WN: The chi square periodogram: its utility for analysis of circadian rhythms. J Theor Biol. 1978, 72: 131-60.
Rutila JE, Suri V, Le M, So WV, Rosbash M, Hall JC: CYCLE is a bHLH-PAS clock protein essential for circadian rhythmicity and transcription of Drosophila period and timeless. Cell. 1998, 93: 805-14. 10.1016/S0092-8674(00)81441-5.
Lindsley G, Dowse H, Burgoon P, Kilka M, Stephenson L: A persistent circhoral ultradian rhythm is identified in human core temperature. Chronobiology International. 1999, 16: 69-78.
Born M, Wolf E: Principles of Optics. Cambridge: Cambridge University Press. 1999, 7
Horne JH, Baliunas S: A prescription for period analysis of unevenly sampled time series. Astrophys. J. 1986, 320: 757-763. 10.1086/164037.
Aschoff J: Circadian Clocks. North Holland Publishing Co., Amsterdam,. 1965
Batschelet E: Statistical methods for the analysis of problems in animal orientation and certain biological rhythms. Washington DC, AIBS Monograph. 1965
Yang Z, Sehgal A: Role of molecular oscillations in generating behavioral rhythms in Drosophila. Neuron. 2001, 29: 453-67. 10.1016/S0896-6273(01)00218-5.
Konopka RJ, Hamblen-Coyle MJ, Jamison CF, Hall JC: An ultrashort clock mutation at the period locus of Drosophila melanogaster that reveals some new features of the fly's circadian system. J Biol Rhythms. 1994, 9: 189-216.
Gorczyka M, Hall J: The INSECTAVOX, and integrated device for recording and amplifying courship songs. Drosophila Information Service,. 1987, 66: 157-160.
Acknowledgements
The authors thank B. Talyn for her unpublished courtship song data, A. Pilgrim for her eclosion data, M. Mealey for her adult behavioral data used in analysis of phase response and OJ LeClair for her behavioral experiments used in the analysis of the cyc locus. We also thank John Ewer for his comments on the manuscript. This work was supported by grants to JCH from the US NIH (GM33205) and the US NIMH (MH51573).
Author information
Authors and Affiliations
Corresponding author
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Levine, J.D., Funes, P., Dowse, H.B. et al. Signal analysis of behavioral and molecular cycles. BMC Neurosci 3, 1 (2002). https://doi.org/10.1186/1471-2202-3-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1471-2202-3-1