Abstract
In this paper, we define and study some new subclasses of starlike and close-to-convex functions with respect to symmetrical points. These functions map the open unit disc onto certain conic regions in the right half plane. Some basic properties, a necessary condition, and coefficient and arc length problems are investigated. The mapping properties of the functions in these classes are studied under a certain linear operator.
MSC:30C45, 30C50.
Similar content being viewed by others
1 Introduction
Let A be the class of functions of the form
which are analytic in the open unit disc . Let S, K, , and C be the subclasses of A which consist of univalent, close-to-convex, starlike (with respect to origin), and convex functions, respectively. For recent developments, extensions, and applications, see [1–25] and the references therein.
A function f in A is said to be uniformly convex in E if f is a univalent convex function along with the property that, for every circular arc γ contained in E, with center ξ also in E, the image curve is a convex arc. The class of uniformly convex functions is denoted by . The corresponding class is defined by the relation that if, and only if, . It is well known [13] that if, and only if
Uniformly starlike and convex functions were first introduced by Goodman [3] and then studied by various other authors. If , we say f is subordinate to g in E, written as or , if there exists a Schwarz function such that for .
For , the class consists of functions analytic in E with such that for , and, with , we obtain the well-known class P of Carathéodory functions with positive real part.
For , the conic regions are defined as follows, see [5]:
For fixed k, represents the conic regions bounded, successively, by the imaginary axis (), the right branch of a hyperbolic () and a parabola (). When , the domain becomes a bounded domain being the interior of the ellipse.
We shall consider the case when . Related to the domain , the following functions , , play the role of extremal functions mapping in E onto :
These functions are univalent in E and belong to the class P. Using the subordination concept, we define the class as follows.
Let be analytic in E with . Then if, and only if, in E and are given by (1.2).
The conic domains can be generalized as given by
with the corresponding extremal function
It can easily be seen that the analytic function , with , belongs to the class if in E.
It is easy to verify that is a convex set. It is known [6] that
and, for , we have
where
So we can write , .
Also
Sakaguchi [24] introduced and studied the class of starlike functions with respect to symmetrical points. The class includes the classes of convex and odd starlike functions with respect to the origin. It was shown [24] that a necessary and sufficient condition for to be univalent and starlike with respect to symmetrical points in E is that
Das and Singh [2] defined the classes of convex functions with respect to symmetrical points and showed that a necessary and sufficient condition for is that
It is also well known [2] that if, and only if, .
We now define the following.
Definition 1.1 Let . The f is said to be in the class if, and only if,
It can easily be seen that
Also, for , the class reduces to .
The class is defined as follows.
Definition 1.2 Let . Then if, and only if for .
We note that
Definition 1.3 Let . Then if, and only if, there exists such that
Since , , and , we note that
where consists of close-to-convex functions with respect to symmetrical starlike functions.
From the definition, it is clear that consists of univalent functions.
For , and , reduces to the class .
2 Preliminary results
We shall need the following lemmas to prove our main results.
Lemma 2.1 [15]
Let be a convex function in E with and let another function be with . Let be analytic in E with such that
Then , .
Lemma 2.2 Let , be analytic in E with
and let for . Then implies that for .
Proof Let
Then
where
Since , we have
We now use Lemma 2.1 and this implies that
This proves that for . □
The following lemma is an easy extension of a result proved in [5].
Lemma 2.3 Let and , be any complex numbers with and let . If is analytic in E, and it satisfies
and is an analytic solution of
then is univalent and
and is the best dominant of (2.1).
3 The class
In this section, we shall study some basic properties of the class .
Theorem 3.1 Let . Then the odd function
belongs to in E.
In particular is an odd starlike function of order in E.
Proof Logarithmic differentiation of (3.1) and simple computation yield
Since is a convex set, it follows that and thus in E. □
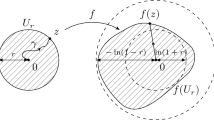
As a special case, we note that, for , in E, and hence . We now discuss a geometric property for . Here we investigate the behavior of the inclusion of the tangent at a point to the image of the circle , , , under the mapping by means of a function f from the class .
Let
and, for , ,
Now, since
then
Hence
Also, on the other hand,
So, the integral on the left side of the last inequality characterizes the increment of the angle of the inclination of the tangent to the curve between the points and for .
We have the following necessary condition for .
Theorem 3.2 Let . Then, with and , and , we have
where σ is given by (1.3) and .
Proof Since , and .
We can write
and this gives us, with , , ,
For , we observe that
Therefore
and
We can write
and for , it is well known that
From this, we have
Thus the values of h are contained in the circle of Apollonius whose diameter is the line segment from to and has the radius . So attains its maximum at points where a ray from origin is tangent to the circle, that is, when
From (3.3), we observe that
Also, for ,
Using (3.4) and (3.5) in (3.2), we obtain the required result. □
We note the following special cases:
-
1.
For , , , it follows from Theorem 3.2 that
This is a necessary and sufficient condition for f to be close-to-convex (hence univalent) in E; see [7]. This also shows that .
-
2.
For .
-
3.
When , it is obvious that . In this case, the class consists of strongly close-to-convex functions of order σ in the sense of Pommerenke [20, 21].
Theorem 3.3 (Integral representation)
Let . Then
where , .
Proof Since , we can write
This gives us
and the result follows when we integrate. □
When , , we obtain the result for the class given in [5].
We now study the class under a certain integral operator.
Theorem 3.4 Let and let for be defined by
Then belongs to in E.
Proof Let
Since , , and . Therefore it can easily be verified that is -valently starlike in E.
We can write (3.6) as
and, differentiating logarithmically, we have
say, where and D is -valently starlike.
Let
Then
Since
We now apply Lemma 2.2 to obtain
This proves that in E. □
Theorem 3.5 Let and let F be defined by the following integral operator:
where , , and . Then belongs to for .
When , , we obtain a generalized form of the Bernardi operator; see [1]. Also for , , and , we have the well-known integral operator studied by Libera [11] who showed that it preserves the geometric properties of convexity, starlikeness, and close-to-convexity.
Proof Let , . Then in E. We can write (3.8) as
Differentiating (3.9) logarithmically, and with , we have
Since, for , , , both belong to in E, and is a convex set. Therefore
From (3.10) and (3.11), it follows that
We now apply Lemma 2.3 which gives us
Thus and the proof is complete. □
4 The class
Here we shall study some properties of the class which consists of k-uniformly close-to-convex functions.
Let denote the length of the image of the circle under f. We prove the following.
Theorem 4.1 Let . Then, for , ,
where and σ is given by (1.3), and is a constant depending only on k, β.
Proof For , we can write
and , .
Since and is odd, there exists an odd starlike function such that
Thus, with ,
and using Hölder’s inequality, we have
For , it is well known [20] that
Using (4.3) and subordination for odd starlike functions in (4.2), it follows that
where C and are constants depending only on and σ. This completes the proof. □
We now discuss the growth rate of coefficients of .
Theorem 4.2 Let and be given by (1.1). Then
where is a constant depending only on σ and and σ, are as given in Theorem 4.1.
Proof For , , Cauchy’s Theorem gives us
With , we use Theorem 4.1 and obtain the required result. □
Theorem 4.3 Let and let F be defined by
Then in E. That is, the class is preserved under the integral operator (4.4).
Proof Since , we can write
Let and be defined by (3.5). By Theorem 3.4, and . Let . Then we can write
Thus, from (4.4) and , , we have
say. We note that , and for ,
Since is a convex set, in E. We thus have
Now, using Lemma 2.2, it follows that
This proves that in E. □
We study a partial converse of the above result as follows.
Theorem 4.4 Let in E and let
Then for , where
Proof We shall need the following well-known results for , ; see [4]:
Since , there exists such that, for .
From (4.5), we have
and this gives us
where
Now, using (4.7) and (4.8), we have
where
We note that and . So there exists . The right hand side of (4.9) is positive for , where is given by (4.6). This implies that for and the proof is complete. □
We have the following special cases.
-
1.
For , . Then , defined by (4.5) belongs to for .
-
2.
When and (that is, ), then belongs to the same class for . This result has been proved by Livingston [12] for convex and starlike functions.
References
Bernardi SD: Convex and starlike univalent functions. Trans. Am. Math. Soc. 1969, 135: 429-446.
Das RN, Singh P: On subclasses of Schlicht mappings. Indian J. Pure Appl. Math. 1977, 8: 864-872.
Goodman AW: On uniformly starlike functions. J. Math. Anal. Appl. 1991, 155: 364-370. 10.1016/0022-247X(91)90006-L
Goodman AW: Univalent Functions, Vol I & II. Polygonal Publishing House, Washington; 1983.
Kanas S: Differential subordination related to conic sections. J. Math. Anal. Appl. 2006,317(2):650-658. 10.1016/j.jmaa.2005.09.034
Kanas S: Techniques of differential subordination for domains bounded by conic sections. Int. J. Math. Math. Sci. 2003, 38: 2389-2400.
Kanas S, Lecko A, Moleda A: Certain generalization of the Sakaguchi lemma. Folia Sci. Univ. Tech. Resov. 1987, 38: 35-42.
Kanas S, Sugawa T: On conformal representation of the interior of an ellipse. Ann. Acad. Sci. Fenn., Math. 2006, 31: 329-348.
Kanas S, Wisniowska A: Conic regions and k-uniform convexity. J. Comput. Appl. Math. 1999, 105: 327-336. 10.1016/S0377-0427(99)00018-7
Kaplan W: Close-to-convex Schlicht functions. Mich. Math. J. 1952, 1: 169-185.
Libera RJ: Some classes of regular univalent functions. Proc. Am. Math. Soc. 1965, 16: 755-758. 10.1090/S0002-9939-1965-0178131-2
Livingston AE: On the radius of univalence of certain analytic functions. Proc. Am. Math. Soc. 1966, 17: 352-359. 10.1090/S0002-9939-1966-0188423-X
Ma W, Minda D: Uniformly convex functions. Ann. Pol. Math. 1992,57(2):165-175.
Ma W, Minda D: Uniformly convex functions II. Ann. Pol. Math. 1992,58(3):275-285.
Miller SS, Mocanu PT: Univalent solution of Briot-Bouquet differential equations. J. Differ. Equ. 1985, 56: 297-308. 10.1016/0022-0396(85)90082-8
Noor KI, Noor MA: Higher order close-to-convex functions related with conic domain. Appl. Math. Inf. Sci. 2014,8(5):2455-2463. 10.12785/amis/080541
Noor, KI, Ahmad, QZ, Noor, MA: On some subclasses of analytic functions defined by fractional derivative in the conic regions. Appl. Math. Inf. Sci. (2014/15)
Noor KI, Fayyaz R, Noor MA: Some classes of k -uniformly functions with bounded radius rotation. Appl. Math. Inf. Sci. 2014,8(2):1-7.
Noor, KI, Noor, MA, Murtaza, R: Inclusion properties with applications for certain subclasses of analytic functions. Appl. Math. Inf. Sci. (2014/15)
Pommerenke C: On close-to-convex analytic functions. Trans. Am. Math. Soc. 1965, 14: 176-186.
Pommerenke C: On starlike and close-to-convex functions. Proc. Lond. Math. Soc. 1963, 3: 290-304.
Ronning F: On starlike functions associated with parabolic regions. Ann. Univ. Mariae Curie-Skłodowska, Sect. A 1991, 45: 117-122.
Ronning F: Uniformly convex functions and a corresponding class of starlike functions. Proc. Am. Math. Soc. 1993, 118: 189-196. 10.1090/S0002-9939-1993-1128729-7
Sakaguchi K: On a certain univalent mapping. J. Math. Soc. Jpn. 1959, 11: 72-73. 10.2969/jmsj/01110072
Stankiewicz J: Some remarks on functions starlike with respect to symmetrical points. Ann. Univ. Mariae Curie-Skłodowska. Sect. A 1965, 19: 53-59.
Acknowledgements
The author would like to thank editor and anonymous referee for their valuable suggestions. The author is grateful to Dr. SM Junaid Zaidi, Rector, COMSATS Institute of Information Technology, Pakistan for providing an excellent research and academic environment. This research is supported by HEC NRPU project No: 20-1966/R&D/11-2553, titled, Research unit od Academic Excellence in Geometric Function Theory and Applications.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that she has no competing interest.
Author’s contributions
The article is the work of one author, who read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Noor, K.I. On uniformly univalent functions with respect to symmetrical points. J Inequal Appl 2014, 254 (2014). https://doi.org/10.1186/1029-242X-2014-254
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2014-254