Abstract
In this paper, we establish dislocated quasi-b-metric spaces and introduce the notions of Geraghty type dqb-cyclic-Banach contraction and dqb-cyclic-Kannan mapping and derive the existence of fixed point theorems for such spaces. Our main theorem extends and unifies existing results in the recent literature.
Similar content being viewed by others
1 Introduction and preliminaries
Fixed point theory has been studied extensively, which can be seen from the works of many authors [1–6]. Banach contraction principle was introduced in 1922 by Banach [7] as follows:
-
(i)
Let \((X,d)\) be a metric space and let \(T:X\to X\). Then T is called a Banach contraction mapping if there exists \(k\in[0, 1)\) such that
$$d(Tx,Ty)\leq k d(x,y) $$for all \(x, y \in X\).
The concept of Kannan mapping was introduced in 1969 by Kannan [8] as follows:
-
(ii)
T is called a Kannan mapping if there exists \(r\in[0, \frac{1}{2})\) such that
$$d(Tx, Ty) \leq r d(x,Tx) + r d(y, Ty) $$for all \(x, y \in X\).
Now, we recall the definition of cyclic map. Let A and B be nonempty subsets of a metric space \((X,d)\) and \(T: A\cup B\to A\cup B\). T is called a cyclic map iff \(T(A)\subseteq B\) and \(T(B)\subseteq A\).
In 2003, Kirk et al. [9] introduced cyclic contraction as follows:
-
(iii)
A cyclic map \(T: A\cup B\to A\cup B\) is said to be a cyclic contraction if there exists \(a\in[0, 1)\) such that
$$d(Tx,Ty)\leq a d(x,y) $$for all \(x\in A\) and \(y\in B\).
In 2010, Karapinar and Erhan [10] introduced Kannan type cyclic contraction as follows:
-
(iv)
A cyclic map \(T: A\cup B\to A\cup B\) is called a Kannan type cyclic contraction if there exists \(b\in[0, \frac{1}{2})\) such that
$$d(Tx, Ty) \leq bd(x,Tx) + b d(y, Ty) $$for all \(x\in A\) and \(y\in B\).
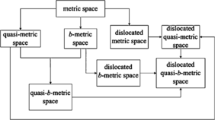
If \((X,d)\) is a complete metric space, at least one of (i), (ii), (iii) and (iv) holds, then it has a unique fixed point [7–10]. Next, we discuss the development of spaces. The concept of quasi-metric spaces was introduced by Wilson [11] in 1931 as a generalization of metric spaces, and in 2000 Hitzler and Seda [12] introduced dislocated metric spaces as a generalization of metric spaces, [13] generalized the result of Hitzler, Seda and Wilson and introduced the concept of dislocated quasi-metric space. Włodarczyk et al. (see [14–21]) created uniform spaces as this is the concept of metric spaces. In 1989, Bakhtin [22] introduced b-metric space as a generalization of metric space. Moreover, Czerwik [23] made the results of Bakhtin known more in 1998. Finally, many other generalized b-metric spaces such as quasi-b-metric spaces [24], b-metric-like spaces [25] and quasi-b-metric-like spaces [26] were introduced.
We begin with the following definition as a recall from [11, 12].
Definition 1.1
Let X be a nonempty set. Suppose that the mapping \(d: X\times X\rightarrow [0,\infty)\) satisfies the following conditions:
- (d1):
-
\(d(x,x)=0\) for all \(x\in X\);
- (d2):
-
\(d(x,y)=d(y,x)=0\) implies \(x=y\) for all \(x,y\in X\);
- (d3):
-
\(d(x,y)=d(y,x)\) for all \(x,y\in X\);
- (d4):
-
\(d(x,y)\leq[d(x,z)+d(z,y)]\) for all \(x,y,z\in X\).
If d satisfies conditions (d1), (d2) and (d4), then d is called a quasi-metric on X. If d satisfies conditions (d2), (d3) and (d4), then d is called a dislocated metric on X. If d satisfies conditions (d1)-(d4), then d is called a metric on X.
In 2005 the concept of dislocated quasi-metric spaces [13], which is a new generalization of quasi-b-metric spaces and dislocated b-metric spaces, was introduced. By Definition 1.1, if setting conditions (d2) and (d4) hold true, then d is called a dislocated quasi-metric on X.
Remark 1.2
It is obvious that metric spaces are quasi-metric spaces and dislocated metric spaces, but the converse is not true.
In 1989, Bakhtin [22] introduced the concept of b-metric spaces and investigated some fixed point theorems in such spaces.
Definition 1.3
[22]
Let X be a nonempty set. Suppose that the mapping \(b: X\times X\rightarrow[0,\infty)\) such that the constant \(s\geq1\) satisfies the following conditions:
- (b1):
-
\(b(x,y)=b(y,x)=0 \Leftrightarrow x=y\) for all \(x,y\in X\);
- (b2):
-
\(b(x,y)=b(y,x)\) for all \(x,y\in X\);
- (b3):
-
\(b(x,y)\leq s[b(x,z)+b(z,y)]\) for all \(x,y,z\in X\).
The pair \((X, b)\) is then called a b-metric space.
Remark 1.4
It is obvious that metric spaces are b-metric spaces, but conversely this is not true.
In 2012, Shah and Hussain [24] introduced the concept of quasi-b-metric spaces and verified some fixed point theorems in quasi-b-metric spaces.
Definition 1.5
[24]
Let X be a nonempty set. Suppose that the mapping \(q: X\times X\rightarrow[0,\infty)\) such that constant \(s\geq1\) satisfies the following conditions:
- (q1):
-
\(q(x,y)=q(y,x)=0 \Leftrightarrow x=y\) for all \(x,y\in X\);
- (q2):
-
\(q(x,y)\leq s[q(x,z)+q(z,y)]\) for all \(x,y,z\in X\).
The pair \((X, q)\) is then called a quasi-b-metric space.
Remark 1.6
It is obvious that b-metric spaces are quasi-b-metric spaces, but conversely this is not true.
Recently, the concept of b-metric-like spaces, which is a new generalization of metric-like spaces, was introduced by Alghamdi et al. [25].
Definition 1.7
[25]
Let X be a nonempty set. Suppose that the mapping \(D: X\times X\rightarrow[0,\infty)\) such that constant \(s\geq1\) satisfies the following conditions:
- (D1):
-
\(D(x,y)=0 \Rightarrow x=y\) for all \(x,y\in X\);
- (D2):
-
\(D(x,y)=D(y,x)\) for all \(x,y\in X\);
- (D3):
-
\(D(x,y)\leq s[D(x,z)+D(z,y)]\) for all \(x,y,z\in X\).
The pair \((X, D)\) is then called a b-metric-like space (or a dislocated b-metric space).
Remark 1.8
It is obvious that b-metric spaces are b-metric-like spaces, but conversely this is not true.
In this paper we introduce dislocated quasi-b-metric spaces which generalize quasi-b-metric spaces and b-metric-like spaces, and we introduce the notions of Geraghty type dqb-cyclic-Banach contraction and dqb-cyclic-Kannan mapping and derive the existence of fixed point theorems for such spaces. Our main theorems extend and unify existing results in the recent literature.
2 Main results
In this section, we begin with introducing the notion of dislocated quasi-b-metric space.
Definition 2.1
Let X be a nonempty set. Suppose that the mapping \(d: X\times X\rightarrow[0,\infty)\) such that constant \(s\geq 1\) satisfies the following conditions:
-
(d1)
\(d(x,y)=d(y,x)=0\) implies \(x=y\) for all \(x,y\in X\);
-
(d2)
\(d(x,y)\leq s[d(x,z)+d(z,y)]\) for all \(x,y,z\in X\).
The pair \((X, d)\) is then called a dislocated quasi-b-metric space (or simply dqb-metric). The number s is called the coefficient of \((X, d)\).
Remark 2.2
It is obvious that b-metric spaces, quasi-b-metric spaces and b-metric-like spaces are dislocated quasi-b-metric spaces, but the converse is not true.
Example 2.3
Let \(X=\mathbb{R}\) and let
where \(n,m \in\mathbb{N}\setminus\{1\}\) with \(n\neq m\).
Then \((X, d)\) is a dislocated quasi-b-metric space with the coefficient \(s =2\), but since \(d(1, 1) \neq 0\), we have \((X, b)\) is not a quasi-b-metric space, and since \(d(1, 2) \neq d(2, 1) \), we have \((X, b)\) is not a b-metric-like space. And \((X, b)\) is not a dislocated quasi-metric space. Indeed, let \(x,y,z\in X\). Suppose that \(d(x,y)=0\).
Then
It implies that \(|x-y|^{2}=0\), and so \(x=y\).
Next, consider
where \(s=2\),
where \(n,m>42\).
Example 2.4
[26]
Let \(X = \{0, 1, 2\}\), and let \(d: X\times X\to\mathbb{R}^{+}\) be defined by
Then \((X, d)\) is a dislocated quasi-b-metric space with the coefficient \(s =2\), but since \(d(1, 1) \neq 0\), we have \((X, b)\) is not a quasi-b-metric space, and since \(d(1, 2) \neq d(2, 1) \), we have \((X, b)\) is not a b-metric-like space. It is obvious that \((X, b)\) is not a dislocated quasi-metric space.
Example 2.5
Let \(X=\mathbb{R}\) and let
Then \((X, d)\) is a dislocated quasi-b-metric space with the coefficient \(s =2\), but since \(d(0, 1) \neq d(1, 0)\), we have \((X, b)\) is not a b-metric-like space, since \(d(1, 1) \neq 0\), we have \((X, b)\) is not a quasi-b-metric space. It is obvious that \((X, b)\) is not a dislocated quasi-metric space.
Example 2.6
Let \(X=\mathbb{R}\) and let
Then \((X, d)\) is a dislocated quasi-b-metric space with the coefficient \(s =2\), but since \(d(1, 1) \neq 0\), we have \((X, b)\) is not a quasi-b-metric space. It is obvious that \((X, b)\) is not a dislocated quasi-metric space.
We will introduce a dislocated quasi-b-convergent sequence, a Cauchy sequence and a complete space according to Zoto et al. [27].
Definition 2.7
-
(1)
A sequence \((\{x_{n}\})\) in a dqb-metric space \((X,d)\) dislocated quasi-b-converges (for short, dqb-converges) to \(x\in X\) if
$$\lim_{n\to\infty}d(x_{n},x)=0=\lim_{n\to\infty}d(x,x_{n}). $$In this case x is called a dqb-limit of \((\{x_{n}\})\), and we write \((x_{n}\to x)\).
-
(2)
A sequence \((\{x_{n}\})\) in a dqb-metric space \((X,d)\) is called Cauchy if
$$\lim_{n,m\to\infty}d(x_{n},x_{m})=0=\lim _{n,m\to\infty}d(x_{m},x_{n}). $$ -
(3)
A dqb-metric space \((X,d)\) is complete if every Cauchy sequence in it is dqb-convergent in X.
Next, we begin with introducing the concept of a dqb-cyclic-Banach contraction.
Definition 2.8
Let A and B be nonempty subsets of a dislocated quasi-b-metric space \((X,d)\). A cyclic map \(T: A\cup B\to A\cup B\) is said to be a dqb-cyclic-Banach contraction if there exists \(k\in [0, 1)\) such that
for all \(x\in A\), \(y\in B\) and \(s\geq1\) and \(sk \leq1\).
Now we prove our main results.
Theorem 2.9
Let A and B be nonempty subsets of a complete dislocated quasi-b-metric space \((X,d)\). Let T be a cyclic mapping that satisfies the condition of a dqb-cyclic-Banach contraction. Then T has a unique fixed point in \(A\cap B \).
Proof
Let \(x\in A (\mathrm{fix})\) and, using the contractive condition of the theorem, we have
and
So,
and
where \(\alpha=\max\{d(Tx,x),d(x,Tx)\}\).
By using (2.2) and (2.3), we have \(d(T^{3}x,T^{2}x)\leq k^{2}\alpha\), and \(d(T^{2}x,T^{3}x)\leq k^{2}\alpha\).
For all \(n\in\mathbb{N}\), we get
and
Let \(n,m\in\mathbb{N}\) with \(m>n\), by using the triangular inequality, we have
for some \(\xi>m-n+1\).
Take \(n\to\infty\), we get \(d(T^{m}x,T^{n}x)\to0\).
Similarly, let \(n,m\in\mathbb{N}\) with \(m>n\), by using the triangular inequality, we have
Take \(n\to\infty\), we get \(d(T^{n}x,T^{m}x)\to0\). Thus \(T^{n}x\) is a Cauchy sequence.
Since \((X,d)\) is complete, we have \(\{T^{n}x\}\) converges to some \(z\in X\).
We note that \(\{T^{2n}x\}\) is a sequence in A and \(\{T^{2n-1}x\}\) is a sequence in B in a way that both sequences tend to the same limit z.
Since A and B are closed, we have \(z\in A\cap B\), and then \(A\cap B\neq{\emptyset}\).
Now, we will show that \(Tz=z\).
By using (2.1), consider
Taking limit as \(n\to\infty\) in the above inequality, we have
And so \(d(z,Tz)=kd(z,Tz)\), where \(0\leq k<1\). This implies that \(d(z,Tz)=0\).
Similarly, considering form (2.1), we get
Taking limit as \(n\to\infty\) in the above inequality, we have
And so \(d(Tz,z)=kd(Tz,z)\), where \(0\leq k<1\). This implies that \(d(Tz,z)=0\).
Hence \(d(z,Tz)=d(Tz,z)=0\), this implies that \(Tz=z\), that is, z is a fixed point of T.
Finally, to prove the uniqueness of a fixed point, let \(z^{*}\in X\) be another fixed point of T such that \(Tz^{*}=z^{*}\).
Then we have
On the other hand,
By forms (2.4) and (2.5), we obtain that \(d(z,z^{*})=d(z^{*},z)=0\), this implies that \(z^{*}=z\).
Therefore z is a unique fixed point of T. This completes the proof. □
Example 2.10
Let \(X=[-1,1]\) and \(T: A\cup B\to A\cup B\) defined by \(Tx=\frac{-x}{5}\). Suppose that \(A=[-1,0]\) and \(B=[0,1]\). Define the function \(d:X^{2}\to[0,\infty)\) by
We see that d is a dislocated quasi-b-metric on X.
Now, let \(x\in A\). Then \(-1\leq x\leq0\). So, \(0\leq\frac{-x}{5}\leq \frac{1}{5}\). Thus, \(Tx\in B\).
On the other hand, let \(x\in B\). Then \(0\leq x\leq1\). So, \(\frac {-1}{5}\leq\frac{-x}{5}\leq0\). Thus, \(Tx\in A\).
Hence the map T is cyclic on X because \(T(A)\subset B\) and \(T(B)\subset A\).
Next, we consider
so for \(\frac{1}{5}\leq k<1\).
Thus T satisfies the dqb-cyclic-Banach contraction of Theorem 2.9 and 0 is the unique fixed point of T.
Finally, we begin with introducing the concept of dqb-cyclic-Kannan mapping.
Definition 2.11
Let A and B be nonempty subsets of a dislocated quasi-b-metric space \((X,d)\). A cyclic map \(T: A\cup B\to A\cup B\) is called a dqb-cyclic-Kannan mapping if there exists \(r\in[0, \frac{1}{2})\) such that
for all \(x\in A\), \(y\in B\) and \(s\geq1\) and \(sr \leq\frac{1}{2}\).
In the next theorem, we will prove the fixed point theorem for a cyclic-Kannan mapping in a dislocated quasi-b-metric space.
Theorem 2.12
Let A and B be nonempty subsets of a complete dislocated quasi-b-metric space \((X,d)\). Let T be a cyclic mapping that satisfies the condition of a dqb-cyclic-Kannan mapping. Then T has a unique fixed point in \(A\cap B \).
Proof
Let \(x\in A (\mathrm{fix})\) and, using the contractive condition of the theorem, we have
so
And from (2.7) we have
so
where \(\beta=2d(x,Tx)\).
By using (2.7) and (2.8), we have
and
For all \(n\in\mathbb{N}\), we get
and
Let \(n,m\in\mathbb{N}\) with \(m>n\), by using the triangular inequality, we have
for some \(\xi>m-n+1\). Take \(n\to\infty\), we get \(d(T^{m}x,T^{n}x)\to0\).
Similarly, let \(n,m\in\mathbb{N}\) with \(m>n\), by using the triangular inequality, we have
Take \(n\to\infty\), we get \(d(T^{n}x,T^{m}x)\to0\). Thus \(T^{n}x\) is a Cauchy sequence.
Since \((X,d)\) is complete, we have \(\{(T^{n}x)\}\) converges to some \(z\in X\).
We note that \(\{T^{2n}x\}\) is a sequence in A and \(\{T^{2n-1}x\}\) is a sequence in B in a way that both sequences tend to the same limit z.
Since A and B are closed, we have \(z\in A\cap B\), and then \(A\cap B\neq{\emptyset}\).
Now, we will show that \(Tz=z\).
By using (2.6), consider
Taking limit as \(n\to\infty\) in the above inequality, we have
Since \(0\leq r<\frac{1}{2}\), we have \(d(z,Tz)=0\).
Similarly, considering form (2.6), we get
Taking limit as \(n\to\infty\) in the above inequality, we have
Since \(d(z,Tz)=0\), we have \(d(z,Tz)=0\).
Hence \(d(z,Tz)=d(Tz,z)=0 \Rightarrow Tz=z\) and z is a fixed point of T.
Finally, to prove the uniqueness of a fixed point, let \(z^{*}\in X\) be another fixed point of T such that \(Tz^{*}=z^{*}\).
Then we have \(d(z,z) =d(z^{*},z^{*})=0\), because by assumption
On the other hand,
By forms (2.9) and (2.10), we obtain that \(d(z,z^{*})=d(z^{*},z)=0 \Rightarrow z^{*}=z\).
Therefore z is a unique fixed point of T. This completes the proof. □
Example 2.13
Let \(X=[-1,1]\) and \(T:X\to X\) defined by \(Tx=\frac{-x}{7}\). Suppose that \(A=[-1,0]\) and \(B=[0,1]\). Define the function \(d:X^{2}\to[0,\infty)\) by
We see that d is a dislocated quasi-b-metric on X.
Now, let \(x\in A\). Then \(-1\leq x\leq0\). So, \(0\leq\frac{-x}{7}\leq\frac{1}{7}\). Thus, \(Tx\in B\).
On the other hand, let \(x\in B\). Then \(0\leq x\leq1\). So, \(\frac {-1}{7}\leq\frac{-x}{7}\leq0\). Thus, \(Tx\in A\).
Hence the map T is cyclic on X because \(T(A)\subset B\) and \(T(B)\subset A\).
Next, we consider
so for \(\frac{2}{23}\leq r<\frac{1}{2}\).
Thus T satisfies the dqb-cyclic-Banach contraction of Theorem 2.12 and 0 is the unique fixed point of T.
References
Basha, SS, Veeramani, P: Best proximity pair theorems for multifunctions with open fibres. J. Approx. Theory 103, 119-129 (2000)
Enjouji, Y, Nakanishi, M, Suzuki, T: A generalization of Kannan’s fixed point theorem. Fixed Point Theory Appl. 2009, Article ID 192872 (2009)
Kikkawa, M, Suzuki, T: Some similarity between contractions and Kannan mappings. Fixed Point Theory Appl. 2008, Article ID 649749 (2008)
Nakanishi, M, Suzuki, T: An observation on Kannan mappings. Cent. Eur. J. Math. 8, 170-178 (2010)
Reich, S: Kannan’s fixed point theorem. Boll. Unione Mat. Ital. 4, 1-11 (1971)
Shioji, N, Suzuki, T, Takahashi, W: Contractive mappings, Kannan mappings and metric completeness. Proc. Am. Math. Soc. 126, 3117-3124 (1998). doi:10.1090/S0002-9939-98-04605-X
Banach, S: Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 3, 133-181 (1922)
Kannan, R: Some results on fixed points - II. Am. Math. Mon. 76, 405-408 (1969)
Kirk, WA, Srinivasan, PS, Veeramani, P: Fixed points for mapping satisfying cyclic contractive conditions. Fixed Point Theory 4, 79-89 (2003)
Karapinar, E, Erhan, IM: Best proximity on different type contractions. Appl. Math. Inf. Sci. 5, 558-569 (2010)
Wilson, WA: On quasi-metric spaces. Am. J. Math. 53(3), 675-684 (1931)
Hitzler, P, Seda, A: Dislocated topologies. J. Electr. Eng. 51, 3-7 (2000)
Zeyada, FM, Hassan, GH, Ahmad, MA: A generalization of fixed point theorem due to Hitzler and Seda in dislocated quasi-metric space. Arab. J. Sci. Eng. 31, 111-114 (2005)
Włodarczyk, K, Plebaniak, R, Banach, A: Best proximity points for cyclic and noncyclic set-valued relatively quasi-asymptotic contractions in uniform spaces. Nonlinear Anal. 70, 3332-3341 (2009)
Włodarczyk, K, Plebaniak, R, Banach, A: Erratum to: ‘Best proximity points for cyclic and noncyclic set-valued relatively quasi-asymptotic contractions in uniform spaces’. Nonlinear Anal. 71, 3585-3586 (2009)
Włodarczyk, K, Plebaniak, R, Obczyłski, C: Convergence theorems, best approximation and best proximity for set-valued dynamic systems of relatively quasi-asymptotic contractions in cone uniform spaces. Nonlinear Anal. 72, 794-805 (2010)
Włodarczyk, K, Plebaniak, R: Kannan-type contractions and fixed points in uniform spaces. Fixed Point Theory Appl. 2011, 90 (2011)
Włodarczyk, K, Plebaniak, R: Contractions of Banach, Tarafdar, Meir-Keller, Ćirić-Jachymski-Matkowski and Suzuki types and fixed points in uniform spaces with generalized pseudodistances. J. Math. Anal. Appl. 404, 338-350 (2013)
Włodarczyk, K, Plebaniak, R: Asymmetric structures, discontinuous contractions and iterative approximation of fixed and periodic points. Fixed Point Theory Appl. 2013, 128 (2013)
Włodarczyk, K: Hausdorff quasi-distances, periodic and fixed points for Nadler type set-valued contractions in quasi-gauge spaces. Fixed Point Theory Appl. 2013, 239 (2013)
Włodarczyk, K, Plebaniak, R: Dynamic processes, fixed points, endpoints, asymmetric structures and investigations related to Caristi, Nadler and Banach in uniform spaces. Abstr. Appl. Anal. 2015, Article ID 942814 (2015)
Bakhtin, IA: The contraction principle in quasimetric spaces. In: Functional Analysis, vol. 30, pp. 26-37 (1989)
Czerwik, S: Nonlinear set-valued contraction mappings in b-metric spaces. Atti Semin. Mat. Fis. Univ. Modena 46, 263-276 (1998)
Shah, MH, Hussain, N: Nonlinear contractions in partially ordered quasi b-metric spaces. Commun. Korean Math. Soc. 27(1), 117-128 (2012)
Alghamdi, MA, Hussain, N, Salimi, P: Fixed point and coupled fixed point theorems on b-metric-like spaces. J. Inequal. Appl. 2013, 402 (2013)
Zhu, CX, Chen, CF, Zhang, X: Some results in quasi-b-metric-like spaces. J. Inequal. Appl. 2014, 437 (2014)
Zoto, K, Kumari, PS, Hoxha, E: Some fixed point theorems and cyclic contractions in dislocated and dislocated quasi-metric spaces. Am. J. Numer. Anal. 2(3), 79-84 (2014)
Acknowledgements
The authors would like to thank Science Achievement Scholarship of Thailand which provides funding for the research.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Klin-eam, C., Suanoom, C. Dislocated quasi-b-metric spaces and fixed point theorems for cyclic contractions. Fixed Point Theory Appl 2015, 74 (2015). https://doi.org/10.1186/s13663-015-0325-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13663-015-0325-2