A Pata-type fixed point theorem in modular spaces with application

Abstract

In this paper, we present a Pata-type fixed point theorem in modular spaces which generalizes and improves some old results. As an application, we study the existence of solutions of integral equations in modular function spaces.

MSC:47H10, 46A80, 45G10.

1 Introduction and preliminaries

In 1950 Nakano [1] introduced the theory of modular spaces in connection with the theory of ordered spaces. Musielak and Orlicz [2] in 1959 redefined and generalized it to obtain a generalization of the classical function spaces $L^p$. Khamsi et al. [3] investigated the fixed point results in modular function spaces. There exists an extensive literature on the topic of the fixed point theory in modular spaces (see, for instance, [4–14]) and the papers referenced there.

Recently, Pata [15] improved the Banach principle. Using the idea of Pata, we prove a fixed point theorem in modular spaces. Then we show how our results generalize old ones. Also, we prepare an application of our main results to the existence of solutions of integral equations in Musielak-Orlicz spaces.

In the first place, we recall some basic notions and facts about modular spaces.

Definition 1.1 Let X be an arbitrary vector space over K ($=\mathbb{R}$ or ℂ).

• (a) A function $\rho :X\to [0,+\mathrm{\infty }]$ is called a modular if for all $x,y\in X$.

  • (i) $\rho (x)=0$ if and only if $x=0$;

  • (ii) $\rho (\alpha x)=\rho (x)$ for every scalar α with $|\alpha |=1$;

  • (iii) $\rho (\alpha x+\beta y)\le \rho (x)+\rho (y)$ if $\alpha +\beta =1$ and $\alpha \ge 0$, $\beta \ge 0$

• (b) If (iii) is replaced by we say that ρ is convex modular.

  • (iv) $\rho (\alpha x+\beta y)\le \alpha \rho (x)+\beta \rho (y)$ if $\alpha +\beta =1$ and $\alpha \ge 0$, $\beta \ge 0$,

• (c) A modular ρ defines a corresponding modular space, i.e., the vector space $X_{\rho }$ given by

  $$X_{\rho }=\{x\in X:\rho (\lambda x)\to 0\text{ as }\lambda \to 0\}.$$

Example 1.2 Let $(X,\parallel \cdot \parallel )$ be a norm space, then $\parallel \cdot \parallel$ is a convex modular on X. But the converse is not true.

In general the modular ρ does not behave as a norm or a distance because it is not subadditive. But one can associate to a modular the F-norm (see [16]).

Definition 1.3 The modular space $X_{\rho }$ can be equipped with the F-norm defined by

$$|x{|}_{\rho }=inf\{\alpha >0;\rho \left(\frac{x}{\alpha }\right)\le \alpha \}.$$

Namely, if ρ is convex, then the functional

$${\parallel x\parallel }_{\rho }=inf\{\alpha >0;\rho \left(\frac{x}{\alpha }\right)\le 1\},$$

is a norm called the Luxemburg norm in $X_{\rho }$ which is equivalent to the F-norm $|\cdot {|}_{\rho }$.

Definition 1.4 Let $X_{\rho }$ be a modular space.

• (a) A sequence ${\{x_n\}}_{n\in \mathbb{N}}$ in $X_{\rho }$ is said to be:

  • (i) ρ-convergent to x if $\rho (x_n-x)\to 0$ as $n\to \mathrm{\infty }$.

  • (ii) ρ-Cauchy if $\rho (x_n-x_m)\to 0$ as $n,m\to \mathrm{\infty }$.

• (b) $X_{\rho }$ is ρ-complete if every ρ-Cauchy sequence is ρ-convergent.

• (c) A subset $B\subseteq X_{\rho }$ is said to be ρ-closed if ${\{x_n\}}_{n\in \mathbb{N}}\subset B$ with $x_n\to x$, then $x\in B$.

• (d) A subset $B\subseteq X_{\rho }$ is called ρ-bounded if

  $${\delta }_{\rho }(B)=sup\{\rho (x-y):x,y\in B\}<\mathrm{\infty },$$

where ${\delta }_{\rho }(B)$ is called the ρ-diameter of B.

• (e) We say that ρ has the Fatou property if

  $$\rho (x-y)\le lim\hspace{0.17em}inf\rho (x_n-y_n),$$

whenever $\rho (x_n-x)\to 0$, $\rho (y_n-y)\to 0$ as $n\to \mathrm{\infty }$.

• (f) ρ is said to satisfy the ${\mathrm{△}}_2$-condition if

  $$\rho (x_n)\to 0\Rightarrow \rho (2x_n)\to 0(\text{as }n\to \mathrm{\infty }).$$

It is easy to check that for every modular ρ and $x,y\in X_{\rho }$,

• (1) $\rho (\alpha x)\le \rho (\beta x)$ for each $\alpha ,\beta \in {\mathbb{R}}^{+}$ with $\alpha \le \beta$,

• (2) $\rho (x+y)\le \rho (2x)+\rho (2y)$.

Now we recall some basic concepts about modular function spaces as formulated by Kozlowski [17].

Let Ω be a nonempty set and let Σ be a nontrivial σ-algebra of subsets of Ω. Let 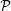be a δ-ring of subsets of Σ such that $E\cap A\in \mathcal{P}$ for any $E\in \mathcal{P}$ and $A\in \mathrm{\Sigma }$. Let us assume that there is an increasing sequence of sets $K_n\in \mathcal{P}$ such that $\mathrm{\Omega }=\bigcup K_n$.

In other words, the family 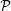plays the role of δ-ring of subsets of finite measure. By ℰ we denote the linear space of all simple functions with supports from .

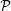By ℳ we denote the space of all measurable functions, i.e., all functions $f:\mathrm{\Omega }\to \mathbb{R}$ such that there exists a sequence $\{g_n\}\in \mathcal{E}$, $|g_n|\le |f|$ and $g_n(w)\to f(w)$ for all $w\in \mathrm{\Omega }$. By $1_A$ we denote the characteristic function of the set A.

Definition 1.5 A function $\rho :\mathcal{E}\times \mathrm{\Sigma }\to [0,+\mathrm{\infty }]$ is called a function modular if

• (i) $\rho (0,E)=0$ for any $E\in \mathrm{\Sigma }$;

• (ii) $\rho (f,E)\le \rho (g,E)$ whenever $|f(w)|\le |g(w)|$ for any $w\in \mathrm{\Omega }$, $f,g\in \mathcal{E}$ and $E\in \mathrm{\Sigma }$;

• (iii) $\rho (f,\cdot ):\mathrm{\Sigma }\to [0,+\mathrm{\infty }]$ is a σ-sub-additive measure for every $f\in \mathcal{E}$;

• (iv) $\rho (\alpha ,A)\to 0$ as α decreases to 0 for every $A\in \mathcal{P}$, where $\rho (\alpha ,A)=\rho (\alpha 1_A,A)$;

• (v) for any $\alpha >0$, $\rho (\alpha ,\cdot )$ is order continuous on 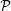, that is, $\rho (\alpha ,A_n)\to 0$ if $\{A_n\}\in \mathcal{P}$ and decreases to ϕ.

The definition of ρ is then extended to $f\in \mathcal{M}$ by

$$\rho (f,E)=sup\{\rho (g,E);g\in \mathcal{E},|g(w)|\le |f(w)|,w\in \mathrm{\Omega }\}.$$

For simplicity, we write $\rho (f)$ instead of $\rho (f,\mathrm{\Omega })$.

One can verify that the functional $\rho :\mathcal{M}\to [0,+\mathrm{\infty }]$ is a modular in the sense of Definition 1.1. The modular space determined by ρ will be called a modular function space and will be denoted by $L_{\rho }$. Recall that

$$L_{\rho }=\{f\in \mathcal{M}:\underset{\alpha \to 0}{lim}\rho (\alpha f)=0\}.$$

Example 1.6 (1) The Orlicz modular is defined for every measurable real function f by the formula

$$\rho (f)={\int }_{\mathbb{R}}\phi \left(|f(t)|\right)d\mu (t),$$

where μ denotes the Lebesgue measure in ℝ and $\phi :\mathbb{R}\to [0,\mathrm{\infty })$ is continuous. We also assume that $\phi (u)=0$ if and only if $u=0$ and $\phi (t)\to \mathrm{\infty }$ as $t\to \mathrm{\infty }$.

The modular space induced by the Orlicz modular, is a modular function space and is called the Orlicz space. (2) The Musielak-Orlicz modular spaces (see [2]).

Let

$$\rho (f)={\int }_{\mathrm{\Omega }}\phi (\omega ,|f(\omega )|)d\mu (\omega ),$$

where μ is a σ-finite measure on Ω and $\phi :\mathrm{\Omega }\times \mathbb{R}\to [0,\mathrm{\infty })$ satisfy the following:

• (i) $\phi (\omega ,u)$ is a continuous even function of u, which is non-decreasing for $u>0$, such that $\phi (\omega ,0)=0$, $\phi (\omega ,u)>0$ for $u\ne 0$ and $\phi (\omega ,u)\to \mathrm{\infty }$ as $u\to \mathrm{\infty }$;

• (ii) $\phi (\omega ,u)$ is a measurable function of ω for each $u\in \mathbb{R}$;

• (iii) $\phi (\omega ,u)$ is a convex function of u for each $\omega \in \mathrm{\Omega }$.

It is easy to check that ρ is a convex modular function and the corresponding modular space is called the Musielak-Orlicz space and is denoted by $L^{\phi }$.

In the following we give some notions which will be used in the next sections.

Definition 1.7 (Khamsi [18])

Let C be a subset of a modular function space $L_{\rho }$. A mapping $T:C\to C$ is called ρ-strict contraction if there exists $\lambda <1$ such that

$$\rho (Tf-Tg)\le \lambda \rho (f-g)$$

for all $f,g\in C$.

Theorem 1.8 (Khamsi [18])

Let C be a ρ-complete, ρ-bounded subset of $L_{\rho }$ and let $T:C\to C$ be a ρ-strict contraction. Then T has a unique fixed point $z\in C$. Moreover, z is the ρ-limit of the iterate of any point in C under the action of T.

Definition 1.9 (Taleb and Hanebaly [4])

The function $u:I\to L^{\phi }$, where $I=[0,A]$ for all $A>0$, is said to be continuous at $t_0\in I$ if for $t_n\in I$ and $t_n\to t_0$, then $\rho (u(t_n)-u(t))\to 0$ as $n\to \mathrm{\infty }$.

If we consider the Musielak-Orlicz modular with ${\mathrm{△}}_2$-condition, then the continuity of u at $t_0$ is equivalent to

$$(t_n\to t_0)\Rightarrow {\parallel u(t_n)-u(t_0)\parallel }_{\rho }\to 0(\text{as }n\to \mathrm{\infty }).$$

Let $C^{\phi }=C(I,L^{\phi })$ be the space of all continuous mappings from $I=[0,A]$ into $L^{\phi }$.

Proposition 1.10 (Taleb and Hanebaly [4])

Suppose that the Musielak-Orlicz modular ρ satisfies ${\mathrm{△}}_2$-condition and $B\subset L^{\phi }$ is a ρ-closed and convex subset of $L^{\phi }$. For $a\ge 0$, let ${\rho }_a(u)=sup\{e^{-at}\rho (u(t)):t\in I\}$ for $u\in C^{\phi }$, then

• (1) $(C^{\phi },{\rho }_a)$ is a modular space, and ${\rho }_a$ is a convex modular satisfying the Fatou property and the ${\mathrm{△}}_2$-condition;

• (2) $C^{\phi }$ is ${\rho }_a$-complete;

• (3) $C_0^{\phi }=C(I,B)$ is a ${\rho }_a$-closed, convex subset of $C^{\phi }$.

2 Main results

Let $X_{\rho }$ be a modular function space, C be a nonempty, ρ-complete and ρ-bounded subset of $X_{\rho }$, $x_0$ be an arbitrary point in C and let $\psi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ be an increasing function vanishing with continuity at zero. Also, consider the vanishing sequence depending on $\alpha \ge 1$, $w_n(\alpha )={(\frac{\alpha }{n})}^{\alpha }{\sum }_{k=1}^n\psi (\frac{\alpha }{k})$. Let $T:C\to C$ be a mapping. For notational purposes, we define $T^n(x)$, $x\in X_{\rho }$ and $n\in \{0,1,2,\dots \}$ inductively by $T^0(x)=x$ and $T^{n+1}(x)=T(T^n(x))$.

Theorem 2.1 Let $\alpha \ge 1$, $\beta >0$ and $k\ge 0$ be fixed constants. If the inequality

$$\rho (Tx-Ty)\le (1-ϵ)\rho (x-y)+{ϵ}^{\alpha }\psi (ϵ){(\rho (x-y)+k)}^{\beta }$$

(2.1)

is satisfied for every $ϵ\in [0,1]$ and every $x,y\in C$, then T has a unique fixed point $z=T(z)$ which is the $\rho \text{-}lim$ of the iterate of $x_0$ under the action of T.

Proof We first show existence. Let $ϵ=0$ in (2.1), thus we get

$$\rho (Tx-Ty)\le \rho (x-y)$$

(2.2)

for all $x,y\in C$. We construct a sequence ${\{x_n\}}_{n=0}^{\mathrm{\infty }}$ such that $x_n=T(x_{n-1})$ for all $n\in \mathbb{N}$. Now we claim $\{x_n\}$ is ρ-Cauchy sequence in C. By (2.1), (2.2) for all $m,n\in \mathbb{N}$, we have

$$\rho (x_{n+m}-x_n)\le (1-ϵ)\rho (x_{n+m-1}-x_{n-1})+{ϵ}^{\alpha }\psi (ϵ){(\rho (x_{n+m-1}-x_{n-1})+k)}^{\beta }.$$

(2.3)

Let $M:={({\delta }_{\rho }(C)+k)}^{\beta }$. Since C is ρ-bounded, M is finite and from (2.3) we have

$$\rho (x_{n+m+1}-x_{n+1})\le (1-ϵ)\rho (x_{n+m}-x_n)+{ϵ}^{\alpha }\psi (ϵ)M.$$

Letting $ϵ=1-{(\frac{n}{n+1})}^{\alpha }$, we have $ϵ\le \frac{\alpha }{n+1}$. Keeping in mind that ψ is an increasing function,

$$\begin{array}{c}\rho (x_{n+m+1}-x_{n+1})\le \frac{n^{\alpha }}{{(n+1)}^{\alpha }}\rho (x_{n+m}-x_n)+\frac{{\alpha }^{\alpha }}{{(n+1)}^{\alpha }}\psi \left(\frac{\alpha }{n+1}\right)M\hfill \\ \Rightarrow {(n+1)}^{\alpha }\rho (x_{n+m+1}-x_{n+1})\le n^{\alpha }\rho (x_{n+m}-x_n)+{\alpha }^{\alpha }\psi \left(\frac{\alpha }{n+1}\right)M.\hfill \end{array}$$

(2.4)

Letting $r_n:=n^{\alpha }\rho (x_{n+m}-x_n)$, we have from (2.4)

$$\begin{array}{rl}{r}_{n+1}& \le r_n+{\alpha }^{\alpha }\psi \left(\frac{\alpha }{n+1}\right)M\\ \le r_{n-1}+{\alpha }^{\alpha }\psi \left(\frac{\alpha }{n}\right)M+{\alpha }^{\alpha }\psi \left(\frac{\alpha }{n+1}\right)M\\ ⋮\\ \le r_0+{\alpha }^{\alpha }M\sum _{k=1}^{n+1}\psi \left(\frac{\alpha }{k}\right)\\ ={\alpha }^{\alpha }M\sum _{k=1}^{n+1}\psi \left(\frac{\alpha }{k}\right).\end{array}$$

Therefore

$$\rho (x_{n+m}-x_n)\le {\left(\frac{\alpha }{n}\right)}^{\alpha }M\sum _{k=1}^n\psi \left(\frac{\alpha }{k}\right)=M{w}_n(\alpha ).$$

(2.5)

Taking limit as $n\to \mathrm{\infty }$ from both sides of (2.5), we get $\rho (x_{n+m}-x_n)\to 0$ as $n\to \mathrm{\infty }$. Then $\{x_n\}$ is ρ-Cauchy sequence in C. Since C is ρ-complete, there exists $z\in C$ such that $\rho (x_n-z)\to 0$ as $n\to \mathrm{\infty }$. From (2.1) we get

$$\begin{array}{rl}\rho \left(\frac{Tz-z}{2}\right)& \le \rho (Tz-x_n)+\rho (x_n-z)\\ \le (1-ϵ)\rho (z-x_{n-1})+{ϵ}^{\alpha }\psi (ϵ){(\rho (z-x_{n-1})+k)}^{\beta }+\rho (x_n-z).\end{array}$$

Taking limit as $ϵ\to 0$ afterwards as $n\to \mathrm{\infty }$, we get

$$\rho \left(\frac{Tz-z}{2}\right)\le \rho (z-x_{n-1})+\rho (x_n-z)\to 0.$$

Then $Tz=z$. On the other hand, by (2.5), we have

$$\begin{array}{rl}\rho (z-T^n{x}_0)& =\rho (Tz-T^n{x}_0)=\rho (z-x_{n+1})\\ =\underset{m\to \mathrm{\infty }}{lim}\rho (x_{m+n+1}-x_{n+1})\\ \le M{w}_n(\alpha )\to 0(\text{as }n\to \mathrm{\infty }).\end{array}$$

Thus z is the $\rho \text{-}lim$ of the iterate of $x_0$ under the action of T.

To show uniqueness, we suppose that y is another fixed point of T. Then from (2.1) we have

$$\rho (z-y)=\rho (Tz-Ty)\le (1-ϵ)\rho (z-y)+{ϵ}^{\alpha }\psi (ϵ){(\rho (z-y)+k)}^{\beta }.$$

(2.6)

Then $\rho (z-y)\le {ϵ}^{\alpha -1}\psi (ϵ){(\rho (z-y)+k)}^{\beta }\to 0$ as $ϵ\to 0$, therefore $z=y$.

If for each $ϵ\in (0,1]$ strict inequality occurs in (2.6), then

$${ϵ}^{1-\alpha }\rho (z-y)<\psi (ϵ){(\rho (z-y)+k)}^{\beta }.$$

Taking limit as $ϵ\to 0$, we get contradiction unless $\rho (z-y)=0$. □

Remark 2.2 Theorem 2.1 is stronger than Theorem 1.8. Indeed, with the hypothesis of Theorem 1.8, if for each $f,g\in C$ and $\lambda \in (0,1)$, we have

$$\rho (Tf-Tg)\le \lambda \rho (f-g),$$

then by $\alpha =\beta =1$, $k=0$ and

$$\psi (ϵ)=\left(\frac{{\gamma }^{\gamma }}{{(1+\gamma )}^{1+\gamma }{(1-\lambda )}^{\gamma }}\right){ϵ}^{\gamma }$$

for arbitrary $\gamma >0$, we get

$$\rho (Tf-Tg)\le (1-ϵ)\rho (f-g)+ϵ\psi (ϵ)\rho (f-g)$$

is satisfied for every $ϵ\in [0,1]$. Thus from Theorem 2.1, T has a unique fixed point z which is the $\rho \text{-}lim$ of $T^n{f}_0$ for an arbitrary point $f_0$ in C.

3 Application

In this section, we study the existence of solution of the following integral equation:

$$u(t)=e^{-t}{f}_0+{\int }_0^t{e}^{s-t}Tu(s)ds,$$

(3.1)

where

(H₁) $T:B\to B$ is ρ-Lipschitz, i.e.,

$$\mathrm{\exists }\kappa >0,\rho (Tu-Tv)\le \kappa \rho (u-v)(u,v\in B);$$

(H₂) B is a ρ-closed, ρ-bounded, convex subset of the Musielak-Orlicz space $L^{\phi }$ satisfying the ${\mathrm{△}}_2$-condition;

(H₃) $f_0\in B$ is fixed.

Theorem 3.1 Under the conditions (H₁)-(H₃), for all $A>0$, integral equation (3.1) has a solution $u\in C^{\phi }=C([0,A],L^{\phi })$.

Proof Define the operator S on $C_0^{\phi }$ by

$$Su(t)=e^{-t}{f}_0+{\int }_0^t{e}^{s-t}Tu(s)ds$$

for all $t\in I:=[0,A]$.

1st step. First we show that $S:C_0^{\phi }\to C_0^{\phi }$. Let $u\in C_0^{\phi }$ and $t_n,t_0\in I$ for all $n\in \mathbb{N}$ with $t_n\to t_0$ as $n\to \mathrm{\infty }$. We know u is ρ-continuous thus $\rho (u(t_n)-u(t_0))\to 0$. From (H₁) we get $\rho (Tu(t_n)-Tu(t_0))\to 0$ as $n\to \mathrm{\infty }$, thus Tu is ρ-continuous at $t_0$. By ${\mathrm{△}}_2$-condition Tu is ${\parallel \cdot \parallel }_{\rho }$-continuous at $t_0$, therefore Su is ${\parallel \cdot \parallel }_{\rho }$-continuous at $t_0$ and consequently is ρ-continuous at $t_0$. Also, we have

$${\int }_0^t{e}^{s-t}Tu(s)ds\in \left({\int }_0^t{e}^{s-t}ds\right)\overline{\mathit{co}}\{Tu(s);0\le s\le t\}\subseteq (1-e^{-t})\overline{\mathit{co}}B,$$

where $\overline{\mathit{co}}B$ is a closed convex hull of B in $(L^{\phi },{\parallel \cdot \parallel }_{\rho })$.

But B is convex and ρ-closed, then $\overline{\mathit{co}}B=B\subseteq {\overline{B}}_{\rho }=B$, hence

$$Su(t)\in e^{-t}B+(1-e^{-t})B\subseteq B(\mathrm{\forall }t\in I).$$

2nd step. We show that $C_0^{\phi }$ is ${\rho }_a$-complete and ${\rho }_a$-bounded.

By Proposition 1.10, $C_0^{\phi }$ is a ${\rho }_a$-closed subset of ${\rho }_a$-complete space $C^{\phi }$, hence $C_0^{\phi }$ is ${\rho }_a$-complete too.

Now let $u,v\in C_0^{\phi }$. By 1st step $u(t),v(t)\in B$ for all $t\in I$, then

$${\rho }_a(u-v)=sup\{e^{-at}\rho (u(t)-v(t));t\in I\}\le {\delta }_{\rho }(B)<\mathrm{\infty },$$

therefore

$${\delta }_{{\rho }_a}\left(C_0^{\phi }\right)=sup\{{\rho }_a(u-v);u,v\in C_0^{\phi }\}<\mathrm{\infty }.$$

3rd step. For $u,v\in C_0^{\phi }$, we have

$${\rho }_a(Su-Sv)\le \kappa \left(\frac{1-e^{-(1+a)A}}{1+a}\right){\rho }_a(u-v).$$

(3.2)

Let $w\in C^{\phi }$ and $\{t_0,t_1,\dots ,t_n\}$ be any division of $[0,t]$.

Now suppose

$$sup\{|t_{i+1}-t_i|,i=0,1,\dots ,n-1\}\to 0$$

as $n\to \mathrm{\infty }$, then

$${\parallel \sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}w(t_i)-{\int }_0^t{e}^{s-t}w(s)ds\parallel }_{\rho }\to 0.$$

By ${\mathrm{△}}_2$-condition,

$$\rho (\sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}w(t_i)-{\int }_0^t{e}^{s-t}w(s)ds)\to 0.$$

Using the Fatou property, we get

$$\rho ({\int }_0^t{e}^{s-t}w(s)ds)\le lim\hspace{0.17em}inf\rho (\sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}w(t_i)).$$

(3.3)

Furthermore,

$$\sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}\le {\int }_0^t{e}^{s-t}ds\le 1-e^{-t}\le 1-e^{-A}<1.$$

By the convexity of ρ, we have

$$\begin{array}{rl}\rho (\sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}w(t_i))& \le \sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}\rho (w(t_i))\\ =\sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{t_i-t}{e}^{a{t}_i}{e}^{-a{t}_i}\rho (w(t_i))\\ \le \sum _{i=0}^{n-1}(t_{i+1}-t_i)e^{(1+a)t_i-t}{\rho }_a(w)\\ \le \left({\int }_0^t{e}^{(1+a)s-t}ds\right){\rho }_a(w).\end{array}$$

It follows from (3.3) that

$$\rho ({\int }_0^t{e}^{s-t}w(s)ds)\le \left(\frac{e^{at}-e^{-t}}{1+a}\right){\rho }_a(w).$$

(3.4)

On the other hand,

$$\rho (Su(t)-Sv(t))=\rho \left({\int }_0^t{e}^{s-t}(Tu(s)-Tv(s))\right)ds.$$

Thus by (3.4), we have

$$\rho (Su(t)-Sv(t))\le \left(\frac{e^{at}-e^{-t}}{1+a}\right){\rho }_a(Tu-Tv),$$

since T is ρ-Lipschitz, we have

$$\begin{array}{rl}\rho (Su(t)-Sv(t))& \le \left(\frac{e^{at}-e^{-t}}{1+a}\right)\underset{t\in I}{sup}{e}^{-at}\rho (Tu(t)-Tv(t))\\ \le \left(\frac{e^{at}-e^{-t}}{1+a}\right)\kappa \underset{t\in I}{sup}{e}^{-at}\rho (u(t)-v(t))\\ =\left(\frac{e^{at}-e^{-t}}{1+a}\right)\kappa {\rho }_a(u-v).\end{array}$$

Therefore

$$\begin{array}{rl}{e}^{-at}\rho (Su(t)-Sv(t))& \le \kappa \left(\frac{1-e^{-(1+a)t}}{1+a}\right){\rho }_a(u-v)\\ \le \kappa \left(\frac{1-e^{-(1+a)A}}{1+a}\right){\rho }_a(u-v)\end{array}$$

for all $t\in I$, which implies (3.2).

4th step. Let $\alpha =\beta =1$, $k=0$, $a>0$ with

$$e^{-(1+a)A}>\frac{\kappa -(1+a)}{\kappa }.$$

If we have

$$\frac{\kappa (1-e^{-(1+a)A})}{1+a}\le (1-ϵ)+{ϵ}^{1+\gamma }K$$

for all $\gamma >0$, $ϵ\in [0,1]$ and a constant K, then (3.2) implies that the inequality (2.1) is satisfied by $\psi (ϵ)=K{ϵ}^{\gamma }$. To this end, we define

$$F(ϵ)=(1-ϵ)+{ϵ}^{1+\gamma }K-\frac{\kappa (1-e^{-(1+a)A})}{1+a}.$$

Now imposing the conditions on F, which implies $0\le F(ϵ)$ for all $ϵ\in [0,1]$, we obtain

$$K=\frac{{\gamma }^{\gamma }{(1+a)}^{\gamma }}{{((1+a){(1+\gamma )}^{1+\frac{1}{\gamma }}-\kappa {(1+\gamma )}^{1+\frac{1}{\gamma }}(1-e^{-(1+a)A}))}^{\gamma }}.$$

Therefore, from steps 1 to 4 and Theorem 2.1, we conclude the existence of a fixed point of S which is the solution of integral equation (3.1). □