Abstract
This paper presents a framework of iterative methods for finding specific common fixed points of a nonexpansive self-mappings semigroup in a Banach space. We prove, with appropriate conditions, the strong convergence to the solution of some variational inequalities.
Similar content being viewed by others
1. Introduction
Let  be a nonempty closed convex subset of a Hilbert space
be a nonempty closed convex subset of a Hilbert space  , and let
, and let  be a nonlinear map. The classical variational inequality which is denoted by
be a nonlinear map. The classical variational inequality which is denoted by  is formulated as finding
is formulated as finding  such that
such that

for all  . We recall that
. We recall that  is called
is called  -strongly monotone, if for each
-strongly monotone, if for each  , we have
, we have

for a constant  , and also
, and also  -Lipschitzian if for each
-Lipschitzian if for each  , we have
, we have

for a constant  . Existence and uniqueness of solutions are important problems of the
. Existence and uniqueness of solutions are important problems of the  . It is known that if
. It is known that if  is a strongly monotone and Lipschitzian mapping on
is a strongly monotone and Lipschitzian mapping on  , then
, then  has a unique solution. An important problem is how to find a solution of
has a unique solution. An important problem is how to find a solution of  . It is known that
. It is known that

where  is an arbitrarily fixed constant and
is an arbitrarily fixed constant and  is the projection of
is the projection of  onto
onto  . This alternative equivalence has been used to study the existence theory of the solution and to develop several iterative type algorithms for solving variational inequalities. But the fixed point formulation in (1.4) involves the projection
. This alternative equivalence has been used to study the existence theory of the solution and to develop several iterative type algorithms for solving variational inequalities. But the fixed point formulation in (1.4) involves the projection  , which may not be easy to compute, due to the complexity of the convex set
, which may not be easy to compute, due to the complexity of the convex set  . So, projection methods and their variant forms can be implemented for solving variational inequalities.
. So, projection methods and their variant forms can be implemented for solving variational inequalities.
In order to reduce the complexity probably caused by the projection  , Yamada [1] (see also [2]) introduced a hybrid steepest-descent method for solving
, Yamada [1] (see also [2]) introduced a hybrid steepest-descent method for solving  . His idea is stated now. Assume that
. His idea is stated now. Assume that  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  . Recall that
. Recall that  is nonexpansive if
is nonexpansive if

Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian on
-Lipschitzian on  . Take a fixed number
. Take a fixed number  and a sequence
and a sequence  in
in  satisfying the following conditions:
satisfying the following conditions:
 ,
,
 ,
,
 .
.
Starting with an arbitrary initial guess  , generate a sequence
, generate a sequence  by the following algorithm:
by the following algorithm:

Yamada [1] proved that the sequence  converges strongly to a unique solution of
converges strongly to a unique solution of  . Xu and Kim [3] further considered and studied the hybrid steepest-descent algorithm (1.6). Their major contribution is that the strong convergence of (1.6) holds with condition
. Xu and Kim [3] further considered and studied the hybrid steepest-descent algorithm (1.6). Their major contribution is that the strong convergence of (1.6) holds with condition  being replaced by the following condition:
being replaced by the following condition:
 .
.
It is clear that condition  is strictly weaker than condition
is strictly weaker than condition  , coupled with conditions
, coupled with conditions  and
and  . Moreover,
. Moreover,  includes the important and natural choice
includes the important and natural choice  for
for  whereas
whereas  does not. For more related results, see [4, 5].
does not. For more related results, see [4, 5].
Let  be a Banach space we recall that a nonexpansive semigroup is a family
be a Banach space we recall that a nonexpansive semigroup is a family  of self-mappings of
of self-mappings of  satisfies the following conditions:
satisfies the following conditions:
(i) for
for  ,
,
(ii) for
for  and
and  ,
,
(iii) for
for  ,
,
-
(iv)
for each
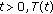 is nonexpansive. that is,
is nonexpansive. that is,

The problem is to find some fixed point in  . For this, so many algorithms have been developed and under some restrictions partial answers have been obtained [6–11].
. For this, so many algorithms have been developed and under some restrictions partial answers have been obtained [6–11].
Assume that  is a strongly monotone and Lipschitzian mapping and
is a strongly monotone and Lipschitzian mapping and  is a nonexpansive semigroup of self-mappings on
is a nonexpansive semigroup of self-mappings on  . For an appropriate
. For an appropriate  and starting from an arbitrary initial point
and starting from an arbitrary initial point  , we devise the following implicit, explicit, and modified iterations:
, we devise the following implicit, explicit, and modified iterations:



for  . With some appropriate assumptions, we prove the strong convergence of (1.8), (1.9), and (1.10) to the unique solution of the variational inequality
. With some appropriate assumptions, we prove the strong convergence of (1.8), (1.9), and (1.10) to the unique solution of the variational inequality  in
in  , where
, where  is the single-valued normalized duality mapping from
is the single-valued normalized duality mapping from  into
into  .
.
Our main purpose is to improve some of the conditions and results in the mentioned papers, especially those of Song and Xu [11].
2. Preliminaries
Let  be the unit sphere of the Banach space
be the unit sphere of the Banach space  . The space
. The space  is said to have Gateaux differentiable norm(or
is said to have Gateaux differentiable norm(or  is said to be smooth), if the limit
is said to be smooth), if the limit

exists for each  , and
, and  is said to have a uniformly Gateaux differentiable norm if for each
is said to have a uniformly Gateaux differentiable norm if for each  , the limit (2.1) converges uniformly for
, the limit (2.1) converges uniformly for  . Further,
. Further,  is said to be uniformly smooth if the limit (2.1) exists uniformly for
is said to be uniformly smooth if the limit (2.1) exists uniformly for  .
.
We denote  the normalized duality mapping from
the normalized duality mapping from  to
to  defined by
defined by

where  denotes the generalized duality pairing. It is well known if
denotes the generalized duality pairing. It is well known if  is smooth then any duality mapping on
is smooth then any duality mapping on  is single valued, and if
is single valued, and if  has a uniformly Gateaux differentiable norm, then the duality mapping is norm to weak* uniformly continuous on bounded sets.
has a uniformly Gateaux differentiable norm, then the duality mapping is norm to weak* uniformly continuous on bounded sets.
Recall that a Banach space  is said to be strictly convex if
is said to be strictly convex if  and
and  implies
implies  . In a strictly convex Banach space
. In a strictly convex Banach space  , we have that if
, we have that if  for
for  and
and  , then
, then  .
.
Now, we recall the concept of uniformly asymptotically regular semigroup. A continuous operator semigroup  on
on  is said to be uniformly asymptotically regular on
is said to be uniformly asymptotically regular on  if for all
if for all  and any bounded subset
and any bounded subset  of
of  , we have
, we have

The nonexpansive semigroup  is an example of uniformly asymptotically regular operator semigroup [11].
is an example of uniformly asymptotically regular operator semigroup [11].
Let  be a continuous linear functional on
be a continuous linear functional on  satisfying
satisfying  . Then, we know that
. Then, we know that  is a mean on
is a mean on  if and only if
if and only if

for every  . Sometimes, we use
. Sometimes, we use  instead of
instead of  . A mean
. A mean  on
on  is called a Banach limit if
is called a Banach limit if  . We know that if
. We know that if  is a Banach limit, then
is a Banach limit, then

for every  . Thus, if
. Thus, if  as
as  , then we have
, then we have

A discussion on these and related concepts can be found in [12].
We make use of the following well-known results throughout the paper.
Lemma 2.1 (see [12, Lemma 4.5.4]).
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  with a uniformly Gateaux differentiable norm, and let
with a uniformly Gateaux differentiable norm, and let  be a bounded sequence in
be a bounded sequence in  . If
. If  , then
, then

if and only if

for all  .
.
Lemma 2.2 (see [13]).
Let  ,
,  ,
,  , and let
, and let  be sequences such that
be sequences such that

for all  . Assume also that
. Assume also that  . Then, the following results hold:
. Then, the following results hold:
(i)if  (where
(where  ), then
), then  is bounded,
is bounded,
(ii)if we have

then  .
.
Lemma 2.3.
Let  be a real normed linear space, and let
be a real normed linear space, and let  be the normalized duality mapping on
be the normalized duality mapping on  . Then, for any
. Then, for any  , and
, and  , the following inequality holds:
, the following inequality holds:

In order to reduce any possible complexity in writing, we set  for a nonexpansive semigroup
for a nonexpansive semigroup  and
and

where  , for all
, for all  , and
, and  is a bounded sequence in
is a bounded sequence in  .
.
3. Implicit Iterative Method
Recall that if  is the single-valued normalized duality mapping from a Banach space
is the single-valued normalized duality mapping from a Banach space  into
into  , a nonlinear operator
, a nonlinear operator  is called
is called  -strongly monotone if for every
-strongly monotone if for every  , the following inequality holds:
, the following inequality holds:

for a constant  .
.
The following lemma will be be used to show the convergence of (1.8) and (1.9).
Lemma 3.1.
Let  be a Banach space, and let
be a Banach space, and let  be the single-valued normalized duality mapping from
be the single-valued normalized duality mapping from  into
into  . Assume also that
. Assume also that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian on
-Lipschitzian on  . Then,
. Then,

is a contraction on  for every
for every  .
.
Proof.
By using Lemma 2.3, we have

Thus, we obtain

and for  , we have
, we have  . That is,
. That is,  is a contraction, and the proof is complete.
is a contraction, and the proof is complete.
In the following theorem, which is the main result in this section, we establish the strong convergence of the sequence defined by (1.8).
Theorem 3.2.
Let  be a real Banach space with a uniformly Gateaux differentiable norm, and let
be a real Banach space with a uniformly Gateaux differentiable norm, and let  be a nonexpansive semigroup from
be a nonexpansive semigroup from  into itself. Let also
into itself. Let also  defined by (1.8) satisfies the following condition:
defined by (1.8) satisfies the following condition:

Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian. Assume also that
-Lipschitzian. Assume also that  is a sequence of positive numbers that
is a sequence of positive numbers that  and
and  . If
. If  , then
, then  converges strongly to some fixed point
converges strongly to some fixed point  , which is the unique solution in
, which is the unique solution in  to the variational inequality
to the variational inequality  , that is
, that is

Proof.
We divide the proof into several steps.
Step 1.
We first prove the uniqueness of the solution to  ; for this, we suppose
; for this, we suppose  are two solutions of
are two solutions of  . Thus, we have
. Thus, we have

By adding up the last two inequalities, we obtain

and so,  .
.
Step 2.
We claim that  is bounded. In fact, taking a fixed
is bounded. In fact, taking a fixed  , we have
, we have

Taking  and by using induction, we obtain
and by using induction, we obtain

therefore,  is bounded and so is
is bounded and so is  .
.
Step 3.
The sequence  is sequentially compact. To prove this, we assume that the set
is sequentially compact. To prove this, we assume that the set  contains some
contains some  such that
such that  for an arbitrary
for an arbitrary  . So, by using Lemma 2.1, we can obtain
. So, by using Lemma 2.1, we can obtain

On the other hand, for any  , we have
, we have

Thus,

Also, we have

It follows that

Combining (3.11) and (3.13) together, we get

This yields  . Hence, there exists a subsequence of
. Hence, there exists a subsequence of  such as
such as  that converges strongly to
that converges strongly to  ; that is,
; that is,  is sequentially compact.
is sequentially compact.
Step 4.
We claim that  is the solution of
is the solution of  . Since
. Since  is bounded, for any fixed point
is bounded, for any fixed point  , there exist a constant
, there exist a constant  such that
such that  . Therefore, we obtain
. Therefore, we obtain

Hence,

Note that the duality mapping  is single valued (
is single valued ( is smooth), and norm topology to weak* uniformly continuous on bounded sets of Banach space
is smooth), and norm topology to weak* uniformly continuous on bounded sets of Banach space  with uniformly Gateaux differentiable norm. Therefore,
with uniformly Gateaux differentiable norm. Therefore,

and by taking limit as  in two sides of (3.18), we obtain
in two sides of (3.18), we obtain

Cosequently,  is the unique solution of
is the unique solution of  .
.
Step 5.
 in norm. Indeed, we show that each cluster point of the sequence
in norm. Indeed, we show that each cluster point of the sequence  is equal to
is equal to  . Assume that
. Assume that  is another strong limit point of
is another strong limit point of  in
in  . Thanks to (3.15), we have the following two inequalities:
. Thanks to (3.15), we have the following two inequalities:

Therefore,

It yields that  , which proves the uniqness of
, which proves the uniqness of  . Thus,
. Thus,  itself converges strongly to
itself converges strongly to  . This completes the proof.
. This completes the proof.
4. Explicit Iterative Method
In this section, we will present our result of the strong convergence of (1.9), but first, we need to prove, with different approach, the following lemma.
Lemma 4.1.
Let  ,
,  ,
, ,
, ,
, ,μ, and
,μ, and  be as those in Theorem 3.2. If
be as those in Theorem 3.2. If  , and there exists a bounded sequence
, and there exists a bounded sequence  such that
such that

Then,

Proof.
By the uniqueness of  and with no loss of generality, we can choose
and with no loss of generality, we can choose  such that
such that

as  . Let
. Let  be the fixed point of the contraction
be the fixed point of the contraction

Then,

Now, by using Lemma 2.3, we have

Therefore,

Because  ,
,  and
and  are bounded, from (4.3) and (4.7), we conclude that
are bounded, from (4.3) and (4.7), we conclude that

Moreover, we have

By Theorem 3.2,  , as
, as  . So, using the boundedness of
. So, using the boundedness of  , we get
, we get

On the other hand, noticing that the sequence  is bounded and the duality mapping
is bounded and the duality mapping  is single-valued and norm to weak* uniformly continuous on bounded subsets of
is single-valued and norm to weak* uniformly continuous on bounded subsets of  , we conclude that
, we conclude that

Therefore, from (4.8) and (4.9), we obtain

This completes the proof.
Next, we prove the strong convergence of explicit iteration scheme (1.9).
Theorem 4.2.
Let  be a real Banach space with a uniformly Gateaux differentiable norm, and let
be a real Banach space with a uniformly Gateaux differentiable norm, and let  be a nonexpansive semigroup from
be a nonexpansive semigroup from  into itself. Let also
into itself. Let also  defined by (1.9) satisfies the following conditions:
defined by (1.9) satisfies the following conditions:
(i) ,
,
(ii) for all
for all  .
.
Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian, and that
-Lipschitzian, and that  is a sequence of positive numbers that
is a sequence of positive numbers that  . Assume also that the sequence
. Assume also that the sequence  in
in  satisfies the control condition
satisfies the control condition

If  , then
, then  converges strongly to some fixed point
converges strongly to some fixed point  , which is the unique solution in
, which is the unique solution in  for the following variational inequality:
for the following variational inequality:

Proof.
Existence and uniqueness of the solution of  is attained from Theorem 3.2. Now, we claim that
is attained from Theorem 3.2. Now, we claim that  is bounded. Indeed, taking a fixed
is bounded. Indeed, taking a fixed  , we have
, we have

Taking  ,
,  ,
,  , and using Lemma 2.2, we conclude that
, and using Lemma 2.2, we conclude that  is bounded and so is
is bounded and so is  .
.
Next, we prove that  converges strongly to the unique solution
converges strongly to the unique solution  of
of  . By definition of the algorithm and taking
. By definition of the algorithm and taking  , we have
, we have

Taking  ,
,  , and
, and  and using Lemma 4.1 together with Lemma 2.2 lead to
and using Lemma 4.1 together with Lemma 2.2 lead to  , that is,
, that is,  in norm. This completes the proof.
in norm. This completes the proof.
Corollary 4.3.
Let  be a real reflexive strictly convex Banach space with a uniformly Gateaux differentiable norm. Let also
be a real reflexive strictly convex Banach space with a uniformly Gateaux differentiable norm. Let also  be a nonexpansive semigroup from
be a nonexpansive semigroup from  into itself such that
into itself such that  . Assume that
. Assume that  defined by (1.9) satisfies condition
defined by (1.9) satisfies condition  in Theorem 4.2, then condition
in Theorem 4.2, then condition  holds.
holds.
Proof.
Clearly,  is a convex and continuous function. Because
is a convex and continuous function. Because  is a reflexive Banach space, according to [12, Theorem
is a reflexive Banach space, according to [12, Theorem  ],
],  is nonempty. Also, by convexity and continuity of
is nonempty. Also, by convexity and continuity of  , the set
, the set  is a closed convex subset of
is a closed convex subset of  . Since
. Since  for every
for every  and
and  , we have
, we have

So,  , and therefore
, and therefore  . Suppose that
. Suppose that  . Because every nonempty closed convex subset of a strictly convex and reflexive Banach space
. Because every nonempty closed convex subset of a strictly convex and reflexive Banach space  is a Chebyshev set, according to [14, Corollary
is a Chebyshev set, according to [14, Corollary  ], there exists a unique
], there exists a unique  such that
such that

On the other hand,  for all
for all  ,
,  and
and  is nonexpansive, so we get
is nonexpansive, so we get

that is,  , by uniqueness of
, by uniqueness of  . Thus,
. Thus,  . This completes the proof.
. This completes the proof.
Corollary 4.4.
Let  be a real Banach space, and let
be a real Banach space, and let  be a nonexpansive uniformly asymptotically regular semigroup from
be a nonexpansive uniformly asymptotically regular semigroup from  into itself. If
into itself. If  is defined by (1.9), where
is defined by (1.9), where  satisfies
satisfies  , then condition
, then condition  in Theorem 4.2 holds.
in Theorem 4.2 holds.
Proof.
From (1.9),  , and the boundedness of
, and the boundedness of  , we conclude that
, we conclude that

as  . On the other hand, the semigroup
. On the other hand, the semigroup  is uniformly asymptotically regular,
is uniformly asymptotically regular,  , and
, and  is a bounded subset in
is a bounded subset in  , so for all
, so for all  , we have
, we have

Hence,

So, from (4.20), (4.21), and (4.22), we get

and it completes the proof.
Remark 4.5.
According to Corollaries 4.3 and 4.4, our assumptions are weaker than those of Song and Xu [11]. Also, noticing that for a contraction  , the mapping
, the mapping  is strongly monotone and Lipschitzian. So, by replacing
is strongly monotone and Lipschitzian. So, by replacing  by
by  in (1.8) and (1.9), the following schemes are, respectively, obtained:
in (1.8) and (1.9), the following schemes are, respectively, obtained:

Remark 4.6.
In the same way and with the same conditions mentioned in Theorem 4.2, it's easy to see that the sequence  defined by
defined by

converges strongly to the variational inequality  .
.
5. Modified Iterative Method
In this section, we show that the modified sequence  defined by (1.10) also converges strongly to the solution of variational equality
defined by (1.10) also converges strongly to the solution of variational equality  , but first, we need to prove the following lemma.
, but first, we need to prove the following lemma.
Lemma 5.1.
Let  be a Banach space. Assume that
be a Banach space. Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian nonlinear operator and
-Lipschitzian nonlinear operator and  a nonexpansive mapping. If
a nonexpansive mapping. If  , where
, where  , then
, then

is a contraction on  .
.
Proof.
Considering the inequality

from Lemma 2.3 in a Banach space  , where
, where  is the normalized single-valued duality, we have
is the normalized single-valued duality, we have

Noticing that

we obtain

Thus, we have

Note that for  , we conclude
, we conclude  . That is,
. That is,  is a contraction and the proof is complete.
is a contraction and the proof is complete.
Theorem 5.2.
Let  be a real Banach space with a uniformly Gateaux differentiable norm and
be a real Banach space with a uniformly Gateaux differentiable norm and  a nonexpansive semigroup from
a nonexpansive semigroup from  into itself. Let also
into itself. Let also  defined by (1.10) satisfies the following conditions:
defined by (1.10) satisfies the following conditions:
(i) ,
,
(ii) for all
for all  .
.
Assume that  is
is  -strongly monotone and
-strongly monotone and  -Lipschitzian and
-Lipschitzian and  a sequence of positive numbers that
a sequence of positive numbers that  . Assume also that the sequences
. Assume also that the sequences  , where
, where  , and
, and  in
in  satisfy the following control conditions:
satisfy the following control conditions:
 ,
,
 does not take 0 as it's limit point.
does not take 0 as it's limit point.
Then,  converges strongly to some fixed point
converges strongly to some fixed point  , which is the unique solution in
, which is the unique solution in  for the variational inequality
for the variational inequality  .
.
Proof.
Existence and uniqueness of the solution of  is obtained from Theorem 3.2. We claim that
is obtained from Theorem 3.2. We claim that  is bounded. Indeed, taking a fixed
is bounded. Indeed, taking a fixed  , we have
, we have

Noticing that

and by assumption that there exists  so that
so that  , for all
, for all  . Thus, we get
. Thus, we get

and from Lemma 2.2, we conclude that  is bounded.
is bounded.
By Theorem 3.2, there exists a unique solution  to
to  . We prove that
. We prove that  converges strongly to
converges strongly to 

Taking  ,
,  , and
, and  and using Lemma 4.1 together with Lemma 2.2 imply
and using Lemma 4.1 together with Lemma 2.2 imply  , that is,
, that is,

This completes the proof.
Remark 5.3.
In Theorem 5.2, if  , then
, then  , and therefore we can remove
, and therefore we can remove  , also
, also  turns to
turns to  .
.
Remark 5.4.
We can easily see that under some restrictions all the strongly monotone and Lipschitzian nonlinear operators used in this paper are replaceable by strongly accretive and strictly pseudocontractive ones (see [15]).
References
Yamada I: The hybrid steepest-descent method for the variational inequality problem of the intersection of fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithm for Feasibility and Optimization. Edited by: Butnariu D, Censor Y, Reich S. Elsevier, New York, NY, USA; 2001:473–504.
Deutsch F, Yamada I: Minimizing certain convex functions over the intersection of the fixed point sets of nonexpansive mappings. Numerical Functional Analysis and Optimization 1998,19(1–2):33–56.
Xu HK, Kim TH: Convergence of hybrid steepest-descent methods for variational inequalities. Journal of Optimization Theory and Applications 2003,119(1):185–201.
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002,66(1):240–256. 10.1112/S0024610702003332
Saeidi S: Modified hybrid steepest-descent methods for variational inequalities and fixed points. Mathematical and Computer Modelling 2010,52(1–2):134–142. 10.1016/j.mcm.2010.01.023
Shioji N, Takahashi W: Strong convergence of approximated sequences for nonexpansive mappings in Banach spaces. Proceedings of the American Mathematical Society 1997,125(12):3641–3645. 10.1090/S0002-9939-97-04033-1
Shioji N, Takahashi W: Strong convergence theorems for asymptotically nonexpansive semigroups in Hilbert spaces. Nonlinear Analysis: Theory, Methods and Applications 1998,34(1):87–99. 10.1016/S0362-546X(97)00682-2
Suzuki T: On strong convergence to common fixed points of nonexpansive semigroups in Hilbert spaces. Proceedings of the American Mathematical Society 2003,131(7):2133–2136. 10.1090/S0002-9939-02-06844-2
Xu H-K: A strong convergence theorem for contraction semigroups in Banach spaces. Bulletin of the Australian Mathematical Society 2005,72(3):371–379. 10.1017/S000497270003519X
Chen R, Song Y: Convergence to common fixed point of nonexpansive semigroups. Journal of Computational and Applied Mathematics 2007,200(2):566–575. 10.1016/j.cam.2006.01.009
Song Y, Xu S: Strong convergence theorems for nonexpansive semigroup in Banach spaces. Journal of Mathematical Analysis and Applications 2008,338(1):152–161. 10.1016/j.jmaa.2007.05.021
Takahashi W: Nonlinear Functional Analysis: Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2002.
Maingé P-E: Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,325(1):469–479. 10.1016/j.jmaa.2005.12.066
Megginson RE: An Introduction to Banach Space Theory, Graduate Texts in Mathematics. Volume 183. Springer, New York, NY, USA; 1998:xx+596.
Ceng L-C, Ansari QH, Yao J-C: Mann-type steepest-descent and modified hybrid steepest-descent methods for variational inequalities in Banach spaces. Numerical Functional Analysis and Optimization 2008,29(9–10):987–1033. 10.1080/01630560802418391
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1155/2011/187439.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mohamadi, I. Iterative Methods for Variational Inequalities over the Intersection of the Fixed Points Set of a Nonexpansive Semigroup in Banach Spaces. Fixed Point Theory Appl 2011, 620284 (2011). https://doi.org/10.1155/2011/620284
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/620284



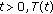 is nonexpansive. that is,
is nonexpansive. that is,