1. Introduction

Random matrix theory, since its inception, has been known as a powerful tool for solving practical problems arising in physics, statistics, and engineering [1–3]. Recently, an important aspect of random matrix theory, that is, the distribution of the eigenvalues of random matrices, has been successfully applied to the analysis and design of wireless communication systems [4]. These applications, mostly concerning the multiple-input multiple-output (MIMO) systems, can be summarized as follows. In single-user MIMO systems, the eigenvalue distributions of Wishart matrices (a Wishart matrix [1] is formed by multiplying a Gaussian random matrix (of the size ) with its Hermitian transposition (given that ). If , the product matrix was termed the pseudo-Wishart matrix [5]) were widely applied to the analysis of MIMO channel capacity [6–11] and specific MIMO techniques, such as MIMO maximum ratio combining (MIMO MRC) (MIMO MRC is a technique that transmits signals along the strongest eigen-direction of the channel. It was also known as maximum-ratio transmission [12], transmit-receive diversity [13], and MIMO beamforming [14]) [15–17] and, MIMO singular value decomposition (MIMO SVD) (MIMO SVD, also known as MIMO multichannel beamforming [18], and spatial multiplexing MIMO [19, 20], is a generalization of MIMO MRC. It transmits multiple data streams along several strongest eigen-directions of the channel). [18–21], given that the MIMO channel was Rayleigh/Rician faded. For channels that are not Rayleigh/Rician faded (e.g., the double-scattering [22] fading channel to be discussed in Section 4), the eigenvalue distributions of Wishart matrices also played an essential role in the performance analysis of MIMO systems [23–30]. Even for relay channels, statistical distributions of the eigenvalues were shown very useful in the derivation of the channel capacity [31, 32]. In multiuser MIMO systems, the eigenvalue distribution of a random matrix (characterized by the channel matrix of the desired user and that of the interferers) was applied to the performance analysis of MIMO optimum combing (MIMO OC) [33–41]. Furthermore, in cognitive radio networks, the eigenvalue distributions of random matrices were recently applied to devise effective algorithms for spectrum sensing [42–44].

Given its importance in various applications, the eigenvalue distribution of random matrices is arguably one of the hottest topic in communication engineering. During the past two years, general methods for obtaining these eigenvalue distributions were developed, applying for a general class of random matrices. To be specific, Ordóñez et al. [20] presented a general expression for the marginal distributions of the ordered eigenvalues, while Zanella et al. [45, 46] proposed alternative expressions for the same distributions. The results, however, need separate expressions to cover the Wishart and pseudo-Wishart matrices. This problem was later avoided in the new expression of Chiani and Zanella [21], which was given in terms of the "determinant" of the rank- tensor. After that, a simpler expression for the eigenvalue distribution was presented by Sun et al. [41], where only conventional (-dimensional) determinants were involved.

In this paper, we aim at finding a new expression for the eigenvalue distribution, which is even simpler than Sun's result. To that end, we first show that many important random matrices, especially those in the summary above, share a common structure on the joint distributions of their (nonzero) eigenvalues. Based on the common structure, we then derive the marginal distributions of the ordered eigenvalues, using a classical result from the theory of order statistics, along with the multilinear property of the determinant. It turns out that the new expression we obtained is compacter in representation and more efficient in computational complexity, when comparing with existing results. The new result can unify the eigenvalue distributions of Wishart and pseudo-Wishart matrices with only a single expression. Moreover, it is given in conventional (-dimensional) determinants, and importantly, it replaces many functions in Sun's result with constant numbers, greatly improving the computational efficiency. As an illustrative application of the new expression, we analyze the performance of MIMO SVD systems, assuming the (uncorrelated) double-scattering [22] fading channels. It is worth noting that, different from the Rayleigh/Rician fading channels, where the performance of MIMO SVD were well-studied in [18], the behaviors of MIMO SVD in double-scattering channels is still not clear (expect for some primary results in [47] by the authors). In this context, we derive first the joint eigenvalue distribution of the MIMO channel matrix, using the law of total probability. Then, based on the joint distribution, we apply the general result to get the marginal distribution for each ordered eigenvalue. After that, we analyze the performance of the MIMO SVD. Analytical expressions for the average SER and the outage probability of the system are derived and validated (with numerical simulations). As the simulation results illustrate, the analytical expressions agree perfectly with the Monte Carlo results.

The rest of this paper is organized as follows. Section 2 presents the common structure of the joint eigenvalue distributions. Based on the common structure, Section 3 derives the general expression for the marginal eigenvalue distributions. Then, in Section 4, we analyze the performance of the MIMO SVD in double-scattering channels, by applying the general result. Finally, we summarize the paper in Section 5. Next, we list the notations used throughout this paper: all vectors and matrices are represented with bold symbols; denotes the transposition of a matrix; denotes the Hermitian transposition of a matrix; denotes an matrix with only zero elements; denotes the identity matrix; denotes that is an complex matrix; is the th element of a matrix ; denotes the determinant of a matrix; is the determinant of a matrix whose th element is ; is the expectation of a random variable with respect to ; denotes that is an complex Gaussian matrix with a mean value , a row correlation , and a column correlation .

2. Joint Distributions of Ordered Eigenvalues

In this section, we show that the random matrices discussed in Section 1 share a common structure on the joint probability density functions (PDFs) of their eigenvalues. (Although the common structure can be found in various random matrices (Rayleigh, Rician, and double-scattering, etc.), it is not true that all random matrices have this structure on the joint PDF of their eigenvalues. A good example in this point is the Nakagami-Hoyt channel, whose joint eigenvalue PDF of the channel matrix is different from (1), see [48, Equation ()], for more details. It is also worth noting that, for non-Gaussian random matrices, obtaining exact expressions on their joint eigenvalue distributions is generally difficult. Very few results can be found in the literature. In this paper, we focus on exact eigenvalue distributions, and thus, we consider mainly Gaussian and Gaussian-related random matrices.) Indeed, this common structure (formulated as the proposition below) was previously reported in [20, 45, 49] among others.

Proposition 1.

Let denote a Hermitian random matrix discussed in Section 1, and let , , denote the nonzero ordered eigenvalues of  . Then, the joint PDF of can be expressed as

(1)

where , is the joint PDF of , is a constant coefficient, is a generic function, and are and matrices (), respectively, whose elements are given by

(2)

with being an arbitrary constant, 's and 's being a generic function.

Next, we verify the proposition above with random matrices discussed in Section 1. (Let and denote two mutually independent complex Gaussian matrices).

() Single-user MIMO systems:

()(uncorrelated) Rayleigh fading channels: Let with , then the joint PDF of the eigenvalues of the Wishart matrix is [6]

(3)

where , , and

(4)

Clearly, the joint PDF above is in the form of (1). For semicorrelated Rayleigh and uncorrelated Rician fading channels, one can also verify that the joint PDFs are in the same form as (1), see [18, 20, 45, 46].

()Double-scattering channels: Let , and , with , , and being three natural numbers, then the nonzero ordered eigenvalues of are jointly distributed as

(5)

where , , and

(6)
(7)

and the matrices and are defined by

(8)

with being the modified Bessel function of the second kind [50, Equation ()].

Proof.

See Appendix A.

Again, the joint distribution fits well in the from of Proposition 1. More results pertaining to double-scattering channels can be found in [47, Lemma ].

() Multiuser MIMO systems:

()OC without thermal noise: Let with , with , and has positive and descendingly ordered eigenvalues , then the eigenvalues of are jointly distributed as [38]

(9)

where , , and

(10)

with being the generalized hypergeometric function [50, Equation ()].

Obviously, the joint PDF here also belongs to the class defined by Proposition 1. For more examples, see [40, 51].

()OC with thermal noise: Let , with the matrix having positive eigenvalues in descendent order , then the joint PDF of the nonzero eigenvalues of   is [41]

(11)

where , , and

(12)

with being the upper incomplete Gamma function [50, Equation ()].

Again, the joint PDF has the same form as (1). More results can be found in [39].

In summary, the random matrices discussed in Section 1 share a common structure on the joint distributions of their eigenvalues. Based on this common structure, we derive in the following section a general result for the marginal distribution of each ordered eigenvalue.

3. Marginal Distributions of Ordered Eigenvalues

3.1. General Expression for the Marginal Distribution

Theorem 1.

If the joint PDF of the ordered eigenvalues is given by (1), the marginal CDF of the th largest eigenvalue can be expressed as ()

(13)

where , is a permutation of that satisfies and . The second summation is over all permutations, that is, in total.

Proof.

See Appendix B.

Given the marginal CDF, the corresponding marginal PDF is easy to obtain, given the well-known result on the derivative of a determinant [52, Equation ()],

(14)

where is an matrix with each element being a function of , and is identical to , except that all elements in the th column are replaced by their derivatives with respect to .

In the literature, exact expressions on the marginal distributions of the ordered eigenvalues were reported in [20, 45, 46]. (The expression obtained in [45, 46] was given in the form of a sum of terms. That form allows closed-form evaluation of moments and characteristic functions of the eigenvalues.) These results, however, needed separate expressions to represent the eigenvalue distributions of Wishart (i.e., ) and pseudo-Wishart (i.e., ) matrices. In contrast, Theorem 1 unifies the two cases ( and ) with only a single expression. It is also worth noting that, although another unified expression could be found in [21], the result there was given in terms of the determinant of rank- tensor . (Letting be a rank- tensor, that is, for , the "determinant" of , denoted by , is given by [7]  where and are permutations of the integers , the summation is over all possible permutations, and is the sign of the permutation.) which was computationally complex, especially comparing to our new result in a conventional (-dimensional) determinant form. Perhaps the most related work in the literature is [41]. To see the difference between [41] and Theorem 1 above, we rewrite [41, Lemma ] in the following proposition. After comparing the two results, one can clearly see that our expression is much more efficient in computational complexity, since the functions in (15) are replaced by constant numbers in (13).

Proposition 2.

The marginal CDF of can be alteratively expressed as

(15)

Proof.

By the definition of marginal CDF, we have

(16)
(17)

where . Substituting (1) into (17) and invoking the generalized Cauchy-Binet formula [41, Lemma ] the multi-nested integration can be carried out analytically. As such, we get the desired result.

It is also worth noting that the work of this paper can be viewed as an interesting proof for the equivalence between (13) and (15), because both Theorem 1 and Proposition 2 represent the same eigenvalue distribution.

3.2. Specific Eigenvalue Distributions

As a simple application of the general result, we particularize into the eigenvalue distribution of the double-scattering channel matrix.

Corollary 1.

Given that the ordered eigenvalues of () are jointly distributed as (5), the marginal CDF of the th largest eigenvalue can be expressed as

(18)

where is given in (7), the second summation is over all combinations of and with being a permutation of , and

(19)

with

(20)

Proof.

Define

(21)

The integral above can be written in a closed form by invoking [50, Equations () and ()]. The results are given in (20). Substituting (5) into (13) and using (21) completes the proof.

The marginal CDF of the largest eigenvalue (i.e., ) of the double-scattering channel matrix was reported earlier in [14]. The expression above extends this result to marginal distributions of all ordered eigenvalues. We also note that marginal CDFs of the ordered eigenvalues were also investigated in the authors' previous work [47]. However, the result there were derived based on Proposition 2 above.

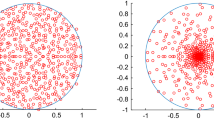
In Figure 1, we plot the eigenvalue CDFs of the matrix (), when , , and . The analytical results are computed by (18), and the Monte Carlo results are based on channel realizations. A perfect agreement is observed between the analytical and Monte Carlo curves.

Figure 1
figure 1

Marginal CDFs of ordered eigenvalues of when , , and .

Full size image

4. Performance Analysis of MIMO SVD Systems

In this section, we consider performance analysis of MIMO SVD systems. Uncorrelated double-scattering fading channels are assumed, where the MIMO channel matrix is modeled as [14] (the double-scattering channel considered here was also termed the Rayleigh-product channel [14])

(22)

where , , , , and are the numbers of transmit antennas, receive antennas, and the scatterers, respectively. The matrix represents the fading channel between the transmitter and the scatterers, while represents the channel between the scatterers and the receiver. The introduction of the double-scattering model is due to the fact that [53] MIMO channels exhibits a rank deficient behavior when there is not enough scattering around the transmitter and receiver (a typical example is the keyhole/pinhole channel [54], where the MIMO channel matrix has rank one regardless of the number of transmit and receive antennas, since only one scatterer exists in the environment). In this model, the MIMO channel matrix is characterized by the product (concatenation) of two Gaussian matrices, representing the channel from the transmitter to the scatterers, and the channel from the scatterers to the receiver, respectively. Varying the number of the scatterers, the double-scattering model describes a broad family of practical channels, ranging from conventional Rayleigh channel (infinite scatterers) to degenerate keyhole channel (only one scatterer). In the rest of this section, we use notations , , , and as they were defined in (6).

4.1. System Model

Consider a MIMO channel with transmit and receive antennas. The received vector can be expressed as

(23)

where is the channel matrix, is the vector of signals transmitted, and is the complex additive white Gaussian noise (AWGN) vector with zero mean and identity covariance matrix. In MIMO SVD, assuming perfect channel state information (CSI) at the transmitter, the transmit vector is formed by mapping () modulated symbols () onto transmit antennas via a linear precoding:

(24)

where is the spatial pre-coding matrix. Here, the columns of are the right singular vectors of corresponding to the largest singular values. Under the assumption of perfect CSI at the receiver, the decision statistics of MIMO SVD, denoted by (), is obtained by weighting the receive signal with a spatial equalizing matrix

(25)

where the columns of are the left singular vectors of corresponding to the largest singular values. After such pre-coding and equalization, the MIMO channel is decomposed into a set of equivalent single-input single-output (SISO) channels, whose input-output relation is

(26)

where is the th largest eigenvalue of , and is the complex AWGN with zero mean and unit variance (i.e., variance per complex dimension). Hereafter, we term these SISO channels as the sub-channels of MIMO SVD. Letting denote the power allocated to the th subchannel, the instantaneous SNR of the th subchannel can be expressed as ()

(27)

Clearly, the performance of MIMO SVD depends directly on the eigenvalues s.

It is worth noting that, although the capacity-achievable power allocation for MIMO SVD is water-filling [6], exact analysis of such allocation strategy is very difficult (in water-filling, each allocated power is a function of all eigenvalues , leading to an intractable SER expression of each subchannel [18], Ft. 1). For this reason, earlier researches on MIMO SVD generally considered fixed (but not necessarily uniform) power allocation [18, 20]. (Indeed, given a sufficiently high SNR, the water-filling power strategy tends to a uniform power allocation, that is, a special case of the fixed allocation [20].) Following this direction, we consider here fixed power allocation, but it worth noting hat the results obtained can serve as a starting point for the analysis of channel-dependent power allocations [19], as well as the analysis of diversity-multiplexing tradeoff [55].

4.2. Performance Analysis

First of all, we consider the outage performance of MIMO SVD. The outage probability, as an important measure of service quality, is defined by the probability that the received SNR drops below an acceptable threshold . For convenience sake, we assume equal power allocation is employed, that is, with denoting the total transmit power (normalized by the noise variance). As such, the SNRs of the subchannels are ordered as , and the outage probability of the overall system is dominated by the worst subchannel (corresponding to ). The exact expression on outage probability is then obtained by substituting the CDF (18) into the equation below

(28)
(29)

Next, we consider the SER of MIMO SVD. Given the average SER of many general modulation formats (BPSK, BFSK, -PAM, etc.) [56] ((30) also provides good approximations to the SERs of other modulation formats, such as -PSK [56, Equation ()])

(30)

where is the instantaneous SNR, is the Gaussian -function, and are modulation-specific constants (e.g., , for BPSK), the average SER of the th subchannel of the MIMO SVD system can be expressed as (after some algebraic manipulations)

(31)

Substituting (18) into (31) yields the analytical expression for the average SER. Although deriving a closed-form result for (31) seems difficult, the expression above can be evaluated numerically, which is more efficient than running Monte Carlo simulations. Since independent signals are sent over different subchannels, the global SER (i.e., the average SER of the overall system) can be obtained by averaging the SERs of the active subchannels [18, 19]

(32)

4.3. Numerical Examples

In this subsection, numerical simulations are used to verify the theoretical results above. For notational convenience, we denote the double-scattering channel with transmit antennas, receive antennas, and scatterers by a three-tuple . We also assume that all subchannels are active (i.e., ), upon which equal power allocation is employed (i.e., for all ).

In Figure 2, we fix the SNR threshold at  dB to evaluate the impact of scatterer insufficiency on the outage probability of MIMO SVD. Three channel configurations are considered: , , and . Results from standard Rayleigh channel (i.e., ) is also provided for the purpose of comparison. The analytical results are computed with (29), and each Monte Carlo result is based on channel realizations. From the figure, we observe an exact agreement between the analytical and Monte Carlo curves. Also, we observe that the lack of scattering certainly degrade the performance of the system, which is consistent with our intuition.

Figure 2
figure 2

Comparisons on outage probabilities of MIMO SVD in different channels: , , , and .

Full size image

In Figure 3, we plot the SERs of the MIMO SVD subchannels in a double-scattering channel, using uncoded BPSK modulation. It is shown that all analytical results agree with the Monte-Carlo curves perfectly. It is also observed that the first and second strongest subchannels outperform the third subchannel significantly. This indicates that further improvements (in SER) is possible if only a subset of subchannels is used. In-depth analysis along this direction can be found in [57] on the linear transceiver design with adaptive number of sub-streams, and also in [55] on the fundamental tradeoff between diversity and multiplexing of MIMO SVD (note that both papers assumed conventional Rayleigh/Rican fading).

Figure 3
figure 3

Subchannel SER of MIMO SVD in a double-scattering channel when uncoded BPSK is used.

Full size image

5. Conclusion

The eigenvalue distribution of random matrices has long been known as a powerful tool for analyzing and designing communication systems. In this paper, we derived a new expression for the marginal distributions of the ordered eigenvalues of certain important random matrices. The new expression was compacter in representation and more efficient in computational complexity, when comparing to existing results in the literature. As an illustrative application, we then used the general result to analyze the performance of MIMO SVD systems, under the assumption of double-scattering fading channels. Joint and marginal eigenvalue distributions of the channel matrix were presented, which further yielded analytical expressions on the average SER and outage probability of the system. Finally, the theoretical results were verified with numerical simulations.