Abstract
We present a new generating function related to the  -Bernoulli numbers and
-Bernoulli numbers and  -Bernoulli polynomials. We give a new construction of these numbers and polynomials related to the second-kind Stirling numbers and
-Bernoulli polynomials. We give a new construction of these numbers and polynomials related to the second-kind Stirling numbers and  -Bernstein polynomials. We also consider the generalized
-Bernstein polynomials. We also consider the generalized  -Bernoulli polynomials attached to Dirichlet's character
-Bernoulli polynomials attached to Dirichlet's character  and have their generating function . We obtain distribution relations for the
and have their generating function . We obtain distribution relations for the  -Bernoulli polynomials and have some identities involving
-Bernoulli polynomials and have some identities involving  -Bernoulli numbers and polynomials related to the second kind Stirling numbers and
-Bernoulli numbers and polynomials related to the second kind Stirling numbers and  -Bernstein polynomials. Finally, we derive the
-Bernstein polynomials. Finally, we derive the  -extensions of zeta functions from the Mellin transformation of this generating function which interpolates the
-extensions of zeta functions from the Mellin transformation of this generating function which interpolates the  -Bernoulli polynomials at negative integers and is associated with
-Bernoulli polynomials at negative integers and is associated with  -Bernstein polynomials.
-Bernstein polynomials.
Similar content being viewed by others
1. Introduction, Definitions, and Notations
Let  be the complex number field. We assume that
be the complex number field. We assume that  with
with  and that the
and that the  -number is defined by
-number is defined by  in this paper.
in this paper.
Many mathematicians have studied  -Bernoulli,
-Bernoulli,  -Euler polynomials, and related topics (see [1–23]). It is known that the Bernoulli polynomials are defined by
-Euler polynomials, and related topics (see [1–23]). It is known that the Bernoulli polynomials are defined by

and that  are called the
are called the  th Bernoulli numbers.
th Bernoulli numbers.
The recurrence formula for the classical Bernoulli numbers  is as follows,
is as follows,

(see [1, 3, 23]). The  -extension of the following recurrence formula for the Bernoulli numbers is
-extension of the following recurrence formula for the Bernoulli numbers is

with the usual convention of replacing  by
by  (see [5, 7, 14]).
(see [5, 7, 14]).
Now, by introducing the following well-known identities

(see [6]).
The generating functions of the second kind Stirling numbers and  -Bernstein polynomials, respectively, can be defined as follows,
-Bernstein polynomials, respectively, can be defined as follows,


Throughout this paper,  ,
,  ,
,  ,
,  , and
, and  will respectively denote the ring of rational integers, the field of rational numbers, the ring
will respectively denote the ring of rational integers, the field of rational numbers, the ring  -adic rational integers, the field of
-adic rational integers, the field of  -adic rational numbers, and the completion of the algebraic closure of
-adic rational numbers, and the completion of the algebraic closure of  . Let
. Let  be the normalized exponential valuation of
be the normalized exponential valuation of  such that
such that  . If
. If  , we normally assume
, we normally assume  or
or  so that
so that  for
for  (see [7–19]).
(see [7–19]).
In this study, we present a new generating function related to the  -Bernoulli numbers and
-Bernoulli numbers and  -Bernoulli polynomials and give a new construction of these numbers and polynomials related to the second kind Stirling numbers and
-Bernoulli polynomials and give a new construction of these numbers and polynomials related to the second kind Stirling numbers and  -Bernstein polynomials. We also consider the generalized
-Bernstein polynomials. We also consider the generalized  -Bernoulli polynomials attached to Dirichlet's character
-Bernoulli polynomials attached to Dirichlet's character  and have their generating function. We obtain distribution relations for the
and have their generating function. We obtain distribution relations for the  -Bernoulli polynomials and have some identities involving
-Bernoulli polynomials and have some identities involving  -Bernoulli numbers and polynomials related to the second kind Stirling numbers and
-Bernoulli numbers and polynomials related to the second kind Stirling numbers and  -Bernstein polynomials. Finally, we derive the
-Bernstein polynomials. Finally, we derive the  -extensions of zeta functions from the Mellin transformation of this generating function which interpolates the
-extensions of zeta functions from the Mellin transformation of this generating function which interpolates the  -Bernoulli polynomials at negative integers and are associated with
-Bernoulli polynomials at negative integers and are associated with  -Bernstein polynomials.
-Bernstein polynomials.
2. New Approach to 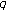 -Bernoulli Numbers and Polynomials
-Bernoulli Numbers and Polynomials
Let  be the set of natural numbers and
be the set of natural numbers and  . For
. For  with
with  , let us define the
, let us define the  -Bernoulli polynomials
-Bernoulli polynomials  as follows,
as follows,

Note that

where  are classical Bernoulli polynomials. In the special case
are classical Bernoulli polynomials. In the special case  ,
,  are called the
are called the  th
th  -Bernoulli numbers. That is,
-Bernoulli numbers. That is,

From (2.1) and (2.3), we note that

From (2.1) and (2.3), we can easily derive the following equation:

Equations (2.4) and (2.5), we see that  and
and

Therefore, we obtain the following theorem.
Theorem 2.1.
For  , one has
, one has

with the usual convention of replacing  and
and  .
.
From (2.1), one notes that

Therefore, one obtains the following theorem.
Theorem 2.2.
For  , one has
, one has

By (2.1), one sees that

By (2.1) and (2.10), one obtains the following theorem.
Theorem 2.3.
For  , one has
, one has

From (2.11) one can derive that, for  ,
,

By (2.12), one sees that, for  ,
,

Therefore, one obtains the following theorem.
Theorem 2.4.
For  , one has
, one has

In (2.9), substitute  instead of
instead of  , one obtains
, one obtains

which is the relation between  -Bernoulli polynomials,
-Bernoulli polynomials,  -Bernoulli numbers, and
-Bernoulli numbers, and  -Bernstein polynomials. In (1.5), substitute
-Bernstein polynomials. In (1.5), substitute  instead of
instead of  , one gets
, one gets

In (2.16), substitute  instead of
instead of  , and putting the result in (2.15), one has the following theorem.
, and putting the result in (2.15), one has the following theorem.
Theorem 2.5.
For  and
and  , one has
, one has

where  and
and  are the second kind Stirling numbers and
are the second kind Stirling numbers and  -Bernstein polynomials, respectively.
-Bernstein polynomials, respectively.
Let  be Dirichlet's character with
be Dirichlet's character with  . Then, one defines the generalized
. Then, one defines the generalized  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  as follows,
as follows,

In the special case  ,
,  are called the
are called the  th generalized
th generalized  -Bernoulli numbers attached to
-Bernoulli numbers attached to  . Thus, the generating function of the generalized
. Thus, the generating function of the generalized  -Bernoulli numbers attached to
-Bernoulli numbers attached to  are as follows,
are as follows,

By (2.1) and (2.18), one sees that

Therefore, one obtains the following theorem.
Theorem 2.6.
For  and
and  , one has
, one has

By (2.18) and (2.19), one sees that

Hence,

For  , one now considers the Mellin transformation for the generating function of
, one now considers the Mellin transformation for the generating function of  . That is,
. That is,

for  , and
, and  .
.
From (2.24), one defines the zeta type function as follows,

Note that  is an analytic function in the whole complex
is an analytic function in the whole complex  -plane. Using the Laurent series and the Cauchy residue theorem, one has
-plane. Using the Laurent series and the Cauchy residue theorem, one has

By the same method, one can also obtain the following equations:

For  ,one defines Dirichlet type
,one defines Dirichlet type  -
- -function as
-function as

where  . Note that
. Note that  is also a holomorphic function in the whole complex
is also a holomorphic function in the whole complex  -plane. From the Laurent series and the Cauchy residue theorem, one can also derive the following equation:
-plane. From the Laurent series and the Cauchy residue theorem, one can also derive the following equation:

In (2.23), substitute  instead of
instead of  , one obtains
, one obtains

which is the relation between the  th generalized
th generalized  -Bernoulli numbers and
-Bernoulli numbers and  -Bernoulli polynomials attached to
-Bernoulli polynomials attached to  and
and  -Bernstein polynomials. From (2.16), one has the following theorem.
-Bernstein polynomials. From (2.16), one has the following theorem.
Theorem 2.7.
For  and
and  , one has
, one has

One now defines particular  -zeta function as follows,
-zeta function as follows,

From (2.32), one has

where  is given by (2.25). By (2.26), one has
is given by (2.25). By (2.26), one has

Therefore, one obtains the following theorem.
Theorem 2.8.
For  , we have
, we have

References
Açıkgöz M, Aracı S: The relations between Bernoulli, Bernstein and Euler polynomials. Proceedings of the 8th International Conference of Numerical Analysis and Applied Mathematics (ICNAAM '10), March 2010, Rhodes, Greece, AIP
Açıkgöz M, Şimşek Y:A new generating function of
 -Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.
-Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.Açıkgöz M, Şimşek Y: On multiple interpolation functions of the Norlund-type Euler polynomials. Abstract Applied Analysis 2009, 2009:-14.
Açıkgöz M, Aracı S: On the generating function of Bernstein polynomials. Proceedings of the 8th International Conference of Numerical Analysis and Applied Mathematics (ICNAAM '10), March 2010, Rhodes, Greece, AIP
Carlitz L:
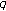 -Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987-1000. 10.1215/S0012-7094-48-01588-9
-Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987-1000. 10.1215/S0012-7094-48-01588-9Kac V, Cheung P: Quantum Calculus, Universitext. Springer, New York, NY, USA; 2001:x+112.
Kim T:A new approach to
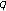 -zeta function. Advanced Studies in Contemporary Mathematics 2005,11(2):157-162.
-zeta function. Advanced Studies in Contemporary Mathematics 2005,11(2):157-162.Kim T:
 -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.Kim T:On
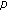 -adic
-adic 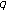 -
-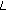 -functions and sums of powers. Discrete Mathematics 2002,252(1–3):179-187. 10.1016/S0012-365X(01)00293-X
-functions and sums of powers. Discrete Mathematics 2002,252(1–3):179-187. 10.1016/S0012-365X(01)00293-XKim T:
 -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.Kim T:Non-Archimedean
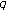 -integrals associated with multiple Changhee
-integrals associated with multiple Changhee  -Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.
-Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.Kim T:Power series and asymptotic series associated with the
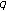 -analog of the two-variable
-analog of the two-variable  -adic
-adic 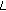 -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.Kim T:On the
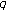 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037Kim T, Choi J, Kim Y-H:
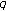 -Bernstein polynomials associated with
-Bernstein polynomials associated with 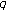 -Stirling numbers and Carlitz's
-Stirling numbers and Carlitz's 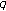 -Bernoulli numbers. Abstract and Applied Analysis (in press)
-Bernoulli numbers. Abstract and Applied Analysis (in press)Kim T, Jang L-C, Yi H:A note on the modified
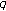 -Bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.
-Bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.Kim T:
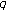 -Bernstein polynomials,
-Bernstein polynomials, 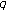 -Stirling numbers and
-Stirling numbers and 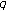 -Bernoulli polynomials. http://arxiv.org/abs/1008.4547
-Bernoulli polynomials. http://arxiv.org/abs/1008.4547Kim T, Jang L-C, Kim Y, Choi J:On p-adic analogue of
 -Bernstein polynomials and related integrals. Discrete Dynamics in Nature and Society 2010, 2010:-9.
-Bernstein polynomials and related integrals. Discrete Dynamics in Nature and Society 2010, 2010:-9.Kim T, Choi J, Kim Y-H:Some identities on the
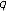 -Bernstein polynomials,
-Bernstein polynomials,  -Stirling numbers and
-Stirling numbers and  -Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010, 20: 335-341.
-Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010, 20: 335-341.Kim T:Analytic continuation of multiple
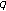 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.Kim T:Note on the Euler
 -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007Kim T:Barnes-type multiple
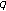 -zeta functions and
-zeta functions and 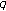 -Euler polynomials. Journal of Physics A 2010,43(25):-11.
-Euler polynomials. Journal of Physics A 2010,43(25):-11.Kim T, Rim S-H, Son J-W, Jang L-C:On the values of
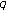 -analogue of zeta and
-analogue of zeta and 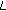 -functions. I. Algebra Colloquium 2002,9(2):233-240.
-functions. I. Algebra Colloquium 2002,9(2):233-240.Rademacher H: Topics in Analytic Number Theory. Springer, New York, NY, USA; 1973:ix+320.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Açikgöz, M., Erdal, D. & Araci, S. A New Approach to 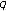 -Bernoulli Numbers and
-Bernoulli Numbers and  -Bernoulli Polynomials Related to
-Bernoulli Polynomials Related to 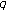 -Bernstein Polynomials.
Adv Differ Equ 2010, 951764 (2011). https://doi.org/10.1155/2010/951764
-Bernstein Polynomials.
Adv Differ Equ 2010, 951764 (2011). https://doi.org/10.1155/2010/951764
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/951764



 (see [
(see [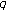 -Bernoulli Numbers and Polynomials
-Bernoulli Numbers and Polynomials -Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.
-Bernstein-type polynomials and their interpolation function. Abstract and Applied Analysis 2010, 2010:-12.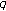 -Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987-1000. 10.1215/S0012-7094-48-01588-9
-Bernoulli numbers and polynomials. Duke Mathematical Journal 1948, 15: 987-1000. 10.1215/S0012-7094-48-01588-9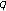 -zeta function. Advanced Studies in Contemporary Mathematics 2005,11(2):157-162.
-zeta function. Advanced Studies in Contemporary Mathematics 2005,11(2):157-162. -Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.
-Volkenborn integration. Russian Journal of Mathematical Physics 2002,9(3):288-299.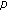 -adic
-adic 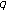 -
-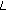 -functions and sums of powers. Discrete Mathematics 2002,252(1–3):179-187. 10.1016/S0012-365X(01)00293-X
-functions and sums of powers. Discrete Mathematics 2002,252(1–3):179-187. 10.1016/S0012-365X(01)00293-X -Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.
-Bernoulli numbers and polynomials associated with Gaussian binomial coefficients. Russian Journal of Mathematical Physics 2008,15(1):51-57.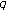 -integrals associated with multiple Changhee
-integrals associated with multiple Changhee  -Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.
-Bernoulli polynomials. Russian Journal of Mathematical Physics 2003,10(1):91-98.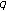 -analog of the two-variable
-analog of the two-variable  -adic
-adic 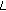 -function. Russian Journal of Mathematical Physics 2005,12(2):186-196.
-function. Russian Journal of Mathematical Physics 2005,12(2):186-196.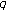 -extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037
-extension of Euler and Genocchi numbers. Journal of Mathematical Analysis and Applications 2007,326(2):1458-1465. 10.1016/j.jmaa.2006.03.037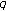 -Bernstein polynomials associated with
-Bernstein polynomials associated with 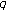 -Stirling numbers and Carlitz's
-Stirling numbers and Carlitz's 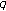 -Bernoulli numbers. Abstract and Applied Analysis (in press)
-Bernoulli numbers. Abstract and Applied Analysis (in press) -Bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12.
-Bernstein polynomials. Discrete Dynamics in Nature and Society 2010, 2010:-12. -Bernstein polynomials,
-Bernstein polynomials, 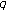 -Stirling numbers and
-Stirling numbers and 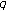 -Bernoulli polynomials.
-Bernoulli polynomials.  -Bernstein polynomials and related integrals. Discrete Dynamics in Nature and Society 2010, 2010:-9.
-Bernstein polynomials and related integrals. Discrete Dynamics in Nature and Society 2010, 2010:-9.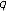 -Bernstein polynomials,
-Bernstein polynomials,  -Stirling numbers and
-Stirling numbers and  -Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010, 20: 335-341.
-Bernoulli numbers. Advanced Studies in Contemporary Mathematics 2010, 20: 335-341.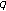 -zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76.
-zeta functions and their values at negative integers. Russian Journal of Mathematical Physics 2004,11(1):71-76. -zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007
-zeta functions. Journal of Number Theory 2009,129(7):1798-1804. 10.1016/j.jnt.2008.10.007 -zeta functions and
-zeta functions and  -Euler polynomials. Journal of Physics A 2010,43(25):-11.
-Euler polynomials. Journal of Physics A 2010,43(25):-11. -analogue of zeta and
-analogue of zeta and  -functions. I. Algebra Colloquium 2002,9(2):233-240.
-functions. I. Algebra Colloquium 2002,9(2):233-240.