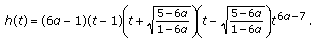Abstract
For  , the generalized logarithmic mean
, the generalized logarithmic mean  , arithmetic mean
, arithmetic mean  , and geometric mean
, and geometric mean  of two positive numbers
of two positive numbers  and
and  are defined by
are defined by  , for
, for  ,
,  , for
, for  ,
,  , and
, and  ,
,  , for
, for  , and
, and  ,
,  , for
, for  , and
, and  ,
,  , and
, and  , respectively. In this paper, we find the greatest value
, respectively. In this paper, we find the greatest value  (or least value
(or least value  , resp.) such that the inequality
, resp.) such that the inequality  (or
(or  , resp.) holds for
, resp.) holds for  (or
(or  , resp.) and all
, resp.) and all  with
with  .
.
Similar content being viewed by others
1. Introduction
For  , the generalized logarithmic mean
, the generalized logarithmic mean  and power mean
and power mean  with parameter
with parameter  of two positive numbers
of two positive numbers  and
and  are defined by
are defined by

and

respectively. It is well known that both means are continuous and increasing with respect to  for fixed
for fixed  and
and  . Recently, both means have been the subject of intensive research. In particular, many remarkable inequalities involving
. Recently, both means have been the subject of intensive research. In particular, many remarkable inequalities involving  and
and  can be found in the literature [1–9]. Let
can be found in the literature [1–9]. Let


, and  be the arithmetic, identric, logarithmic, geometric, and harmonic means of two positive numbers
be the arithmetic, identric, logarithmic, geometric, and harmonic means of two positive numbers  and
and  , respectively. Then
, respectively. Then

for all  .
.
In [10], Carlson proved that

for all  with
with  .
.
The following inequality is due to Sándor [11, 12]:

In [13], Lin established the following results: (1)  implies that
implies that  for all
for all  with
with  ; (2)
; (2)  implies that
implies that  for all
for all  with
with  ; (3)
; (3)  implies that there exist
implies that there exist  such that
such that  ; (4)
; (4)  implies that there exist
implies that there exist  such that
such that  . Hence the question was answered: what are the least value
. Hence the question was answered: what are the least value  and the greatest value
and the greatest value  such that the inequality
such that the inequality  holds for all
holds for all  with
with  .
.
Pittenger [14] established that

for all  , where
, where

Here,  and
and  are sharp and inequality (1.7) becomes equality if and only if
are sharp and inequality (1.7) becomes equality if and only if  or
or  or
or  . The case
. The case  reduces to Lin's results [13]. Other generalizations of Lin's results were given by Imoru [15].
reduces to Lin's results [13]. Other generalizations of Lin's results were given by Imoru [15].
Recently, some monotonicity results of the ratio between generalized logarithmic means were established in [16–18].
The aim of this paper is to prove the following Theorem 1.1.
Theorem 1.1.
Let  and
and  with
with  , then
, then
(1) for
for  ;
;
(2) for
for  , and
, and  for
for  , moreover, in each case, the bound
, moreover, in each case, the bound  for the sum
for the sum  is optimal.
is optimal.
2. Proof of Theorem 1.1
In order to prove our Theorem 1.1 we need a lemma, which we present in this section.
Lemma 2.1.
For  and
and  one has
one has
(1)If  , then
, then  for
for  ;
;
(2)If  , then
, then  for
for  ,
,  for
for  , and
, and  for
for  .
.
Proof.
-
(1)
If
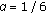 , then we clearly see that
, then we clearly see that 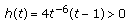 (2.1)
(2.1)
for  .
.
If  , then
, then

for  .
.
Therefore, Lemma 2.1( ) follows from (2.1) and (2.2).
) follows from (2.1) and (2.2).
-
(2)
If
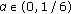 , then
, then 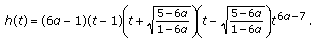 (2.3)
(2.3)
Therefore, Lemma 2.1(2) follows from (2.3).
Proof of Theorem 1.1.
Proof.
( ) If
) If  , then (1.1) leads to
, then (1.1) leads to

( ) We divide the proof into two cases.
) We divide the proof into two cases.
Case 1.

or  . From inequalities (1.5) and (1.6) we clearly see that
. From inequalities (1.5) and (1.6) we clearly see that

for  , and
, and

for  .
.
Case 2.

. Without loss of generality, we assume that  . Let
. Let  , then (1.1) leads to
, then (1.1) leads to

Let  , then simple computations yield
, then simple computations yield


where

Note that








where  is defined as in Lemma 2.1.
is defined as in Lemma 2.1.
We divide the proof into five subcases.
Subcase 2 A.

. From (2.18) and Lemma 2.1( ) we clearly see that
) we clearly see that  for
for  and
and  for
for  , then we know that
, then we know that  is strictly decreasing in
is strictly decreasing in  and strictly increasing in
and strictly increasing in  . Now from the monotonicity of
. Now from the monotonicity of  and (2.17) together with the fact that
and (2.17) together with the fact that  we clearly see that
we clearly see that  for
for  , then from (2.7)–(2.15) and
, then from (2.7)–(2.15) and  for
for  we get
we get  for
for  .
.
Subcase 2 B.

. Then (2.18) and Lemma 2.1(1) lead to

for  .
.
From (2.7)–(2.17) and (2.19) together with the fact that  for
for  we know that
we know that  for
for  .
.
Subcase 2 C.

. Then (2.18) and Lemma 2.1(1) imply that

for  .
.
From (2.7)–(2.17), (2.20) and  for
for  we know that
we know that  for
for  .
.
Subcase 2 D.

. Then (2.19) again yields, and  for
for  follows from (2.7)–(2.17) and (2.19) together with
follows from (2.7)–(2.17) and (2.19) together with  .
.
Subcase 2 E.

. Then (2.20) is also true, and  for
for  follows from (2.7)–(2.17), (2.20) and the fact that
follows from (2.7)–(2.17), (2.20) and the fact that  .
.
Next, we prove that the bound  for the sum
for the sum  is optimal in each case. The proof is divided into six cases.
is optimal in each case. The proof is divided into six cases.
Case 1.

. For any  and
and  , then (1.1) leads to
, then (1.1) leads to

where 
Let  making use of Taylor expansion, one has
making use of Taylor expansion, one has

Equations (2.21) and (2.22) imply that for any  , there exists
, there exists  , such that
, such that  for any
for any  and
and  .
.
Case 2.

. For any  and
and  , from (1.1) we have
, from (1.1) we have

where 
Let  making use of Taylor expansion, one has
making use of Taylor expansion, one has

Equations (2.23) and (2.24) imply that for any  , there exists
, there exists  , such that
, such that  for
for  and
and  .
.
Case 3.

. For  and
and  , we get
, we get

where 
Let  making use of Taylor expansion, one has
making use of Taylor expansion, one has

Equations (2.25) and (2.26) imply that for any  and any
and any  , there exists
, there exists  , such that
, such that  for
for  .
.
Case 4.

. For any  and
and  , we get
, we get

where 
Let  using Taylor expansion we have
using Taylor expansion we have

Equations (2.27) and (2.28) show that for any  and any
and any  , there exists
, there exists  , such that
, such that  for
for  .
.
Case 5.

. For any  and
and  , we have
, we have

where 
Let  making use of Taylor expansion we get
making use of Taylor expansion we get

Equations (2.29) and (2.30) imply that for any  and any
and any  , there exists
, there exists  , such that
, such that  for
for  .
.
Case 6.

. For any  and
and  , we get
, we get

where 
Let  , using Taylor expansion we have
, using Taylor expansion we have

From (2.31) and (2.32) we know that for any  and any
and any  , there exists
, there exists  , such that
, such that  for
for  .
.
At last, we propose two open problems as follows.
Open Problem 1
What is the least value  such that the inequality
such that the inequality

holds for  and all
and all  with
with  ?
?
Open Problem 2
What is the greatest value  such that the inequality
such that the inequality

holds for  and all
and all  with
with  ?
?
References
Alzer H: Ungleichungen für Mittelwerte. Archiv der Mathematik 1986, 47(5):422–426. 10.1007/BF01189983
Alzer H, Qiu S-L: Inequalities for means in two variables. Archiv der Mathematik 2003, 80(2):201–215. 10.1007/s00013-003-0456-2
Burk F: The geometric, logarithmic and arithmetic mean inequality. The American Mathematical Monthly 1987, 94(6):527–528. 10.2307/2322844
Janous W: A note on generalized Heronian means. Mathematical Inequalities & Applications 2001, 4(3):369–375.
Leach EB, Sholander MC: Extended mean values. II. Journal of Mathematical Analysis and Applications 1983, 92(1):207–223. 10.1016/0022-247X(83)90280-9
Sándor J: On certain inequalities for means. Journal of Mathematical Analysis and Applications 1995, 189(2):602–606. 10.1006/jmaa.1995.1038
Sándor J: On certain inequalities for means. II. Journal of Mathematical Analysis and Applications 1996, 199(2):629–635. 10.1006/jmaa.1996.0165
Sándor J: On certain inequalities for means. III. Archiv der Mathematik 2001, 76(1):34–40. 10.1007/s000130050539
Shi M-Y, Chu Y-M, Jiang Y-P: Optimal inequalities among various means of two arguments. Abstract and Applied Analysis 2009, 2009:-10.
Carlson BC: The logarithmic mean. The American Mathematical Monthly 1972, 79: 615–618. 10.2307/2317088
Sándor J: On the identric and logarithmic means. Aequationes Mathematicae 1990, 40(2–3):261–270.
Sándor J: A note on some inequalities for means. Archiv der Mathematik 1991, 56(5):471–473. 10.1007/BF01200091
Lin TP: The power mean and the logarithmic mean. The American Mathematical Monthly 1974, 81: 879–883. 10.2307/2319447
Pittenger AO: Inequalities between arithmetic and logarithmic means. Publikacije Elektrotehničkog Fakulteta. Serija Matematika i Fizika 1981, (678–715):15–18.
Imoru CO: The power mean and the logarithmic mean. International Journal of Mathematics and Mathematical Sciences 1982, 5(2):337–343. 10.1155/S0161171282000313
Chen Ch-P: The monotonicity of the ratio between generalized logarithmic means. Journal of Mathematical Analysis and Applications 2008, 345(1):86–89. 10.1016/j.jmaa.2008.03.071
Li X, Chen Ch-P, Qi F: Monotonicity result for generalized logarithmic means. Tamkang Journal of Mathematics 2007, 38(2):177–181.
Qi F, Chen Sh-X, Chen Ch-P: Monotonicity of ratio between the generalized logarithmic means. Mathematical Inequalities & Applications 2007, 10(3):559–564.
Acknowledgments
The authors wish to thank the anonymous referee for their very careful reading of the manuscript and fruitful comments and suggestions. This research is partly supported by N S Foundation of China under Grant 60850005, and N S Foundation of Zhejiang Province under Grants D7080080 and Y607128.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Long, BY., Chu, YM. Optimal Inequalities for Generalized Logarithmic, Arithmetic, and Geometric Means. J Inequal Appl 2010, 806825 (2010). https://doi.org/10.1155/2010/806825
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/806825



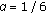 , then we clearly see that
, then we clearly see that 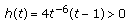
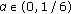 , then
, then