Abstract
The authors consider the multilinear Riesz potential operator defined by  , where
, where  denotes the
denotes the  -tuple
-tuple  ,
,  the nonnegative integers with
the nonnegative integers with  ,
,  ,
,  and
and  is a nonnegative
is a nonnegative  -dimensional Borel measure. In this paper, the boundedness for the operator
-dimensional Borel measure. In this paper, the boundedness for the operator  on the product of homogeneous Morrey-Herz spaces in nonhomogeneous setting is found.
on the product of homogeneous Morrey-Herz spaces in nonhomogeneous setting is found.
Similar content being viewed by others
1. Introduction
Let  denote a ball centered at
denote a ball centered at  with radius
with radius  , and for any
, and for any  ,
,  will mean the ball with the same center as
will mean the ball with the same center as  and with radius
and with radius  . A Borel measure
. A Borel measure  on
on  is called a doubling measure if it satisfies the so-called doubling condition; that is, there exists a constant
is called a doubling measure if it satisfies the so-called doubling condition; that is, there exists a constant  such that
such that

for every ball  . The doubling condition is a key feature for a homogeneous (metric) measure space. Many classical theories in Fourier analysis have been generalized to the homogeneous setting without too much difficulties. In the last decade, however, some researchers found that many results are still true without the assumption of the doubling condition on
. The doubling condition is a key feature for a homogeneous (metric) measure space. Many classical theories in Fourier analysis have been generalized to the homogeneous setting without too much difficulties. In the last decade, however, some researchers found that many results are still true without the assumption of the doubling condition on  (see, e.g., [1–4]). This fact has encouraged other researchers to study various theories in the nonhomogeneous setting. By a nonhomogeneous space we mean a (metric) measure space, here we will consider only
(see, e.g., [1–4]). This fact has encouraged other researchers to study various theories in the nonhomogeneous setting. By a nonhomogeneous space we mean a (metric) measure space, here we will consider only  , equipped with a nonnegative
, equipped with a nonnegative  -dimensional Borel measure
-dimensional Borel measure  , that is, a measure satisfying the growth condition
, that is, a measure satisfying the growth condition

for any ball  and
and  is a fixed real number such that
is a fixed real number such that  . Unless otherwise stated, throughout this paper we will always work in the nonhomogeneous setting.
. Unless otherwise stated, throughout this paper we will always work in the nonhomogeneous setting.
As one of the most important operators in harmonic analysis and its applications, the Riesz potential operator  defined by
defined by

was studied by García-Cuerva and Martell [1] in 2001. García-Cuerva and Martell proved that  is bounded from
is bounded from  to
to  for all
for all  and
and  and that
and that  is bounded from
is bounded from  to
to  . Here
. Here  and
and  denote the Lebesgue spaces and weak Lebesgue spaces with measure
denote the Lebesgue spaces and weak Lebesgue spaces with measure  , respectively.
, respectively.
Simultaneously many classical multilinear operators on Euclidean spaces with Lebesgue measure have been generalized for nondoubling measures, that is, the case nonhomogeneous setting see [3, 4]. For example, based on the work of Kenig and Stein [5], Lian and Wu [4] studied multilinear Riesz potential operator

in the nonhomogeneous case, where, and throughout this paper, we denote by  the
the  -tuple
-tuple  ,
,  the nonnegative integers with
the nonnegative integers with  . They obtained the following.
. They obtained the following.
Proposition 1.1 (see [4]).
Let  ,
,  with
with  ,
,  , then
, then
(a)if each  ,
,  is bounded from
is bounded from  to
to  ,
,
(b)if  for some
for some  ,
,  is bounded from
is bounded from  to
to  .
.
Obviously, it is Lemma 7 in [5] if  is the Lebesgue measure in the proposition above and it is a multilinear setting of the result of García-Cuerva and Martell [1].
is the Lebesgue measure in the proposition above and it is a multilinear setting of the result of García-Cuerva and Martell [1].
In addition, in the article [6–8], we have obtained the boundedness of the operator  on the product of Morrey type spaces, (weak) homogeneous Morrey-Herz spaces, and Herz type Hardy spaces in the classical case and extended the result of Kenig and Stein. As a continuation of previous work in [4, 6–8], in this paper, we will study the operator
on the product of Morrey type spaces, (weak) homogeneous Morrey-Herz spaces, and Herz type Hardy spaces in the classical case and extended the result of Kenig and Stein. As a continuation of previous work in [4, 6–8], in this paper, we will study the operator  in the product of (weak) homogeneous Morrey-Herz spaces in the nonhomogeneous setting.
in the product of (weak) homogeneous Morrey-Herz spaces in the nonhomogeneous setting.
The definitions of the (weak) homogeneous Morrey-Herz spaces  and (weak) homogeneous Herz spaces
and (weak) homogeneous Herz spaces  will be given in Section 2, here we only point out that
will be given in Section 2, here we only point out that  and
and  for
for  .
.
We will establish the following boundedness of the multilinear Riesz potential operator  on the homogeneous Morrey-Herz spaces.
on the homogeneous Morrey-Herz spaces.
Theorem 1.2.
Let  ,
,  ,
,  ,
,  and
and  for
for  . Suppose that
. Suppose that  ,
,  ,
,  ,
,  then
then

with a constant  independent of
independent of  .
.
In the case  for
for  , we will use the weak homogeneous Morrey-Herz spaces
, we will use the weak homogeneous Morrey-Herz spaces  and weak homogeneous Herz spaces
and weak homogeneous Herz spaces  to derive the following boundedness for the operator
to derive the following boundedness for the operator  .
.
Theorem 1.3.
Let  ,
,  ,
,  and
and  for
for  . Suppose that
. Suppose that  ,
,  ,
,  then
then

with a constant  independent of
independent of  .
.
Remark 1.4.
The restriction  in Theorem 1.3 cannot be removed see [9] for an counter-example when
in Theorem 1.3 cannot be removed see [9] for an counter-example when  and
and  .
.
In addition, we remark that the (weak) homogeneous Morrey-Herz spaces generalize the (weak) homogeneous Herz spaces. Particularly,  and
and  for
for  and
and  . Moreover, we have
. Moreover, we have  , the weighted
, the weighted  spaces
spaces  for
for  and
and  , for details, see Section 2.
, for details, see Section 2.
Hence, it is easy to obtain the following corollaries from the theorems above.
Corollary 1.5.
Let  ,
,  ,
,  .
.
-
(i)
If
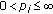 ,
,  ,
, 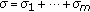 with
with 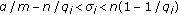 for
for 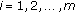 . Then
. Then

with a constant  independent of
independent of  .
.
-
(ii)
If
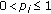 and
and 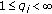 for
for  then
then

with a constant  independent of
independent of  .
.
Corollary 1.6.
Let 
 with
with 
 with
with  for
for  then
then

with a constant  independent of
independent of  .
.
Throughout this paper, the letter  always remains to denote a positive constant that may vary at each occurrence but is independent of all essential variables.
always remains to denote a positive constant that may vary at each occurrence but is independent of all essential variables.
2. The Definitions of Some Function Spaces
We start with some notations and definitions. Here and in what follows, denote by  ,
,  and
and  for
for  the characteristic function of the set
the characteristic function of the set  .
.
Definition 2.1.
Let  ,
,  and
and  . The homogeneous Herz spaces
. The homogeneous Herz spaces  are defined to be the following space of functions:
are defined to be the following space of functions:

where

and the usual modification should be made when  .
.
Definition 2.2.
Let  ,
,  and
and  . The weak homogeneous Herz spaces
. The weak homogeneous Herz spaces  are defined by
are defined by

where

and the usual modification should be made when  .
.
Definition 2.3.
Let  ,
,  ,
,  and
and  . The homogeneous Morrey-Herz spaces
. The homogeneous Morrey-Herz spaces  are defined by
are defined by

where

and the usual modifications should be made when  .
.
Definition 2.4.
Let  ,
,  ,
,  and
and  . The weak homogeneous Morrey-Herz spaces
. The weak homogeneous Morrey-Herz spaces  are defined by
are defined by

where

and the usual modifications should be made when  .
.
3. Proof of Theorems 1.2 and 1.3
Without loss of generality, in order to simplify the proof, we only consider the situation when  . Actually, the similar procedure works for all
. Actually, the similar procedure works for all  .
.
Indeed, we decompose  as
as

To shorten the formulas below, we set

It is easy to see that the case for  is analogous to the case for
is analogous to the case for  , the case for
, the case for  is similar to the case for
is similar to the case for  , and the case for
, and the case for  is analogous to the case for
is analogous to the case for  , respectively. Thus, by the symmetry of
, respectively. Thus, by the symmetry of  and
and  in the operator
in the operator  , we will only discuss the cases for
, we will only discuss the cases for  belong to
belong to  ,
,  ,
,  ,
,  ,
,  and
and  , respectively.
, respectively.
By a direct computation, we have the following fact that, for  ,
,

We will use estimates (3.3) in the proof of theorems below. In addition, we always let  ,
,  ,
,  for
for  , and use the notations
, and use the notations

It is easy to see that  when
when  , and that
, and that  when
when  .
.
We will also use repeatedly the inequality  for
for  .
.
Now we are ready to the proof of Theorem 1.2. Suppose that  , by the decomposition of
, by the decomposition of  above, we get
above, we get

where

To estimate the term  , we first note that inequality (3.3) and the growth condition (1.2) of
, we first note that inequality (3.3) and the growth condition (1.2) of  imply that
imply that

Hence, by the fact  , the Cauchy inequality and the growth condition (1.2) of
, the Cauchy inequality and the growth condition (1.2) of  , we can show that
, we can show that

where

In case  , using the fact
, using the fact  , we have
, we have

In case  , using the Hölder inequality, we get
, using the Hölder inequality, we get

In case  , recalling the definition of Morrey-Herz spaces we get
, recalling the definition of Morrey-Herz spaces we get

Therefore, for any  , we have obtained that
, we have obtained that

For  , by the growth condition (1.2) of
, by the growth condition (1.2) of  , inequality (3.3) and the Cauchy inequality, we use the analogous arguments as that of
, inequality (3.3) and the Cauchy inequality, we use the analogous arguments as that of  to deduce that
to deduce that

We observe that  is equal to
is equal to  , and so we have
, and so we have

with a constant  independent of
independent of  .
.
For  , noting that
, noting that  , one can see easily that
, one can see easily that

with a constant  independent of
independent of  .
.
Combining inequalities (3.15) and (3.16), we obtain

For  , by using the growth condition (1.2) of
, by using the growth condition (1.2) of  , estimate (3.3), and the Cauchy inequality, we obtain
, estimate (3.3), and the Cauchy inequality, we obtain

Noting that  , by (3.15), we get
, by (3.15), we get

with a constant  independent of
independent of  .
.
As for  , we can also write
, we can also write

Now, we estimate  and
and  respectively. For
respectively. For  , using similar methods as that for
, using similar methods as that for  , we consider the following three cases.
, we consider the following three cases.
If  , the fact
, the fact  implies that
implies that

If  , the Hölder inequality and the fact
, the Hölder inequality and the fact  yield that
yield that

If  , we get
, we get

Thus, we get

with a constant  independent of
independent of  .
.
For  , by the fact
, by the fact  , we have
, we have

Therefore, the inequality above and inequalities (3.19), (3.20), and (3.24) yield

To estimate the term  , using Proposition 1.1, the
, using Proposition 1.1, the  -boundedness for
-boundedness for  , we obtain
, we obtain

Thus, a similar argument shows that

For  , by condition (1.2) and inequality (3.3), we have
, by condition (1.2) and inequality (3.3), we have

Finally to estimate the term  , by the Hölder inequality, condition (1.2), and inequality (3.3), one sees that
, by the Hölder inequality, condition (1.2), and inequality (3.3), one sees that

Combining all the estimates for  for
for  , we get
, we get

This is the desired estimate of Theorem 1.2.
The proof of Theorem 1.2 is completed.
Next we turn to the proof of Theorem 1.3. Let  ,
,  be functions in
be functions in  and
and  respectively. Obviously, to prove the theorem, we only need to find a constant
respectively. Obviously, to prove the theorem, we only need to find a constant  independent of
independent of  such that
such that

for all  .
.
By the decomposition of  above, we get
above, we get

where

Similar to the proof of Theorem 1.2, we only need to estimate  ,
,  ,
,  ,
,  ,
,  and
and  respectively.
respectively.
For  , using the Chebychev inequality, the Hölder inequality, (1.2), and (3.3), we obtain
, using the Chebychev inequality, the Hölder inequality, (1.2), and (3.3), we obtain

Therefore, the facts  ,
,  and the Cauchy inequality imply that
and the Cauchy inequality imply that

Now, we consider the estimate of the term  . Using a similar argument as that of
. Using a similar argument as that of  , we can deduce that
, we can deduce that

as desired.
To estimate  , we point out the fact
, we point out the fact

So we can show that

From the estimates of  , we know
, we know  , so we only need to show that
, so we only need to show that  .
.
For  , we write
, we write

First, the fact  yields that
yields that

Second, the fact  implies
implies

as desired.
To estimate the term  , by Proposition 1.1, the weak
, by Proposition 1.1, the weak  -boundedness for
-boundedness for  , we obtain
, we obtain

Similar to the estimates of  , we have
, we have

For  , we obtain
, we obtain

Finally, we have to estimate the term  . It can be deduced that
. It can be deduced that

Here the estimate of  and
and  is similar to that of
is similar to that of  .
.
Finally, a combination for the estimates of  (
( ) finishes the proof of Theorem 1.3.
) finishes the proof of Theorem 1.3.
References
García-Cuerva J, Martell JM: Two-weight norm inequalities for maximal operators and fractional integrals on non-homogeneous spaces. Indiana University Mathematics Journal 2001, 50(3):1241–1280.
Sawano Y, Tanaka H: Morrey spaces for non-doubling measures. Acta Mathematica Sinica 2005, 21(6):1535–1544. 10.1007/s10114-005-0660-z
Xu J: Boundedness of multilinear singular integrals for non-doubling measures. Journal of Mathematical Analysis and Applications 2007, 327(1):471–480. 10.1016/j.jmaa.2006.04.049
Lian J, Wu H: A class of commutators for multilinear fractional integrals in nonhomogeneous spaces. Journal of Inequalities and Applications 2008, 2008:-17.
Kenig CE, Stein EM: Multilinear estimates and fractional integration. Mathematical Research Letters 1999, 6(1):1–15.
Tao XX, Shi YL, Zhang SY: Boundedness of multilinear Riesz potential on the product of Morrey and Herz-Morrey spaces. Acta Mathematica Sinica. Chinese Series 2009, 52(3):535–548.
Shi Y, Tao X: Boundedness for multilinear fractional integral operators on Herz type spaces. Applied Mathematics, Journal of Chinese Universities B 2008, 23(4):437–446. 10.1007/s11766-008-1995-x
Shi Y, Tao X: Multilinear Riesz potential operators on Herz-type spaces and generalized Morrey spaces. Hokkaido Mathematical Journal 2009, 38(4):635–662.
Komori Y: Weak type estimates for Calderón-Zygmund operators on Herz spaces at critical indexes. Mathematische Nachrichten 2003, 259: 42–50. 10.1002/mana.200310093
Acknowledgment
This work was supported partly by the National Natural Science Foundation of China under Grant no. 10771110 and sponsored by the Natural Science Foundation of Ningbo City under Grant no. 2009A610084.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shi, Y., Tao, X. & Zheng, T. Multilinear Riesz Potential on Morrey-Herz Spaces with Non-Doubling Measures. J Inequal Appl 2010, 731016 (2010). https://doi.org/10.1155/2010/731016
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/731016



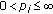 ,
,  ,
, 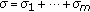 with
with 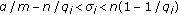 for
for 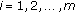 . Then
. Then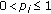 and
and 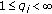 for
for  then
then