Abstract
An operator  is called
is called  -quasiclass
-quasiclass  if
if  for a positive integer
for a positive integer  , which is a common generalization of quasiclass
, which is a common generalization of quasiclass  . In this paper, firstly we prove some inequalities of this class of operators; secondly we prove that if
. In this paper, firstly we prove some inequalities of this class of operators; secondly we prove that if  is a
is a  -quasiclass
-quasiclass  operator, then
operator, then  is isoloid and
is isoloid and  has finite ascent for all complex number
has finite ascent for all complex number  at last we consider the tensor product for
at last we consider the tensor product for  -quasiclass
-quasiclass  operators.
operators.
Similar content being viewed by others
1. Introduction
Throughout this paper let  be a separable complex Hilbert space with inner product
be a separable complex Hilbert space with inner product  . Let
. Let  denote the
denote the  -algebra of all bounded linear operators on
-algebra of all bounded linear operators on  .
.
Let  and let
and let  be an isolated point of
be an isolated point of  . Here
. Here  denotes the spectrum of
denotes the spectrum of  . Then there exists a small enough positive number
. Then there exists a small enough positive number  such that
such that

Let


is called the Riesz idempotent with respect to  , and it is well known that
, and it is well known that  satisfies
satisfies  ,
,  ,
,  , and
, and  for all positive integers
for all positive integers  . Stampfli [1] proved that if
. Stampfli [1] proved that if  is hyponormal (i.e., operators such that
is hyponormal (i.e., operators such that  ), then
), then

After that many authors extended this result to many other classes of operators. Chō and Tanahashi [2] proved that (1.3) holds if  is either
is either  -hyponormal or log-hyponormal. In the case
-hyponormal or log-hyponormal. In the case  , the result was further shown by Tanahashi and Uchiyama [3] to hold for
, the result was further shown by Tanahashi and Uchiyama [3] to hold for  -quasihyponormal operators, by Tanahashi et al. [4] to hold for
-quasihyponormal operators, by Tanahashi et al. [4] to hold for  -quasihyponormal operators and by Uchiyama and Tanahashi [5] and Uchiyama [6] for class A and paranormal operators. Here an operator
-quasihyponormal operators and by Uchiyama and Tanahashi [5] and Uchiyama [6] for class A and paranormal operators. Here an operator  is called
is called  -hyponormal for
-hyponormal for  if
if  , and log-hyponormal if
, and log-hyponormal if  is invertible and
is invertible and  . An operator
. An operator  is called
is called  -quasihyponormal if
-quasihyponormal if  , where
, where  and
and  is a positive integer; especially, when
is a positive integer; especially, when  ,
,  , and
, and  ,
,  is called
is called  -quasihyponormal,
-quasihyponormal,  -quasihyponormal, and quasihyponormal, respectively. And an operator
-quasihyponormal, and quasihyponormal, respectively. And an operator  is called paranormal if
is called paranormal if  for all
for all  ; normaloid if
; normaloid if  for all positive integers
for all positive integers  .
.  -hyponormal, log-hyponormal,
-hyponormal, log-hyponormal,  -quasihyponormal,
-quasihyponormal,  -quasihyponormal, and paranormal operators were introduced by Aluthge [7], Tanahashi [8], S. C. Arora and P. Arora [9], Kim [10], and Furuta [11, 12], respectively.
-quasihyponormal, and paranormal operators were introduced by Aluthge [7], Tanahashi [8], S. C. Arora and P. Arora [9], Kim [10], and Furuta [11, 12], respectively.
In order to discuss the relations between paranormal and  -hyponormal and log-hyponormal operators, Furuta et al. [13] introduced a very interesting class of bounded linear Hilbert space operators: class A defined by
-hyponormal and log-hyponormal operators, Furuta et al. [13] introduced a very interesting class of bounded linear Hilbert space operators: class A defined by  , where
, where  which is called the absolute value of
which is called the absolute value of  and they showed that class A is a subclass of paranormal and contains
and they showed that class A is a subclass of paranormal and contains  -hyponormal and log-hyponormal operators. Class A operators have been studied by many researchers, for example, [5, 14–19].
-hyponormal and log-hyponormal operators. Class A operators have been studied by many researchers, for example, [5, 14–19].
Recently Jeon and Kim [20] introduced quasiclass A (i.e.,  ) operators as an extension of the notion of class A operators, and they also proved that (1.3) holds for this class of operators when
) operators as an extension of the notion of class A operators, and they also proved that (1.3) holds for this class of operators when  . It is interesting to study whether Stampli's result holds for other larger classes of operators.
. It is interesting to study whether Stampli's result holds for other larger classes of operators.
In [21], Tanahashi et al. considered an extension of quasi-class A operators, similar in spirit to the extension of the notion of  -quasihyponormality to
-quasihyponormality to  -quasihyponormality, and prove that (1.3) holds for this class of operators in the case
-quasihyponormality, and prove that (1.3) holds for this class of operators in the case  .
.
Definition 1.1.

is called a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  if
if

Remark 1.2.
In [21], this class of operators is called quasi-class (A,  ).
).
It is clear that the class of quasi-class A operators
A operators the class of k-quasiclass A operators and
the class of k-quasiclass A operators and

We show that the inclusion relation (1.5) is strict, by an example which appeared in [20].
Example 1.3.
Given a bounded sequence of positive numbers  , let
, let  be the unilateral weighted shift operator on
be the unilateral weighted shift operator on  with the canonical orthonormal basis
with the canonical orthonormal basis  by
by  for all
for all  , that is,
, that is,

Straightforward calculations show that  is a
is a  -quasiclass A operator if and only if
-quasiclass A operator if and only if  . So if
. So if  and
and  , then
, then  is a
is a  -quasiclass A operator, but not a
-quasiclass A operator, but not a  -quasiclass A operator.
-quasiclass A operator.
In this paper, firstly we consider some inequalities of  -quasiclass A operators; secondly we prove that if
-quasiclass A operators; secondly we prove that if  is a
is a  -quasiclass A operator, then
-quasiclass A operator, then  is isoloid and
is isoloid and  has finite ascent for all complex number
has finite ascent for all complex number  ; at last we give a necessary and sufficient condition for
; at last we give a necessary and sufficient condition for  to be a
to be a  -quasiclass A operator when
-quasiclass A operator when  and
and  are both non-zero operators.
are both non-zero operators.
2. Results
In the following lemma, Tanahashi, Jeon, Kim, and Uchiyama studied the matrix representation of a  -quasiclass A operator with respect to the direct sum of
-quasiclass A operator with respect to the direct sum of  and its orthogonal complement.
and its orthogonal complement.
Lemma 2.1 (see [21]).
Let  be a
be a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  and let
and let  on
on  be
be  matrix expression. Assume that ran
matrix expression. Assume that ran is not dense, then
is not dense, then  is a class A operator on
is a class A operator on  and
and  . Furthermore,
. Furthermore,  .
.
Proof.
Consider the matrix representation of  with respect to the decomposition
with respect to the decomposition  :
:  Let
Let  be the orthogonal projection of
be the orthogonal projection of  onto
onto  . Then
. Then  . Since
. Since  is a
is a  -quasiclass A operator, we have
-quasiclass A operator, we have

Then

by Hansen's inequality [22]. On the other hand

Hence

That is,  is a class A operator on
is a class A operator on  .
.
For any  ,
,

which implies  .
.
Since  , where
, where  is the union of the holes in
is the union of the holes in  which happen to be subset of
which happen to be subset of  by [23, Corollary 7], and
by [23, Corollary 7], and  and
and  has no interior points, we have
has no interior points, we have  .
.
Theorem 2.2.
Let  be a
be a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  . Then the following assertions hold.
. Then the following assertions hold.
 for all
for all  and all positive integers
and all positive integers  .
.
If  for some positive integer
for some positive integer  , then
, then  .
.
 for all positive integers
for all positive integers  , where
, where  denotes the spectral radius of
denotes the spectral radius of  .
.
To give a proof of Theorem 2.2, the following famous inequality is needful.
Lemma 2.3 (Hölder-McCarthy's inequality [24]).
Let  . Then the following assertions hold.
. Then the following assertions hold.
 for
for  and all
and all  .
.
 for
for  and all
and all  .
.
Proof of Theorem 2.2.
-
(1)
Since it is clear that
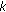 -quasiclass A operators are
-quasiclass A operators are 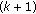 -quasiclass A operators, we only need to prove the case
-quasiclass A operators, we only need to prove the case 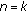 . Since
. Since 
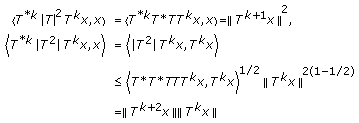 (2.6)
(2.6)
by Hölder-McCarthy's inequality, we have

for  is a
is a  -quasiclass A operator.
-quasiclass A operator.
-
(2)
If
 , it is obvious that
, it is obvious that 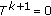 . If
. If 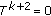 , then
, then 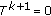 by (
by ( ). The rest of the proof is similar.
). The rest of the proof is similar. -
(3)
We only need to prove the case
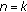 , that is,
, that is,

If  for some
for some  , then
, then  by (2) and in this case
by (2) and in this case  . Hence (3) is clear. Therefore we may assume
. Hence (3) is clear. Therefore we may assume  for all
for all  . Then
. Then

by ( ), and we have
), and we have

Hence

By letting  , we have
, we have

that is,

Lemma 2.4 (see [21]).
Let  be a
be a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  . If
. If  and
and  for some
for some  , then
, then  .
.
Proof.
We may assume that  . Let
. Let  be a span of
be a span of  . Then
. Then  is an invariant subspace of
is an invariant subspace of  and
and

Let  be the orthogonal projection of
be the orthogonal projection of  onto
onto  . It suffices to show that
. It suffices to show that  in (2.14). Since
in (2.14). Since  is a
is a  -quasiclass A operator, and
-quasiclass A operator, and 
 , we have
, we have

We remark

Then by Hansen's inequality and (2.15), we have

Hence we may write

We have

This implies  and
and  . On the other hand,
. On the other hand,

Hence  and
and  . Since
. Since  is a
is a  -quasiclass A operator, by a simple calculation we have
-quasiclass A operator, by a simple calculation we have

Recall that  if and only if
if and only if  and
and  for some contraction
for some contraction  . Thus we have
. Thus we have  . This completes the proof.
. This completes the proof.
Lemma 2.5 (see [25]).
If  satisfies
satisfies  for some complex number
for some complex number  , then
, then  for any positive integer
for any positive integer  .
.
Proof.
It suffices to show  by induction. We only need to show
by induction. We only need to show  since
since  is clear. In fact, if
is clear. In fact, if  , then we have
, then we have  by hypothesis. So we have
by hypothesis. So we have  , that is,
, that is,  . Hence
. Hence  .
.
An operator is said to have finite ascent if  for some positive integer
for some positive integer  .
.
Theorem 2.6.
Let  be a
be a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  . Then
. Then  has finite ascent for all complex number
has finite ascent for all complex number  .
.
Proof.
We only need to show the case  because the case
because the case  holds by Lemmas 2.4 and 2.5.
holds by Lemmas 2.4 and 2.5.
In the case  , we shall show that
, we shall show that  . It suffices to show that
. It suffices to show that  since
since  is clear. Now assume that
is clear. Now assume that  . We may assume
. We may assume  since if
since if  , it is obvious that
, it is obvious that  . By Hölder-McCarthy's inequality, we have
. By Hölder-McCarthy's inequality, we have

So we have  , which implies
, which implies  . Therefore
. Therefore  .
.
In the following lemma, Tanahashi, Jeon, Kim, and Uchiyama extended the result (1.3) to  -quasiclass A operators in the case
-quasiclass A operators in the case  .
.
Lemma 2.7 (see [21]).
Let  be a
be a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  . Let
. Let  be an isolated point of
be an isolated point of  and
and  the Riesz idempotent for
the Riesz idempotent for  . Then the following assertions hold.
. Then the following assertions hold.
If  , then
, then  is self-adjoint and
is self-adjoint and

If  , then
, then  .
.
An operator  is said to be isoloid if every isolated point of
is said to be isoloid if every isolated point of  is an eigenvalue of
is an eigenvalue of  .
.
Theorem 2.8.
Let  be a
be a  -quasiclass A operator for a positive integer
-quasiclass A operator for a positive integer  . Then
. Then  is isoloid.
is isoloid.
Proof.
Let  be an isolated point. If
be an isolated point. If  , by (
, by ( ) of Lemma 2.7,
) of Lemma 2.7,  for
for  . Therefore
. Therefore  is an eigenvalue of
is an eigenvalue of  . If
. If  , by (
, by ( ) of Lemma 2.7,
) of Lemma 2.7,  for
for  . So we have
. So we have  . Therefore
. Therefore  is an eigenvalue of
is an eigenvalue of  . This completes the proof.
. This completes the proof.
Let  denote the tensor product on the product space
denote the tensor product on the product space  for nonzero
for nonzero  ,
,  . The following theorem gives a necessary and sufficient condition for
. The following theorem gives a necessary and sufficient condition for  to be a
to be a  -quasiclass A operator, which is an extension of [20, Theorem 4.2].
-quasiclass A operator, which is an extension of [20, Theorem 4.2].
Theorem 2.9.
Let  ,
,  be nonzero operators. Then
be nonzero operators. Then  is a
is a  -quasiclass A operator if and only if one of the following assertions holds
-quasiclass A operator if and only if one of the following assertions holds
(1) or
or  .
.
(2) and
and  are
are  -quasiclass A operators.
-quasiclass A operators.
Proof.
It is clear that  is a
is a  -quasiclass A operator if and only if
-quasiclass A operator if and only if

Therefore the sufficiency is clear.
To prove the necessary, suppose that  is a
is a  -quasiclass A operator. Let
-quasiclass A operator. Let  ,
,  be arbitrary. Then we have
be arbitrary. Then we have

It suffices to prove that if ( ) does not hold, then (
) does not hold, then ( ) holds. Suppose that
) holds. Suppose that  and
and  . To the contrary, assume that
. To the contrary, assume that  is not a
is not a  -quasiclass A operator, then there exists
-quasiclass A operator, then there exists  such that
such that

From (2.25) we have

that is,

for all  . Therefore
. Therefore  is a
is a  -quasiclass A operator. As the proof in Theorem 2.2 (
-quasiclass A operator. As the proof in Theorem 2.2 ( ), we have
), we have

So we have

for all  by (2.28). Because
by (2.28). Because  is a
is a  -quasiclass A operator, from Lemma 2.1 we can write
-quasiclass A operator, from Lemma 2.1 we can write  on
on  , where
, where  is a class A operator (hence it is normaloid). By (2.30) we have
is a class A operator (hence it is normaloid). By (2.30) we have

So we have

where equality holds since  is normaloid.
is normaloid.
This implies that  . Since
. Since  for all
for all  , we have
, we have  . This contradicts the assumption
. This contradicts the assumption  . Hence
. Hence  must be a
must be a  -quasiclass A operator. A similar argument shows that
-quasiclass A operator. A similar argument shows that  is also a
is also a  -quasiclass A operator. The proof is complete.
-quasiclass A operator. The proof is complete.
References
Stampfli JG: Hyponormal operators and spectral density. Transactions of the American Mathematical Society 1965, 117: 469–476.
Chō M, Tanahashi K: Isolated point of spectrum of -hyponormal, log-hyponormal operators. Integral Equations and Operator Theory 2002,43(4):379–384. 10.1007/BF01212700
Tanahashi K, Uchiyama A: Isolated point of spectrum of -quasihyponormal operators. Linear Algebra and Its Applications 2002, 341: 345–350. 10.1016/S0024-3795(01)00476-1
Tanahashi K, Uchiyama A, Chō M: Isolated points of spectrum of -quasihyponormal operators. Linear Algebra and Its Applications 2004, 382: 221–229.
Uchiyama A, Tanahashi K: On the Riesz idempotent of class operators. Mathematical Inequalities & Applications 2002,5(2):291–298.
Uchiyama A: On the isolated points of the spectrum of paranormal operators. Integral Equations and Operator Theory 2006,55(1):145–151. 10.1007/s00020-005-1386-0
Aluthge A: On -hyponormal operators for . Integral Equations and Operator Theory 1990,13(3):307–315. 10.1007/BF01199886
Tanahashi K: On log-hyponormal operators. Integral Equations and Operator Theory 1999,34(3):364–372. 10.1007/BF01300584
Arora SC, Arora P: On -quasihyponormal operators for . Yokohama Mathematical Journal 1993,41(1):25–29.
Kim IH: On -quasihyponormal operators. Mathematical Inequalities & Applications 2004,7(4):629–638.
Furuta T: On the class of paranormal operators. Proceedings of the Japan Academy 1967, 43: 594–598. 10.3792/pja/1195521514
Furuta T: Invitation to Linear Operators: From Matrices to Bounded Linear Operators on a Hilbert Space. Taylor & Francis, London, UK; 2001:x+255.
Furuta T, Ito M, Yamazaki T: A subclass of paranormal operators including class of log-hyponormal and several related classes. Scientiae Mathematicae 1998,1(3):389–403.
Chō M, Giga M, Huruya T, Yamazaki T: A remark on support of the principal function for class operators. Integral Equations and Operator Theory 2007,57(3):303–308. 10.1007/s00020-006-1463-z
Chō M, Yamazaki T: An operator transform from class to the class of hyponormal operators and its application. Integral Equations and Operator Theory 2005,53(4):497–508. 10.1007/s00020-004-1332-6
Ito M: Several properties on class including -hyponormal and log-hyponormal operators. Mathematical Inequalities & Applications 1999,2(4):569–578.
Ito M, Yamazaki T: Relations between two inequalities and and their applications. Integral Equations and Operator Theory 2002,44(4):442–450. 10.1007/BF01193670
Uchiyama A: Weyl's theorem for class operators. Mathematical Inequalities & Applications 2001,4(1):143–150.
Wang D, Lee JI: Spectral properties of class operators. Trends in Mathematics Information Center for Mathematical Sciences 2003,6(2):93–98.
Jeon IH, Kim IH: On operators satisfying . Linear Algebra and Its Applications 2006,418(2–3):854–862. 10.1016/j.laa.2006.02.040
Tanahashi K, Jeon IH, Kim IH, Uchiyama A: Quasinilpotent part of class or -quasihyponormal operators. Operator Theory: Advances and Applications 2008, 187: 199–210.
Hansen F: An operator inequality. Mathematische Annalen 1980,246(3):249–250. 10.1007/BF01371046
Han JK, Lee HY, Lee WY: Invertible completions of upper triangular operator matrices. Proceedings of the American Mathematical Society 2000,128(1):119–123. 10.1090/S0002-9939-99-04965-5
McCarthy CA: “
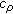 ” . Israel Journal of Mathematics 1967, 5: 249–271. 10.1007/BF02771613
” . Israel Journal of Mathematics 1967, 5: 249–271. 10.1007/BF02771613Han YM, Lee JI, Wang D: Riesz idempotent and Weyl's theorem for -hyponormal operators. Integral Equations and Operator Theory 2005,53(1):51–60. 10.1007/s00020-003-1313-1
Acknowledgments
The authors would like to express their cordial gratitude to the referee for his useful comments and Professor K. Tanahashi and Professor I. H. Jeon for sending them [21]. This research is supported by the National Natural Science Foundation of China (no. 10771161).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gao, F., Fang, X. On 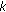 -Quasiclass A Operators.
J Inequal Appl 2009, 921634 (2009). https://doi.org/10.1155/2009/921634
-Quasiclass A Operators.
J Inequal Appl 2009, 921634 (2009). https://doi.org/10.1155/2009/921634
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/921634



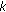 -quasiclass A operators are
-quasiclass A operators are 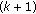 -quasiclass A operators, we only need to prove the case
-quasiclass A operators, we only need to prove the case 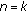 . Since
. Since 
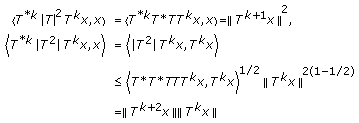
 , it is obvious that
, it is obvious that 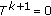 . If
. If 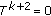 , then
, then 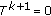 by (
by ( ). The rest of the proof is similar.
). The rest of the proof is similar.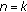 , that is,
, that is,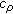 ” . Israel Journal of Mathematics 1967, 5: 249–271. 10.1007/BF02771613
” . Israel Journal of Mathematics 1967, 5: 249–271. 10.1007/BF02771613