1 Introduction

Propagation of waves in fluids can produce not only energy transfer from one point to another, but also a displacement of the fluid along the propagation axis (a wave matter transport). This drift is a nonlinear effect investigated theoretically in Refs. [1,2,3,4,5], which can explain, for example, the formation of stellar winds in cosmic space [2,3,4,5].

The transport of the media can be also realized through waves excited by horizontal vibrations of the channel walls or ground. In earlier work [6], we showed that such a mean mass flow emerges if the lateral excitation are asymmetric under time reversal, e.g., taking a ratchet shape instead of a harmonic one. Another symmetry breaking mechanism can be provided by a lateral temperature gradient [7, 8].

In the present study, we shall focus on an asymmetric periodic vibration of a liquid channel with an immersed mirror-symmetric obstacle fixed to the bottom, extending our previous work from Ref. [9]. The obstacle is always completely covered by the fluid. Such problems might have widespread applications for controlled sediment transport in rivers, lakes or oceans. Our investigation is mainly motivated by experiments outlined in the first part. In the second part, we derive a long-wave model adjusted to our experimental device and present numerical solutions of the wave shapes and of the mean flow, depending on the driving frequency and the asymmetry parameter of the acceleration.

2 Experiments

2.1 Statement of the problem and experimental apparatus

We aim to study quasi-two-dimensional water waves propagating and interacting with themselves. This kind of interaction commonly leads to a resonant response. The experiments are performed in a narrow channel filled with water, as presented in Fig. 1a. To avoid reflections at endwalls in the flow direction, an ideal choice would be periodic boundary conditions. Although easily realized in theoretical or numerical studies, it is not straightforward in experiments. To close the domain, we use an annular channel placed on a rotating table (Fig. 1b). The rotation axis and the channel symmetry axis coincide. Rotation implies the existence of centrifugal and Coriolis forces. However, if the fluid velocities are moderate and the curvature of the channel is small, the effect of these forces can be neglected.

The channel is filled with a 5 cm deep water layer, its length (measured in the middle of the channel) is \({{\tilde{L}}}=476\) cm and its width is 8.5 cm. An obstacle of 2 cm height and 30 cm width is placed on the channel’s bottom (see Fig. 1a). The obstacle is mirror symmetric and plays the role of a wave maker during the periodic oscillations of the channel along its length. To produce a net mean flow (mass transport), a left/right asymmetry must be introduced in the system. For the actual investigation, the asymmetry will be produced by anharmonic channel oscillations. The acceleration of the oscillatory rotating tank with respect to the laboratory frame \({{\tilde{a}}}({{\tilde{t}}})\) has a shape inspired from the saw tooth. To violate the symmetry \(\tilde{a}({{\tilde{t}}})={{\tilde{a}}}({{\tilde{t}}}_0-{{\tilde{t}}}),\) it is sufficient to take only the first two terms of the Fourier series which converge to the saw tooth function, namely, to add to the fundamental harmonic of frequency \({{\tilde{f}}}\) a second one of double frequency:

$$\begin{aligned} {{\tilde{a}}}({{\tilde{t}}})={{\tilde{a}}}_0(\sin ({{\tilde{\omega }}}{{\tilde{t}}})+\alpha \sin (2{{\tilde{\omega }}}{{\tilde{t}}})), \end{aligned}$$
(1)

where \({{\tilde{\omega }}}=2\pi {{\tilde{f}}}\) is the angular excitation frequency and \(\alpha =\pm 1/2\) for the saw tooth function expansion.

Fig. 1
figure 1

(a) The sketch of the setup. A two-dimensional problem under periodic boundary condition is considered. (b) General view of the tank placed on a rotating table. The outer channel marked with a red arrow is used to study surface waves and their interactions (for more details regarding the experimental setup, see Ref. [10])

Full size image

We wish to study the formation of waves for a wide region of the excitation frequency f. For technical reasons, we keep the maximum velocity of the excitation constant and by taking

$$\begin{aligned} {{\tilde{a}}}_0 = b\;{{\tilde{f}}} \end{aligned}$$
(2)

with \(b=0.65\) m/s leads to the maximal velocity of \(\tilde{v}_{max1}=b/(2\pi )\) for the fundamental harmonic and \(\tilde{v}_{max2}=b/(4\pi )\) for the double frequency. This results in a maximal total velocity of about 0.16 m/s. The maximal centrifugal acceleration is thus two orders of magnitude smaller than the gravity. Therefore in our study, the curvature can be neglected. For this study, we use only data from videos recorded with a Go-Pro Hero 4 camera with a 8 mm rectilinear custom objective. The camera is located on the opposite side of the obstacle, and the channel is illuminated with a green 75 mW MediaLas laser sheet. The resolution is \(1920\times 1800\) pixels, and the frame rate is 60 frames/s. A mixture of \(1~\mu\)m silver-covered and non-covered glass spheres is diffused in water and used as PIV trackers. Close to the bottom and the water/air interface, the light intensity is higher, see Fig. 2. The PIV velocities are calculated applying PIVmat app of MATLAB R2021a.

Fig. 2
figure 2

One frame from the Go-Pro camera. The lighter regions designate the channel’s bottom and the water surface in the middle of the circular channel. The arrows represent the velocities calculated with the PIV method. The boundary layer of around \(h_b=2\) mm has been eliminated from the flow calculation

Full size image

2.2 Experimental results

From the surface deflection \({{\tilde{h}}}-{{\tilde{h}}}_0,\) one finds the quantity:

$$\begin{aligned} \langle ({{\tilde{h}}}-{{\tilde{h}}}_0)^2\rangle ({{\tilde{x}}})=\frac{1}{\tilde{T}}\int _0^{{{\tilde{T}}}} ({{\tilde{h}}}(x,t)-{{\tilde{h}}}_0)^2\,d{{\tilde{t}}}, \qquad {{\tilde{T}}}=2\pi /{{\tilde{\omega }}}, \end{aligned}$$
(3)

which is related to the potential energy. During the wave–wave interaction, we expect to have regions with nodes (with minimum of amplitude and energy) and antinodes (with maximum of amplitude and energy) whose positions may vary with frequency. To reduce this effect, we plot the maximum value of (3) along the x coordinate from the camera cut across from the obstacle of about 23 cm (blue curve in Fig. 3).

The question is now to see how far an anharmonic lateral excitation of the form (1) can cause a mass transport through the channel. To this end, a method measuring the mean flow is developed. The mean flow is expected to be much smaller than the instantaneous flow produced by the tank oscillations. Therefore, a lot of attention should be paid to minimize the errors. We first calculate the instantaneous flux with the camera time resolution of 1/60 s. For our experiments, the boundary layer is of the order \(h_b=2\) mm. The PIV measurements of the horizontal velocity component \({{\tilde{u}}}\) are not precise near the bottom boundary and near the surface. Also, we found that the velocity profile in the fluid bulk is almost constant in the vertical direction and is well resolved by the PIV algorithm. The surface deformation is taken into account at each moment of time and each horizontal \({{\tilde{x}}}\) coordinate. To calculate the instantaneous flux

$$\begin{aligned} {{\tilde{\Phi }}}({{\tilde{x}}},{{\tilde{t}}})=\int _{h_b}^{{{\tilde{h}}}} {{\tilde{u}}}(\tilde{x},{{\tilde{z}}},{{\tilde{t}}})\, d{{\tilde{z}}}, \end{aligned}$$
(4)

we apply a linear extrapolation in the vertical direction of the velocity field from the boundary layer limit to the surface. If the flow is time periodic, the time mean

$$\begin{aligned} \overline{{{{\tilde{\Phi }}}}}({{\tilde{x}}})=\frac{1}{{{\tilde{T}}}}\,\int _0^{\tilde{T}} {{\tilde{\Phi }}}({{\tilde{x}}},{{\tilde{t}}})\, d{{\tilde{t}}}, \end{aligned}$$
(5)

should not depend on \({{\tilde{x}}}\) due to mass conservation. Finally, the flux (5) is averaged with respect to \(\tilde{x}\) to minimize the errors. The \({{\tilde{x}}}\) and \({{\tilde{t}}}\) averaged measured volume flux is plotted in red in Fig. 3.

Resonance curves in terms of mean square surface deflection have been already studied in [9]. Because the study has been performed for the case of solid barriers, only reflection modes were found. Those modes correspond to odd multiples of the fundamental frequency \(f_0\). Using a simple intuitive model, it was shown that the period of the fundamental mode is roughly the time for the wave to travel forth and back along the channel: \(\tilde{T}_0=2{{\tilde{L}}}/{{\tilde{c}}}_0\), where \({{\tilde{c}}}_0\) is the shallow water wave velocity. Mean flow was not possible due to the barriers that completely blocked the flow. For the actual study, the bottom elevation permits also wave transmission and mean flow. For this reason, also even multiples of the fundamental frequency \(f_0\) can be found. The first transmission mode has a period given by the one time travel of the channel length (\({{\tilde{T}}}_{1,transm}=\tilde{L}/{{\tilde{c}}}_0\) and \({{\tilde{f}}}_{1,transm}=2{{\tilde{f}}}_0\)). The wave will reach the bottom elevation when both move in the same direction and thus will be enhanced. Because of the non-linear effects, a flow can be driven by waves. We expect stronger waves to produce higher mean flows. However, one can see in Fig. 3 that although one has the same number of maxima for the mean flow as for wave mean square surface deviation, the mean flow resonance frequencies are always a little smaller than those of wave mean square surface deviation.

Fig. 3
figure 3

Experimentally found resonance curves. Blue: mean square of surface displacement (3). Red: averaged flow through the channel

Full size image

3 Theoretical framework

3.1 Long wave integrated boundary layer model

Because the centrifugal and Coriolis forces are small with respect to gravity, we consider in our numerical investigation a straight channel with periodic boundary. The ratio of depth of the layer to horizontal wavelength is of the size \({{\tilde{h}}}_0/\tilde{L}\approx 0.01\) and a long wave approximation seems to be in order. With the non-dimensional variables (without tildes)

$$\begin{aligned} ({{\tilde{x}}},{{\tilde{z}}})={{\tilde{h}}}_0\,(x,z),\quad ({{\tilde{u}}},{{\tilde{w}}}) = {{\tilde{c}}}_0\,(u,w),\quad {{\tilde{t}}} = ({{\tilde{h}}}_0/{{\tilde{c}}}_0)\,t = \tau \,t,\quad {{\tilde{a}}} = a\,g, \end{aligned}$$

the Navier–Stokes eqs. in the accelerated frame of the channel reduce to

$$\begin{aligned} \partial _t u + \partial _x u^2 + \partial _z (uw) = \frac{1}{R_e}\partial _{zz}u - \partial _xh + a(t), \end{aligned}$$
(6)

where \(\partial _xh\) denotes the gradient of the hydrostatic pressure \(P=P_0+(h-z)\) and the surface tension effects are neglected. In (6), \(R_e={{\tilde{c}}}_0{{\tilde{h}}}_0/\nu\) is the Reynolds number and \({{\tilde{c}}}_0=\sqrt{g{{\tilde{h}}}_0}\) the shallow water wave velocity. The position of the free surface h(x, t) is determined by the kinematic boundary condition

$$\begin{aligned} \partial _t h = w_{z=h} - u_{z=h}\partial _x h. \end{aligned}$$
(7)

Let the ground be described by the function f(x). The boundary conditions for the velocity read

$$\begin{aligned} u=w=0 \text{ at } z=f(x),\quad \partial _zu = 0 \text{ at } z=h(x,t). \end{aligned}$$

According to (4), we introduce the flow rate

$$\begin{aligned} q(x,t) = \int _{f(x)}^{h(x,t)}dz\,u(x,z,t) \end{aligned}$$

and the local depth

$$\begin{aligned} H(x,t) = h(x,t) - f(x). \end{aligned}$$

Integrating (6) over z from f to h yields

$$\begin{aligned} \partial _t q + \partial _x\langle u^2\rangle _z= & {} -\frac{1}{R_e}\,\partial _zu|_{z=f} -H\partial _x(H+f) + H\,a(t) \end{aligned}$$
(8)
$$\begin{aligned} \partial _t H= & {} -\partial _x q , \end{aligned}$$
(9)

where \(\langle u^2\rangle _z= \int _f^hdz\,u^2\).

The two Eqs. (8,9) can be considered as an integrated boundary layer model (IBL), they are (1+1)-dimensional and will be discussed in the following. To close the system, we need an explicit profile u(z). Assuming a parabolic profile (thin film equation), one finds \(\partial _z u|_{z=f}=3q/H^2\) and \(\langle u^2\rangle _z=6q^2/(5\,H)\). Taking the values of the experiment, we have \(R_e\approx 3.5\cdot 10^4,\) which would lead to a rather long viscous dissipation time of \(R_e\tau /3\approx 1000\) s, much longer than that observed in the laboratory. A possibility to obtain a smaller effective Reynolds number is by changing the velocity profile to a boundary layer profile (Fig. 4)

$$\begin{aligned} u = \frac{q}{H}\,K\,\left( 1 - \frac{\cosh \beta (h-z)}{\cosh \beta H}\right) . \end{aligned}$$
(10)

The profile (10) is a solution of a viscous fluid on a laterally oscillating plane with \(1/\beta =\sqrt{2\nu /({{\tilde{\omega }}} {{\tilde{h}}}_0^2)}\) as the size of the boundary layer [11,12,13]. In our case, \(1/\beta \approx 0.02\), leading to an effective viscous damping enlarged by a factor 50. In addition, we compute \(K\approx 1\) from \(\int _f^h dz\,u=q\) and \(\partial _z u|_{z=f}=\beta q/H\), \(\langle u^2\rangle _z=q^2/H\).

Fig. 4
figure 4

Flow profiles. Blue: parabolic, red: boundary layer, \(\beta =50\), black: inviscid

Full size image

3.2 Numerical method

Assuming the profile (10), Eqs. (8,9) turn into

$$\begin{aligned} \partial _t q + \partial _x\left( \frac{q^2}{H}\right)= & {} -\frac{\beta }{R_e}\,\frac{q}{H} -H\partial _x(H+f) + H\,a(t) \end{aligned}$$
(11)
$$\begin{aligned} \partial _t H= & {} -\partial _x q. \end{aligned}$$
(12)

To integrate this set numerically, a semi-implicit pseudo-spectral method is established; for details see [14]. Due to the periodic lateral boundary conditions, fast Fourier transform of (11,12) can be applied and parts of the linear terms on the r.h.s. are treated at the time \(t+\delta t\), where \(\delta t\) is the time step. The scheme has the form

$$\begin{aligned} {\underline{M}} \cdot \left( \begin{array}{c} {\hat{q}}(k,t+\delta t)\\ {\hat{H}}(k,t+\delta t)\end{array}\right) = \left( \begin{array}{c} {\hat{Q}}(k,t)\\ {\hat{H}}(k,t)/\delta t \end{array}\right) , \end{aligned}$$
(13)

where \({\hat{q}}\), \({\hat{H}}\) are the spatial Fourier transforms of q, H, respectively, \({\hat{Q}}\) denotes the Fourier transform of

$$\begin{aligned} Q(x,t) = -\partial _x\left( \frac{q^2}{H}\right) - \frac{\beta }{R_e}\,\left( \frac{1}{H}-1\right)q -(H-1)\partial _xH - H\partial _x f + \frac{q}{\delta t} \end{aligned}$$
(14)

and the matrix \({\underline{M}}\) reads

$$\begin{aligned} {\underline{M}} = \left( \begin{array}{cc} \displaystyle \frac{1}{\delta t}+\frac{\beta }{R_e}, &{} ik-a(t) \\ ik, &{} \displaystyle \frac{1}{\delta t}\end{array}\right) . \end{aligned}$$
(15)

The derivatives in real space of (14) are approximated by finite differences. The semi-implicit method allows for a rather large time step \(\delta t=0.5 \cdot 10^{-4}\) and the code performs on small computers.

3.3 Results

The obstacle is modulated by the function

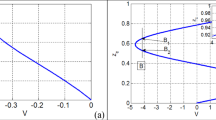
$$\begin{aligned} f(x) = \left\{ \begin{array}{cc}\displaystyle h_m\cos ^2\left( \frac{\pi }{\ell _m}(x-L/2)\right) , &{} L/2-\ell _m/2< x < L/2+\ell _m/2 \\ 0, &{} \text{ else } \end{array}\right. \end{aligned}$$

with \({{\tilde{h}}}_m=2\) cm and \({{\tilde{\ell }}}_m=0.6\) m, corresponding to a symmetric elevation of height \(h_m\) and length \(\ell _m\). The lateral excitation is chosen with (1). Figure 5 shows a frequency scan of the 5 cm depth liquid. The frequency runs from 0.03 Hz to 0.33 Hz in 100 steps, the driving amplitude \(a_0\) is adjusted according to (2).

Fig. 5
figure 5

Numerically found resonance curves from the IBL (8, 9). Blue: mean square of surface displacement measured opposite to the obstacle, similar to the experiment. Red: averaged flow through the channel for \(\alpha =-1/2\)

Full size image

A quite high agreement with our experiments concerning the mean square amplitude perturbations is achieved. At least a qualitative agreement is found for the flow rates. Note that the absolute values from Fig. 5 must be multiplied by the channels’ width (8.5 cm) to compare with those of Fig. 3. The absolute values of the flow rate, however not the positions of their maxima, depend sensitively on the damping rate \(\beta /R_e,\) which was chosen larger here by a factor 3 to ensure numerical stability. The maxima of the flow rates are always oriented left from those of the surface elevations, in agreement with the measurements. As expected, the flow rate changes sign for \(\alpha =1/2\) and vanishes for \(\alpha =0\).

The surface structures depend strongly on the driving frequency. They are pronounced best close to a resonance. Figure 6 shows space–time plots for three different \(\alpha\) just before the first strong resonance at \({{\tilde{f}}}=0.13\) Hz. Isolines of the surface function \({{\tilde{h}}}(x,t)=c\) are plotted for several c, where green colors correspond to \(c<{{\tilde{h}}}_0\) (troughs) and red to \(c>{{\tilde{h}}}_0\) (crests).

Fig. 6
figure 6

Space–time plots close to resonance \({{\tilde{f}}}=0.13\) Hz. For \(\alpha <0,\) mass is transported to the right side. Green: wave troughs, red: wave crests

Full size image

4 Conclusion

Wave resonances in terms of surface displacement and averaged mass flow generation have been investigated in an annular channel. The waves are generated by mechanical anharmonic periodic oscillations of the walls and the ground with given frequency f in the direction of the channel. An immersed mirror symmetric obstacle moves with the channel. In this way, periodic boundary conditions are realized in the experiment. We found that an averaged mass flow occurs if the symmetry \(a(t)=a(t_0-t)\) is violated.

Due to the fact that in the periodic channel not only transmission, but also reflection at the obstacle occur, resonances are expected at frequencies multiple of \({{\tilde{f}}}_r={{\tilde{c}}}_0/(2{{\tilde{L}}})\). As we have discussed in [9], odd multiples of \(f_0\) correspond to reflection modes, and even multiples appear only when transmission occurs. Both resonances emerge clearly in our experiment as well as in the numerical solutions based on a long wave model.

We found that the peak maxima of surface displacement and mass flow are slightly shifted for both experimental data and numerical results. The peak of the mean flow occurs always at a smaller frequency than that of the mean square displacement. This demonstrates that mass flow generation depends in a rather sophisticated way on the wave amplitude. Thereby, the (nonlinear) inertia terms play a fundamental role. For small Reynolds numbers, i.e., high viscosity and/or very thin layers, inertia can be neglected and our numerical solutions show neither resonances nor net mass flow for periodic oscillations, independently of the symmetry of the shape a(t) of the excitations.