1 Introduction

The full mathematical description of the dynamics of nonisothermal incompressible fluids is well known for a long time. The fluid velocity field is described by the Navier–Stokes equations, the temperature field is governed by the heat equation, and the location of the interface and its spatio-temporal evolution are determined by the kinematic boundary condition. All these equations are amended with suitable boundary conditions. As a result, a complex nonlinear dynamic boundary-value problem emerges and even nowadays, at the age of supercomputers, its further treatment, especially in three spatial dimensions, presents a great challenge.

On the other hand, a direct numerical solution of the set of governing equations mentioned above, may be considered merely as another experiment. To achieve a deeper insight into the physics behind pattern formation, other methods have been devised, for an overview, see [1]. Very often one of the three spatial dimensions is singled out due to the geometry of the system. A good example for this case provide thin viscous films on a solid substrate. Here, the behavior of the solutions in the vertical direction (z) is very different from that in the other two horizontal ones, and the 3D fields of dependent variables can be projected as a good approximation onto rather simple low-order polynomials in z. This approach is successfully applied in the long-wave theory, where upon this simplification, 2D thin-film equations describing 3D fluid flow in the system arise [2]. Normally in these theories, vertical velocities are small and inertia is neglected, referred to as the zero Reynolds number (Re) limit. A similar approximation for the heat equation (zero Péclet number (Pe) limit) results in a linear temperature profile and in a linear coupling between the local film thickness and the local temperature gradient. Using these approximations, both long-wave Marangoni and Rayleigh–Taylor instabilities as well as their combination were successfully described [3].

In the present paper, we shall develop a reduced description where the nonlinear terms in both the Navier–Stokes and the heat equation are kept, i.e., where Re and Pe are considered to be both non-zero. The reduction is accomplished by projection onto distinct 2nd-order polynomials that satisfy the boundary conditions exactly, in the tradition of the Galerkin method. This procedure is also known as the weighted-residual integral boundary layer (WRIBL) technique or the Karman–Pohlhausen method for both isothermal [4,5,6] and nonisothermal problems [7, 8]. It has been recently found that the Faraday instability can be described in this way also in its nonlinear regime [9, 10]. Projecting the temperature field onto polynomials, the method was then recently extended to the nonisothermal case [8] to study the impact of the Marangoni effect on the Rayleigh–Taylor instability.

It is a purpose of the present paper to show that the extended model with non-zero Pe is able to describe an oscillatory first instability in the case of a fluid located on the underside of a solid planar substrate stabilized by the Marangoni effect originating from heating at the gas side. This instability has a finite band of growing wave numbers that is bounded also from below away from zero, contrary to the monotonic long-wave instability found for \(Re=Pe=0\). The reduction to a low-dimensional system has the advantage that both the Hopf frequency and the critical Marangoni number can be derived analytically. A codimension-two point is determined where the oscillatory and the monotonic instabilities reverse their dominance. The results of the linearized reduced system are compared and checked with computations based on the linearized long-wave hydrodynamic basic equations and a good agreement is achieved. Finally, we present nonlinear simulations of the reduced system in 3D, showing persistent oscillating waves of the free surface over a long time terminated by rupture. To the best of our knowledge, this oscillatory instability was not reported before.

2 Derivation of the model

2.1 Governing equations

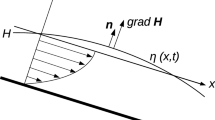
We consider a three-dimensional thin film of an incompressible fluid, see Fig. 1, with the deformable interface separating between the film and the ambient gas phase deposited on the underside of a horizontal, solid substrate in the gravity field g. The reference frame used in what follows is Cartesian with the x and y axes located in the plane of the substrate, whereas the z-axis is normal to the latter and points into the film. The location of the interface is a priori unknown and given by \(z=h(x,y,t)\).

In the long-wave approximation (LWA), the governing equations are written as [9]

$$\begin{aligned} Re\left[ \partial_t {\vec{\upsilon}}_H + \left( \vec{\upsilon}\cdot \nabla \right) \,\vec{\upsilon }_H\right]&= \partial _{zz} \vec{\upsilon }_H - \nabla _2 P \end{aligned}$$
(1a)
$$\begin{aligned} Pe\left[ \partial _t T + \left( \vec{\upsilon }\cdot \nabla \right) \, T \right]&= \partial _{zz} T \ . \end{aligned}$$
(1b)

Here, \(\vec{\upsilon }_H =(v_x,v_y)\) denotes the horizontal component of the velocity field vector \(\vec{\upsilon }\), T is the temperature field, the subscripts to \(\partial\) denote the variables with respect to which partial differentiation is taken, and \(\nabla _2=(\partial _x,\partial _y)\). All variables were made dimensionless by applying the following scaling:

$$\begin{aligned} {\vec{t}}= & {} \tau \,t,\quad ({\tilde{x}},{\tilde{y}},{\tilde{z}}) = d\,(x,y,z),\\ {\tilde{P}}= & {} \frac{\nu ^2\rho }{d^2}\, P,\quad \widetilde{\vec {\upsilon }} = U_0\, \vec {\upsilon }, \quad {\tilde{T}} = {\tilde{T}}_e + \Delta {\tilde{T}}\,T \end{aligned}$$

where \(\tau = d/U_0\), \(U_0\) stands for a certain characteristic velocity, d for the mean depth of the film, and \({\tilde{T}}_e\) is the constant environment temperature (variables with tilde bear a dimension). The temperature difference

$$\begin{aligned} \Delta {\tilde{T}} ={\tilde{T}}_0 - {\tilde{T}}_e < 0 \end{aligned}$$
(2)

represents the difference between the uniformly cooled substrate and the warmer environment. Reynolds and Péclet numbers are defined via

$$\begin{aligned} Re = \frac{U_0 d}{\nu },\quad Pe=Re\,Pr \end{aligned}$$

with the Prandtl number

$$\begin{aligned} \quad Pr = \frac{\nu }{\kappa }. \end{aligned}$$
(3)
Fig. 1
figure 1

A sketch of the problem. A thin film of an incompressible fluid of density \(\rho\), kinematic viscosity \(\nu\) and thermal diffusivity \(\kappa\) is placed on the underside of a solid and uniformly cooled horizontal planar substrate with the temperature \({\tilde{T}}_0\) with respect to the ambient

Full size image

2.2 Boundary conditions

In LWA, the boundary conditions for the velocity field are

$$\begin{aligned} \vec{\upsilon }_H = 0\quad \text{ at }\ z=0,\qquad \partial _z\vec{\upsilon }_H = -M\!a\nabla _2\theta \quad \text{ at }\ z=h. \ \end{aligned}$$
(4)

Here, we have introduced the new 2D variable

$$\begin{aligned} \theta (x,y)=T(x,y,z=h) \end{aligned}$$
(5)

as the temperature along the free surface. The Marangoni number \(M\!a\) is defined as

$$\begin{aligned} M\!a= \frac{\gamma _T\Delta {\tilde{T}}}{\rho \nu U_0} \end{aligned}$$
(6)

where \(\gamma _T=-d\sigma /dT\) and \(\sigma\) is the surface tension between the liquid and the ambient gas. In what follows, the Marangoni number \(Ma\) is negative.

For the temperature, we find

$$\begin{aligned} T = 1\quad \text{ at }\ z=0,\qquad \partial _z T = -B\,\theta \quad \text{ at }\ z=h \end{aligned}$$
(7)

with the Biot number B

$$\begin{aligned} B=\frac{qd}{\alpha } \end{aligned}$$
(8)

where q is the rate of heat transfer from the liquid to the ambient gas at the interface and \(\alpha\) is the thermal conductivity of the liquid.

The location of the free surface is determined by the kinematic boundary condition

$$\begin{aligned} \partial _t h = v_z - \vec{v}_H\cdot \nabla _2\,h \end{aligned}$$
(9)

at \(z=h\). Note that in convection problems, the Marangoni number is sometimes defined as \(M=M\!a\,Pe\,B/(1+B)\).

2.3 Hydrostatic pressure

In LWA, the pressure consists of components, namely, the hydrostatic and the capillary ones [9], so its gradient reads

$$\begin{aligned} \nabla _2 P(x,y) = G\,\nabla _2 h - \Gamma \nabla _2\nabla _2^2\, h \end{aligned}$$
(10)

with the dimensionless groups Galileo and inverse Crispation number

$$\begin{aligned} G = -\frac{gd^2}{\nu U_0} <0,\qquad \Gamma = \frac{\sigma }{\rho \nu U_0}, \end{aligned}$$
(11)

respectively.

Thus, the six groups

$$\begin{aligned} Re,\ G,\ \Gamma ,\ M\!a,\ Pe,\ B \end{aligned}$$

define our problem. Since \(U_0\) can be chosen arbitrarily, one of the first five parameters can be put to one, in what follows we shall use viscous scaling \(U_0=\nu /d\), leading to \(Re=1\) and \(Pe=Pr\). g.

2.4 Polynomials and 2D variables

In addition to the surface temperature (5), we introduce next the 2D vector field

$$\begin{aligned} {\vec{q}}(x,y,t) = \int _0^{h(x,y,t)} dz\,{\vec {\upsilon }}_H(x,y,z,t) \end{aligned}$$
(12)

which represents the horizontal flow rate. We now use the following representation for the horizontal velocity field

$$\begin{aligned} \vec {\upsilon }_H(x,y,z,t)= & {} g_1(z;h)\,{\vec{q}}(x,y,t) \nonumber \\{} & {} - M\!a\, g_2(z;h)\,\nabla _2\theta (x,y,t) \end{aligned}$$
(13)

with the polynomials

$$\begin{aligned} g_1 = 3\frac{zh-z^2/2}{h^3},\qquad g_2 = -\frac{zh-3z^2/2}{2h}. \end{aligned}$$
(14)

Note that

$$\begin{aligned} \int _0^h dz\,g_1 = 1,\qquad \int _0^h dz\,g_2 = 0, \end{aligned}$$

and for \(z=h\)

$$\begin{aligned} \qquad \partial _z g_1= 0, \qquad \partial _zg_2 = 1. \end{aligned}$$

Thus, the representation (13) satisfies the boundary conditions (4) for arbitrary \({\vec{q}}\) and \(\theta\). For the temperature, we take also a quadratic dependence on z and write

$$\begin{aligned} T(x,y,z,t)= & {} g_3^2(z;h)\left( 1-\theta (x,y,t)\right) \nonumber \\{} & {} +\left( 1+Bzg_3(z;h)\right) \,\theta (x,y,t) \end{aligned}$$
(15)

with

$$\begin{aligned} g_3 = 1-\frac{z}{h}. \ \end{aligned}$$
(16)

Since \(g_3(0)=1,\ g_3(h)=0\) and \(\partial _z(zg_3)=-1\) at \(z=h\), the representation (15) fulfills (5) and the boundary conditions (7) for arbitrary \(\theta\). The boundary condition (9) can be reformulated with (12) as

$$\begin{aligned} \partial _t h = -\nabla _2\cdot {\vec{q}}. \end{aligned}$$
(17)

2.5 The dimension-reduced model

To derive a set of evolution equations for \(h,{\vec{q}}\) and \(\theta\), we insert Eqs. (13,15) into Eqs. (1a,1b), multiply Eqs. (1a) and (1b) by the weight functions \(W_1(z;\!h)\) and \(W_2(z;\!h)\), respectively, and integrate them over \(0 \le z \le h\). After some algebra, a set of 2D evolution equations is obtained with the numerical values of the coefficients depending on the choice of \(W_i\). Choosing

$$\begin{aligned} W_1 = g_1,\qquad W_2 = 1 \end{aligned}$$

we obtain the following set complemented by Eq. (17):

$$\begin{aligned}&\frac{6}{5}\,Re\left( \partial _t{\vec{q}} + \frac{9}{7}\,\nabla _2\cdot \left( \frac{{\vec{q}}\otimes {\vec{q}}}{h}\right) -\frac{1}{7}\frac{{\vec{q}}\,\nabla _2\cdot {\vec{q}}}{h}\right) \nonumber \\&=\ -\frac{3}{h^2}\,{\vec{q}} + h\nabla _2\left( \Gamma \nabla _2^2\,h - G\,h\right)-\frac{3}{2}\,M\!a\nabla _2\theta, \end{aligned}$$
(18a)
$$\begin{aligned}&\frac{(Bh+4)}{6}\,\partial _t\theta + \frac{2}{15}\,\frac{(\nabla _2\cdot {\vec{q}})\,(\theta -1)}{h}\nonumber \\&-\frac{19B}{120}\,\theta \,\nabla _2\cdot {\vec{q}}\nonumber \\&+ \frac{7B}{40}\,\frac{\theta \,{\vec{q}}\cdot \nabla _2h}{h} +\frac{7Bh+32}{40h}\,{\vec{q}}\cdot \nabla _2\theta \nonumber \\&= \ -\frac{2}{Pe}\,\frac{Bh\theta +\theta -1}{h^2}, \end{aligned}$$
(18b)
$$\begin{aligned}&\partial _t h =\ -\nabla _2\cdot {\vec{q}}. \ \end{aligned}$$
(18c)

Following the LWA, only first-order terms in the derivatives are included in the left-hand sides of Eqs. (18).

For \(B\ll 1\), Eq. (18b) takes a much simpler form

$$\begin{aligned}{} & {} \frac{2}{3}\,\partial _t\theta + \frac{2}{15}\,\frac{(\nabla _2\cdot {\vec{q}})\,(\theta -1)}{h} +\frac{4}{5}\,\frac{{\vec{q}}\cdot \nabla _2\theta }{h} \nonumber \\{} & {} \quad = -\frac{2}{Pe}\,\frac{Bh\theta +\theta -1}{h^2}, \end{aligned}$$
(19)

which can be compared directly to the expansions given by Trevelyan et al. [11] and Sterman-Cohen and Oron [8]. As mentioned above, the coefficients depend on the choice of the weight function \(W_2\) and are slightly different in all the three works. Taking, for instance, \(W_2=z\), we find for the case \(B\ll 1\)

$$\begin{aligned}{} & {} \frac{5}{6}\,\partial _t\theta + \frac{1}{10}\,\frac{(\nabla _2\cdot {\vec{q}})\,(\theta -1)}{h} +\frac{11}{10}\,\frac{{\vec{q}}\cdot \nabla _2\theta }{h}\nonumber \\{} & {} \quad = -\frac{2}{Pe}\,\frac{Bh\theta +\theta -1}{h^2}. \end{aligned}$$
(20)

Note that in both limits Eqs. (19) and (20), we retain B in the right-hand side of the equations. Then it is possible to approximate the solution if the convective terms are absent in the heat equation what formally corresponds to \(\kappa \rightarrow \infty\) or \(Pe\rightarrow 0\) with the well-known result, e.g., [2, 8]

$$\begin{aligned} \theta = \frac{1}{1+Bh}. \end{aligned}$$

3 Linear stability analysis

It is easy to identify the base state for Eqs. (18) in the form of the quiescent conductive state with a flat interface that reads

$$\begin{aligned} {\vec{q}}_0 = 0,\quad h_0 = 1,\quad \theta _0 = \frac{1}{1+B}. \ \end{aligned}$$
(21)

Due to isotropy of the laterally unbounded system in the x-y plane, the linear analysis may be performed in just one horizontal spatial dimension, say x. Substituting

$$\begin{aligned}& h=h_0+ik\eta \exp (ikx+\lambda t),\\&\theta =\theta _0 + ik\vartheta \exp (ikx+\lambda t),\\& q_x = q \exp (ikx+\lambda t) \end{aligned}$$

into Eq. (18), results after linearization in the real-valued linear set of algebraic equations

$$\begin{aligned}&Re\,\lambda \, q = \frac{5}{6}\left( -3\,q + k^2(G+\Gamma k^2)\,\eta + \frac{3}{2} k^2M\!a\,\vartheta \right), \end{aligned}$$
(22a)
$$\begin{aligned}&Pe\left( \lambda \vartheta -\frac{7}{16}\,B\,q\right) = -3\,(\vartheta + B\eta ) \end{aligned}$$
(22b)
$$\begin{aligned}&\lambda \eta = -q. \end{aligned}$$
(22c)

For the sake of simplicity, we assume in this section from here on a physically relevant case of a small Biot number \(B\ll 1\), according to the limits of Eq. (19). The solvability condition for Eqs. (22) represents a cubic polynomial equation

$$\begin{aligned} Re\,\lambda ^3 + a_2\,\lambda ^2 + a_1\,\lambda + a_0 = 0 \end{aligned}$$
(23)

with

$$\begin{aligned} a_0&= \frac{5k^2}{2Pe}\left( G+\Gamma k^2- \frac{3}{2}\,B\, M\!a\right), \end{aligned}$$
(24a)
$$\begin{aligned} a_1&= \frac{15}{2Pe} + \frac{5}{6} k^2(G+\Gamma k^2) -\frac{35}{64}\,B\,M\!a\,k^2,\\ \end{aligned}\\$$
(24b)
$$\begin{aligned} a_2&= \frac{5}{2} + \frac{3Re}{Pe}. \ \end{aligned}$$
(24c)

At the threshold of a monotonic instability \(\lambda =0\), leading thus to \(a_0=0\), and the system is monotonically unstable if \(a_0<0\), leading to

$$\begin{aligned} B\,M\!a> B\,M\!a_c^M = \frac{2}{3}\,\left( G + \Gamma k^2\right) . \ \end{aligned}$$
(25)

Equation (25) yields the threshold of the monotonic instability as

$$\begin{aligned} BM\!a_{c,min}^M=\frac{2G}{3} \end{aligned}$$
(26)

taking place at \(k=0\). For Marangoni numbers larger than \(M\!a_{c.min}^M\) the stabilizing Marangoni effect becomes too small, and the Rayleigh–Taylor instability emerges. This is the well-known condition for the long-wave Marangoni instability in a thin film that is not affected by inertia and thermal convection (\(Re=Pe=0\)).

For the onset of an oscillatory (Hopf) instability, \(\lambda =i\omega _c\) with a real \(\omega _c\), we obtain \(\omega _c =\sqrt{a_0/a_2}\) and, since \(a_2>0\), one must have \(a_0>0\). The latter is possible for \(M\!a<M\!a_c^M\), i.e. where the monotonic instability does not emerge, and, therefore, occurs then as a first instability increasing \(M\!a\) if Pe exceeds a certain critical value. The critical Marangoni number \(M\!a_c^{os}\) for the Hopf instability is found from Eq. (23) equating \(a_0\,Re = a_1 a_2,\ \omega _c^2 = a_0/a_2\) and turns out as

$$\begin{aligned} B \,M\!a> B\, M_c^{os}&= \frac{1}{\frac{35}{32}-\frac{27Re}{16Pe}} \left( \frac{15+\frac{18Re}{Pe}}{Pe\, k^2} + \frac{5}{3}(G+\Gamma k^2)\right) , \end{aligned}$$
(27a)
$$\begin{aligned} \omega _c^2&= \frac{5}{2}\,k^2\,\frac{2(G+\Gamma k^2)-3B\,M\!a}{5Pe + 6Re} \ > \ 0. \ \end{aligned}$$
(27b)
Fig. 2
figure 2

Left: variation of the critical \(BM_c^{os}\) with k based on Eq. (27a) for the fluid parameters \(\nu = 5\cdot 10^{-6}\text{ m}^2/\text{s },\ \rho = 920\, \text{ kg }/\text{m}^3,\ \sigma = 0.019\, \text{ N/m },\ d = 0.5\,\text{ mm },\ B=0.1, \ Re=1\) and different Prandtl (Péclet) numbers. The black solid line denotes the onset of the monotonic instability (\(a_0=0\) in Eq. (24)). Above the solid line, \(\omega _c^2<0\) in Eq. (27b) and, therefore, the dashed part of the lines are fictitious. Right: the same for the basic hydrodynamic equations in LWA

Full size image

The critical value \(M_c^{os}\) is a convex function of k and has a minimum at (Fig. 2)

$$\begin{aligned} k_c^{os} = \left[ \frac{9}{\Gamma Pe}\left( 1+\frac{6Re}{5Pe}\right) \right] ^{1/4}. \ \end{aligned}$$
(28)

Assuming \(\displaystyle Re/Pe = 1/Pr \ll 1\), which may materialize via either \(Pe \gg 1\) or \(Re \ll 1\), both equivalent to \(Pr \gg 1\), we find that at the lowest order of 1/Pe or for \(Re=0\), respectively, the minimal value of \(M\!a_c^{os}\) is

$$\begin{aligned} B M_{\tiny \text{ c,min }}^{os} = \frac{32}{7}\left( 2\sqrt{\frac{\Gamma }{Pe}}+\frac{1}{3} G\right) . \end{aligned}$$
(29)

If this value becomes lower than the monotonic instability threshold \(B M\!a_c^M\) given by Eq. (25), an oscillatory instability sets in first with a finite wave number given by Eq. (28) if \(M\!a\) reaches the value \(M^{os}_{\tiny \text{ c,min }}\), see Fig. 2. For \(Pe\rightarrow \infty\), one finds

$$\begin{aligned} B M_{\tiny \text{ c,min }}^{os} = \frac{32}{21} G, \ \end{aligned}$$
(30)

which is always smaller than the expression in Eq. (25), since G is negative. However for this case, \(k_c\rightarrow 0\) and the wave length of the critical modes would become very long and the Hopf frequency (27b) tends to zero.

A codimension-two point where both types of instability set in at the same value of the Marangoni number is found from \(M^M_c=M^{os}_{\tiny \text{ c,min }}\) and yields the condition

$$\begin{aligned} Pe^{CD2} = \frac{1024}{9}\,\frac{\Gamma }{G^2}. \end{aligned}$$
(31)

For \(Pe > Pe^{CD2}\), the instability of the motionless state is oscillatory.

It is interesting to note that qualitatively similar results Eqs. (27–30) can be derived if inertia is neglected, i.e., \(Re\ll 1\), at least for not too small Pe. In the case of \(Re=0\), the eigenvalue problem (22) reduces to a second-order problem, which is easily solved and the critical thresholds for both monotonic and oscillatory instabilities are obtained by the same equations (26-29), but now with \(Re=0\). This is probably due to the fact that the fluid velocities for this case stay rather small and inertia effects play no significant role.

To demonstrate that our results are not an artifact of the projection method used to obtain the set of Eqs. (18), we next solve the linearized long-wave set of Navier–Stokes and heat equations (1) by a standard finite-difference method for the same parameters and found a phase diagram presented in the right frame of Fig. 2. It clearly shows that for \(Pe=25\), the first instability of the quiescent state is oscillatory.

4 Numerical results

Finally, we present our numerical results based on the reduced system (18). An FTCS (forward-time central-space) [12] finite-difference method has been applied with a fixed time step \(\Delta t=0.5\cdot 10^{-3}\) and grid spacing \(\Delta x=1\). The resolution is fixed with 300 x 300 points and the lateral boundaries are periodic. For all runs, random initial conditions for the interface are used

$$\begin{aligned} {\vec{q}}=0,\quad h = 1 + 0.1\,\xi ,\quad \theta = 1/(1+B\,h) \end{aligned}$$

with \(\xi\) as equally distributed random numbers in \([-0.5,0.5]\). The fluid parameters used are given in the caption of Fig. 2 and \(Pe=Pr=25\) allow for the emergence of an oscillatory instability at \(M\!a\approx -440\), whereas the monotonic instability sets in at \(M\!a\approx -400\). Note that here \(B=0.1\).

Fig. 3
figure 3

Left: contour lines of the surface profile in the monotonic regime \(M\!a=-300\), just before film rupture. Right: contour lines of the surface profile in the oscillatory regime \(M\!a=-400\). An oscillating wave occurs with the frequency and the wave length in good fit with the linear theory, compare Fig. 2. At a longer time, the film also ruptures

Full size image

For \(M\!a=-300\), we are clearly in the monotonic region of Fig. 2 and after a certain time of coarsening, a few single stalactites survive and the code diverges, as a probable sign of film rupture, see Fig. 3, left frame.

The situation is completely different in the oscillatory regime for \(M\!a= -400\), Fig. 3, right frame. Now, the amplitudes of the emerging pattern remain small for a long time before more or less suddenly film rupture takes place, see Fig. 4. During this phase, the film surface has the form of mixed traveling and standing waves, nonlinear selection processes do not take place probably due to the rather small amplitudes. The emergence of the Hopf bifurcation is obvious from very early stages of the evolution.

Fig. 4
figure 4

Variation of the maximal and minimal values of h(x, y, t) with time. Rupture occurs after \(t\approx 155\) s. Thickness h is presented in units of the mean film thickness, whereas time t is shown in seconds. \(Ma=-400,\, B=0.1,\,Pe=Pr=25\)

Full size image

5 Conclusions

Fig. 5
figure 5

Viscosity at the codimension-two point for \(\sigma =0.02\) N/m, \(\kappa =0.15\cdot 10^{-6}\) \(\hbox {m}^2\)/s, \(\rho =920\) kg/\(\hbox {m}^3\). The x marks the values used for the present study

Full size image

We have shown that an oscillatory (wave) instability emerges via the Marangoni effect for a Rayleigh–Taylor unstable thin layer heated from the gas side. Increasing the (negative) Marangoni number, this instability may bifurcate first from the motionless flat film state for a certain range of fluid parameters and mean layer depth. For rather thin films and/or high fluid viscosity, this instability is obliterated by the monotonic long-wave instability. Inspection of the codimension-two condition (31) yields an upper bound for the kinematic viscosity of the liquid

$$\begin{aligned} \nu < \frac{9}{1024}\,\frac{\rho g^2 d^5}{\sigma \kappa } \end{aligned}$$

which enables the emergence of the oscillatory instability. It is presented for a typical set of fluid parameters \(\sigma =0.02\) N/m, \(\kappa =0.15\cdot 10^{-6}\) \(\hbox {m}^2\)/s, \(\rho =920\) kg/\(\hbox {m}^3\) as a function of the mean depth in Fig. 5. It demonstrates that the layer must be rather thick to exhibit an oscillatory instability with an increase in the kinematic viscosity of the fluid. A similar instability behavior has been found based on the original hydrodynamic equations which justifies the projection method developed here. Nonlinear simulations of the set of reduced model equations terminate always with rupture (or dripping of some singular stalactites) in both the oscillatory and the monotonic flow regimes, probably due to the rather large mean film thickness of 0.5 mm used for our computations.

Finally, the physical situation described in this paper in which the dynamics of a Rayleigh–Taylor unstable thin liquid film is heated at the gas side has been studied both theoretically and experimentally. In the limit of the inertialess long-wave theory, heating the film at its interface provides an extra-stabilization mechanism along with the surface tension which leads to the emergence of the monotonic instability and its subsequent saturation [13, 14] in both 2D and 3D. The same was found experimentally in double-layered systems [15] and then reproduced theoretically [3].

The emergence of the oscillatory instability in this physical setting has been found for the first time, and a possibility of its saturation, which was not found here, may be explored in more detail in the future.