Dynamic and wave propagation analysis of periodic smart beams coupled with resonant shunt circuits: passive property modulation

Abstract

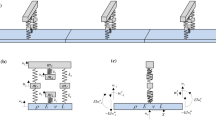
The present study deals with analyzing the dynamic behavior of a smart beam coupled with piezoelectric materials in the unimorph and bimorph configurations connected to resonant shunt circuits. The resonant shunt circuit connection is applied to promote and passively modulate the vibration and flexural wave propagation attenuation. A Spectral Element Method (SEM)-based approach for the periodic smart structure is developed that is capable of efficiently analyzing various configurations of periodicity and piezoelectric attachments in a generic framework. The wave attenuation is obtained based on the Transfer Matrix Method (TMM). Numerical analyses reveal that the effective wavenumber presents local attenuation behavior at the same frequencies of the vibration as per the shunt design, indicating the shunt circuit’s impedance associated with tuned frequency. The internal resonance characteristics of the resonant shunt circuits and their effects on the beam response are investigated in detail. The proposed periodic smart beam system along with the spectral element approach for analyzing the dynamics and wave propagation behavior of such systems, lays out further potential avenues for designing more complex configurations of smart structures and multifunctional metamaterials.

A Transfer matrix method

Transfer matrix method allows us to exploit the dynamic stiffness matrix of a single piezo-beam for analyzing periodic arrangements of such beams. The spectral transfer matrix method [32] is an analytical spectral approach of the system in the state-space form to directly obtain the transfer matrix of the structure. From dynamic system relationship, a frequency-domain state-vector equation is obtained as

$$\begin{aligned} \frac{d\hat{{\mathbf {y}}}(x)}{\mathrm{d}x}={\mathbf {A}}\left( \omega \right) \hat{{\mathbf {y}}}(x) \qquad \left( 0\le x\le L\right) , \end{aligned}$$

(40)

where ${\mathbf {A}}\left( \mathbf {\omega }\right)$ is the system coefficient matrix with $[2n \times 2n]$ degrees of freedom, and $\hat{{\mathbf {y}}}(x)=\{\hat{{\mathbf {d}}}\ \ \ \hat{{\mathbf {F}}}\}^{\mathbf {T}}$ is the state vector with $\hat{{\mathbf {d}}}$ as the spectral nodal displacements and $\hat{{\mathbf {F}}}$ the spectral nodal forces vectors. The general solution of Eq. (40) for a structural element of length L is given by

$$\begin{aligned} \hat{{\mathbf {y}}}\left( L\right) ={\mathbf {e}}^{{\mathbf {A}}L}\hat{{\mathbf {y}}}\left( {\mathbf {0}}\right) ={\mathbf {T}}\left( \mathbf {\omega }\right) \hat{{\mathbf {y}}}\left( {\mathbf {0}}\right) , \end{aligned}$$

(41)

where ${\mathbf {T}}\left( \mathbf {\omega }\right) ={\mathbf {e}}^{{\mathbf {A}}L}$ is the transfer matrix, in its exponential form. If all eigenvectors of the matrix ${\mathbf {A}}$ are linearly independent, the transfer matrix can be written as

$$\begin{aligned}&\left\{ \begin{matrix}u_{r}\\ {-F}_{r}\\ \end{matrix}\right\} =\left[ \begin{matrix}-S_{lr}^{-{\mathbf {1}}}S_{ll}&{}-S_{lr}^{-{\mathbf {1}}}\\ S_{rl}-S_{rr}S_{lr}^{-{\mathbf {1}}}S_{ll}&{}{-S}_{rr}S_{lr}^{-{\mathbf {1}}}\\ \end{matrix}\right] \left\{ \begin{matrix}u_{l}\\ F_{l}\\ \end{matrix}\right\} \nonumber \\&\quad or\ \ \ \ \ \ \ \ \ {\mathbf {q}}_{r}={\mathbf {T}}(\omega ){\mathbf {q}}_{l}, \end{aligned}$$

(42)

where ${\mathbf {T}}\left( \mathbf {\omega }\right)$ relates the left (l) state vector ${\mathbf {q}}_l$ with the right (r) state vector ${\mathbf {q}}_r$ of the unit-cell [46]

$$\begin{aligned} {\mathbf {T}}\left\{ \begin{matrix}{u}_{l}\\ {F}_{l}\\ \end{matrix}\right\} \ =\ {e}^{\mu }\ \ \left\{ \begin{matrix}{u}_{r}\\ {F}_{r}\\ \end{matrix}\right\} \ \ \ \ \ \ or \ \ {{\mathbf {T}}}{{\mathbf {q}}}=\ {e}^{\mu }{\mathbf {q}}, \end{aligned}$$

(43)

${\mathbf {A}}=e^\mu$ is the corresponding eigenvector matrix and ${\mathbf {q}}$ are the corresponding eigenvectors derived from the Bloch wave eigenproblem with $\mu$ being the eigenvalues.