Influences of inherent geometrical nonlinearity of high-static-low-dynamic-stiffness resonator on flexural wave attenuation performance of metamaterial beam

Abstract

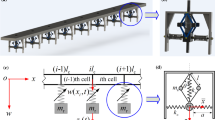
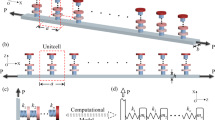
Metamaterials with high-static-low-dynamic stiffness (HSLDS) resonators possess the ability in low/ultra-low frequency flexural wave attenuation. However, the inherent geometrical nonlinearity of the HSLDS resonators was used to be neglected for simplicity, leading to severe restriction of its operating range. In this paper, the intrinsic geometric nonlinearity of the HSLDS resonator is considered to extend its applications. The nonlinear dynamic model of a metamaterial beam coupled with nonlinear HSLDS resonators is established based on the Galerkin method. An efficient frequency-domain analysis strategy, which consists of the harmonic balance method (HBM), arc-length continuation, and Hill’s method, is then adopted to compute periodic solution branches. Results show that once the excitation amplitude reaches some extent and the nonlinear stiffness of the resonator plays a dominant role due to higher response, only the nonlinear model can capture the dynamics of the coupling system. Furthermore, in the case of large responses, double peaks in frequency response bend right, and the second peak is significantly suppressed. Meanwhile, the location and wave attenuation performance of the bandgap remains unchanged. The results indicate that the nonlinear metamaterial beam performs better in the range out of bandgap. Hence, the nonlinear metamaterial is more robust against mistuning. Due to the above merit, the operating range of HSLDS resonators and the bearable excitation amplitude in nonlinear metamaterial beam are enhanced four times compared to linear metamaterial beam. Thus, the metamaterial beam with nonlinear HSLDS resonators has better environmental adaptability and broader application prospects.

Appendix

1.1 Harmonic balance method

Introduce the derivative operator:

$$ \nabla = {\text{diag}}(0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla_{1} , \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla_{j} , \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla_{H} ){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{with}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla_{j} = j\left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 1} & 0 \\ \end{array} } \right] $$

(A1)

The velocity and acceleration can be expressed by Fourier coefficient vectors, which are given by Eq. (17):

$$ \begin{gathered} \dot{x}(t) = \omega ({\varvec{T}}(\omega t) \otimes {\varvec{I}}_{n} )(\nabla \otimes {\varvec{I}}_{n} ){\varvec{X}} = \omega [({\varvec{T}}(\omega t)\nabla ) \otimes {\varvec{I}}_{n} ]{\varvec{X}} \hfill \\ \ddot{x}(t) = \omega^{2} ({\varvec{T}}(\omega t) \otimes {\varvec{I}}_{n} )(\nabla^{2} \otimes {\varvec{I}}_{n} ){\varvec{X}} = \omega^{2} [({\varvec{T}}(\omega t)\nabla^{2} ) \otimes {\varvec{I}}_{n} ]{\varvec{X}} \hfill \\ \end{gathered} $$

(A2)

Substituting Eq. (16), Eq. (A1) and Eq. (A2) into Eq. (15), and balancing the harmonic terms by utilizing the orthogonality property of trigonometric basis, the nonlinear system Eq. (15) of differential equations in the time domain is transformed into nonlinear algebraic equations in the frequency domain:

$$ {\varvec{R}}({\varvec{X}},\omega ) = {\varvec{Z}}(\omega ){\varvec{X}} + {\varvec{F}}_{nl} ({\varvec{X}}) - {\varvec{P}} = {\mathbf{0}} $$

(A3)

where ${\varvec{Z}}(\omega )$ is the dynamic stiffness matrix, which is block-diagonal:

$$ \begin{gathered} {\varvec{Z}}(\omega ) = \omega^{2} \nabla^{2} \otimes {\varvec{M}} + \omega \nabla \otimes {\varvec{C}} + {\varvec{I}}_{2H + 1} \otimes {\varvec{K}} = {\text{diag}}({\varvec{K}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{Z}}_{1} , \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{Z}}_{j} , \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{Z}}_{H} ) \hfill \\ {\varvec{Z}}_{j} = \left[ {\begin{array}{*{20}c} {{\varvec{K}} - j^{2} \omega^{2} {\varvec{M}}} & {\omega {\varvec{C}}} \\ { - \omega {\varvec{C}}} & {{\varvec{K}} - j^{2} \omega^{2} {\varvec{M}}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(A4)

With the above derivation of equations of motion, the problem is converted into finding the Fourier coefficients of Eq. (15), which can be accomplished by the New-Raphson procedure. Note that the nonlinear term ${\varvec{f}}_{nl}$ and ${\varvec{F}}_{nl}$ cannot be directly computed in the frequency domain. The alternating frequency-time(AFT) scheme [42], which computes the nonlinear term in the time domain and then switches back to the frequency domain, is coupled with standard HBM.

1.2 Tangent prediction

With the calculated solution point $({\varvec{X}}_{i} ;\omega_{i} )$ on the hand, the predicted point $(\overline{\user2{X}}_{i + 1} ;\overline{\omega }_{i + 1} )$ can be obtained using the first-order Taylor expansion of Eq. (15) at point $({\varvec{X}}_{i} ;\omega_{i} )$. After neglecting high-order terms and introducing a constrain equation, a tangent vector ${\varvec{t}} = (\Delta {\varvec{X}};\Delta \omega )$ can be obtained from

$$ \left[ {\begin{array}{*{20}c} {\left. {{\varvec{R}}_{{\varvec{X}}} } \right|_{{({\varvec{X}}_{i + 1} ;\omega_{i + 1} )}} } & {\left. {{\varvec{R}}_{\omega } } \right|_{{({\varvec{X}}_{i + 1} ;\omega_{i + 1} )}} } \\ {{\varvec{t}}_{i - 1}^{T} } & {} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta {\varvec{X}}_{i} } \\ {\Delta \omega_{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ 1 \\ \end{array} } \right] $$

(A5)

where ${\varvec{R}}_{{\varvec{X}}} = {{\partial {\varvec{R}}} \mathord{\left/ {\vphantom {{\partial {\varvec{R}}} {\partial {\varvec{X}}}}} \right. \kern-0pt} {\partial {\varvec{X}}}}$ is the Jacobian matrix and is given by:

$$ \begin{gathered} {\varvec{R}}_{\omega } = {\varvec{Z}}_{\omega } {\varvec{X}} \hfill \\ \;{\varvec{Z}}_{\omega } = \frac{{\partial {\varvec{Z}}}}{\partial \omega } = 2\omega \nabla^{2} \otimes {\varvec{M}} + \nabla \otimes {\varvec{C}} \hfill \\ \end{gathered} $$

(A6)

Then, a normalization condition is added to unify the tangent vector with respect to the parameter $\omega$:

$$ {\varvec{t}}_{i} = \left[ {\frac{{\Delta {\varvec{X}}_{i} }}{{\left| {\Delta \omega_{i} } \right|}};\frac{{\Delta \omega_{i} }}{{\left| {\Delta \omega_{i} } \right|}}} \right] $$

(A7)

Eventually, the predicted point can be given at a distance $\Delta s_{i}$ along the direction ${\varvec{t}}_{i}$:

$$ \left[ {\begin{array}{*{20}c} {\overline{\user2{X}}_{i + 1} } \\ {\overline{\omega }_{i + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{X}}_{i} } \\ {\omega_{i} } \\ \end{array} } \right] + \Delta s_{i} {\varvec{t}}_{i} $$

(A8)

where $\Delta s_{i}$ represents the arc length of $i - {\text{th}}$ solution point. Note that a step control decides whether a continuation algorithm works well, affecting the continuation’s correctness and robustness. In Wu’s study [40], an improved adaptive method for arc-length control is proposed and adopted in our work.

1.3 Orthogonal corrections

In general, the predicted point is not a solution of Eq. (15), and the next solution point can be then computed by using the New-Raphson algorithm iteratively in the direction orthogonal to tangent ${\varvec{t}}$ until the criteria $\left\| {{\varvec{R}}_{i + 1}^{k} } \right\| \le \varepsilon$ satisfies, where $\varepsilon$ is a user-defined convergence criterion.

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {\left. {{\varvec{R}}_{{\varvec{X}}} } \right|_{{({\varvec{X}}_{i + 1}^{k} ;\omega_{i + 1}^{k} )}} } & {\left. {{\varvec{R}}_{\omega } } \right|_{{(\;{\varvec{X}}_{i + 1}^{k} ;\omega_{i + 1}^{k} )}} } \\ {{\varvec{t}}_{i}^{T} } & {} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\delta {\varvec{X}}_{i + 1}^{k + 1} } \\ {\delta \omega_{i + 1}^{k + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - {\varvec{R}}_{i + 1}^{k} } \\ 0 \\ \end{array} } \right] \hfill \\ \left[ {\begin{array}{*{20}c} {{\varvec{X}}_{i + 1}^{k + 1} } \\ {\omega_{i + 1}^{k + 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\varvec{X}}_{i + 1}^{k} } \\ {\omega_{i + 1}^{k} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\delta {\varvec{X}}_{i + 1}^{k + 1} } \\ {\omega_{i + 1}^{k + 1} } \\ \end{array} } \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} \ldots . \hfill \\ \end{gathered} $$

(A9)

1.4 Stability and bifurcation analysis with Hill’s method

Hill’s method is well-known for determining a solution branch’s stabilities and bifurcation behaviors in the frequency domain. Suppose that the solution ${\varvec{x}}^{*} (t)$ in the time domain is perturbed with a disturbance term $e^{\Lambda t} {\varvec{s}}(t)$, where $e^{\Lambda t}$ is the decay term and ${\varvec{s}}(t)$ the periodic term:

$$ {\varvec{x}}(t) = {\varvec{x}}^{*} (t) + e^{\Lambda t} {\varvec{s}}(t) $$

(A10)

By substituting Eq. (A10) into Eq. (15) and applying the Galerkin procedure, the following quadratic eigenvalue problem is obtained:

$$ (\Delta_{2} \Lambda^{2} + \Delta_{2} \Lambda + {\varvec{R}}_{{\varvec{X}}} )e^{\Lambda t} {\varvec{S}} = {\mathbf{0}} $$

(A11)

where ${\varvec{S}}$ are the complex eigenvectors and

$$ \begin{gathered} \Delta_{1} = 2\omega \nabla \otimes {\varvec{M}} + {\varvec{I}}_{2H + 1} \otimes {\varvec{C}} \hfill \\ \Delta_{2} = {\varvec{I}}_{2H + 1} \otimes {\varvec{M}} \hfill \\ \end{gathered} $$

(A12)

Then, the Hill’s eigenvalues can be obtained from

$$ ({\varvec{H}} - \Lambda {\varvec{I}}_{2L} ){\varvec{Q}} = {\mathbf{0}} $$

(A13)

where ${\varvec{H}}$ is consistent with the Hill matrix in the state space, which can be expressed as

$$ {\varvec{H}} = \left[ {\begin{array}{*{20}c} 0 & {{\varvec{I}}_{L} } \\ { - \Delta_{2}^{ - 1} {\varvec{R}}_{{\varvec{X}}} } & { - \Delta_{2}^{ - 1} \Delta_{1} } \\ \end{array} } \right] $$

(A14)

Note that $2L = 2n \times (2H + 1)$ eigenvalues can be obtained from Eq. (41), but only $2n$ of them have the physical meaning and correspond to the Floquet exponents, denoted by $\lambda_{i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2, \ldots ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2n$ in the following. Selecting the $2n$ eigenvalues with the smallest imaginary part in the modulus is widely used to approximate Floquet exponents [43]. Once the approximated Floquet exponents are filtered, the stability and bifurcation behaviors of a periodic solution can thus be analyzed by observing their evolvement.