Abstract
In this study, a method for entangling two spatially separated output laser fields from an optomechanical cavity is proposed. In the existing standard methods, entanglement is created by driving the two-mode squeezing part of the linearized optomechanical interaction;, however our method generates entanglement using the quantum back-action nullifying meter technique. As a result, entanglement can be generated outside the blue sideband frequency in both resolved and unresolved sideband regimes. We further show that the system is stable in the entire region where the Duan criterion for inseparability is fulfilled. The effect of thermal noise on the generated entanglement is examined. Finally, we compare this technique with standard methods for entanglement generation using optomechanics.
Similar content being viewed by others
1 Introduction
One of the most exciting features of quantum mechanics is entanglement [1, 2] which is a prerequisite for most quantum technologies, such as quantum key distribution [3], quantum metrology [4–6], quantum information [7, 8], and quantum teleportation [9, 10]. Entanglement has been observed in several microscopic systems such as atoms [11, 12], ions [13, 14], and mechanical mirrors [15–17]. Entanglement can be created in localized objects or propagating (also known as flying) modes. Entanglement in flying modes [18] is more suitable for quantum communication [19, 20] applications, while the entanglement between localized objects is applicable for quantum storage [21, 22]. The rate [18, 23] of discrete entangled pair production is another critical parameter for quantum technologies. Instead of producing discrete entangled pairs, entanglement can also be created with continuous variables. In this study, optomechanics is used to generate continuous variable entanglement between two propagating laser fields.
An optomechanical cavity (OMC) couples [24–27] the optical degrees of freedom with the mechanical degrees of freedom through an oscillating optomechanical mirror [28–31]. The radiation pressure force inside the OMC displaces the optomechanical mirror, changing the cavity length and the properties of the output field from the OMC. The quantum nature of the radiation pressure force can induce quantum mechanical perturbation on the OMM and vice-versa. In particular, OMC has been used to create entanglement between cavity fields [32–36], between cavity field and mechanical oscillator [37–42], and between two mechanical oscillators [15–17, 43–48]. In optomechanics [32, 49–51], entanglement is generated by reducing the interaction Hamiltonian into a beam splitter Hamiltonian and a two-mode squeezing Hamiltonian. The beam splitter interaction transfers the two-mode squeezing interaction with a third mode to create entanglement between two optical modes. In this study, the quantum back-action nullifying meter technique is used to generate continuous variable entanglement between two propagating laser fields. This technique can create entanglement in both resolved and unresolved sideband regimes without driving the blue sideband. For experimentally feasible parameters [52], the entanglement generated between the optical modes using this technique can survive up to room temperature. Although there are several mathematical conditions [53–59] for evaluating entanglement, we specifically use Duan criterion [55] because it is a sufficient condition to establish entanglement.
2 System
An optical cavity with a mirror in the middle (MIM) as shown in Fig. 1 is considered. The partially transparent mirrors \(m_{1}\) and \(m_{2}\) are rigidly fixed, while the perfectly reflective MIM oscillates simple harmonically with an instantaneous position ẑ. The MIM divides the total cavity into subcavity 1 (SC1) and subcavity 2 (SC2) and each has an average length l and an eigenfrequency \(\omega _{e}\). The annihilation operators for the optical field in SC1 and SC2 are represented by â and ĉ, respectively. No tunneling of â into ĉ and vice-versa occurs since, the MIM is perfectly reflective. SC1 and SC2 are driven by input laser fields with annihilation operators \(\hat{a}_{in}\) and \(\hat{c}_{in}\), respectively. The output fields from SC1 and SC2 are represented by the annihilation operators \(\hat{a}_{out}\) and \(\hat{c}_{out}\), respectively. The Hamiltonian Ĥ of the optomechanical cavity is given [60] as follows:
where p̂, \(\omega _{m}\) and m are the momentum, eigenfrequency, and effective mass of the mechanical oscillator, respectively. \(\hat{x}_{o} = \hat{o}^{\dagger}+\hat{o}\) and \(\hat{y}_{o}=i(\hat{o}^{\dagger}-\hat{o})\), where \(o = a, c\), are the dimensionless amplitude and phase quadratures, respectively. \(\hat{H}_{r}\) is the Hamiltonian for the environment and its coupling with OMC and \(g = \omega _{e}/l\) [61–63] is the optomechanical coupling constant. The detuning \(\Delta =\omega _{e}-\omega _{l}\) with \(\omega _{l}\) as the frequency of the driving fields.
Optomechanical cavity with perfectly reflective mechanical mirror in the middle. The mirrors \(m_{1}\) and \(m_{2}\) are rigidly fixed, while the center optomechanical mirror can oscillate. The instantaneous position of the optomechanical mirror is given by ẑ. Entanglement in the output fields is confirmed using the Duan criterion, which is a sufficient condition to establish entanglement
The dynamics of the optomechanical interaction are given as follows:
where ζ is the cavity field decay rate, γ is the decay rate of the MIM and ϖ̂ is the thermal noise operator whose correlation is given [64] as \(\langle \hat{\varpi}(\omega )\hat{\varpi}(\omega ')\rangle =\hbar m \omega \gamma [1+\coth (\hbar \omega /2k_{B}T)]\delta (\omega + \omega ')\) with \(k_{B}\) the Boltzmann constant, T the temperature. \(\hat{x}_{o}^{in} = \hat{o}_{in}^{\dagger}+\hat{o}_{in}\), and \(\hat{y}_{o}^{in}=i(\hat{o}_{in}^{\dagger}-\hat{o}_{in})\) with \(o=a,c\). The operators \(\hat{a}_{in}\) and \(\hat{c}_{in}\) are the annihilation operators for the input fields to SC1 and SC2, respectively. \(\hat{a}_{in}\) and \(\hat{c}_{in}\) are normalized such that their optical powers are given as \(\hbar \omega _{l} \langle \hat{a}_{in}^{\dagger }\hat{a}_{in} \rangle \) and \(\hbar \omega _{l} \langle \hat{c}_{in}^{\dagger }\hat{c}_{in} \rangle \), respectively. We linearize Eqs. (2)-(4) by writing \(\hat{O}=\bar{O}+\hat{\delta}_{O}\), for \(O = a,c,a_{in},c_{in}\), with Ō as the mean value and \(\hat{\delta}_{O}\) as the quantum fluctuation. By adjusting the optical fields in SC1 and SC2 such that \(\bar{x}_{a} = \bar{x}_{c}\) and \(\bar{y}_{a}=\bar{y}_{c}\), the classical radiation pressure forces on the MIM from SC1 and SC2 are equal and opposite in direction. Then, the mean equilibrium position of the MIM is \(\bar{z}=0\). We further set the optical fields in SC1 and SC2 to be real values by adjusting the phase of the input fields as \(\bar{a}_{in}=\bar{c}_{in} = Ee^{-i\phi}\), where \(\phi =\tan ^{-1}(-2\Delta /\zeta )\), with Ē being a real quantity(see the Appendix). Now, the equations of motion for the linearized quantum fluctuations can be written as follows:
where \(\hat{X}_{O} = \hat{\delta}_{O}^{\dagger}+\hat{\delta}_{O}\), \(\bar{x}_{O}=\bar{O}^{*}+\bar{O}\), \(\bar{y}_{O}=i( \bar{O}^{*}-\bar{O})\) and \(\hat{Y}_{O}=i(\hat{\delta}_{O}^{\dagger}-\hat{\delta}_{O})\) with \(O = a,c\). Similarly \(\hat{X}_{O}^{in} = \hat{\delta}_{O_{in}}^{\dagger}+\hat{\delta}_{O_{in}}\), \(\hat{X}_{O}^{out} = \hat{\delta}_{O_{out}}^{\dagger}+\hat{\delta}_{O_{out}}\), \(\hat{Y}_{O}^{in}=i(\hat{\delta}_{O_{in}}^{\dagger}-\hat{\delta}_{O_{in}})\) and \(\hat{Y}_{O}^{out}=i(\hat{\delta}_{O_{out}}^{\dagger}-\hat{\delta}_{O_{out}})\). We have used the relationships \(\bar{y}_{a}=\bar{y}_{c}=0\), \(\bar{x}_{a}=\bar{x}_{c}=2\bar{a}:=\bar{x}\) and \(\bar{z} = 0\) in Eqs. (5)-(7) since, we assumed that \(\bar{a}=\bar{c}\) and \(\bar{a}=\sqrt{\zeta |\bar{E}|^{2}/(\Delta ^{2}+\zeta ^{2}/4)}\) are real. By using the Fourier transform function \(\mathfrak{F}(\hat{O}) = \int _{-\infty}^{\infty} \hat{O}e^{i\omega t}\,dt/ \sqrt{2\pi}\), and Eq. (5)-Eq. (7), the quadratures of the output field can be written in terms of the input field quadratures using the input-output relations [65] as follows:
where the following applies:
with \(\alpha (\omega )=\hbar g^{2}\bar{x}^{2}/[m(\omega _{m}^{2}-\omega ^{2}-i \gamma \omega )]\). The Duan criterion, is a sufficient condition [55] to establish entanglement, and its verification is sufficient to confirm the entanglement between \(\hat{a}_{out}\) and \(\hat{c}_{out}\). Equations (9) and (8) are conducive to evaluating the Duan criterion for verifying the entanglement between \(\hat{a}_{out}\) and \(\hat{c}_{out}\). However, the commutation relationships for these propagating fields [66, 67] are proportional to the Dirac delta distribution. For example, in the case of input fields, \([\hat{x}_{a}^{in}(t),\hat{y}_{a}^{in}(t_{1})]=2i \delta (t-t_{1})\). The divergence arising from the Dirac delta can be approached by considering the finite time τ of the measurement. This finite measurement time leads to a finite bandwidth of \(1/2\tau \) around the frequency \(\omega _{f}\) at which the data are collected. The effect of the finite time of measurement τ can be modeled by using the filter function \(\phi _{\tau}\) as described in Ref. [68]. An important property of \(\phi _{\tau}\) is, that for a generic function \(f(\omega )\), we can write the following:
where \(\delta _{\omega _{f}\omega '_{f}}\) is the Kronecker delta. \(\omega _{f}\) in Eq. (10) is constant, and its value is chosen according to our needs. We choose \(\omega _{f} = 0\) because it corresponds to the output field frequency. The relationship between the frequency filtered quadratures \(\hat{X}_{a_{f}}^{out}\) and \(\hat {X}_{a}^{out}\) can be written as \(\hat{X}_{a_{f}}^{out}=\int _{-\infty}^{\infty}\,d\omega e^{-i\omega t} \phi _{\tau}(\omega )\hat{X}_{a}^{out}(\omega )\). Similarly \(\hat{Y}_{a_{f}}^{out}=\int _{-\infty}^{\infty}\,d\omega e^{-i\omega t} \phi _{\tau}(\omega )\hat{Y}_{a}^{out}(\omega )\). We can write similar relationships for the quadratures of \(\hat{c}_{out}\). Then, we can write the following:
By assuming that τ is much larger than any other characteristic time of the system, and by substituting Eq. (8) and Eq. (9) in Eq. (11) and Eq. (12), the Duan criterion can be expressed as follows:
By using the stationary property of the input fields and Eq. (1), we can also verify that \([\hat{X}_{a_{f}}^{out},\hat{Y}_{a_{f}}^{out}]=[\hat{X}_{c_{f}}^{out}, \hat{Y}_{c_{f}}^{out}]=2i\).
3 Results
Eq. (9) is independent of the optomechanical coupling constant g and cannot be influenced by the radiation pressure coupling. A straightforward calculation shows that \(|e_{4}-ie_{5}|^{2} = 1\) and \(\langle (\hat{X}_{a_{f}}^{out}+\hat{X}_{c_{f}}^{out})^{2}\rangle =2\). On the other hand, g enters into Eq. (8) through \(\alpha (\omega )\). Hence, tweaking the radiation pressure force can modify the \(\langle (\hat{Y}_{a_{f}}^{out}-\hat{Y}_{c_{f}}^{out})^{2}\rangle \) term. The presence of g in the \(e_{2}\) term of Eq. (8) leads to radiation pressure noise (RPN). Here, we can use RPN suppression techniques to suppress the X̂ quadrature strength in Eq. (9). While several techniques [69–73] for suppressing the RPN are available, we implement the quantum back-action nullifying meter (QBNM) technique [74] since, it allows the suppression of quantum back-action when \(\omega \to 0\). Without going into the details [75] of the RPN suppression, it is simpler to prove entanglement by minimizing \(e_{1}\) and \(e_{2}\). To achieve this, we redefine \(\alpha (0)-\Delta =u\Delta \) and \(\Delta =v\zeta /2\) where u and v are arbitrary real numbers. Then, we can write the following:
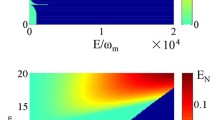
Note that we disregard the thermal noise term in Eq. (14). Since we already estimated that \(\langle (\hat{X}_{a_{f}}^{out}+\hat{X}_{c_{f}}^{out})^{2}\rangle = 2\), according to the Duan criterion, the sufficient condition for \(\hat{a}_{out}\) and \(\hat{c}_{out}\) to be entangled is \(\langle (\hat{Y}_{a_{f}}^{out}-\hat{Y}_{c_{f}}^{out})^{2}\rangle <2\). From Eq. (14), this condition can be satisfied only if \(v^{2}u(1+u)<0\). For \(u\neq0\) and \(v\neq0\), Duan’s criterion for entanglement is satisfied when \(-1< u<0\). The stability of the system is examined using Eq. (2) to Eq. (4) for generic OM parameters. After rewriting ẑ and p̂ in terms of the dimensionless position and momentum operators, the number of eigenvalues with positive real values for the drift matrix is shown in Fig. 2. Since no eigenvalues exists with a positive real part in the region \(-1< u<0\), the stability of the system is ensured in the region where the Duan criterion for inseparability is satisfied. Minimizing the RHS of Eq. (14) further reveals that the smallest possible value for Eq. (14) is \(2/[1+(2\Delta /\zeta )^{2}]\) at \(\alpha (0)=\Delta [1+(2\Delta /\zeta )^{2}]/[2+(2\Delta /\zeta )^{2}]\). Since \(\alpha (0)\) stems from the radiation pressure force, the input laser power P corresponding to the lowest value of Eq. (14) is as follows:
We reevaluate Eq. (13) by substituting Eq. (15) and rewrite it as follows:
where the LHS of Eq. (16) is the Duan criterion when the input laser power determined using Eq. (15).
Number of eigenvalues with positive real values as functions of u, v and Q where \(Q=\omega _{m}/\gamma \). The simulation parameters are as follows: \(\zeta /2\pi = 15.9\times 10^{6}\) Hz, \(\gamma /2\pi =1.09\times 10^{-3}\) Hz, and \(\alpha (0)=(u+1)v\zeta /2\). The blue (black) legend represents the area with two (one) eigenvalues with positive real parts. The colorless area represents no (or zero) eigenvalues with a positive real part
As \(2\Delta /\zeta \to \infty \), the RHS of Eq. (16) approaches 2 when the thermal noise is disregarded. Hence, practically, the Duan criterion can never be less than or equal to 2 for the technique described in this study. For \(2\Delta /\zeta \gg 1\), \(\alpha (0)\) will be approximately equal to Δ; this is the same condition required for QBNM [74]. The \(e_{2}\) term disappears from Eq. (8) for \(\alpha (0) = \Delta \), and this leads to the suppression of radiation pressure noise. The entanglement condition \(\alpha (0)=\Delta [1+(2\Delta /\zeta )^{2}]/[2+(2\Delta /\zeta )^{2}]\), leads to quantum cross-correlations between \(\hat{Y}_{a}^{out}\) and \(\hat{Y}_{c}^{out}\) such that the output fields from SC1 and SC2 are entangled. By using Eq. (13), Fig. 3 is plotted with the Duan criterion on the vertical axis and input laser power on the horizontal axis for \(2\Delta /\zeta = 5\). The Duan criterion has an exact minimum value when the input laser power is determined using Eq. (15). Similarly, the lowest value of the Duan criterion for the curve is determined using Eq. (16). The thick green curve in Fig. 4 shows the plot of Eq. (16) as a function of \(2\Delta /\zeta \) with thermal noise at \(T=300\) K. The input laser power in Fig. 4 is determined using Eq. (15) for each point of \(2\Delta /\zeta \). According to the red dotted curve, the value of Eq. (16) gradually decreases to 2 with increasing \(2\Delta /\zeta \) when thermal noise is not considered. However, increasing the \(2\Delta /\zeta \) value also increases the thermal noise, and eventually the Duan criterion value is increased to a value greater than four, as shown by the green curve. The effect of thermal noise on entanglement is examined in the next section.
Duan criterion as a function of input laser power for \(2\Delta /\zeta =5\). Entanglement is created when the Duan criterion is less than 4. The inset figure shows a magnified plot of the marked area. The simulation parameters are as follows [52]: \(m=2.3\times 10^{-12}\) kg, \(\zeta /2\pi = 15.9\times 10^{6}\) Hz, \(\omega _{m}/2\pi =1.14\times 10^{6}\) Hz, \(g=4.45\times 10^{17}\) Hz/m, \(\omega _{l}/2\pi =3.77\times 10^{14}\) Hz, \(\gamma /2\pi =1.09\times 10^{-3}\) Hz, and \(T = 300\) K
3.1 Comparison with existing methods
To show the novelty of the technique described in this article, we compare it with the existing methods [16, 32, 35, 37, 45, 51, 76–80] for entanglement generation using optomechanics. In this paragraph, we describe how the existing method can generate entanglement for OMC, as shown in Fig. 1. In the next paragraph we compare and contrast the method described in this study with the existing method. The existing method theorizes entanglement by linearizing the optomechanical interaction Hamiltonian into a beam splitter and two-mode squeezing Hamiltonians. As shown in Fig. 5, driving the OMC on the blue (\(\omega _{e}+\omega _{m}\)) or red (\(\omega _{e}- \omega _{m}\)) sidebands enhances, the two-mode squeezing \(\hat{a}^{\dagger}\hat{b}^{\dagger}+\hat{a}\hat{b}\) or beam splitter \(\hat{a}^{\dagger}\hat{b}+\hat{b}^{\dagger}\hat{a}\) interaction, respectively, where b̂ is the annihilation operator for the mechanical oscillator. Thus, driving SC1 (see Fig. 1) at the \(\omega _{e}+\omega _{m}\) frequency enhances the two-mode squeezing interaction between the mechanical mode b̂ and the optical mode â. This leads to entanglement between â and b̂. Driving SC2 at its red sideband enhances the beam-splitter interaction between b̂ and ĉ. This leads to the transfer of entangled state from b̂ to ĉ, thus creating entanglement between the optical fields â and ĉ. The same technique has also been used for other bosonic systems [81, 82]. Propagating fields are entangled using the same physics in the unresolved regime \((\omega _{m}\ll \zeta )\), as shown in Ref. [76]. Ref. [76] used two driving fields to create four sidebands leading to quadripartite interactions in the unresolved regime. Since the sidebands are not resolved, resonantly driving the OMC entangles the output fields.
\(\hat{a}~(\hat{b})\) is the annihilation operator for the cavity (mechanical) mode. The center peak is the cavity mode with linewidth ζ. The blue and red arrows are the sidebands at frequencies \(\omega _{e}+\omega _{m}\) and \(\omega _{e}-\omega _{m}\), respectively. As shown in the blue sideband, driving the OMC at the \(\omega _{e}+\omega _{m}\) frequency enhances the two-mode squeezing (entangling) interaction. Similarly, as shown in the red sideband, driving the OMC at the \(\omega _{e}-\omega _{m}\) frequency enhances the quantum state transfer (beam splitter) interaction. The sidebands are resolved when \(\omega _{m}\gg \zeta \)
Overall, driving the blue sideband is an essential requirement for entanglement in the existing methods. No such requirement exists for the technique described in this study since, the optomechanical interaction Hamiltonian does not need to be reduced to a two-mode squeezing Hamiltonian. In our method, under appropriate detuning, the optical restoring force will counteract the linearized quantum radiation pressure force. This modifies the radiation pressure force contribution in the output field quadratures leading to entanglement. The maximum violation of the Duan criterion for separability is observed in our method when the input power is calculated using Eq. (15), which is close to the QBNM condition. Both the sideband driving, and the resolved and unresolved regimes (or \(\omega _{m}/\zeta \) values) are also unimportant in our method. In our scheme, two tone driving is not required because both optical modes can be equally detuned from the cavity resonance.
3.2 Temperature dependence
The thermal robustness of the entanglement is shown in Fig. 6 for different \(2\Delta /\zeta \) values. The vertical and horizontal axes in Fig. 6 correlate to Eq. (16) and the temperature, respectively. The input laser power is calculate using Eq. (15) for each \(2\Delta /\zeta \) curve in Fig. 6. The generated entanglement survives up to room temperature. The thermal robustness of entanglement can be understood by rewriting the thermal noise term in Eq. (13) follows: as
where \(Q=\omega _{m}/\gamma \), and we use Eq. (15) to evaluate Eq. (17). The MIM can be decoupled from the thermal environment when the ratio [25, 83] \(2\pi k_{B}T/(\hbar Q\omega _{m})\) is far greater than one. Hence, the high quality factor of the MIM used in Ref. [52] causes the entanglement to be immune to the thermal noise at room temperature. Eq. (16) confirms that a large \(2\Delta /\zeta \) value minimizes the Duan criterion in the absence of thermal noise. On the other hand, a large \(2\Delta /\zeta \) increases the thermal noise, as shown in Eq. (17). Hence the ideal scenario is \(2\pi k_{B}T/(\hbar Q \omega _{m})\ll 1\ll 2\Delta /\zeta \), and is achievable for a wide range of \(2\Delta /\zeta \) ratios as shown by the green curve in Fig. 4. This condition indicates that the MIM does not need to be in the ground state to entangle the output fields.
The technique described in this work can be experimentally achieved in OMC with MIM [28]. This configuration can also be attained by using photonic bandgap structures [61, 84, 85] or microtoroidal structures [62] as described in Refs. [61, 63]. To improve the thermal robustness of the entanglement, MIMs with high quality factors such as those in Refs. [52, 76] can be used. In the conventional method, entanglement is created between the MIM and the optical mode through two-mode squeezing interactions. Thus, the entanglement cannot survive once the thermal noise from the MIM destroys the two-mode squeezed state. According to the method described in this study, the MIM acts as a mediator to transfer the correlations between the optical fields. As the optical field and MIM do not need to be in a two-mode squeezed state, the optical fields can be entangled even at room temperature by using high quality MIM.
4 Conclusion
A new method for generating entanglement between two spatially separated propagating laser fields is presented. By using an optical cavity with an MIM, the quantum properties of the optical field from one subcavity are written onto the optical field in the other. This leads to quantum correlations between the two laser fields exiting the optical cavity. We derived the conditions under which these correlations can lead to entanglement between the two output fields. The underlying physics for the entanglement generation can be attributed to the QBNM technique. The robustness of the generated entanglement against the temperature is studied. Entanglement can be generated even at room temperature for experimentally feasible parameters in both resolved and unresolved sideband regimes.
Availability of data and materials
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Code availability
The code used for simulating the plots is available from the corresponding author on reasonable request.
Abbreviations
- OMC:
-
optomechanical cavity
- MIM:
-
mirror in middle
- SC1:
-
subcavity 1
- SC2:
-
subcavity 2
- RPN:
-
radiation pressure noise
- QBNM:
-
quantum back-action nullifying meter
References
Hensen B, Bernien H, Dréau AE, Reiserer A, Kalb N, Blok MS, Ruitenberg J, Vermeulen RFL, Schouten RN, Abellán C, Amaya W, Pruneri V, Mitchell MW, Markham M, Twitchen DJ, Elkouss D, Wehner S, Taminiau TH, Hanson R. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature. 2015;526(7575):682–6. https://doi.org/10.1038/nature15759.
Friis N, Marty O, Maier C, Hempel C, Holzäpfel M, Jurcevic P, Plenio MB, Huber M, Roos C, Blatt R, Lanyon B. Observation of entangled states of a fully controlled 20-qubit system. Phys Rev X. 2018;8:021012. https://doi.org/10.1103/PhysRevX.8.021012.
Madsen LS, Usenko VC, Lassen M, Filip R, Andersen UL. Continuous variable quantum key distribution with modulated entangled states. Nat Commun. 2012;3(1):1083. https://doi.org/10.1038/ncomms2097.
Yan ZF, He B, Lin Q. Optomechanical force sensor operating over wide detection range. Opt Express. 2023;31(10):16535–48. https://doi.org/10.1364/OE.486667.
Yan ZF, He B, Lin Q. Force sensing with an optomechanical system at room temperature. Phys Rev A. 2023;107(1):013529.
Lee C-W, Lee JH, Seok H. Squeezed-light-driven force detection with an optomechanical cavity in a Mach–Zehnder interferometer. Sci Rep. 2020;10(1):17496. https://doi.org/10.1038/s41598-020-74629-1.
Braunstein SL, Loock P. Quantum information with continuous variables. Rev Mod Phys. 2005;77:513–77. https://doi.org/10.1103/RevModPhys.77.513.
Kimble HJ. The quantum Internet. Nature. 2008;453(7198):1023–30. https://doi.org/10.1038/nature07127.
Furusawa A, Sørensen JL, Braunstein SL, Fuchs CA, Kimble HJ, Polzik ES. Unconditional quantum teleportation. Science. 1998;282(5389):706–9. https://www.science.org/doi/pdf/10.1126/science.282.5389.706. https://doi.org/10.1126/science.282.5389.706.
Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett. 1993;70:1895–9. https://doi.org/10.1103/PhysRevLett.70.1895.
Ritter S, Nölleke C, Hahn C, Reiserer A, Neuzner A, Uphoff M, Mücke M, Figueroa E, Bochmann J, Rempe G. An elementary quantum network of single atoms in optical cavities. Nature. 2012;484(7393):195–200. https://doi.org/10.1038/nature11023.
Hofmann J, Krug M, Ortegel N, Gérard L, Weber M, Rosenfeld W, Weinfurter H. Heralded entanglement between widely separated atoms. Science. 2012;337(6090):72–5. https://www.science.org/doi/pdf/10.1126/science.1221856. https://doi.org/10.1126/science.1221856.
Rowe MA, Kielpinski D, Meyer V, Sackett CA, Itano WM, Monroe C, Wineland DJ. Experimental violation of a bell’s inequality with efficient detection. Nature. 2001;409(6822):791–4. https://doi.org/10.1038/35057215.
Blatt R, Wineland D. Entangled states of trapped atomic ions. Nature. 2008;453(7198):1008–15. https://doi.org/10.1038/nature07125.
Xiong B, Li X, Chao S-L, Yang Z, Zhang W-Z, Zhou L. Generation of entangled Schrödinger cat state of two macroscopic mirrors. Opt Express. 2019;27(9):13547–58. https://doi.org/10.1364/OE.27.013547.
Huang S, Agarwal GS. Entangling nanomechanical oscillators in a ring cavity by feeding squeezed light. New J Phys. 2009;11(10):103044. https://doi.org/10.1088/1367-2630/11/10/103044.
Vitali D, Mancini S, Tombesi P. Stationary entanglement between two movable mirrors in a classically driven fabry–perot cavity. J Phys A, Math Theor. 2007;40(28):8055. https://doi.org/10.1088/1751-8113/40/28/S14.
Deng ZJ, Yan X-B, Wang Y-D, Wu C-W. Optimizing the output-photon entanglement in multimode optomechanical systems. Phys Rev A. 2016;93:033842. https://doi.org/10.1103/PhysRevA.93.033842.
Bennett CH, Wiesner SJ. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys Rev Lett. 1992;69:2881–4. https://doi.org/10.1103/PhysRevLett.69.2881.
Gisin N, Thew R. Quantum communication. Nat Photonics. 2007;1(3):165–71. https://doi.org/10.1038/nphoton.2007.22.
Sete EA, Eleuch H. High-efficiency quantum state transfer and quantum memory using a mechanical oscillator. Phys Rev A. 2015;91:032309. https://doi.org/10.1103/PhysRevA.91.032309.
Lvovsky AI, Sanders BC, Tittel W. Optical quantum memory. Nat Photonics. 2009;3(12):706–14. https://doi.org/10.1038/nphoton.2009.231.
Deng ZJ, Habraken SJM, Marquardt F. Entanglement rate for Gaussian continuous variable beams. New J Phys. 2016;18(6):063022. https://doi.org/10.1088/1367-2630/18/6/063022.
Kippenberg TJ, Vahala KJ. Cavity opto-mechanics. Opt Express. 2007;15(25):17172–205. https://doi.org/10.1364/OE.15.017172.
Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity optomechanics. Rev Mod Phys. 2014;86:1391–452. https://doi.org/10.1103/RevModPhys.86.1391.
Meystre P. A short walk through quantum optomechanics. Ann Phys. 2013;525(3):215–33.
Kippenberg TJ, Vahala KJ. Cavity optomechanics: back-action at the mesoscale. Science. 2008;321(5893):1172–6. https://www.science.org/doi/pdf/10.1126/science.1156032. https://doi.org/10.1126/science.1156032.
Bhattacharya M, Uys H, Meystre P. Optomechanical trapping and cooling of partially reflective mirrors. Phys Rev A. 2008;77:033819. https://doi.org/10.1103/PhysRevA.77.033819.
Jayich AM, Sankey JC, Zwickl BM, Yang C, Thompson JD, Girvin SM, Clerk AA, Marquardt F, Harris JGE. Dispersive optomechanics: a membrane inside a cavity. New J Phys. 2008;10(9):095008. https://doi.org/10.1088/1367-2630/10/9/095008.
Thompson JD, Zwickl BM, Jayich AM, Marquardt F, Girvin SM, Harris JGE. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature. 2008;452(7183):72–5. https://doi.org/10.1038/nature06715.
Saarinen SA, Kralj N, Langman EC, Tsaturyan Y, Schliesser A. Laser cooling a membrane-in-the-middle system close to the quantum ground state from room temperature. Optica. 2023;10(3):364–72. https://doi.org/10.1364/OPTICA.468590.
Wang Y-D, Clerk AA. Reservoir-engineered entanglement in optomechanical systems. Phys Rev Lett. 2013;110:253601. https://doi.org/10.1103/PhysRevLett.110.253601.
Pirandola S, Mancini S, Vitali D, Tombesi P. Continuous variable entanglement by radiation pressure. J Opt B, Quantum Semiclass Opt. 2003;5(4):523. https://doi.org/10.1088/1464-4266/5/4/359.
Giovannetti V, Mancini S, Tombesi P. Radiation pressure induced Einstein-Podolsky-Rosen paradox. Europhys Lett. 2001;54(5):559. https://doi.org/10.1209/epl/i2001-00284-x.
Kuzyk MC, Enk SJ, Wang H. Generating robust optical entanglement in weak-coupling optomechanical systems. Phys Rev A. 2013;88:062341. https://doi.org/10.1103/PhysRevA.88.062341.
Paternostro M, Vitali D, Gigan S, Kim MS, Brukner C, Eisert J, Aspelmeyer M. Creating and probing multipartite macroscopic entanglement with light. Phys Rev Lett. 2007;99:250401. https://doi.org/10.1103/PhysRevLett.99.250401.
Chen ZX, Lin Q, He B, Lin ZY. Entanglement dynamics in double-cavity optomechanical systems. Opt Express. 2017;25(15):17237–48. https://doi.org/10.1364/OE.25.017237.
Liu J-H, Zhang Y-B, Yu Y-F, Zhang Z-M. Entangling cavity optomechanical systems via a flying atom. Opt Express. 2017;25(7):7592–603. https://doi.org/10.1364/OE.25.007592.
Vitali D, Gigan S, Ferreira A, Böhm HR, Tombesi P, Guerreiro A, Vedral V, Zeilinger A, Aspelmeyer M. Optomechanical entanglement between a movable mirror and a cavity field. Phys Rev Lett. 2007;98:030405. https://doi.org/10.1103/PhysRevLett.98.030405.
Liu Z-Q, Hu C-S, Jiang Y-K, Su W-J, Wu H, Li Y, Zheng S-B. Engineering optomechanical entanglement via dual-mode cooling with a single reservoir. Phys Rev A. 2021;103:023525. https://doi.org/10.1103/PhysRevA.103.023525.
Li G, Nie W, Li X, Chen A. Dynamics of ground-state cooling and quantum entanglement in a modulated optomechanical system. Phys Rev A. 2019;100:063805. https://doi.org/10.1103/PhysRevA.100.063805.
Aoune D, Habiballah N. Quantifying of quantum correlations in an optomechanical system with cross-Kerr interaction. J Russ Laser Res. 2022;43(4):406–15. https://doi.org/10.1007/s10946-022-10065-y.
Chakraborty S, Sarma AK. Entanglement dynamics of two coupled mechanical oscillators in modulated optomechanics. Phys Rev A. 2018;97:022336. https://doi.org/10.1103/PhysRevA.97.022336.
Amazioug M, Maroufi B, Daoud M. Creating mirror–mirror quantum correlations in optomechanics. Eur Phys J D. 2020;74(3):54. https://doi.org/10.1140/epjd/e2020-100518-7.
Liao J-Q, Wu Q-Q, Nori F. Entangling two macroscopic mechanical mirrors in a two-cavity optomechanical system. Phys Rev A. 2014;89:014302. https://doi.org/10.1103/PhysRevA.89.014302.
Gröblacher S, Hammerer K, Vanner MR, Aspelmeyer M. Observation of strong coupling between a micromechanical resonator and an optical cavity field. Nature. 2009;460(7256):724–7. https://doi.org/10.1038/nature08171.
Pirandola S, Vitali D, Tombesi P, Lloyd S. Macroscopic entanglement by entanglement swapping. Phys Rev Lett. 2006;97:150403. https://doi.org/10.1103/PhysRevLett.97.150403.
Pinard M, Dantan A, Vitali D, Arcizet O, Briant T, Heidmann A. Entangling movable mirrors in a double-cavity system. Europhys Lett. 2005;72(5):747. https://doi.org/10.1209/epl/i2005-10317-6.
Yin Z-Q, Han Y-J. Generating epr beams in a cavity optomechanical system. Phys Rev A. 2009;79:024301. https://doi.org/10.1103/PhysRevA.79.024301.
Yan X-B. Enhanced output entanglement with reservoir engineering. Phys Rev A. 2017;96:053831. https://doi.org/10.1103/PhysRevA.96.053831.
Hofer SG, Wieczorek W, Aspelmeyer M, Hammerer K. Quantum entanglement and teleportation in pulsed cavity optomechanics. Phys Rev A. 2011;84:052327. https://doi.org/10.1103/PhysRevA.84.052327.
Rossi M, Mason D, Chen J, Tsaturyan Y, Schliesser A. Measurement-based quantum control of mechanical motion. Nature. 2018;563(7729):53–8. https://doi.org/10.1038/s41586-018-0643-8.
Bell JS. On the Einstein Podolsky Rosen paradox. Physics. 1964;1:195–200. https://doi.org/10.1103/PhysicsPhysiqueFizika.1.195.
Peres A. Separability criterion for density matrices. Phys Rev Lett. 1996;77:1413–5. https://doi.org/10.1103/PhysRevLett.77.1413.
Duan L-M, Giedke G, Cirac JI, Zoller P. Inseparability criterion for continuous variable systems. Phys Rev Lett. 2000;84:2722–5. https://doi.org/10.1103/PhysRevLett.84.2722.
Hillery M, Zubairy MS. Entanglement conditions for two-mode states. Phys Rev Lett. 2006;96:050503. https://doi.org/10.1103/PhysRevLett.96.050503.
Doherty AC, Parrilo PA, Spedalieri FM. Complete family of separability criteria. Phys Rev A. 2004;69:022308. https://doi.org/10.1103/PhysRevA.69.022308.
Simon R. Peres-horodecki separability criterion for continuous variable systems. Phys Rev Lett. 2000;84:2726–9. https://doi.org/10.1103/PhysRevLett.84.2726.
Werner RF, Wolf MM. Bound entangled Gaussian states. Phys Rev Lett. 2001;86:3658–61. https://doi.org/10.1103/PhysRevLett.86.3658.
Law CK. Interaction between a moving mirror and radiation pressure: a Hamiltonian formulation. Phys Rev A. 1995;51:2537–41. https://doi.org/10.1103/PhysRevA.51.2537.
Ludwig M, Safavi-Naeini AH, Painter O, Marquardt F. Enhanced quantum nonlinearities in a two-mode optomechanical system. Phys Rev Lett. 2012;109:063601. https://doi.org/10.1103/PhysRevLett.109.063601.
Grudinin IS, Lee H, Painter O, Vahala KJ. Phonon laser action in a tunable two-level system. Phys Rev Lett. 2010;104:083901. https://doi.org/10.1103/PhysRevLett.104.083901.
Miao H, Danilishin S, Corbitt T, Chen Y. Standard quantum limit for probing mechanical energy quantization. Phys Rev Lett. 2009;103:100402. https://doi.org/10.1103/PhysRevLett.103.100402.
Giovannetti V, Vitali D. Phase-noise measurement in a cavity with a movable mirror undergoing quantum Brownian motion. Phys Rev A. 2001;63:023812. https://doi.org/10.1103/PhysRevA.63.023812.
Gardiner CW, Collett MJ. Input and output in damped quantum systems: quantum stochastic differential equations and the master equation. Phys Rev A. 1985;31:3761–74. https://doi.org/10.1103/PhysRevA.31.3761.
Abram I. Quantum theory of light propagation: linear medium. Phys Rev A. 1987;35:4661–72. https://doi.org/10.1103/PhysRevA.35.4661.
Blow KJ, Loudon R, Phoenix SJD, Shepherd TJ. Continuum fields in quantum optics. Phys Rev A. 1990;42:4102–14. https://doi.org/10.1103/PhysRevA.42.4102.
Zippilli S, Giuseppe GD, Vitali D. Entanglement and squeezing of continuous-wave stationary light. New J Phys. 2015;17(4):043025. https://doi.org/10.1088/1367-2630/17/4/043025.
Caniard T, Verlot P, Briant T, Cohadon P-F, Heidmann A. Observation of back-action noise cancellation in interferometric and weak force measurements. Phys Rev Lett. 2007;99:110801. https://doi.org/10.1103/PhysRevLett.99.110801.
Tsang M, Caves CM. Evading quantum mechanics: engineering a classical subsystem within a quantum environment. Phys Rev X. 2012;2:031016. https://doi.org/10.1103/PhysRevX.2.031016.
Møller CB, Thomas RA, Vasilakis G, Zeuthen E, Tsaturyan Y, Balabas M, Jensen K, Schliesser A, Hammerer K, Polzik ES. Quantum back-action-evading measurement of motion in a negative mass reference frame. Nature. 2017;547(7662):191–5. https://doi.org/10.1038/nature22980.
Vyatchanin SP, Zubova EA. Quantum variation measurement of a force. Phys Lett A. 1995;201(4):269–74. https://doi.org/10.1016/0375-9601(95)00280-G.
Braginsky VB, Vorontsov YI, Thorne KS. Quantum nondemolition measurements. Science. 1980;209(4456):547–57. https://www.science.org/doi/pdf/10.1126/science.209.4456.547. https://doi.org/10.1126/science.209.4456.547.
Davuluri S, Li Y. Light as a quantum back-action nullifying meter. J Opt Soc Am B. 2022;39(12):3121–7. https://doi.org/10.1364/JOSAB.462699.
Subhash S, Das S, Dey TN, Li Y, Davuluri S. Enhancing the force sensitivity of a squeezed light optomechanical interferometer. Opt Express. 2023;31(1):177–91. https://doi.org/10.1364/OE.476672.
Chen J, Rossi M, Mason D, Schliesser A. Entanglement of propagating optical modes via a mechanical interface. Nat Commun. 2020;11(1):943. https://doi.org/10.1038/s41467-020-14768-1.
Barzanjeh S, Redchenko ES, Peruzzo M, Wulf M, Lewis DP, Arnold G, Fink JM. Stationary entangled radiation from micromechanical motion. Nature. 2019;570(7762):480–3. https://doi.org/10.1038/s41586-019-1320-2.
Genes C, Mari A, Vitali D, Tombesi P. Chapter 2 quantum effects in optomechanical systems. In: Advances in atomic molecular and optical physics. vol. 57. San Diego: Academic Press; 2009. p. 33–86. https://doi.org/10.1016/S1049-250X(09)57002-4. https://www.sciencedirect.com/science/article/pii/S1049250X09570024.
Abdi M, Barzanjeh S, Tombesi P, Vitali D. Effect of phase noise on the generation of stationary entanglement in cavity optomechanics. Phys Rev A. 2011;84:032325. https://doi.org/10.1103/PhysRevA.84.032325.
Gut C, Winkler K, Hoelscher-Obermaier J, Hofer SG, Nia RM, Walk N, Steffens A, Eisert J, Wieczorek W, Slater JA, Aspelmeyer M, Hammerer K. Stationary optomechanical entanglement between a mechanical oscillator and its measurement apparatus. Phys Rev Res. 2020;2:033244. https://doi.org/10.1103/PhysRevResearch.2.033244.
Zheng T-A, Zheng Y, Wang L, Liao C-G. Dissipative generation of significant amount of photon-phonon asymmetric steering in magnomechanical interfaces. EPJ Quantum Technol. 2023;10(1):19. https://doi.org/10.1140/epjqt/s40507-023-00177-y.
Barzanjeh S, Vitali D, Tombesi P, Milburn GJ. Entangling optical and microwave cavity modes by means of a nanomechanical resonator. Phys Rev A. 2011;84:042342. https://doi.org/10.1103/PhysRevA.84.042342.
Davuluri S, Li Y. Absolute rotation detection by Coriolis force measurement using optomechanics. New J Phys. 2016;18(10):103047. https://doi.org/10.1088/1367-2630/18/10/103047.
Paraïso TK, Kalaee M, Zang L, Pfeifer H, Marquardt F, Painter O. Position-squared coupling in a tunable photonic crystal optomechanical cavity. Phys Rev X. 2015;5:041024. https://doi.org/10.1103/PhysRevX.5.041024.
Kalaee M, Paraïso TK, Pfeifer H, Painter O. Design of a quasi-2d photonic crystal optomechanical cavity with tunable, large x2-coupling. Opt Express. 2016;24(19):21308–28. https://doi.org/10.1364/OE.24.021308.
Funding
This work is supported by the National Natural Science Foundation of China (Grants No. 12274107 and No. 12074030).
Author information
Authors and Affiliations
Contributions
Authors’ contributions :GG performed the calculations and simulations, and was involved in every aspect of the work and the manuscript preparation. S D and Y L formulated the concept and supervised the work.
Corresponding authors
Ethics declarations
Ethics approval
Not applicable.
Consent for publication
All authors consent for publication.
Consent to participate
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Derivation of conditions for phase ϕ
Appendix: Derivation of conditions for phase ϕ
When writing Eqs. (2)-(4) we set \(\bar{z}=0\) by adjusting the classical radiation pressure force in SC1 and SC2. Here, we quantitatively show the conditions that lead to \(\bar{z}=0\). By using Eq. (1) the dynamics of the mean variables are given as follows:
From Eq. (18), z̄ is set to zero by imposing the condition \(\bar{x}_{a}-\bar{x}_{c}=\bar{y}_{a}=\bar{y}_{c}=0\). Since the optical fields in SC1 and SC2 are independently driven by two separate laser fields, it is possible to set \(\bar{x}_{a}=\bar{x}_{c}\). We can further set that the mean fields in SC1 and SC2 are real; then \(\bar{y}_{a}=\bar{y}_{c}=0\) and hence Eq. (19) indicates that \(\sqrt{\zeta}\bar{x}_{a}=2\bar{x}_{a}^{in}\), while Eq. (20) indicates that \(\sqrt{\zeta}\bar{y}_{a}^{in}=\Delta \bar{x}_{a}\). Using these relationships, we can finally write \(\zeta \bar{y}_{a}^{in}=2\Delta \bar{x}_{a}^{in}\), which indicates the following:
The same reasoning can also be applied to \(\bar{x}_{c}\) and \(\bar{y}_{c}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gopinath, G., Li, Y. & Davuluri, S. Continuous variable entanglement between propagating optical modes using optomechanics. EPJ Quantum Technol. 11, 41 (2024). https://doi.org/10.1140/epjqt/s40507-024-00252-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjqt/s40507-024-00252-y