1 Introduction

In recent years, a variety of quantum systems including atomic ensembles [1], superconducting qubits [2], trapped ions [3], semiconductor quantum dots [4], and spins in magnetic materials or diamonds [5, 6] have become promising candidates for studying the light-matter interactions, which are significantly applied in quantum information processing and quantum computing. Especially, magnons, quanta of collective spin wave excitation in yttrium iron garnet (YIG) as the representative magnetic material, provide a wide platform to build hybrid quantum networks and realize multi-functional quantum tasks via combining various quantum systems with different advantages. The strong and even super-strong couplings between magnons and microwave cavity photons have been reported due to the high spin density of YIG [7, 8], and magnons can also interact with optical photons, superconducting qubits, and phonons [9, 10]. It is noted that the cavity optomagnomechanical system is proposed by means of the magnetostrictive and radiation-pressure interactions mediated by the mechanical motion [11]. In such a hybrid system, some fascinating quantum phenomena have been demonstrated, such as microwave-optical conversion and entanglement [11, 12], atom-magnon entanglement [13], Fano-type optical response and four-wave mixing process [14], and phonon-magnon-photon entanglement [15].

Entanglement is an essential quantum effect in hybrid quantum systems, particularly the multipartite continuous variable entanglement plays a key role in multi-party quantum communication and network [16, 17]. And the nonlocal correlation of macroscopic objects can be widely used in large-scale fundamental testing of quantum mechanics, quantum to classical transitions, and building more powerful sensing, communication, processing, and storage devices [18–20]. In cavity optomechanics, significant progress has been made in the study of macroscopic entanglement via the optomechanical radiation pressure [21], where the entanglements of two distant macroscopic mechanical resonators and between the massive mechanical oscillator and the electromagnetic field or collective atomic spin oscillator have been reported [22–26]. Apart from the optomechanical system, cavity magnonics has gradually become an advantageous platform for studying macroscopic quantum entanglement [9, 10]. For example, two long-distance ferrimagnetic spheres can be entangled by exploiting the magnetostrictive interaction [27], squeezed-reservoir engineering [28], nonlinear Kerr effect of magnons [29], etc. Tan et al. [30] proposed a scheme to entangle a macroscopic mechanical motion and a YIG sphere mediated by the electromagnetic cavity far beyond the sideband-resolved regime. And Zhong et al. [31] recently presented that the macroscopic tripartite entanglement and steering of three YIG spheres can be achieved by a squeezed reservoir. Moreover, the multipartite quantum correlations among the magnons, photons, phonons, and atoms have been studied [32–37].

Nonreciprocity representing the unidirectional invisibility of light in propagation has been an indispensable tool to construct the optical functional components and complex information processing network [38]. Recently, the Fizeau light-dragging effect induced by spinning the optical resonator leads to a positive or negative frequency shift of optical frequency, which has become an experimentally feasible approach to explore various quantum nonreciprocal phenomena including nonreciprocal photon blockade [39, 40], quantum entanglement and steering [31, 37, 41, 42], phonon laser [43], and sideband responses [44]. Interestingly, Wang et al. [45] theoretically show the nonreciprocal magnon blockade could be generated based on the microwave cavity-mediated qubit-magnon coherent and dissipative couplings at the quantum limit level. And the magnon Kerr effect also can be used to create the nonreciprocal quantum entanglement via tuning the bias magnetic field direction [46]. Exploring the nonreciprocal multipartite entanglement of macroscopic objects is of great significance to the storage and transmission of information in complex quantum chiral network, but the study is still few and needs to be further supplemented.

Inspired by the above, we propose a scheme to generate the nonreciprocal macroscopic tripartite entanglement among the atomic ensemble, ferrimagnetic magnon and mechanical oscillator in a magnon-based hybrid system. In this system, the optomechanical and magnomechanical couplings are mediated by the mechanical oscillator via the magnetostrictive and radiation pressure interactions, and the optical photon in a spinning resonator couples to an ensemble of two-level atoms in the low-excitation limit. By driving the magnon with a sufficiently strong red-detuned microwave field, the magnon-phonon entanglement is initially prepared, which is partially distributed to the atom-magnon and atom-phonon subsystems when the optical photon and the atom are respectively scattered onto the two sidebands of the phonon. Specifically, the genuine tripartite entanglement among the atom, magnon, and phonon modes could be achieved, and the stationary entanglement is robust against thermal fluctuations. Moreover, the nonreciprocal bipartite and tripartite entanglements are induced by the Fizeau light-dragging effect by spinning the resonator, and the ideal nonreciprocal tripartite entanglement could be obtained by properly choosing the system parameters.

In Sect. 2, we introduce a hybrid atom-optomagnomechanical system composed of a YIG micro-bridge supporting the magnon and phonon, an spinning optical resonator, and an atomic ensemble, provide its Hamiltonian and the corresponding quantum Langevin equations (QLEs), and study the linearized dynamics of this system. In Sect. 3, we show the generation of macroscopic atom-magnon-phonon entanglement and discuss the nonreciprocity of multipartite entanglement under the influence of various system parameters. In Sect. 4, a summary is given.

2 Model and equation

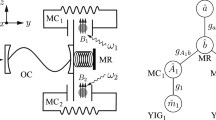
We consider a hybrid atom-optomagnomechanical system consisting of an atomic ensemble of two-level atoms, a magnon, a phonon, and an optical photon, as shown in Fig. 1(a) and 1(b). A YIG micro-bridge attached to a small high-reflectivity mirror pad on the surface and an atomic ensemble are placed in a spinning optical resonator driven by a laser field. The YIG crystal is driven by a microwave field and simultaneously in a uniform bias magnetic field along the z direction, where the magnetostriction-induced phononmode interacts with the magnon. The optical photon couples to the phonon and the atomic ensemble via the radiation-pressure [12, 13] and collective Tavis–Cummings-type interactions [47–49], respectively. The Hamiltonian of the system is given by the sum of the free term

$$\begin{aligned} H_{0}/\hbar =\omega _{m}m^{\dagger}m+\omega _{c}c^{\dagger}c+ \frac{\omega _{a}}{2}S_{z}+ \frac{\omega _{b}}{2}\bigl(q^{2}+p^{2}\bigr) \end{aligned}$$
(1)

and the interaction term

$$\begin{aligned} H_{I}/\hbar ={}&g_{a}\bigl(S_{+}c+S_{-}c^{\dagger} \bigr)+g_{m}m^{\dagger}mq-g_{c}c^{\dagger}cq+iE_{1}\bigl(m^{\dagger}e^{-i\omega _{0}t}-H.c. \bigr)+iE_{2}\bigl(c^{\dagger}e^{-i\omega _{L}t}-H.c.\bigr), \end{aligned}$$
(2)

where \(m(m^{\dagger})\) and \(c(c^{\dagger})\) are annihilation (creation) operators of the magnon and the optical photon, respectively, satisfying \([j,j^{\dagger}]=1(j=m,c)\). \(S_{z,\pm}=\sum_{i=1}^{N_{{a}}}\sigma _{z,\pm }^{i}\) are collective spin operators of an ensemble of \(N_{{a}}\) two-level atoms with Pauli matrices \(\sigma _{z,\pm}\) and satisfy the commutation relations \([S_{+},S_{-}]=S_{z}\) and \([S_{z},S_{\pm}]=\pm 2S_{\pm}\). q and p are the dimensionless position and momentum of the phonon (\([q,p]=i\hbar \)). \(\omega _{m},\omega _{c},\omega _{a}\),and \(\omega _{b}\) are resonant frequencies of the magnon, optical photon, atomic ensemble and phonon modes, respectively. The magnon frequency can be flexibly adjusted by the external bias magnetic field H, which is described as \(\omega _{m}=\gamma H\) with the gyromagnetic ratio \(\gamma /2\pi =28\) GHz/T. \(g_{a}=\mu \sqrt{\omega _{c}/2\hbar \varepsilon _{0}V_{c}}\) is the atom-photon coupling coefficient, where μ is the atomic dipole moment, \(\varepsilon _{0}\) is the vacuum conductivity, and \(V_{c}\) is the optical mode volume. \(g_{m}\) \((g_{c})\) is the single-magnon magnomechanical (single-optical optomechanical) coupling strength. The Rabi frequency [32] \(E_{1}=\frac{\sqrt{5}}{4}\gamma \sqrt{N}H_{d}\) indicates the coupling strength between the magnon and the microwave driving field with frequency \(\omega _{0}\) and amplitude \(H_{d}\), where N is the total spin number of the YIG micro-bridge. \(E_{2}=\sqrt{2\kappa _{c}P_{L}/(\hbar \omega _{L})}\) denotes the coupling strength between the optical photon and the driving laser field with frequency \(\omega _{L}\) and power \(P_{L}\), where \(\kappa _{c}\) is the optical photon decay rate. When the excitation probability of a single atom is small [50], the atom is in the low-excitation limit. In this case, all atoms are initially prepared in the ground state (\(S_{z} \simeq \langle S_{z} \rangle \simeq -N_{a}\)), and the dynamics of the atomic polarization can be described in terms of bosonic operators. The atomic annihilation operator could be defined as \(a=S_{-}/\sqrt{ \vert \langle S_{z} \rangle \vert }\), which satisfies the usual bosonic commutation relation \([a,a^{\dagger}]=1\).

Figure 1
figure 1

(a)-(b) Hybrid atom-optomagnomechanical system. An optical mode driven by a laser at frequency \(\omega _{L}\) in a spinning resonator couples to an ensemble of two-level atoms (a) and a magnon mode (m) in a YIG micro-bridge by the mediation of a phonon mode (b) induced by magnetostriction. The YIG micro-bridge is driven by a strong microwave field at frequency \(\omega _{0}\), and simultaneously is in a uniform bias magnetic field along the z direction. (c) Frequencies and linewidths of the system. When the magnon is resonant with the blue sideband (anti-Stokes) of the driven field at frequencies \(\omega _{0}+\omega _{b}\) and the optical photon and atom modes are scatted by the phonon onto two sidebands, the genuine atom-magnon-phonon entanglement is generated at the steady state. (d) By fixing the CW rotation of the resonator, we have the frequency \(\omega _{c}-\Delta _{s}\) (\(\omega _{c}+\Delta _{s}\)) for the optical CW (CCW) mode when the light is driven from the right-hand (left-hand)

Full size image

On the other hand, due to the optical Sagnac effect, the counterpropagating light would travel different effective optical path lengths by spinning the resonator. In this case, the optical photon experiences an opposite Fizeau frequency shift \(\Delta _{s}\) (\(\omega _{c} \rightarrow \omega _{c}+\Delta _{s}\)), degenerating into the clockwise (CW) and counterclockwise (CCW) modes [39, 41]. In a rotating frame with respect to \(\hbar \omega _{L}(a^{\dagger}a+c^{\dagger }c)+\hbar \omega _{0}m^{ \dagger}m\), the bosonized Hamiltonian can be written as

$$\begin{aligned} H/\hbar ={}&\Delta _{a}a^{\dagger}a+\Delta _{m}m^{\dagger}m+ \Delta _{c}c^{\dagger}c+\frac{\omega _{b}}{2} \bigl(q^{2}+p^{2}\bigr)+g_{N}\bigl(a^{\dagger}c+ac^{ \dagger } \bigr) \\ &{} +g_{m}m^{\dagger}mq-g_{c}c^{\dagger}cq+iE_{1} \bigl(m^{\dagger}-m\bigr)+iE_{2}\bigl(c^{\dagger}-c \bigr), \end{aligned}$$
(3)

where \(\Delta _{a}=\) \(\omega _{a}-\) \(\omega _{L}\), \(\Delta _{m}=\) \(\omega _{m}-\) \(\omega _{0}\), \(\Delta _{c}=\) \(\omega _{c}-\) \(\omega _{L}+ \Delta _{s}\), and \(g_{N}=g_{a}\sqrt{N}\) describes the effective atom-photon coupling strength. If the resonator is rotated in CW direction (see Fig. 1(a))) with an angular velocity Ω, the Sagnac–Fizeau shifts are [51]

$$\begin{aligned} \Delta _{s}=\pm \frac{nR\Omega \omega _{c}}{c}\biggl(1-\frac{1}{n^{2}}- \frac{\lambda}{n}\frac{\,dn}{d\lambda}\biggr), \end{aligned}$$
(4)

where \(n(R)\) is the refractive index (radius) of the resonator, \(c(\lambda )\) is the speed (wavelength) of light in vacuum, and the dispersion term \(dn/d\lambda \) is relatively small and can be ignored. \(\Delta _{s}>0\) \((\Delta _{s}<0)\) denotes that the optical CCW (CW) mode is driven from the left-hand (right-hand) side.

In the standard fluctuation-dissipation theorem, the QLEs of the system can be obtained

$$\begin{aligned} \begin{aligned} &\dot{a} =-(i\Delta _{a}+\gamma _{a})a-ig_{N}c+ \sqrt{2\gamma _{a}}a_{in}, \\ &\dot{c} =-(i\Delta _{c}+\kappa _{c})c+ig_{c}cq+E_{2}+ \sqrt{2\kappa _{c}}c_{in}, \\ &\dot{m} =-(i\Delta _{m}+\kappa _{m})m-ig_{m}mq+E_{1}+ \sqrt{2\kappa _{m}}m_{in}, \\ &\dot{q} =\omega _{b}p,\dot{p}=-\omega _{b}q-\gamma _{b}p+g_{c}c^{ \dagger }c-g_{m}m^{\dagger}m+ \xi, \end{aligned} \end{aligned}$$
(5)

where \(\gamma _{a}\), \(\kappa _{m}\), and \(\gamma _{b}\) are dissipation rates of the atomic excited level, the magnon, and the phonon, respectively. \(a_{in}\), \(c_{in}\), and \(m_{in}\) are the corresponding input noise operators with zero mean, which satisfy the following correlation functions: \(\langle j(t)j^{\dagger}(t^{\prime}) \rangle =[N_{j}( \omega _{j})+1]\delta (t-t^{\prime})\), and \(\langle j(t)^{\dagger}j(t^{\prime}) \rangle =N_{j}( \omega _{j})\delta (t-t^{\prime})(j=a,c,m)\). \(\xi (t)\) is the Hermitian Brownian noise operator, which is essentially non-Markovian. But for a large mechanical quality factor \(Q_{b}=\omega _{b}/\gamma _{b}\gg 1\) [52], the Markovian approximation can be taken, so it can be considered as a δ-autocorrelation: \(\langle \xi (t)\xi (t^{\prime})+\xi (t^{\prime})\xi (t) \rangle /2\simeq \gamma _{b}[2N_{b}(\omega _{b})+1] \delta (t-t^{\prime})\). The equilibrium mean thermal number of each mode is defined as \(N_{k}(\omega _{k})=[\exp (\hbar \omega _{k}/\kappa _{B}T)-1]^{-1}( \kappa =a,c,m,b)\), where \(\kappa _{B}\) and T are the Boltzmann constant and the environmental temperature, respectively.

By continuously driving the magnon and the optical photon with strong pumping fields, the magnomechanical and optomechanical couplings can be enhanced, which leads to large steady-state coherent amplitudes \(\vert \langle m \rangle \vert , \vert \langle c \rangle \vert \gg 1\). Therefore, the dynamics of the system can be linearized around the steady-state values by writing the operators as \(k= \langle k \rangle +\delta k\) and neglecting the second-order fluctuation terms. The quadratures of the atomic ensemble, magnon, and optical photon are defined as \(X_{j}=(j+j^{\dagger})/\sqrt{2}\) and \(Y_{j}=i(j^{\dagger}-j)/\sqrt{2}\), and similarly for the quadrature components of input noise operators \(X_{j}^{in}=(j_{in}+j_{in}^{\dagger})/\sqrt{2}\) and \(Y_{j}^{in}=i(j_{in}^{\dagger}-j_{in})/\sqrt{2}\). The linearized QLEs describing the quantum fluctuations of the system can be expressed as

$$\begin{aligned} \dot{u}(t)=Au(t)+n(t), \end{aligned}$$
(6)

where \(u(t)=[\delta X_{a}(t),\delta Y_{a}(t),\delta X_{c}(t),\delta Y_{c}(t), \delta q(t),\delta p(t),\delta X_{m}(t),\delta Y_{m}(t)]^{T}\), \(n(t)=[\sqrt{2\kappa _{a}}X_{a}^{in}, \sqrt{2\kappa _{a}}Y_{a}^{in}, \sqrt {2\kappa _{c}}X_{c}^{in},\sqrt{2\kappa _{c}}Y_{c}^{in},0,\xi (t), \sqrt {2\kappa _{m}}X_{m}^{in},\sqrt{2\kappa _{m}}Y_{m}^{in}]^{T}\) and the drift matrix A is given by

$$\begin{aligned} A= \begin{pmatrix} -\gamma _{a} & \Delta _{a} & 0 & g_{N} & 0 & 0 & 0 & 0 \\ -\Delta _{a} & -\gamma _{a} & -g_{N} & 0 & 0 & 0 & 0 & 0 \\ 0 & g_{N} & -\kappa _{c} & \tilde{\Delta}_{c} & G_{c} & 0 & 0 & 0 \\ -g_{N} & 0 & -\tilde{\Delta}_{c} & -\kappa _{c} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & \omega _{b} & 0 & 0 \\ 0 & 0 & 0 & -G_{c} & -\omega _{b} & -\gamma _{b} & 0 & G_{m} \\ 0 & 0 & 0 & 0 & -G_{m} & 0 & -\kappa _{m} & \tilde{\Delta}_{m} \\ 0 & 0 & 0 & 0 & 0 & 0 & -\tilde{\Delta}_{m} & -\kappa _{m}\end{pmatrix}. \end{aligned}$$
(7)

\(\tilde{\Delta}_{c}=\Delta _{c}-g_{c} \langle q \rangle \) \((\tilde{\Delta}_{m}=\Delta _{m}+g_{m} \langle q \rangle )\) is the effective optomechanical (magnomechanical) detuning including the frequency shift due to the radiation pressure (magnetostriction), where the mechanical displacement is \(\langle q \rangle =(g_{c} \vert \langle c \rangle \vert ^{2}-g_{m} \vert \langle m \rangle \vert ^{2})/\omega _{b}\). \(G_{m}=-i\sqrt{2}g_{m} \langle m \rangle \) and \(G_{c}=i\sqrt{2}g_{c} \langle c \rangle \) are the corresponding effective coupling strengths, where

$$\begin{aligned} \begin{aligned}&\langle m \rangle = \frac{E_{1}}{\kappa _{m}+i\tilde{\Delta}_{m}}\text{, }\\ &\langle c \rangle = \frac{E_{2}(\gamma _{a}+i\Delta _{a})}{g_{N}^{2}+(\kappa _{c}+i\tilde{\Delta}_{c})(\gamma _{a}+i\Delta _{a})}. \end{aligned} \end{aligned}$$
(8)

The average value of the atomic mode is \(\langle a \rangle =-ig_{N} \langle c \rangle /( \gamma _{a}+i\Delta _{a})\). Under the optimal conditions \(\vert \tilde{\Delta}_{m} \vert , \vert \Delta _{a} \vert , \vert \Delta _{1} \vert \simeq \omega _{b}\gg \kappa _{j}\) (see Fig. 1(c)), the average values can be simplified as \(\langle m \rangle \simeq -iE_{1}/\tilde{\Delta}_{m}\) and \(\langle c \rangle \simeq iE_{2}\Delta _{a}/(g_{N}^{2}- \tilde{\Delta }_{c}\Delta _{a})\), which are the pure imaginary numbers. Correspondingly, the effective coupling strengths \(G_{m}\) and \(G_{c}\) are approximately real numbers. If the real parts of all eigenvalues of A are negative, the system is stable and reaches a steady state when \(t\rightarrow \infty \). The steady-state conditions of system can be derived by the Routh–Hurwitz criterion [53] (i.e., \(\vert A-\lambda \mathbf{I} \vert =0\)). In this work, the characteristic equation is in the form of eighth-order polynomial for the \(8\times 8\) drift matrix A, which is difficult to solve the stability conditions analytically. Here we numerically calculate and guarantee that all parameters satisfy the stability conditions. Due to the linearized dynamics and Gaussian input noise, the system is a continuous variable (CV) four-mode Gaussian state, which can be characterized by a \(8\times 8\) covariance matrix (CM) V defined as \(V_{ij}= \langle u_{i}(t)u_{j}(t^{\prime})+u_{j}(t^{\prime})u_{i}(t) \rangle /2\) \((i,j=1,2,\ldots 8)\). The steady-state CM V can be obtained by solving the Lyapunov equation [54]

$$\begin{aligned} AV+VA^{T}=-D, \end{aligned}$$
(9)

where \(D=\operatorname{diag}[\kappa _{a}(2N_{a}+1),\kappa _{a}(2N_{a}+1),\kappa _{c}(2N_{c}+1),\kappa _{c}(2N_{c}+1),0,\gamma _{b},\kappa _{m}(2N_{m}+1), \kappa _{m}(2N_{m}+1)]\) is the diffusion matrix defined as \(\langle n_{i}(t)n_{j}(t^{\prime})+n_{j}(t^{\prime})n_{i}(t) \rangle /2=D_{ij}\delta (t-t^{\prime})\). The minimal residual contangle \(R_{\tau}^{\min}\) [55] is taken to quantify the genuine tripartite entanglement among the atomic, the magnon and the phonon, which is given by

$$\begin{aligned} R_{\tau}^{\min}\equiv \min \bigl[R_{\tau}^{a|mb},R_{\tau}^{m|ab},R_{\tau}^{b|am} \bigr], \end{aligned}$$
(10)

where \(R_{\tau}^{i|jk}\equiv C_{i|jk}-C_{i|j}-C_{i|k}\geq 0\) \((i,j,k=a,m,b)\) is the residual contangle, which is a CV analogue of tangle for discrete-variable tripartite entanglement, \(C_{u|v}\) is defined as the square of logarithmic negativity [56] of subsystems u and v (v contains one or two subsystems), namely, \(C_{u|v}=E_{u|v}^{2}\) with \(E_{N}=\max [0,-\ln (2v)]\). When v contains one mode, v= \(\min [eig|i\Omega _{2}\tilde{V}_{4}|]\) (the symplectic matrix \(\Omega _{2}=\bigoplus_{j=1}^{2}i\sigma _{y}\) and the y-Pauli matrices \(\sigma _{y}\)), \(\tilde{V}_{4}=P_{12}V_{4}P_{12}\), \(P_{12}=\operatorname{diag}[1,-1,1,1]\) (the martix that implements partial transposition at the level of \(CMs\)) and \(V_{4}\) is the \(4\times 4\) CM of the two modes. When v contains two modes, for calculation the logarithmic negativity \(E_{i|jk}\), one only needs to follow the definition by replacing \(\Omega _{2}=i\sigma _{y}\oplus i\sigma _{y}\) with \(\Omega _{3}=i\sigma _{y}\oplus i\sigma _{y}\) ⊕ \(i\sigma _{y}\), and \(\tilde{V}_{4}=P_{12}V_{4}P_{12}\) with \(\tilde{V}_{6}=P_{i|jk}V_{6}P_{i|jk}\), where \(P_{1|23}=\operatorname{diag}[1,-1,1,1,1,1],P_{2|13}=\operatorname{diag}[1,1,1,-1,1,1],P_{3|12}=\operatorname{diag}[1,1,1,1,1,-1]\) are partial transposition matrices. The residual contangle satisfies the monogamy inequality, thus when \(R_{\tau}^{\min}>0\), the corresponding genuine tripartite entanglement is present in the system.

3 Results and discussion

We numerically calculate the bipartite and tripartite entanglements among three of modes atom ensemble, magnon and phonon versus detunings \(\tilde{\Delta }_{m}\) and \(\Delta _{a}\) for the case \(\Omega =0\) at the steady state, which are shown in Fig. 2. Here the static system has reciprocity regardless of the driving direction. The experimentally feasible parameters are taken as [12, 13, 32] \(\omega _{m}/2\pi =10\) GHz, \(\omega _{b}/2\pi =25\) MHz, \(\lambda _{c}=1550\) nm, \(\gamma _{a}/2\pi =\) \(\kappa _{m}/2\pi =1\) MHz, \(\gamma _{b}/2\pi =100\) Hz, \(\kappa _{c}/2\pi =1.5\) MHz, \(g_{N}/2\pi =16\) MHz, \(G_{m}/2\pi =8\) MHz, \(G_{c}/2\pi =3\) MHz, \(g_{c}/2\pi =1\) kHz, \(T=10\) mK, and the atom ensemble is tuned to off-resonant coupling with the optical photon (\(\Delta _{a}=-\tilde{\Delta}_{c}\)). The effective magnomechanical coupling \(G_{m}/2\pi =8\) MHz corresponds to a microwave drive power \(P_{0}\simeq 1.44\) mW for a \(8\times 3\times 1\) μm3 YIG micro-bridge with \(g_{m}/2\pi =25\) Hz [14]. From Fig. 2(a), 2(b) and 2(c), it can be found that all bipartite entanglements among the atom, magnon and phonon modes can coexist in the parameters regime around \(\tilde{\Delta}_{m}\simeq \omega _{b}\) and \(\Delta _{a}\simeq -\omega _{b}\). Interestingly, the genuine tripartite entanglement of the three modes could be achieved at steady state, which is demonstrated by the minimum residual contangle \(R_{\tau}^{\min}\) greater than zero in Fig. 2 (d). The similar mechanism has been demonstrated to achieve the genuine atom-light-mirror entanglement in cavity optomechanics and magnon-photon-phonon entanglement in cavity magnomechanics, respectively [32, 50]. Different from that, our work combines the respective advantages of the two systems, and further prepares the macroscopic tripartite entanglement among the atomic ensemble, massive ferrimagnetic magnon and mechanical oscillator based on the cooperative effect of magnetostrictive and radiation-pressure interactions.

Figure 2
figure 2

Density plot of logarithmic negativity related to bipartite entanglement (a) \(E_{mb}\), (b) \(E_{ab}\), (c) \(E_{am}\), and (d) tripartite atom-magnon-phonon entanglement \(R_{\tau}^{\min}\) versus detunings \(\tilde{\Delta}_{m}\) and \(\Delta _{a}\) with \(\tilde{\Delta}_{c}=-\Delta _{a}\) and \(\Omega =0\). See text for the other parameters.

Full size image

Figure 3 shows the influence of the effective optical detuning, thermal fluctuations and mechanical damping on the bipartite and tripartite entanglements among the atom, magnon and phonon modes in the static system (\(\Omega =0\)). In Fig. 3(a), three bipartite entanglements interplay with each other and the degree of entanglements could be controlled by detuning \(\tilde{\Delta}_{c}\). It can be seen that the variation trend of magnon-phonon (blue dashed) entanglement with detuning \(\tilde{\Delta}_{c}\) is opposite to that of the atom-magnon (black dot-dashed) and atom-phonon (red solid) entanglements. This indicates that the magnon-phonon entanglement originally prepared in the magnomechanical system is used as a quantum resource, which is partially distributed to the atom-phonon and atom-magnon subsystems, thus yielding a genuinely macroscopic tripartite entangled state in the hybrid system. The tripartite entanglement in terms of the minimum residual contangle \(R_{\tau}^{\min}\) versus \(\tilde{\Delta}_{c}\) is illustrated in Fig. 3(b). It can be found that the atom-magnon-phonon entanglement is sensitive to detuning \(\tilde{\Delta}_{c}\), and the maximum tripartite entanglement can reach 0.037 at \(\tilde{\Delta}_{c}=0.5\omega _{b}\). Figure 3(c) shows the bipartite and tripartite entanglements under the effect of ambient temperature with optimized \(\tilde{\Delta}_{c}\). We can see that all entanglements are degraded by the increase of thermal fluctuations. The macroscopic tripartite entanglement can survive up to \(T\simeq 210\) mK, and the atom-magnon and atom-phonon entanglement even exist for bath temperature over 350 mK. Due to the attachment of a mirror on the surface of YIG bridge, an additional mechanical damping of the phonon is inevitably introduced. The steady-state entanglements versus the mechanical damping \(\gamma _{b}\) with optimal \(\tilde{\Delta}_{c}\) are shown in Fig. 3(d). It is obvious that the entanglement remains almost constant with the increase of damping rate to \(\gamma _{b}/2\pi \sim 5\times 10^{3}\) Hz, and the macroscopic tripartite entanglement is still present with a large damping rate \(\gamma _{b}/2\pi \sim 5\times 10^{4}\) Hz.

Figure 3
figure 3

(a) Bipartite entanglement \(E_{mb}\), \(E_{ab}\), and \(E_{am}\) and (b) tripartite entanglement \(R_{\tau}^{\min}\) versus detuning \(\tilde{\Delta}_{c}\). Bipartite and tripartite entanglement versus (c) temperature T and (d) mechanical damping rate \(\gamma _{b}\) where \(\tilde{\Delta}_{c}\) is optimized for each entanglement, respectively. The other parameters are the same as in Fig. 2

Full size image

It is essential to elucidate the mechanism for generating macroscopic tripartite entanglement in such quadripartite compound hybrid system with large frequency mismatch. For this purpose, we proceed via the linearized Hamiltonian of the static system (\(\Omega =0\)) for quantum fluctuations

$$\begin{aligned} H_{lin} ={}&\Delta _{a}\delta a^{\dagger}\delta a+\tilde{ \Delta}_{m} \delta m^{\dagger}\delta m+\tilde{\Delta}_{c} \delta c^{\dagger} \delta c+\omega _{b}\delta b^{\dagger}\delta b+g_{N}\bigl(\delta a^{ \dagger}\delta c+\delta a\delta c^{\dagger}\bigr) \\ &{} +\bigl[G_{m}^{\prime}\bigl(\delta m^{\dagger}\delta b+ \delta m\delta b\bigr)-G_{c}^{\prime}\bigl(\delta c^{\dagger}\delta b+\delta c\delta b\bigr)+H.c.\bigr], \end{aligned}$$
(11)

where \(\delta b=(\delta q+i\delta p)/\sqrt{2}\), \(G_{m}^{\prime}=G_{m}/\sqrt {2}\), and \(G_{c}^{\prime}=G_{c}/\sqrt{2}\). When the magnon is driven by a sufficiently strong red-detuned microwave field (\(\tilde{\Delta}_{m}\simeq \omega _{b}\)), the magnomechanical anti-Stokes scattering is activated and the strong magnomechanical coupling (\(G_{m}/2\pi =8\) MHz) that breaks the weak coupling condition (\(G_{m}\ll \omega _{b}\)) of the rotating-wave (RW) approximation. In this case, the magnomechanical RW term ∝ \(\delta m^{\dagger}\delta b+\delta m\delta b^{\dagger}\) and the optomechanical coupling \(\delta c^{\dagger}\delta b+\delta c\delta b^{\dagger}\) (the weak optomechanical coupling strength satisfies the RW approximation condition for the optical photon driven by a red-detuned laser field) are linear beam-splitter interactions, which can significantly cool the low-frequency mechanical mode (∼MHz) in the resolved sideband limit (\(\omega _{b}\gg \kappa _{m}, \kappa _{c}\)). The heat of phonon thermal excitation can be eventually dissipated to the environment through magnon and photon decay. The counter-RW term ∝ \(\delta m^{\dagger}\delta b^{\dagger }+\delta m\delta b\) corresponding to the parametric down-conversion interaction, which plays an important role in generating the magnon-phonon entanglement. When the optical and atom modes are scattered by the mechanical vibration onto the two sidebands (\(\Delta _{a}=-\tilde{\Delta}_{c}\), see Fig. 1(c)), the magnon-phonon entanglement is partially distributed to the atom-phonon and atom-magnon subsystems through the atom-photon and optomechanical state exchange interactions, realizing a genuinely tripartite entangled state in the system.

Then we show that the classical nonreciprocity of mean optical photon number and quantum nonreciprocity of macroscopic entanglements can be observed by spinning the resonator. Here we adopt the angular velocity \(\Omega =20\) KHz and the resonator with \(n=1.48\) and \(R=1.1\) mm, which are feasible in the current experimental technology [41, 51]. Due to the optical Sagnac effect, the frequency of the optical photon driven from the left-hand (right-hand) side experiences a blue (red) shift \(\Delta _{s}>0\) (\(\Delta _{s}<0\)) (see Fig. 1(d)) in the spinning resonator. Accordingly, the effective optomechanical detuning (\(\tilde{\Delta}_{c}=\omega _{c}-\omega _{L}+ \Delta _{s}-g_{c} \langle q \rangle \)) are different for the CW and CCW modes. And the mean optical photon number exhibits nonreciprocity (\(\vert \langle c(\Delta _{s}>0) \rangle \vert ^{2}\neq \vert \langle c(\Delta _{s}<0) \rangle \vert ^{2}\)) for the same driving field pump power in opposite directions, which is demonstrated in Fig. 4(a). Furthermore, the optomechanical coupling strength (\(G_{c}=\sqrt{2}g_{c} \langle c \rangle \)) and the average value \(\langle q \rangle =(g_{c} \vert \langle c \rangle \vert ^{2}-g_{m} \vert \langle m \rangle \vert ^{2})/\omega _{b}\) are also affected, which leads to the irreversibility of entanglement when the optical photon is driven in opposite directions. The stationary nonreciprocal bipartite entanglements versus detuning \(\tilde{\Delta}_{c}\) are respectively shown in Fig. 4(b), 4(c), and 4(d). Taking the atom-magnon entanglement in Fig. 4(d) as an example, it can be seen that the atomic ensemble and magnon are strongly entangled at \(\tilde{\Delta}_{c}=\omega _{b}\) when the optical photon is driven in CW (\(\Delta _{s}<0\)), yet fully separated in the opposite driving direction (\(\Delta _{s}>0\)).

Figure 4
figure 4

(a) Mean optical photon number \(\vert \langle c \rangle \vert ^{2}\) versus detuning \(\tilde{\Delta}_{c}\) with \(\Delta _{a}=-0.5\omega _{b}\) in the presence of the spinning. Nonreciprocal bipartite entanglement (b) \(E_{mb}\), (c) \(E_{ab}\), and (d) \(E_{am}\) versus detuning \(\tilde{\Delta}_{c}\) with \(\Delta _{a}=-\tilde{\Delta}_{c}\). We take \(\tilde{\Delta}_{m}=\omega _{b}\) and \(\Omega =20\) KHz in all plots. The other parameters are the same as in Fig. 2

Full size image

The macroscopic tripartite entanglement among the atomic ensemble, ferrimagnetic magnon and mechanical oscillator also inherits the nonreciprocal property, which is depicted in Fig. 5(a). It is evident that the tripartite entanglement is the strongest at \(\tilde{\Delta}_{c}=0.5\omega _{b}\) without spinning (black dashed). When the resonator is selectively rotated, the maximum of tripartite entanglement is generated at \(\tilde{\Delta}_{c}=\omega _{b}\) by driving the optical photon from the right-hand side (\(\Delta _{s}<0\)) but disappears from the left-hand side (\(\Delta _{s}>0\)) at the same conditions, which realizes the nonreciprocal macroscopic tripartite entanglement at steady state. Figure 5(b) shows the nonreciprocal tripartite entanglement versus temperature with \(\tilde{\Delta}_{c}=\omega _{b}\). It could be found that the tripartite entanglement is damped by thermal fluctuations without the spinning, but which could be strongly enhanced by rotating the resonator with the appropriate driving direction of laser field. The tripartite entanglement versus the rotation speed Ω with \(\tilde{\Delta}_{c}=0.95\omega _{b}\) for the opposite driving direction \(\Delta _{s}>0\) or \(\Delta _{s}<0\) is illustrated in Fig. 5(c). Obviously, once the optical resonator is rotated, the nonreciprocity of the atom-magnon-phonon entanglement would appear. As the rotation speed increases, the tripartite entanglement is gradually weakened for \(\Delta _{s}>0\), but the entanglement could be significantly enhanced for \(\Delta _{s}<0\).

Figure 5
figure 5

Nonreciprocal tripartite entanglement \(R_{\tau}^{\min}\) (a) versus detuning \(\tilde{\Delta}_{c}\), the temperature T with \(\tilde{\Delta}_{c}=1.4\omega _{b}\), and (c) the rotation speed Ω with \(\tilde{\Delta }_{c}=0.95\omega _{b}\). (d) The chiral factor χ of atom-magnon-phonon entanglement as a function of detuning \(\tilde{\Delta}_{c}\) and rotation speed Ω. The other parameters are the same as in Fig. 2

Full size image

In order to further study the nonreciprocity of macroscopic atom-magnon-phonon entanglement, the chiral factor is chosen to quantify, which is defined as

$$\begin{aligned} \chi = \biggl\vert \frac{R_{\tau}^{\min}(\Delta _{s}>0)-R_{\tau}^{\min}(\Delta _{s}< 0)}{R_{\tau}^{\min}(\Delta _{s}>0)+R_{\tau}^{\min}(\Delta _{s}< 0)} \biggr\vert . \end{aligned}$$
(12)

The chiral factor \(\chi >0\) (\(\chi \leq 1\)) denotes that the nonreciprocity of tripartite entanglement is present. Figure 5(d) shows the chiral factor versus detuning \(\tilde{\Delta}_{c}\) and rotation speed Ω. It can be found that the tripartite entanglement is reciprocal (\(\chi =0\)) without the spinning of the resonator \(\Omega =0\). However, the nonreciprocal tripartite entanglement appears by spinning the resonator, and the nonreciprocity of entanglement can be flexibly implemented by the optical detuning and rotating speed of the resonator. The nearly ideal macroscopic nonreciprocal tripartite entanglement could be obtained (\(\chi =1\)) in the steady-state system.

Finally, we discuss the validity of the system and the detection of nonreciprocal entanglement. The above results are valid only when atom and magnon are in low-lying excitations. When the single-atom excitation probability \(P_{a}=g_{a}^{2} \vert \langle a \rangle \vert ^{2}/(\Delta _{a}^{2}+\gamma _{a}^{2})\) is much smaller than 1 and \(\langle a^{\dagger}a \rangle \ll N_{a}\), the atomic polarization can be described by boson operators. In this paper, we obtain \(\langle a^{\dagger}a \rangle = \vert \langle a \rangle \vert ^{2}\sim 10^{6}\ll N_{a}\sim 10^{7}\) with \(g_{a}/2\pi =2\times 10^{3}\) Hz [50] and \(\vert \Delta _{a} \vert \simeq \omega _{b}\), which satisfies \(P_{a}\sim 0.006\ll 1\). For the magnon, \(\langle m^{\dagger}m \rangle =5.1\times 10^{10}\ll 5N=5.1 \times 10^{11}\), which meets the low-excitation condition. The steady-state entanglement properties can be verified by experimentally measuring the corresponding CMs using homodyne techniques (see Ref. [22, 54]). A weak microwave (optical) probe field is sent to resonantly couple to the magnon (atomic ensemble), thus the magnon (atomic polarization) quadratures can be read out by homodyning the microwave (optical) cavity output. The mechanical quadratures can be measured by adjusting the detuning and bandwidth of an adjacent optical cavity, both the position and momentum of the harmonic oscillator can be measured by homodyning the output of this second cavity. Once the quadratures of atomic ensemble, magnon and mechanical phonon are obtained, the nonreciprocal bipartite and tripartite entanglements could be calculated.

4 Conclusion

In conclusion, we present an approach to create and manipulate the nonreciprocal macroscopic atom-magnon-phonon entanglement in a hybrid atom-optomagnomechanical system composed of an ensemble of two-level atoms, a YIG micro-bridge, and a spinning optical resonator driven by a laser field. It is found that the atom, magnon, and phonon modes can be simultaneously entangled with each other by appropriately driving the magnon and photon, and the genuine tripartite entangled state of the three modes is generated with the feasible parameters. Furthermore, the atom-magnon-phonon entanglement depending on the optical detuning could be enhanced in a chosen direction but strongly suppressed in another direction by spinning the resonator. The stationary nonreciprocal macroscopic entanglement is robust against thermal fluctuations and could be flexibly manipulated by the spinning speed, size and structure of the resonator, optomechanical and magnomechanical coupling strength, dissipations and detunings of optical, microwave, and magnon modes. The nonreciprocal multipartite entanglement among macroscopic objects in the magnon-based hybrid system may have practical applications in quantum information processing, quantum network construction and quantum chiral device integration.