1 Introduction

Glasses have found numerous applications in various fields, such as medical imaging, nuclear power plants, space exploration, and nuclear waste storage.

As the power of ionization in many applications grows, so does the need for effective radiation-resistant materials. Traditional materials like concrete and lead have limitations, prompting researchers to explore new material compositions for radiation shielding. With its unique transparency that allows monitoring of activity from the outside, Glass has emerged as an up-and-coming candidate. The current focus is on developing high-density glass shields that are transparent enough to replace conventional shielding materials like lead, ceramics, polymers, alloys, and concrete. The composition of Glass, in specific applications, significantly influences its performance.

In medical imaging, glasses can shield patients and healthcare workers from radiation during X-ray or CT scans. In nuclear power plants, glasses can protect workers from radiation exposure, while in space exploration, glasses can safeguard astronauts from cosmic radiation. Furthermore, glasses can immobilize and contain radioactive materials in nuclear waste storage.

Transition metals such as Ni-doped glass systems, which are based on boron oxide, have found interest as a suitable material in many areas of application, such as bright windows, optical filters, gas sensors, and cells from solid oxide fuel [1] Ni-doped boron oxide glasses have been used in smart windows, where the tint of the glass can be adjusted based on the level of sunlight, helping to regulate temperature and energy consumption. These glasses have also been used in optical filters, where their ability to absorb light selectively can be used to filter out specific wavelengths. When a transition metal ion in a lower oxidation state is introduced into a glass system, it can transfer electrons to other ions in a higher oxidation state. This transfer of electrons can lead to changes in the optical properties of the glass, such as changes in color, refractive index, and absorption properties. This behavior is known as electro-optical behavior and is the basis for many applications of transition metal-doped glass. [2,3,4,5,6]. According to reference [7], NiO-containing glasses are known for their optical density, chemical stability, and durability. NiO, located within the glass matrix and modified by its ability to alter the glass network, can add color in small quantities to the host glass. It is worth noting that Ni ions can occupy tetrahedral and octahedral positions within the glass matrix [8,9,10,11].

Ultrasonic techniques have become an essential tool for investigating the mechanical properties of glass samples. Ultrasonic waves are mechanical waves propagating through a medium, traveling slower than electromagnetic waves. This slower propagation allows more detailed information to be collected about the properties of the medium. The unique advantage of ultrasonic techniques in studying glass samples lies in their ability to penetrate even opaque materials. Regardless of the transparency of the glass, ultrasonic waves can delve into the material, revealing crucial information about its mechanical properties. Moreover, the compactness and homogeneity of glass samples make them ideal for studying the propagation of ultrasonic waves. Therefore, the matrices can be used for optical, thermal, electrical, and mechanical applications [12]. Glass samples show good compactness and homogeneity compared with ceramics, polymers, and other material types; therefore, ultrasonic longitudinal and shear waves travel freely inside glass samples.

Studies have shown that adding nickel to borate-based glasses can increase their density and adequate atomic number, making them more effective in shielding against gamma and X-ray radiation. Adding nickel also improves the glass's mechanical strength and thermal stability [13,14,15,16]. It can be used in radiation protection as an alternate shielding material for concretes and polymers. Glasses are commonly used in the medical field to shield against X/gamma-radiation, alpha particles, and neutrons. Selecting a suitable glass structure depends on several radiation shielding parameters, including μm, HVL, MFP, and Zeff. The PHITS code [17] and Phy/X software can theoretically calculate these parameters. [18,19,20].

Several studies have investigated the role of these parameters in determining the optimal glass structure for radiation shielding. Some researchers have shown how to introduce transitional elements, such as nickel oxide, to some borate-based glasses' structural and optical aspects and shielding properties. So, in the present study, we focus on ultrasonic, optical, and radiation shielding behaviors of potassium lead borate glasses. In addition, to determine the mechanical properties and performance of protectors, we need to pay attention to the concentration of NiO. The densities of the samples were calculated for these glasses, and using Phy/X software and the PHITS code program to calculate radiation interaction parameters, we report the Gamma-ray shielding parameters such as μm, HVL, MFP, and Zeff. The results of this study will contribute to the development of effective radiation-shielding glasses for various applications.

2 Materials and methods

The glass system (60 − x) B2O3–20 K2O–20 PbO–x NiO, coded as xNiO, and x = (0, 2, 4, 8 and 10 mol%). The raw substances from El-Gomhouria Company were used to prepare the glasses: H3BO3, K2CO3, PbO, and NiO. Five batches were exactly weighed using a sensitive balance (four digits ± 0.0001). The batches were differentiated carefully and ground into sufficient powders to be melted in porcelain crucibles in an electric muffle furnace at 1050 °C for 30 min. The mixture was stirred frequently through the melting route to release the bubbles. After the complete melting, the homogenized melts were cast on heated stainless-steel molds and immediately transmitted to an annealing furnace at 350 °C for 3 h in another electrical furnace. Lastly, the furnace temperature was lowered progressively to reach the ambient temperature.

$${\text{2H}}_{{3}} {\text{BO}}_{{3}} + {\text{K}}_{{2}} {\text{CO}}_{{3}} + {\text{PbO}} + {\text{NiO}}\frac{{\Delta \;{\text{at}}\;{ }1050\;^{ \circ } {\text{C}}}}{{{\text{3 H}}_{{2}} {\text{O }} \uparrow + {\text{ CO}}_{{2}} \uparrow )}}\left[ {{\text{B}}_{{2}} {\text{O}}_{{3}} + {\text{K}}_{{2}} {\text{O}} + {\text{PbO}} + {\text{NiO}}} \right]$$

X-ray diffraction analysis can ascertain the amorphous or crystalline nature of a material. Using [Shimadzu X-ray diffractometer,600, forty kV and 15 mA], having copper-Kα target with 2θ = 10°–90°, θ being the Bragg’s angle were used to collect data, as well as an X-ray tube. The ultrasonic longitudinal and shear wave transit times (t) inside the glass samples were measured using a through-transmission technique. The (t) was measured on a flaw detector (Krautkramer USN 60 flaw detector). Two 4 MHz longitudinal wave transducers were used to measure the longitudinal wave transit time (tl), and Two 2 MHz shear wave transducers were used to measure the shear wave transit time (ts). Thus, the longitudinal velocity (Vl) and shear velocity (Vs) may be determined by dividing the sample thickness by the transit time. Each measurement was performed three times at room temperature. Vibrational spectra were recorded with A Bruker's VERTEX seventy Spectrometer (Model: FT/IR 70) in 400–4000 cm−1 region. To analyze the optical properties of the samples, absorbance and reflectance were analyzed at (RT) room temperature using a double beam UV/VIS/NIR spectrophotometer (JASCO model V750 Japan).

3 Theory/calculations

3.1 Ultrasonic properties

The mechanical properties of B2O3–K2O–PbO glasses filled with varying concentrations of NiO were investigated. The elastic moduli (longitudinal (L), shear (G), Young’s (E), and bulk (K)), Poisson’s ratio (σ), and microhardness (H) were calculated using the following equations [21,22,23,24,25,26,27]:

$$L\;({\text{GPa}}) = \rho V_{{\text{l}}}^{2}$$
(1)
$$G\;({\text{GPa}}) = \rho V_{{\text{s}}}^{2}$$
(2)
$$K\;({\text{GPa}}) = L - \left( \frac{4G}{3} \right)$$
(3)
$$E\;({\text{GPa}}) = \left( {1 + \sigma } \right)2G$$
(4)
$$\sigma = {\frac{{\left( {L - 2G} \right)}}{{2\left( {L - G} \right)}}}$$
(5)
$$H\;({\text{GPa}}) = { }\frac{(1 - 2\sigma)E}{{6\left( {1 + \sigma} \right)}}$$
(6)

3.2 FTIR spectra

Infrared spectra of deconvoluted FTIR bands were based on the ratio of BO4 to BO3 absorption peaks (N4 and N3, respectively) and the fraction of four coordinated boron atoms (N4). Moreover, the area of the deconvoluted bands indicates variation in N4 [28, 29]. Here are the formulas for calculating the tetrahedral boron atom fractions N4 and N3:

$${\text{N4 }} = \frac{{{\text{con}}\;{\text{of}}\;{\text{BO}}4}}{{{\text{con}}\;{\text{of}}\;{\text{BO}}4 + {\text{concentration}}\;{\text{of}}\;{\text{BO}}3}}$$
(7)
$${\text{N3}} = \frac{{{\text{con}}\;{\text{of}}\;{\text{BO}}3}}{{{\text{con}}\;{\text{of}}\;{\text{BO}}4 + {\text{concentration}}\;{\text{of}}\;{\text{BO}}3}}$$
(8)

Here are the formulas for calculating the N4 and N3 tetrahedral fractions of boron.

3.3 UV–Vis spectra

The optical reflectance (R) and the extinction coefficient (Ko) have been employed to define the linear refractive index (n) for the un-doped and NiO-doped samples as shown in the Fresnel’s expression [30, 31]

$$n = \frac{{\left( {1 + R} \right)}}{{\left( {1 - R} \right)}} + \sqrt {\frac{4R}{{\left( {1 - R} \right)^{2} }} - K^{2} }$$
(9)

3.4 Dielectric study

The optical conductivity (σopt) is possible to calculate the optical conductivity of the undoped and doped-NiO samples according to the following expression [32]

$$\sigma_{{{\text{opt}}}} = \frac{\alpha nc}{{4\pi }}$$
(10)

In the transparent area (λ > 800 nm), the refractive index (n) gives a normal dispersion behavior for all samples. Therefore, the refractive index is determined utilizing the single oscillator paradigm, which has been proposed by Wemple and DiDomenico [33, 34]

$$\frac{1}{{n^{2} - 1}} = \frac{{E_{{\text{o}}} }}{{E_{{\text{d}}} }} - \frac{1}{{E_{{\text{o}}} { }E_{{\text{d}}} }}\left( {h{\upnu }} \right)^{2}$$
(11)

where Eo is the single oscillator energy, which is assigned to the band gap energy and Ed denotes the dispersion energy which is used to conclude the strength of inter-band optical transitions.

The static refractive index values (no) can be calculated of the non-doped and doped samples using the following equation [35]:

$$n_{{\text{o}}} = \left( {1 + \frac{{E_{{\text{d}}} }}{{E_{{\text{O}}} }}} \right)^{1/2}$$
(12)

Additionally, other parameters could be calculated such as the lattice dielectric constant (εl) and the ratio between a concentration of free carrier and its effective mass (N/m*) using the Spitzer–Fan model. [36]:

$$\varepsilon_{{\text{r}}} = \varepsilon_{{\text{l}}} - \left( {\frac{{e^{2} }}{{4{ }\pi^{2} \varepsilon_{{\text{s}}} c^{2} { }}}\frac{N}{{m^{*} }}} \right)\lambda^{2} { }$$
(13)

where εr is the real part of dielectric constant, c represents the light speed, e refers to the charge of an electron, and εs indicates the free-space dielectric.

Further, the plasma resonance frequency (Wp) values of the pristine and doped-NiO samples were computed employing the following equation, [37]:

$$W_{{\text{p}}} = \frac{{e^{2} }}{{\varepsilon_{{\text{o}}} }}x\frac{N}{{m^{*} }}{ }$$
(14)

Besides, the long-wavelength refractive indices (n∞) and medium oscillator wave longitude (λo) of the non-doped and doped-NiO samples have been calculated by analyzing the refractive index data utilizing the single term Sellmeier oscillator as follows:

$${{(n_{\infty }^{2} - 1)} \mathord{\left/ {\vphantom {{(n_{\infty }^{2} - 1)} {\left( {n^{2} - 1} \right)}}} \right. \kern-0pt} {\left( {n^{2} - 1} \right)}} = 1 - \left( {\frac{{\lambda_{{\text{o}}} }}{\lambda }} \right)^{2}$$
(15)

Moreover, values of oscillator length intensity (So) have been deduced applying the following formula) [38]:

$$S_{{\text{o}}} = (n_{\infty }^{2} - 1)/(\lambda_{{\text{o}}} )^{2}$$
(16)

Nonlinear optical response of materials is distinguished by the following relation [39]:

$$P = X^{\left( 1 \right)} E + {\text{X}}^{\left( 2 \right)} E^{2} + {\text{X}}^{\left( 3 \right)} E^{3}$$
(17)

where P represents the polarization of the substance, X(1) refers to the linear susceptibility, X(2) is the second-order nonlinear susceptibility that corresponds to second harmonic generation, and X(3) represents the third-order nonlinear susceptibility. In which, \(X\)(1) and \(X\)(3) have been calculated using the following formula [40,41,42]:

$$X^{\left( 1 \right)} = \frac{{\left( {n^{2} - 1} \right)}}{4\pi }{ }$$
(18)
$$X^{\left( 3 \right)} = A\left( {X^{\left( 1 \right)} } \right)^{4} { }$$
(19)

Hence A value is constant ~ 1.7 × 10–10 for χ(3) in esu. Meanwhile, the refractive index is given in the following formula [43]:

$$n\left( \lambda \right) = n_{{\text{o}}} \left( \lambda \right) + n_{2} \left( {E^{2} } \right)$$
(20)

where no is the linear refractive index, n2 denotes the NLO refractive index. Moreover, the nonlinear refractive index (n2) of the examined samples has been evaluated by applying Ticha and Tichy, and Miller's rule. [44]

$$n_{2} = \frac{{12\pi X^{\left( 3 \right)} }}{{n_{{\text{o}}} }}$$
(21)

where no = n, because no >> n2.

The average boron–boron separation <dB–B> , Ni+ ion concentration (N), polaron radius (rp) and internuclear distance (ri) should be noted to understand the effect of NiO doping to the structure changes in glass system, While these values are calculated based in the following mathematical relations [45, 46].

$$\left\langle {d_{{{\text{B}} - {\text{B}}}} } \right\rangle \,({\text{\AA}}) = \left( {V_{M}^{B} /N_{{\text{A}}} } \right)^{1/3}$$
(22)
$$N\;\left( {\frac{{{\text{ions}}}}{{{\text{cm}}^{3} }}} \right){ } = { }\frac{{\left( {{\text{mol\% }}\;{\text{of}}\;{\text{NiO}}} \right) \times N_{{\text{A}}} \times \rho }}{{\left( {{\text{sample}}\;{\text{average}}\;{\text{molecular}}\;{\text{weight}}} \right)}}$$
(23)
$$r_{{\text{p}}} { }\left( {\text{\AA}} \right){ } = { }0.5\left( {\frac{\pi }{6N}} \right)^{1/3}$$
(24)
$$r_{{\text{i}}} { }\left( {\text{\AA}} \right){ } = { }\left( \frac{1}{N} \right)^{1/3}$$
(25)

where \(V_{M}^{B} = V_{M} /2(1 - x_{{\text{B}}} )\) is the borate glass volume which accommodate a mole of B atoms, xB is the molar fraction of the boron oxide and NA is the Avogadro’s number (6.0221 × 1023 mol−1) [25].

3.5 Shielding parameters

Phy/X software and the PHITS code program were used to calculate radiation interaction parameters for the prepared glasses. Geometrical of transmitted narrow beam transmission was simulated in order to investigate coefficients of photon attenuation of glasses under study. A schematic geometry simulation of PHITS code is shown in Fig. 1. A various glass compositions were placed among source of radiation and detector. The disk source is defined with 0.5 cm diameter that emits radiation along primary axis of cylinder. The NaI crystal (used as a detector) is considered in this simulation, with 70.62 mm height in crystal and 70.62 mm diameter. µm was used for estimation of the incident and transmitted photon intensities for each sample for settled fixed duration to determine whether it is likely that these new prepared glass systems will be used as γ ray shielding. Other shielding parameters such µL & MFP were calculated [2, 12, 18, 25], in which:

$$I = I_{o} e^{{ - \mu_{{\text{m}}} x{ }}}$$
(26)

where Io and I are, respectively, the un-attenuated and the attenuated intensities, x is the thickness of shield material. The density-independent µm can be calculated by [47]:

$$\mu_{{\text{m }}} = \frac{{\mu_{{\text{l }}} }}{\rho } = \frac{1}{\rho x}\ln \frac{{I_{o} }}{I}$$
(27)

where µL (cm–1) is the linear attenuation coefficient and ρ (g/cm3) is the material density. HVL can be calculated using the following equation [48];

$${\text{HVL}} = \frac{0.693}{{\mu_{{\text{l }}} }}$$
(28)
Fig. 1:
figure 1

3D view of the simulation geometry designed by PHITS code

Full size image

In addition, MFP of the glass can be calculated as following:

$${\text{MFP}} = \frac{1}{{\mu_{{\text{l}}} }}$$
(29)

The average atomic cross section, σt,a (barn/atom) can be calculated as [49];

$$\sigma_{{{\text{t}},{\text{a}}}} = \frac{{\mu_{{\text{m}}} M}}{{N_{{\text{A}}} \mathop \sum \nolimits_{i} n_{i} }}$$
(30)

where \(M = \mathop \sum \limits_{i} n_{i} A_{i}\) is the molar mass, NA is Avogadro's constant, ni is the number of atoms of the element i having atomic weight Ai. And the average electronic cross section, σt, el (barn/atom) is given by [49];

$$\sigma_{{{\text{t}},{\text{el}}}} = \frac{1}{{N_{{\text{A}}} }} \mathop \sum \limits_{i}^{n} \frac{{f_{i} A_{i} (\mu_{{\text{m}}} )_{i} }}{{Z_{i} }}$$
(31)

where \(f_{i}\) = ni/∑ni is the ratio of number of atoms of the element i to the total number of atoms present in the formula and Zi is the atomic number of the element i. When describing the shielding characteristics of composites in terms of pure elements, the Zeff, is gamma ray interaction parameter and it is obtained utilizing Eq. (32) [48, 50];

$$Z_{{{\text{eff}}}} = \frac{{\sigma_{{{\text{t}},{\text{A}}}} }}{{\sigma_{{{\text{t}},{\text{el}}}} }}$$
(32)

4 Results and discussion

4.1 X-ray diffraction (XRD

Figure 2 displays the XRD patterns of the investigated glasses, where broad hump peaks appeared and no crystalline peaks were detected, indicating the notably amorphous natures of the samples and then their glassy states.

Fig. 2
figure 2

The XRD patterns of the samples

Full size image

4.2 Ultrasonic properties

It has been found that the ultrasonic elastic moduli, Poisson’s ratio, and microhardness were determined based on the measured ultrasonic longitudinal and shear wave velocities (Vl and Vs) and the sample densities (ρ), which are listed in Table 1. Fig. 3 represent the variation of longitudinal, shear, Young’s, and bulk moduli with NiO content for the NiO doped B2O3–K2O–PbO glasses. The L, G, and E recorded 60.87, 17.15, and 44.72 GPa for the sample with x = 0. Modifying the glass system with NiO at x = 2 mol%, the same moduli recorded 52.73, 17.01, and 42.94 GPa and increased steadily to record the maximum values of 59.77, 19.21, and 48.53 GPa for the sample with x = 10 mol%. Unlike the K and σ, they recorded their maximum values of 35.78 GPa and 0.29, respectively, at x = 8 mol% and then decreased. The increased trend indicates the modification of the glass rigidity, which is in agreement with the density and bond length constants [44]. This is mainly because the Ni+2 ions replace some B ions and fill interstitially in the borate glass network. Moreover, the increase could be ascribed to the rise of the anti-harmonic electron–phonon interaction by NiO modification. The Poisson’s ratio shows values less than 0.3 for the modified samples, indicating a high cross-linked density for this glass system. The reduction in σ at the last concentration of NiO (x = 10 mol%) might mean that more doping 10 mol% NiO might cause loosely packed atoms in glass system [51, 52],

Table 1 The experimental values of ultrasonic based constants, longitudinal modulus (L), shear modulus (G), Young’s modulus (E), bulk modulus (K), Poisson’s ratio (σ) and microhardness (H)
Full size table
Fig. 3
figure 3

The variation of longitudinal (L), shear (G), Young’s (E) and bulk (K) moduli for studied glass samples

Full size image

4.3 FTIR spectra

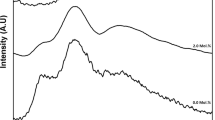
Structural vibrational units in the glass system network were examined using FTIR measurement. The undoped glass, as shown in Fig. 4, reveals several absorption bands extending from the beginning of the measurements at 400 up to 2000 cm−1. The leading prominent and characteristic absorption bands are usually observed at 630, 700, 900, 1050, 1320 and 1460 cm−1. However, the band positions, along with band assignments, are listed in Table 2.

Fig. 4
figure 4

FTIR absorption spectra for glass systems

Full size image
Table 2 Band assignments for the bands present in FTIR spectra for studied glasses
Full size table

On adding NiO to the host glass, the intensity of this band decreased as NiO may be changing the bond strength and length. Also, at the same time, Modifier oxides NiO added to the borate glass network can alter the number of BO4 and BO3 units by generating NBOs. A minor shift followed this in some bands of BO4 groups toward higher wave numbers. Two bands appeared in the mid-IR region at around 950 cm−1 and 1350 cm−1, respectively, assigned to BO4 and BO3 units. The shift in bands could indicate structural changes in the borate network. The increment in NiO content at the expense of B2O3 might be transforming some of the BO3 triangles to BO4 tetrahedra or vice versa. We used a deconvolution method to confirm these assumptions to estimate the fraction of BO4 units in the borate network. The Peak Fit program (version 4.12) was employed for this purpose.

Figure 5 a representative example of deconvolution was performed on the spectra of a (NiO 10) glass sample. On adding NiO, the band intensity of BO3 units decreased, accompanied by increasing band intensity of BO4 units. Table 3 represents the analysis results for 0 and 10 mol% NiO glass samples. The observed bands were attributed to asymmetric stretching vibrational modes of orthoborate, pyroborate, and triangle BO3 group. The deconvolution analysis helped quantify the fraction of NiO-doped BO4 units in the borate network. The study suggests that introducing NiO in varying concentrations influences the borate network's structure, leading to observable changes in the FT-IR spectra. Table 3 also shows the relation between nickel oxide concentration and N4 content, indicating that Increasing nickel oxide levels increase N4 in glass. On the other hand, N3 decreases with nickel oxide content. In addition, nickel oxide level has a significant impact on NBOs. As a result of the negative charge on NBOs, electrons are quickly excited at longer wavelengths [53,54,55,56,57,58]. As a result of the above arguments, the N4 ratio plays the most significant role in increasing density and reducing molar volume.

Fig. 5
figure 5

Example for the Gaussian deconvoluated curves of NiO 10 (fit goodness parameter R2 0.99)

Full size image
Table 3 De-convolution parameter of the infrared spectra of studied glasses (C) is the band center and (A) is the relative area (%) of the component band, N4 and N3
Full size table

4.4 UV–Vis spectra

Figure 6a depicts the change in optical reflectance R(λ) spectra of the non-doped and NiO-doped samples in the wavelength range from 200 to 2000 nm. One can be realized that the absence of interference fringes. Moreover, the reflectance values are affected by both the wavelength and the NiO concentrations. This increases after the incorporation of NiO and then gradually decreases with increasing NiO contents. The reduction in reflectance with increasing the concentration of NiO is attributed to the increase in the scattering of photons via the rise in surface morphology roughness. Also, the increase in free transporter absorption of photons can be attributed to the decrease in the optical reflectance due to high carrier concentrations, which leads to increasing the IR scattering and decreasing the reflectance [59, 60].

Fig. 6
figure 6

a Reflectance, R as a function of wavelength, λ, b refractive index, n as a function of wavelength, λ, and c variation of the optical conductivity (σopt) with wavelength (λ) of studied glass samples

Full size image

The refractive index is an important material property due to its relationship to electronic polarization and material fields. Figure 6b depicts the refractive index for the non-doped and NiO-doped samples. It is noted that all samples show the same characteristics. Moreover, the refractive index changes with the increase in wavelength, such as a normal dispersion behavior of the undoped and doped NiO samples. In addition, the refractive index rises after the pure sample is doped to 2 mol% NiO, and then gradually decreases with enhancing NiO contents from 4 to 10 mol%.

Consequently, this refractive index change confirms the difference in the optical properties of borate glasses with NiO doping. The increase in refractive index with the introduction of 2% NiO indicates that this sample is suitable for improving the performance of optoelectronic devices such as photodetectors. Figure 6c reveals the change in optical conductivity concerning wavelength for the undoped and doped-NiO samples. It is shown that there is an increase in optical conductivity after the base sample 0% NiO was doped by two mol% NiO and gradually decreases with enhancing contents of NiO from 4 to 10 mol%. This indicates that a two mol% NiO doped sample is more suitable for optoelectronic applications.

4.5 Dielectric study

From Fig. 7a, which shows the relation between (n2 − 1)−1 and (hν)2, values of Eo and Ed have been computed for studied glass samples, as seen in Table 4. It was obtained that Ed values increased after 2 mol% NiO doped in the undoped sample, then gradually decreased with enhancing NiO contents from 4 to 10 mol%. This decrease is attributed to the modification in chemical bond number, type, and bonding energy caused by introducing NiO ions in the host lattice. Otherwise, the Eo values decrease in the sample that doped by two mol% NiO while gradually boosting with increasing NiO concentration from 4 to 10 mol%. It is found that ε∞ increased after the undoped sample was doped to 2 mol% NiO, then gradually decreased with enhancing NiO ions' content from 4 to 10 mol%. This change may be due to the change in the amorphicity of samples. In addition, we also noted that values of εL > ε∞ for all samples confirm the coexistence of free carriers. Therefore, from Fig. 7b, εl and N/m* were determined for the undoped and doped samples (Table 4). According to Eq. (14), the plasma resonance frequency (Wp) values were extracted of undoped and doped-NiO samples, the values of εl, N/m*, and Wp increased after the undoped sample was doped by 2 mol% NiO, decreasing with enhancing NiO ions contents from 4 to 10 mol%. These changes result from the variation in bond length with different concentrations of NiO ions. In addition, from the relation between (n2 − 1)−1 and λ−2 of samples at a longer wavelength as shown in Fig. 7c, values of n∞ and λo have been obtained, then values of So based on Eq. 16, (listed in Table 5), it is found that values of λo and So decrease for the sample was doped by two mol% NiO ions, then gradually increased with enhancing concentrations of NiO from 4 to 10 mol%. Studying nonlinear optical parameters is paramount in the area of optoelectronic applications. Figure 8a, b depicts the variation of X(1) and X(3) as a function of wavelength (λ) of the undoped and NiO doped samples, respectively. One can see values of X(1) and X(3) increase for the sample was doped by two mol% NiO, then gradually decreased with raising contents of NiO ions from 4 to 10 mol%. 2 mol% NiO ions doped, then gradually increase with enhancing concentrations of NiO from 4 to 10 mol%. Furthermore, Fig. 8c illustrates the variation in the nonlinear refractive index (n2) with wavelength for the undoped and NiO-doped samples. It is detected that values of n2 follow the same behavior as X(3). The maximum values of X(3) and n2 were observed for the sample doped with 2 mol% NiO ions, specifically at ~ 792 nm, with values of 3.1 × 10–17 esu and 1.07 × 10–5, respectively. These results suggest that the sample doped with 2 mol% NiO is an excellent candidate for nonlinear optical applications and is more suitable for optoelectronic devices than other samples.

Fig. 7
figure 7

a The relation between (n2 − 1)−1 and (hν)2, b variation of real dielectric constant (εr), as a function of wavelength (λ2), and c the relation between (n2 − 1)−1 and (λ)−2 for studied glass samples

Full size image
Table 4 Values of the optical parameters no, ε∞, Ed, Eo, εl, and N/m* of studied glass samples
Full size table
Table 5 Values of the optical parameters Wp, n∞, λo, and So of studied glass samples
Full size table
Fig. 8
figure 8

a Linear optical susceptibility (X(1)) as a function of wavelength (λ), b nonlinear optical susceptibility (X(3)) as a function of wavelength (λ), and c nonlinear refractive index (n2) as a function of wavelength (λ) of studied glass samples

Full size image

4.6 Physical properties

The density (ρ) and molar volume (Vm) of NiO-doped B2O3–K2O–PbO glasses are listed in Table 6 and Fig. 9. The ρ of the undoped glass sample recorded 3.355 g/cm3 and with NiO content increase; a slight decrease in the density is presented and followed by a continuous rise from 3.189 to 3.556 gm/cm3. On the one hand, the first decrease with a glass sample containing two mol% of NiO at the cost of B2O3 might be attributed to the reduction in boron atoms in the glass network, which reduces the boron-to-oxygen ratio. On the other hand, the increase is due to the gradual rise in the NiO, which has a higher density of 6.67 g/cm3 compared to B2O3, which has a density of 2.46 g/cm3. However, it is due to the increment in the glass sample's molar mass caused by replacing the borate 69.6 g/mol molecular weight with NiO of 74.7 g/mol, which is heavier in molecular weight. With further increases in NiO content, the BO4 starts to assemble around the Ni [61]. The variation of both ρ  and Vm are represented in Fig. 9. The reduction in Vm is accountable for the increase in glass densities and the takeover of NiO with lower molecular volume (11.2 cm3/mol) on B2O3 (28.3 cm3/mol). The addition of NiO contracts the glass network with a reduction inVm, and it might reflect in the reduction of the non-bridging oxygens (NBOs) [61].

Table 6 The values of density (ρ), molecular weight (VM), average boron–boron separation ‹dB–B›, Ni+ ion concentration (N), polaron radius (rp) and internuclear distance (ri)
Full size table
Fig. 9
figure 9

Variation of sample density and molar volume of glass samples with NiO concentration

Full size image

The data show that the <dB–B> reveals a decreasing value, which contrasts with all sample's compactness caused by the reduction in Vm and the increment in density values the obtained values are tabulated in Table 5. For the same reason, the values of both rp and ri calculated by Ni ion concentration (N) reveal a continuous decrease with NiO content increase. This reduction trend secures the shortened bond length with stronger bonds in this glass network.

4.7 Shielding parameters

Figure 10a presents μm plot with hυ in a wide range μm was affected by two main factors: the incoming radiation energy and NiO and B2O3 concentrations in the composite. Regarding the first factor, a decay curve was recorded. The maximum μm values recorded at 0.015 MeV (see Table 7) and equal to 48.13, 48.73, 49.42, 50.59, and 51.08 cm2/g for NiO 0 to NiO10, respectively, demonstrating that they retained high values at low energies. This decreased behavior was pronounced till energy of about 1 MeV; from 1 to 5 MeV, a constant behavior was recorded, and then a little increase was observed up to 10 MeV. From this, it was concluded that an increase in the energy of the incoming photons led to a decrease in the μm values of the structure. This trend is reflected in the effectiveness of this glass as a radiation shield material against low-energy photons, with a decrease in performance when exposed to radiation of higher energy. Focusing on the element’s concentrations, the NiO 10 sample had the greatest μm values at all energies, followed by Ni8, and so on, with Ni0 having the smallest μm values. The Ni10 glass, which had the highest NiO concentration, also has the highest μm values. Therefore, increasing the amount of NiO in the structure resulted in more interactions between the incoming photons and the atoms of constituents of the glass, thus more photons were absorbed or scattered by the glass being attenuated from penetrating through the material. Figure 10b shows the theoretical values of µL versus hυ. Initially, a rapid decrease with an increase in hυ was observed. Then, a gradual reduction up to 9 MeV was observed owing to the cross section of Compton scattering relative to E−1. At high γ-energies E > 9 MeV, the pair production process dominates and is proportional to log E.

Fig. 10
figure 10

Influence of photon energy on a μm, b (μL), c HVL of studied glass samples using Phy/X software

Full size image
Table 7 The comparison between the calculated values using PHITS code and Phy/X software of the mass attenuation coefficient for studied glass samples
Full size table

The plots for the HVL and MFP, representative of 0.015–15 MeV incident hυ (Figs. 10c and 11, respectively), revealed that the low γ-energy zone is characterized through MFP minimum values, which gradually increase as the γ-energy increases result from the photoelectric interaction, which at the lowest energy is dominant. A Compton interaction dominates up to 9 MeV, while MFP increases with episode energy. Finally, pair production dominates at E > 10 MeV in the zone of highest photon energy. The previous Figures showed that the Ni-10 sample exhibited the best shielding characteristics among all prepared samples, as it had the highest µm and µL while recording the lowest HVL and MFP. However, the NiO-0 sample showed the lowest μm and µL and the highest HVL and MFP at photon compared with the others. They listed the values of µm that were calculated theoretically using the Phy/X software and PHITS code at different photon energies.

Fig. 11
figure 11

The theoretical values of the mean free path (MFP) of studied glass samples versus the photon energy (hυ)

Full size image

For showing the shielding effectiveness of the material under study, (Zeff) is used. Figure 12 exhibits the Zeff changes through the photon energy for the B2O3–K2O–PbO–NiO glass structure within the (0.015–15) MeV energy domain. Zeff values were in the range of 21.05–38.89 for (NiO 0), 21.36–58.00, for (NiO 2), 21.66–57.14, for (NiO 4), 22.27–55.55, for (NiO 8) and 22.59–54.83 for (NiO 10) samples (see Table 8). Zeff values are most significant at energies below 0.1 MeV. The peaks at 0.1 MeV occurred on Pb's K-absorption edge. Zeff values rapidly decreased during the photoelectric effect dominance region between 0.1 and 1 MeV. After 3 MeV, Zeff values increase due to the Z2-dependent cross section of pair formation. Zeff showed a maximum for (NiO 10 over NiO 0) at 15 MeV after properly increasing Ni concentration. The lowest values of Zeff were between 1 and 3 MeV. Consequently, there is a linear dependence in Z with the increase in Zeff in high-energy regions due to the dominance of Compton scattering [62,63,64].

Fig. 12
figure 12

The theoretical values of the effective atomic number (Zeff) of studied glass samples versus the photon energy (hυ)

Full size image
Table 8 The comparison between the calculated values of the effective atomic number (Zeff) for studied glass samples
Full size table

5 Conclusions

This study shows that NiO doping significantly affects the optical, mechanical, and shielding properties of B2O3–K2O–PbO glasses. From the outcome of our investigation it is possible to conclude that:

  • The highest values of longitudinal, shear, and Young's moduli were observed for the sample with 10 mol% NiO content, while the bulk modulus reached its maximum at 8 mol%.

  • The optical properties of the samples also showed significant changes after NiO doping, with an increase in optical reflectance, refractive index, and optical conductivity for the 2 mol% NiO doped sample, followed by a gradual decrease with increasing NiO content

  • Additionally, the results indicated that NiO doping managed to an increase in glass density, a decrease in molar volume, and a decrease in the average boron–boron internuclear distance, which suggested a strengthening of the borate glass network

Finally, the shielding properties of the samples were evaluated, and it was found that Ni 10 demonstrated the best shielding characteristics among all the prepared samples, with the highest mass &linear attenuation coefficients. These findings suggest that NiO doped B2O3–K2O–PbO glasses may have potential applications in radiation shielding and other technological fields that require materials with improved mechanical and optical properties.

Besides, the radiation shielding investigations displayed increased µm and decreased HVL values with further NiO additives. The improved shielding characteristics paved the ways toward the applicability of these glasses for radiation shielding purposes. Additional, in future work, we will prepare the same glass system with higher contents of NiO and lower B2O3 aiming to obtain glass samples with higher transparency as well as better radiation shielding parameters.