Exploring the rich solution landscape of the generalized Kawahara equation: insights from analytical techniques

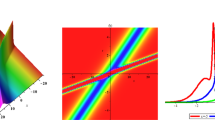
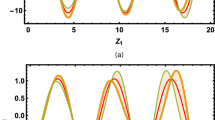
Abstract

The primary objective of this investigation revolves around scrutinizing the generalized Kawahara equation, a consequential nonlinear evolution equation prevalent in diverse physical domains such as shallow water waves, ion-acoustic waves within plasmas, and nonlinear acoustics. This equation manifests intricate dynamical attributes, notably featuring the emergence of solitary waves, shock waves, and chaotic solutions. In our pursuit to elucidate the nuanced behavior inherent in the generalized Kawahara equation, we deploy two robust analytical methodologies: the Khater II method and the variational iteration method. These methodologies offer adept and precise avenues for approximating solutions to nonlinear partial differential equations. Through our analytical scrutiny, a diverse spectrum of solutions comes to light, encompassing solitary wave solutions, periodic solutions, and chaotic solutions. Our exploration delves into the impact wielded by diverse parameters on solution behaviors, thereby furnishing invaluable insights into the foundational physical mechanisms at play. The findings derived from our inquiry contribute significantly to comprehending the intricate dynamics of the generalized Kawahara equation, concurrently establishing connections with other nonlinear evolution equations. This study augments the existing reservoir of knowledge concerning nonlinear wave phenomena and sets the stage for further investigations into the convoluted behaviors exhibited by these intricate systems.

Appendix

Here, we explain the headlines of the employed schemes in our paper. The major steps of the Khater II method and He’s variational iteration method are given to show more details of both computational and numerical techniques.

1.1 Analytical scheme

Assume the following form for the equation of nonlinear evolution:

$$\begin{aligned} \mathcal {E}(\mathfrak {U},\,\mathfrak {U}_{x},\,\mathfrak {U}_{t},\,\mathfrak {U}_{x,\,t},\ldots )=0, \end{aligned}$$

(18)

where $\mathcal {E}=\mathcal {E}(x,t)$ is a polynomial of $\mathfrak {U}(x,t)$ and its partial derivatives, wherein the highest-order derivatives and nonlinear terms are concerned. The main steps of the employed method are as follows:

Step 1. The traveling wave transformation

$$\begin{aligned} \mathfrak {U}(x,\, t)=\nu (\mathfrak {T}), \quad \mathfrak {T}=x+c\,t, \end{aligned}$$

(19)

converting Equation (18) into the following ODE

$$\begin{aligned} \mathcal {E}\left( \nu ,\, \nu ^{\prime }, \nu ^{\prime \prime },\, \ldots \right) =0, \end{aligned}$$

(20)

where $\mathcal {E}$ is a polynomial in $\nu (\mathfrak {T})$ and its total derivatives, wherein $\nu ^{\prime }(\mathfrak {T})=\frac{d \nu }{d \mathfrak {T}}$.

Step 2. We suppose the solution of (20) is of the form

$$\begin{aligned} \nu (\mathfrak {T})= \sum \limits _{i=1}^n \left( a_i f(\mathfrak {T} )^i+b_i \phi (\mathfrak {T} ) f(\mathfrak {T} )^{i-1}\right) +a_0, \end{aligned}$$

(21)

where $a_i\,(i=0,1,2,3, \ldots ,N),\, b_i\,(i=0,1,2,3, \ldots ,N)$ are arbitrary constants to be determined, such that $a_{-n}\ne 0$ or $a_{n} \ne 0$, and $\phi (\mathfrak {T} ),\, f(\mathfrak {T} )$ is an unidentified function to be determined afterward. This function satisfies the following equation:

$$\begin{aligned} f'(\mathfrak {T})\rightarrow -\beta -f(\mathfrak {T} )^2,\phi '(\mathfrak {T} )\rightarrow -f(\mathfrak {T} ) \phi (\mathfrak {T} ), \end{aligned}$$

(22)

where $\beta$ is arbitrary constant.

Step 3. The positive integer N in equation (21) is determined by considering the homogeneous balance between the highest-order derivatives and the highest-order nonlinear terms present in equation (20).

Step 4. We calculate the necessary derivatives, such as $\nu ^\prime$, $\nu ^{\prime \prime }$, and so on, and substitute equation (21) along with the derivatives into equation (20), taking into account the functions $\phi (\mathfrak {T})$, $f(\mathfrak {T})$. This substitution results in a polynomial in terms of $\phi (\mathfrak {T})$, $f(\mathfrak {T})$ and its derivatives. We then equate all the coefficients of this polynomial to zero. This process leads to a system of equations that can be solved to determine the values of $a_k$ and the functions $\phi (\mathfrak {T})$ and $f(\mathfrak {T})$.

1.2 Approximate scheme

     Presented below is a general nonlinear differential equation that exemplifies the fundamental concept of He’s variational iteration method:

$$\begin{aligned} \mathfrak {T}\, \mathcal {K}(x,t)+\Upsilon \, \mathcal {K}(x,t)=\eta (x,t), \end{aligned}$$

(23)

where $\mathfrak {T}$ represents a linear operator, $\Upsilon$ denotes a nonlinear operator, and $\eta (x,t)$ represents a known analytical function. According to the variational method, a correction functional can be formulated as follows:

$$\begin{aligned} \mathcal {K}_{\varrho +1}(x,t)=\mathcal {K}_{\varrho }(x,t)+\int _{0}^{t} \upsilon \, \left( L \mathcal {K}_{\varrho }(x,\, \mathfrak {T})+N \tilde{\mathcal {K}}_{\varrho }(x,\, \mathfrak {T})-\eta (x,\, \mathfrak {T})\right) d \mathfrak {T}. \end{aligned}$$

(24)

In this scenario, $\upsilon$ corresponds to a general Lagrange multiplier that can be determined optimally through variational theory, while $\tilde{\mathcal {K}}{\varrho }$ signifies a restricted variation, namely $\varsigma , \tilde{\mathcal {K}}{\varrho }=0$. The stationary conditions can be expressed as follows:

$$\begin{aligned} \left\{ \begin{array}{c} 1+\upsilon =0, \\ \\ \upsilon ^{\prime }=0.~~~~~ \end{array} \right. \end{aligned}$$

(25)

This in turn gives

$$\begin{aligned} \upsilon =-1. \end{aligned}$$

(26)

Applying He’s variational iteration technique to the $\mathbb{M}\mathbb{K}$ model enables the investigation of its approximate solution, resulting in the determination of the analytical and numerical values as well as the absolute difference between these two values (absolute error).