Reshaping of breathing pulses to action potential profile propagating in an electromechanical coupled model for biomembranes and nerves

Abstract

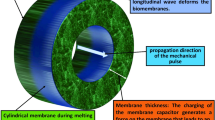
The problem of understanding the neurons function and thereby the brain has been the nexus of research during the last decades, in the fields of medicine and physical neuroscience. In the existing experimental studies, it is shown that the nerve impulse is an electromechanical signal which forces the membrane through the transition while propagating. In this work, we study localized nonlinear excitations in an electromechanical coupled model for biomembranes and nerves. We thus report on the presence of envelope solitons of the nerve impulse in this electromechanical coupled model. More importantly, we reshaped the obtained envelope solitons (breathing pulses) to action potential profile from direct numerical simulation of the coupled model. The numerical results shows a clear concordance with the analytical predictions. The theoretical results obtained in this work shows that the nerve impulse propagating through the proposed model is an electromechanical impulse that propagates along the nerve using spatial and temporal dimensions in the form of localized propagating nonlinear waves as predicted by experimental studies existing in the literature.

Appendices

Appendix A

The following are expressions of parameters used in Eq. (3):

$$\begin{aligned} {a_1}&= \dfrac{{\sqrt{{H_1}} \left( {V_1^3{g_{Ca}} - 3V_1^2{V_{Ca}}{g_{Ca}} + 3{V_1}V_2^2{g_{Ca}} - 6V_2^3{g_L} - 3V_2^3{g_{Ca}} + 3V_2^2{V_{Ca}}{g_{Ca}}} \right) }}{{6{C_m}c_0^2V_2^3}},\,\, \nonumber \\ {a_2}&= \dfrac{{\sqrt{{H_1}} {g_K}{\omega _0}{V_K}}}{{{C_m}c_0^2{V_0}}},\,\, \nonumber \\ {a_3}&= \dfrac{{\sqrt{{H_1}} {g_{Ca}}{V_0}\left( {V_1^2 + {V_1}{V_{Ca}} - 2V_2^2} \right) }}{{4{C_m}c_0^2V_2^3}},\,\,\nonumber \\ {a_4}&= -\dfrac{{\sqrt{{H_1}} {g_K}{\omega _0}}}{{{C_m}c_0^2}},\,\,{a_5} = -\dfrac{{\sqrt{{H_1}} {g_{Ca}}V_0^2\left( {{V_{Ca}} + 3{V_1}} \right) }}{{6{C_m}c_0^2V_2^3}},\nonumber \\ {a_6}&= \dfrac{{\sqrt{{H_1}} \left( {V_1^3{V_{Ca}}{g_{Ca}} -3{V_1}V_2^2{V_{Ca}}{g_{Ca}} + 6V_2^3{V_L}{g_L} +3V_2^3{V_{Ca}}{g_{Ca}} + 6{{\textrm{i}}_{ext}}V_2^3} \right) }}{{6{C_m}c_0^2V_2^3{V_0}}},\nonumber \\ {b_1}&= -\dfrac{{\sqrt{{H_1}} {V_0}\left( {5V_3^4 + 15V_3^2V_4^2 +6{V_3}V_4^3 - 24V_4^4} \right) }}{{144c_0^2{V_4}^5{\omega _0}}},\,\,{b_2} = -\dfrac{{\sqrt{{H_1}} \left( {V_3^2 + 8V_4^2} \right) }}{{24c_0^2{V_4}^2}},\nonumber \\ {b_3}&= \dfrac{{\sqrt{{H_1}} {V_0}^2\left( {10{V_3}^3 +15{V_3}{V_4}^2 + 3{V_4}^3} \right) }}{{144c_0^2{V_4}^5{\omega _0}}},\,\, \nonumber \\ {b_4}&= - \dfrac{{\sqrt{{H_1}} {V_0}{V_3}}}{{42c_0^2{V_4}^2}},\nonumber \\ {b_5}&= -\dfrac{{5\sqrt{{H_1}} {V_0}^3\left( {2{V_3}^2 + {V_4}^2} \right) }}{{48c_0^2{V_4}^5{\omega _0}}},\nonumber \\ {b_6}&= \dfrac{{\sqrt{{H_1}} {V_0}^2}}{{24c_0^2{V_4}^2}},\,\,{b_7} = \dfrac{{\sqrt{{H_1}} \left( {{V_3}^5 + 5{V_3}^3{V_4}^2 +3{V_3}^2{V_4}^3 - 24{V_3}{V_4}^4 + 24{V_4}^5} \right) }}{{144c_0^2{V_4}^5{\omega _0}}},\nonumber \\ q&= \dfrac{{{{\left( {\rho _0^A} \right) }^2} \beta }}{{c_0^2}}, \nonumber \\ p&= \dfrac{{\rho _0^A\alpha }}{{c_0^2}}, \nonumber \\ \mu&= \dfrac{\upsilon }{{\sqrt{{H_1}} }}, \nonumber \\ {\lambda _1}&= \dfrac{{{H_2}}}{{{H_1}}}c_0^2, \nonumber \\ \sigma&= \dfrac{{{C_m}V_0^2{H_1}}}{{2{\tau _2} {{\left( {\rho _0^A} \right) }^2}c_0^4}} \end{aligned}$$

(33)

$$\begin{aligned} {\sigma _1}&= \dfrac{{\sqrt{{H_1}} }}{{{\tau _1}c_0^2}}, \nonumber \\ {\eta _0}&= a_2^2{b_7} - {a_2}{a_6}{b_2} + {a_2}{b_2}{\sigma _1}, \nonumber \\ {\eta _1}&= a_2^2{b_1} - {a_1}{a_2}{b_2} + 2{a_2}{a_4}{b_7} - {a_2}{a_6}{b_4} - {a_4}{a_6}{b_2} + \left( {{a_2}{b_2} + {a_2}{b_4} + {a_4}{b_2}} \right) {\sigma _1}, \nonumber \\ {\eta _2}&= \left( {{a_2}{b_3} - {a_1}{b_4} - {a_3}{b_2} + 2{a_4}{b_1} - {a_6}{b_6}} \right) {a_2} + \left( {{a_4}{b_7} - {a_6}{b_4} - {a_1}{b_2}} \right) {a_4} + \left( {{a_2}{b_4} + {a_2}{b_6} + {a_4}{b_2} + {a_4}{b_4}} \right) {\sigma _1},\nonumber \\ {\eta _3}&= \left( {{a_2}{b_5} - {a_3}{b_4} + 2{a_4}{b_3} - {a_5}{b_2} - {a_1}{b_6}} \right) {a_2} + \left( {{a_4}{b_1} - {a_3}{b_2} - {a_6}{b_6} + {b_6} - {a_1}{b_4}} \right) {a_4} + \left( {{a_4}{b_4} + {a_4}{b_6} + {a_2}{b_6}} \right) {\sigma _1},\nonumber \\ {\kappa _0}&= - {a_2}{b_2}{\sigma _1},\,\,{\kappa _1} = - {\sigma _1}\left( {{a_2}{b_2} + {a_2}{b_4} + {a_4}{b_2}} \right) ,\,\,{\kappa _2} = - {\sigma _1}\left( {{a_2}{b_4} + {a_2}{b_6} + {a_4}{b_2} + {a_4}{b_4}} \right) , \nonumber \\ {\beta _0}&= {C_m}{a_2}{b_2} + {a_1}{a_2} - {a_2}{\sigma _1} - {a_4}{a_6} + {a_4}{\sigma _1},\,\,{\beta _1} = {C_m}\left( {{a_2}{b_4} + {a_4}{b_2}} \right) + 2{a_2}{a_3}, \nonumber \\ {\beta _2}&= {C_m}\left( {{a_2}{b_6} + {a_4}{b_4}} \right) + 3{a_2}{a_5} + {a_3}{a_4},\,\,{\beta _4} = {\sigma _1}\left( {{a_2} -{a_4}} \right) , \nonumber \\ {\gamma _0}&= - D{a_2}{b_2},\,\,{\gamma _1} = - D \left( {{a_2}{b_4} + {a_4}{b_2}} \right) ,\,\,{\gamma _2} =- D\left( {{a_2}{b_6} + {a_4}{b_4}} \right) , \nonumber \\ {\delta _1}&= {C_m}{a_4}, \nonumber \\ {\delta _2}&= {C_m}{a_2}, \nonumber \\ {\delta _3}&= - D{a_4}, \nonumber \\ {\delta _4}&= D{a_2}, \nonumber \\ {\delta _5}&= {\sigma _1}\left( {{a_2} + {a_4}} \right) , \nonumber \\ {\delta _6}&= {\sigma _1}{a_4},\,\,{\delta _7} = {a_2}{\sigma _1}. \end{aligned}$$

(34)

Appendix B

$$\begin{aligned} {P_1}&= \dfrac{{v_g^2{\delta _2} - {\gamma _0}}}{{{\delta _2} \omega }},\nonumber \\ {P_2}&= \dfrac{{{c_g}^2({k^2}{\lambda _1} + 1) + 4k \omega {\lambda _1}{c_g} - 6{k^2} + {\omega ^2}{\lambda _1} - 1}}{{\left( {{k^2}{\lambda _1} + 1} \right) \omega }}, \nonumber \\ {Q_{{1_r}}}&= \dfrac{{ - {k^4}{\gamma _1}^2 + {k^2} \left( {9{\delta _3}{\omega ^2}{\beta _1} + 9{\delta _1} {\omega ^2}{\gamma _1} - 9{\gamma _2}{\eta _1} + 11{\eta _2}{\gamma _1}} \right) + 9{\eta _3}{\eta _1} - 12{\delta _1}^2{\omega ^4} - {\omega ^2}{\beta _1}^2 - 10{\eta _2}^2 + 21{\delta _1}{\omega ^2}{\eta _2}}}{{6{\eta _1}{\delta _2}\omega }},\nonumber \\ {Q_{{1_i}}}&= - \dfrac{{{k^4}{\delta _3}{\gamma _1} + 4{\omega ^2}{k^2}{\delta _1}{\delta _3} - {k^2}{\delta _3}{\eta _2} - {\omega ^2}{\beta _1}{\delta _1} - {\beta _1}{\eta _2} + {\beta _2}{\eta _1}}}{{2{\eta _1}{\delta _2}}},\nonumber \\ {Q_1}&= {Q_{{1_r}}} + i{Q_{{1_i}}}, \nonumber \\ {R_1}&= \dfrac{{{k^2}{\delta _4} - {\beta _0}}}{{2{\delta _2}\omega }}, \nonumber \\ {K_{{1_r}}}&= \dfrac{1}{2}\dfrac{{{\kappa _0}}}{{{\delta _2}\omega }}, \nonumber \\ {Q_2}&= \dfrac{{{p^2}\left( {{k^2}{\lambda _1} + 1} \right) - 6q {k^2}\left( {1 - \lambda _1} \right) }}{{12\left( {1 - \lambda _1} \right) \left( {{k^2}\lambda _1 + 1} \right) \omega }}, \nonumber \\ {R_2}&= \dfrac{{\mu {k^2}}}{{2({k^2}\lambda _1 + 1)}}, \nonumber \\ {K_2}&= \dfrac{{{\sigma }}}{{2\left( {{k^2}\lambda _1 + 1} \right) \omega }}, \nonumber \\ {K_{{1_i}}}&= - \frac{{{\delta _7}}}{{2{\delta _2}}}, \nonumber \\ {K_1}&= {K_{{1_i}}} + i{K_{{1_i}}}, \nonumber \\ {M_1}&= - \dfrac{{{\omega ^2}{\beta _4}^2 - {\omega ^2}{\beta _4}{\delta _5} + {\omega ^2}{\delta _5}^2 + {\kappa _1}^2}}{{3{\eta _1}{\delta _2}\omega }}, \nonumber \\ {N_{{1_r}}}&= \dfrac{{6{k^2}{\omega ^2}{\beta _4}{\delta _3} + 3{k^2}{\omega ^2}{\delta _3}{\delta _5} + 2{k^2}{\gamma _1}{\kappa _1} - 2{\omega ^2}{\beta _1}{\beta _4} + {\omega ^2}{\beta _1}{\delta _5} - 3{\omega ^2}{\delta _1}{\kappa _1} + 3{\eta _1}{\kappa _2} - 5{\eta _2}{\kappa _1}}}{{3{\eta _1}{\delta _2}\omega }}, \nonumber \\ {N_{{1_i}}}&= \dfrac{{4{k^2}{\beta _4}{\gamma _1} + 3{k^2}{\delta _3}{\kappa _1} - 2{k^2}{\delta _5}{\gamma _1} - 6{\omega ^2}{\beta _4}{\delta _1} + 3{\omega ^2}{\delta _1}{\delta _5} + {\beta _1}{\kappa _1} - 4{\beta _4}{\eta _2} + 5{\delta _5}{\eta _2} - 3{\delta _6}{\eta _1}}}{{3{\eta _1}{\delta _2}}}, \nonumber \\ {N_1}&= {N_{{1_r}}} + i{N_{{1_i}}}, \nonumber \\ {\Gamma _r}&= \dfrac{{6\left( {{\beta _4}{\delta _5} - {\delta _5}^2} \right) \left( {{\lambda _1} - 1} \right) {k^2}{\omega ^2} + \left( {6\lambda _1{\kappa _1}^2 + p \lambda _1{\eta _1}{\kappa _1} + 6{\kappa _1}^2} \right) {k^2} - p {\eta _1}{\kappa _1}}}{{12{\eta _1} \left( { 1 - \lambda _1} \right) {k^2}{\delta _2}\omega }},\nonumber \\ {\Gamma _i}&= \dfrac{{6\lambda _1\left( {{\beta _4} - 2{\delta _5}} \right) {\kappa _1}{k^2} - \left( {\left( {{\beta _4} - 2{\delta _5}} \right) \left( {p {\eta _1}\lambda _1 + 6{\kappa _1}} \right) } \right) {k^2} - p {\eta _1}\left( {{\beta _4} - 2{\delta _5}} \right) }}{{12{\eta _1}\left( { 1 - \lambda _1} \right) {k^2}{\delta _2}}}, \nonumber \\ {\Gamma }&= {\Gamma _r} + {\Gamma _i}, \nonumber \\ {\chi _r}&= \dfrac{{3\left( {{\delta _5} - {\beta _4}} \right) {\delta _3}{k^2}{\omega ^2} + \left( {{\beta _1}{\beta _4} - 2{\beta _1}{\delta _5} - 3{\delta _1}{\kappa _1}} \right) {\omega ^2} + 2{k^2}{\gamma _1}{\kappa _1} - 5{\eta _2}{\kappa _1}}}{{6{\eta _1}{\delta _2}\omega }}, \nonumber \\ {\chi _i}&= \dfrac{{ - \left( {{\beta _4}{\gamma _1} + 3{\delta _3}{\kappa _1}} \right) {k^2} + 3{\omega ^2}\left( {{\beta _4} - {\delta _5}} \right) {\delta _1} + 2{\beta _1}{\kappa _1} + 4{\beta _4}{\eta _2} - 5{\delta _5}{\eta _2} + 3{\delta _6}{\eta _1}}}{{6{\eta _1}{\delta _2}}}, \nonumber \\ {\chi }&= {\chi _r} + {\chi _i} \end{aligned}$$

(35)