1 Introduction

In the past few decades, the emergence of distinct nontrivial bursting dynamics has been explored in numerous models [1,2,3,4,5,6]. In particular, the electrophysiology activities, bifurcation structures, and important computational effects of neurons are discussed in detail (See. [1, 2] and the references therein). The detailed review of discrete bifurcation mechanisms and their intrinsic relation with various forms of neuronal dynamics were reported in Ref. [3]. The occurrence of different forms of spiking trains, periodic and chaotic bursting oscillations, mixed-mode oscillations, and their transitions were explored in detail with the numerical and experimental studies [4,5,6]. The general characteristic feature of bursting dynamics is the recurrent appearance of active phases of continuous action potential interspersed by quiescence states. The Seminal theoretical work of Rinzel [7] encouraged the researchers to uncover various complex neuronal dynamics. There exist ample numbers of bursting patterns in different nonlinear dynamical systems, that have been illustrated in the literature via different dynamical processes, namely double Hopf bifurcation with slow-varying parametric excitations [8], saddle-node bifurcation via asymmetric and pitchfork or fold bifurcation through symmetric bursting oscillation [9], the coexistence of multiple bursting dynamics in a modified van der Pol-Duffing system [10], various compound bursting using slow-fast analysis [11], and to name a few. In recent years, the complex electrical activity of distinct neuronal dynamics was explored using multiple time-scale systems elaborated in different disciplines [12,13,14,15,16]. The detailed stability analysis and bifurcation structures of discrete bursting dynamics, ranging from simple slow-fast dynamical systems to complex models with various applications, have been explored using a multiple time-scale approach [12]. Advantages of converting the existing slow-fast variable in a parametrically and externally excited system into a single slow variable to uncover the complicated bifurcation structures of mixed-mode oscillations presented in a Duffing and van der Pol oscillator [13]. The emergence of different clusters of compound bursting and multi-frequency bursting oscillations has been found in different classes of multi-scale systems [15, 16].

Recently, a special type of bursting dynamics in the multiple time-scale system, known as amplitude-modulated bursting (AMB), has garnered significant interest in the research community. Indeed, the regular busting oscillation exhibits the alternate appearance of firing and rest states. However, in the case of amplitude-modulation bursting dynamics, there exist distinct envelopes in the active phase of busting (firing state) followed by the rest states.

Vo et al. [17] ascertain the emergence of amplitude-modulated bursting while illustrating the dynamical process of intracellular calcium dynamics. Later, Han et al. explored the appearance of AMB dynamics in distinct model systems using time-dependent slow parametric modulation [14]. The simplest chemical reaction model with multi-frequency slow-parametric excitations is capable of exhibiting AMB dynamics [18]. Further, the amplitude-modulation in spiking dynamics has been identified in a Butera model [19], a modified form of coupled conductance-based biophysical model [20], and three coupled forced LCR oscillator with common sharing nonlinear element [21].

In most of the earlier reports which elucidate the appearance of AMB dynamics owing to torus canard dynamics [19,20,21,22,23]. On the other hand, Han et al. reported that AMB can also appear due to multi-frequency slow parametric modulation process [14], and they used a specific modulation term \(\lambda = \alpha + A_1 \cos (\omega _1 t)+A_2 \cos (\omega _2 t)\), which contains a combination of control parameter \(\alpha\) and two slow parametric excitations. Similarly, in the chemical reaction system multiple frequency forcing plays a key role in the formation of AMB dynamics [18]. Noteworthy, in the aforesaid reports [14, 18], authors used multiple-frequency forcing as a time-varying parameter to obtain the AMB. It is well known that time-varying parameter-based models provide more insight into exploring various complex dynamical patterns. However, the experimental realization of time-varying parameters in a real-time electronics experiment is still challenging task. To conquer such difficulties, in this study, we have used only a slow parametric or multiple-frequency forcing as an external excitation in the Liénard system to elucidate the AMB dynamics in both numerical and experiment realizations. Additionally, to the best of the authors’ knowledge, the experimental observation of AMB dynamics has not yet been reported.

The rest of this paper is organized as follows: Sect. 2 explains the details of the model system and its distinct stability with the response of system parameters. The appearance of different patterns of amplitude-modulated busting and its emerging mechanism is explored in Sect. 3. The real-time electronic experimental results of AMB are delineated in Sect. 4. The emergence of distinct complex patterns of AMB dynamics is presented in Sect.  5. In the final section, we presented the overall summary of our results.

2 Multi-frequency excited Liénard system

In order to illustrate the distinct formation of amplitude-modulated bursting oscillations, we have considered a paradigmatic model of the Liénard system which manifests a rich variety of complex dynamics such as spiking trains, bursting and mixed-mode oscillations, extreme events, and critical transient dynamics, to name a few [4, 9, 24,25,26]. This choice of model enables us to delve into the intricate behavior of the system and explore its amplitude-modulated bursting oscillations in a comprehensive manner. In this study, our focus is on a multi-frequency excited Liénard system, described by the following set of differential equations:

$$\begin{aligned} {\dot{x}}= & {} y \nonumber \\ {\dot{y}}= & {} -\alpha xy-\beta x^3-\gamma x +A_1 \sin (\omega _1 t)+A_2 \sin (\omega _2 t). \end{aligned}$$
(1)

Here, the parameters \(\alpha ,~\beta ,~\gamma\) represent the nonlinear damping coefficient, strength of nonlinearity, and natural frequency of the system, respectively. \(A_1\), \(A_2\), and \(\omega _1\), \(\omega _2\) are the amplitudes and frequencies of external periodic forcing. In the context of this study, we maintain fixed values for various system parameters, namely \(\alpha\), \(\beta\), \(\gamma\), \(A_1\), \(A_2\), and \(\omega _1\), while systematically altering the external forcing frequency \(\omega _2\). Within this parameter space, the system exhibits discrete bursting oscillations, which include the intriguing dynamics of amplitude-modulated bursting. Further elaboration on these dynamics will be provided in the forthcoming section.

Fig. 1
figure 1

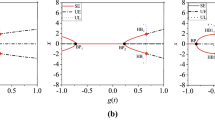
Stability bifurcation diagram in the \((\delta -x)\) plane of Eq. (1) for fixed system parameters \(\alpha = 0.02\), \(\beta =0.5\), and \(\gamma = -0.5\). Red, green, and blue circles signify the stable focus (SF), unstable focus (UF), and saddle (Sd) equilibrium points, respectively. Closed Magenta circles denote limit points (LP1 and LP2)

Full size image
Fig. 2
figure 2

Stability phase diagram in the \((\delta - \alpha )\) plane: the existence of distinct stability a for (1, 0) and (−1, 0) fixed points of the system. Different stability regions, namely stable focus (SF), unstable focus (UF), stable node (SN), unstable node (UN), and saddle (Sd), are presented as red, green, magenta, cyan, and blue colors, respectively

Full size image

2.1 Stability analysis

We begin to analyze the system by finding its stability (Eq. 1). For the fixed system parameters value of \(\alpha = 0.02\), \(\beta =0.5\), and \(\gamma = -0.5\), the model system exhibits three different equilibria such as stable focus at (1,0), saddle at (0, 0), and unstable focus at (−1, 0). We have depicted the stability bifurcation of the system in Fig. 1, while considering various amplitudes of the external forcing. To comprehensively explore the potential stability configurations within the system, we aggregate the amplitudes of the two external forces into a single parameter denoted as \(\delta\). This approach enables us to investigate the full spectrum of stability states present in the system. We have used the continuation software XPPAUT AUTO [27] to calculate the distinct stability of the system. In the S-shaped bifurcation plot of Fig. 1, the stable focus (SF), unstable focus (UF), and saddle (Sd) equilibriums are illustrated as red, green, and blue circles, respectively. The system exchanges its stability at the limit points LP1 and LP2 which are depicted by the magenta color points.

Significantly, the nonlinear damping parameter \(\alpha\) in the Liénard system plays a vital role in shaping the distinctive patterns of amplitude-modulated bursting dynamics. Consequently, we have presented a stability phase diagram within the \(\delta\) versus \(\alpha\) plane, focusing on the fixed points (1, 0) and (−1, 0), as confirmed in Fig. 2a and b. This phase diagram reveals various stability regions, denoted by colors such as red for stable focus (SF), green for unstable focus (UF), magenta for stable node (SN), cyan for unstable node (UN), and blue for saddle (Sd), as depicted in Fig. 2a and b. Furthermore, when considering the (0, 0) fixed point, the system consistently demonstrates a saddle equilibrium across a wide range of \(\delta\) and nonlinear damping parameter values.

Fig. 3
figure 3

Amplitude-modulated bursting dynamics of Multi-frequency excited Liénard system: time series of x(t) signify a regular bursting for \(\omega _2\) = 0.001, b two-envelope AMB for \(\omega _2\) = 0.002, three-envelope AMB for \(\omega _2\) = 0.003, four-envelope AMB for \(\omega _2\) = 0.004, five-envelope AMB for \(\omega _2\) = 0.005, and six-envelope AMB for \(\omega _2\) = 0.006, respectively. Blue lines in the upper panel of a–f denote combined external periodic excitations (\(f_1(t)+f_2(t)\)) represent slowly varying forcing frequency in the system. Cyan color in the temporal evolutions in a denotes no modulation and b–f represent the appearance of distinct modulation in the firing states

Full size image
Fig. 4
figure 4

a Transformed phase portrait in the (\(\delta - x\)) plane for a \(\omega _2 = 0.001\) and c \(\omega _2 = 0.002\). SF, UF, and Sd denote stable focus, and unstable focus saddle equilibria of the system. At the critical value of \(\delta\), the system changes its stability represented by limit points (LP1) and (LP2). Stability bifurcation (S-shaped curve) is superimposed with the front view transformed phase portraits revealing the dynamical evaluation of bursting oscillation (b) and amplitude-modulation dynamics (d). Bifurcation delay signifies as a term \(\tau\)

Full size image

3 Amplitude-modulated bursting oscillations

To elucidate the various forms of amplitude-modulated bursting dynamics in the slowly varying, multi-frequency excited Liénard system, we employed numerical solutions of the model equations. These equations were solved using the fourth-order Runge–Kutta (RK4) method with a step size of 0.01 and we have taken the initial conditions (\(x_0, y_0\)) as (\(0.5, -0.5\)). The transient dynamics have been removed wherever necessary. The results obtained were then visualized as a series of temporal plots, presented in Fig. 3a–f. During the investigation, we kept the system parameters fixed at \(\alpha = 0.02\), \(\beta = 0.5\), \(\gamma = -0.5\), \(A_1 = 0.1\), \(A_2 = 0.2\), \(\omega _1 = 0.001\), while allowing \(\omega _2\) to vary within the range of (0.001, 0.006). Within this parameter space, the Liénard system exhibited diverse patterns of amplitude-modulated bursting dynamics.

For \(\omega _2 = 0.001\) (Fig. 3a), the system displayed regular bursting dynamics characterized by the alternation between resting and firing states. Notably, in this case, there was no modulation evident in the firing states. This absence of modulation was confirmed by plotting the combination of the two external forcing terms, \(A_1 \sin (\omega _1 t) + A_2 \sin (\omega _2 t)\), in the upper panel of Fig. 3a. As we gradually increased the value of \(\omega _2\) to 0.002, the system began to exhibit amplitude-modulated bursting (cf. Fig. 3b). In this scenario, modulation became apparent in the action potentials of the firing states, and this modulation was reflected as the presence of two distinct frequencies within each oscillation period, as shown in the upper panel of Fig. 3b. Continuing to vary the control parameter \(\omega _2\) from 0.003 to 0.006, the system demonstrated AMB with three, four, five, and six distinct envelopes in the firing states, as depicted in Fig. 3c–f, respectively. The combined external forcing terms, plotted in the upper panels of Fig. 3c–f, clearly illustrated the number of envelopes emerging in the AMB dynamics, which depended on the slowly varying frequency of the external forcing term.

3.1 Evolution of amplitude-modulated bursting

This subsection elucidates the mechanism underlying the emergence of amplitude-modulated bursting in the slowly varying, multi-frequency excited Liénard system. We have generated the stability bifurcation diagram of the system, which has been overlaid with transformed phase portraits depicting regular bursting oscillations in the \(\delta\) versus x plane, as illustrated in Fig. 4a. In this figure, the cyan color indicates the absence of modulation in the active states of bursting dynamics. Conversely, the transformed phase portrait representing AMB dynamics, presented in Fig. 4c, clearly signifies the presence of modulation in the firing state of the system.

For a more insightful interpretation of the dynamical evolution, we have exclusively displayed a front view of the transformed phase portrait in Fig. 4b. The firing states begin to appear as the system trajectory approaches the limit point LP1 and persist until the trajectory reaches the subsequent turning point LP2. Notably, as the system approaches LP2, the firing state transitions into the resting state and then moves toward LP1 through the SF region. This dynamic process continually occurs within the model. However, the system eventually reaches a stable state at the point LPi instead of LP2. The time difference (\(\tau\)) between the points LPi and LP2 is known as the bifurcation delay or slow passage effect, which arises during the evolution of bursting oscillation. We have observed a similar dynamical evolution in the system during the formation of two-envelope AMB dynamics, as confirmed in Fig. 4d. However, it is important to note that the bifurcation delay time gradually increases with the influence of the control parameter \(\omega _2\) of the system.

4 Experimental results

In order to validate the numerical observations of AMB dynamics, we conducted an experimental study using an electronic setup. To achieve this, we derived an analog circuit based on model Eq. (1), as illustrated in Fig. 5. The circuit comprises operational amplifiers (UA741), analog device multiplier chips (AD633), resistors (R), capacitors (C), and external sinusoidal waveform generators \(f_1(t)\) and \(f_2(t)\). We obtained the following circuit equations by applying Kirchhoff’s laws at the two nodes of the capacitors \(C_1\) and \(C_2\):

Fig. 5
figure 5

Circuit Analog circuit diagram of the Liénard system with a pair of external periodic forcing

Full size image
Fig. 6
figure 6

a Electronics experimental setup of Liénard system in the laboratory. Experimental results of distinct bursting dynamics: b regular bursting, c two envelope, and d three envelope of amplitude-modulated bursting, for \(\Omega _2\) = 100 Hz, \(\Omega _2\) = 200 Hz, and \(\Omega _2\) = 300 Hz, respectively

Full size image
$$\begin{aligned}{} & {} -C_1 \left( \frac{dv_1}{dt} \right) = -\frac{0.1v_1v_2}{R_5}+\frac{v_2}{R_6}-\frac{0.01v^3_2}{R_7} +\frac{1}{R_1}((F_1 \textrm{sin} \Omega _1 t)+(F_2 \textrm{sin} \Omega _2 t)) \end{aligned}$$
(2)
$$\begin{aligned}{} & {} -C_2 \left( \frac{dv_2}{dt} \right) = -\frac{v_1}{R_2}. \end{aligned}$$
(3)

After rearranging and merging Eqs. (2) and (3), we obtain following circuit equation.

$$\begin{aligned} C_1C_2R_2R_5\left( \frac{d^2v_2}{dt^2} \right)= & {} 0.1C_2R_2v_2\left( \frac{dv_2}{dt} \right) +\frac{R_5}{R_6}v_2-0.01 \frac{R_5}{R_7}v^3_2 \nonumber \\{} & {} +\frac{R_5}{R_1}(F_1 \textrm{sin} \Omega _1 t)+(F_2 \textrm{sin} \Omega _2 t). \end{aligned}$$
(4)
Fig. 7
figure 7

Temporal dynamics of complex amplitude-modulated bursting in Liénard system for a higher damping value: a regular bursting for \(\omega _2\) = 0.01, b and c emergence of six and three consecutive bursting which is separated by a long rest state for \(\omega _2\) = 0.011 and 0.112. d Intricate dynamics of two and three-envelope AMB appearing in between bursting oscillations for \(\omega _2\) = 0.013. e Alternate manifestation of two-envelope AMB and bursting oscillations for \(\omega _2\) = 0.014. f Recurrent two-envelope AMB for \(\omega _2\) = 0.015

Full size image

To experimentally observe the AMB as observed in the numerical study, we carefully selected the circuit parameters, such as resistors and capacitors in Eq. (4). To facilitate parameter comparison, we rescaled the parameters as follows: \(t \rightarrow \tau = R_1C_1t\), and \(x_1 = v_1\), \(x_2=v_2\), \(\alpha =0.1 \frac{R_1}{R_5}\), \(\beta =0.01 \frac{R_1}{R_7}\), and \(\gamma = \frac{R_1}{R_6}\). When we fix the circuit parameter value \(R_1\) = \(R_2\) = \(R_3\) = \(R_4\) = 10 \(\mathrm {K\Omega }\), \(R_5\) = 49.87 \(\mathrm {K\Omega }\), \(R_6\) = 19.96 \(\mathrm {K\Omega }\), \(R_7\) = 220 \(\mathrm {\Omega }\), \(C_1\) = \(C_2\) = 10 \(\textrm{nF}\), \(F_1\) = 0.110 V, \(F_2\) = 0.120 V, \(\Omega _1\) = 100 Hz, and gradually varying \(\Omega _2 \in\) (100–300 Hz), the Liénard circuit manifests different patterns of amplitude-modulated bursting. The obtained results from the experiment are presented in Fig. 6. The experimental setup for a multi-frequency excited Liénard circuit is depicted in Fig. 6a. At \(\Omega _2\) = 100 Hz, the system displays bursting dynamics, characterized by alternating periods of firing and rest, as illustrated in Fig. 6b. Furthermore, when we vary the forcing frequency \(\Omega _2\) to 200 Hz, the system exhibits two envelopes of amplitude-modulation dynamics, as shown in Fig. 6c. Upon further variation of \(\Omega _2\) to 300 Hz, the Liénard circuit demonstrates three envelopes of AMB, as demonstrated in Fig. 6d. It is evident from Figs. 6c and d that during the active state of the action potential, the Liénard circuit exhibits distinct modulation in response to the slowly varying forcing frequency of the circuit.

5 Complex amplitude-modulated bursting oscillations

Furthermore, we have identified distinct complex amplitude-modulated bursting in the Liénard system, specifically for a higher value of damping, \(\alpha\) = 0.45, while keeping other parameters fixed at \(\beta = 0.5\), \(\gamma = -0.5\), \(A_1\) = 0.1, \(A_2\) = 0.2, and \(\omega _1\) = 0.01. For fine-tuning, we varied \(\omega _2\) within the range (0.01, 0.015). The observed results are depicted in Fig. 7. Indeed, we obtain the transition from regular bursting oscillation (for \(\omega _2\) = 0.01: Fig. 7a) to two-envelope AMB (for \(\omega _2\) = 0.015: Fig. 7f), however, in-between the system exhibits more complex bursting dynamics, along with alternating periods of bursting and AMB dynamics. The temporal evolution of six consecutive bursting oscillations, marked by extended rest states that occur when \(\omega _2\) = 0.011, is illustrated in Fig. 7b. Similarly, for \(\omega _2\) = 0.012, the system displays three successive bursting dynamics separated by long rest states (cf. Fig. 7c). When we increase \(\omega _2\) to 0.013, the system exhibits even more complex dynamics, with alternating appearances of two and three-envelope AMB dynamics occurring intermittently with the bursting oscillations, as shown in Fig. 7d. Furthermore, as we vary the control parameter to \(\omega _2\) = 0.014, the two-envelope AMB and three consecutive bursting dynamics recurrently appear in the system, as depicted in Fig. 7e. Finally, we observe two-envelope AMB dynamics for \(\omega _2\) = 0.015, as shown in Fig. 7f. It is noteworthy that the dynamical analysis of complex AMB dynamics follows a similar mechanism as discussed in Sect. 3.1. Hence, we have omitted its discussion here to avoid repetition.

6 Conclusion

In summary, we have introduced the phenomenon of amplitude modulation bursting (AMB) within a multi-frequency stimulated Liénard system. This system exhibits a diverse range of complex bursting oscillation patterns and distinctive AMB envelopes, influenced by both nonlinear damping parameters and external forcing frequencies. The discrete envelopes of AMB dynamics emerge as a consequence of the slowly varying multi-frequency excitation applied to the Liénard system. Importantly, our experimental findings closely align with the results obtained from numerical simulations.